Исследование коэффициентов взаимного влияния в двухполяризационных антенных решетках

Антенные решетки (АР) находят широкое применение в различных областях радиотехники, например в радио- и телекоммуникациях, системах радиолокации, спутниковых системах связи, беспроводных сетях, радиотелескопах и др. Одной из важных характеристик антенной решетки является ее диаграмма направленности (ДН). Параметры и форма ДН АР могут оказывать существенное влияние на характеристики разрабатываемых радиосистем [1]. Так, например, для повышения пропускной способности MIMO-систем связи увеличивают число используемых поляризаций и уменьшают расстояние между антенными элементами решетки, однако при этом начинает проявляться их взаимное влияние [2]. Считается, что в результате этого диаграмма направленности изолированного антенного элемента будет отличаться от ДН того же элемента в составе антенной решетки (парциальной диаграммы направленности) [3]. Причем связь между этими диаграммами направленности описывается с помощью матриц

взаимного влияния С [4]. Существует несколько подходов для их определения, например расчет с помощью матриц импеданса (Z-матрица) или матриц рассеяния (S-матрица) [5–7] либо расчет на основе анализа парциальных диаграмм направленности и диаграмм направленности изолированного антенного элемента [4].

Оценку матриц импеданса, матриц рассеяния, а также парциальных ДН обычно производят по результатам численного электродинамического моделирования. В случае большого числа антенных элементов такое моделирование требует значительного времени, а оптимизация AP потребует проведения большого числа симуляций.

Таким образом, целью работы являлось исследование взаимного влияния между двухполяризационными антенными элементами (АЭ), входящими в состав линейной антенной решетки. Предложена модель взаимного влияния АЭ, позволяющая оценить матрицу С и прогнозировать искажения ДН по результатам моделирования изолированного элемента и двухэлементной АР.

LH^^e © Бажанова О.В. и др., 2023

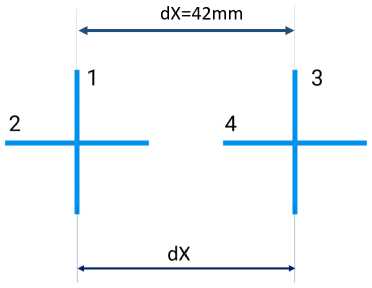
Рис. 1. Антенная решетка, состоящая из двух кросс-дипольных элементов с вертикальной и горизонтальной поляризациями (цифрами указана нумерация портов)

Fig. 1. Antenna array consisting of two cross-dipole elements with vertical and horizontal polarization (numbers indicate port numbering)

1.    Исследование взаимного влияния двухполяризационных элементов антенной решетки

Для анализа взаимного влияния в среде электродинамического моделирования была построена модель антенной решетки, состоящей из двух кросс-диполей, поляризации которых были ориентированы горизонтально и вертикально (рис. 1). Длина одного диполя была равна половине рабочей длины волны.

В результате моделирования были получены диаграммы направленности изолированных элементов и элементов в составе решетки (парциальные) (рис. 2), соответствующие каждому из четырех портов (в обозначениях рис. 1). Под диаграммой направленности изолированного элемента понимается диаграмма одного антенного элемента в отсутствие других элементов решетки, и она обозначается F iis ) ( 9 , ф ), где i = 1, 2, ..., N ( N - число портов, в данном случае равно четырем). Парциальной диаграммой направленности (обозначим как F jp ) ( 9 , ф ), где j = 1, 2, ..., N ) называют ДН элемента, находящегося в составе антенной решетки при условии, что остальные антенные элементы этой же решетки нагружены на 50 Ом.

Видно, что указанные диаграммы отличаются как по форме, так и параметрам: ширине главного лепестка и максимуму коэффициента усиления. В работе [8] говорится о том, что искажение парциальной ДН за счет взаимного влияния элементов в антенной решетке связано с рассеянием электромагнитных волн ближнего поля на соседних АЭ. При этом результирующая парциальная ДН любого из АЭ может быть представлена в виде суперпозиции изолированных ДН элементов

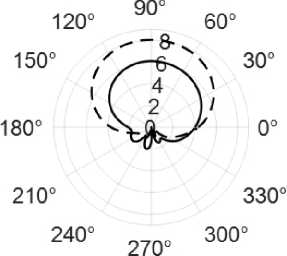
Рис. 2. Диаграммы направленности в горизонтальной плоскости изолированного антенного элемента (пунктирная линия) и элемента в составе решетки (сплошная линия)

Fig. 2. Radiation patterns in the horizontal plane of an isolated antenna element (dashed line) and an element in the array (solid line)

(расположенных в координатах АР). Тогда связь между этими диаграммами можно записать следующим образом:

F p ' ° ' ^ F is 'М ,                   (1)

i = 1

где C ij e С - коэффициенты взаимного влияния. Здесь через Q_v обозначен v - й набор угловых координат ( 9,ф ), что позволило представить комбинации всех значений углов в виде одномерного массива. В рассматриваемом случае 9 1 = 0 °,..., 9   = 180 ° и ф = 0 °,..., ф   = 359 ° , тогда раз-

181                 1            360

мер массива Q_v составляет 181 х 360 элементов.

Таким образом, можно сказать, что физический смысл коэффициентов взаимного влияния c_ij заключается в том, что они характеризуют амплитуду и фазу поля, переизлучаемого i -м антенным элементом АР, если запитывается только j -й элемент.

В матричной форме коэффициенты взаимного влияния, парциальные и изолированные ДН име- ют вид:

' Fis'(°,) F '(°1' ■ ■ FNs '(°1'' F (is' = F1's ^) F2(is'(°2 '   ■ ■ FNs '(°2' : . ^ '(° M ) F2(is'(° M ' ■ F (is        ) FN (°M 'J ' F1( p '(°1' F2P '(°1' - • FNp '(°1'" F (p' = Fp '(°, ' F2(p'(°2 ' - • FNp '(°2 ' v F1( p'(° M ' Fip'(° M ' - • FNp'(° m 'v c 11

^C 1 м

C = v CN1  '- CNM у

Таблица 1. Вычисленные значения для расстояния между АЭ, равного 0,5 длины волны Table 1. Calculated values for a distance between AEs equal to 0,5 wavelengths

С mn	1	2	3	4
1	1 , 041 + e 0079 j	- 0 , 013 - e 0 , 008 j	- 0 , 248 - e 0 , 240 j	- 0 , 001 - e 0 , 017 j
2	0 , 012 + e 0 , 003 j	1 , 021 - e 0 , 008 j	- 0 , 042 - e 0 , 013 j	- 0 , 130 + e 0 , 077 j
3	- 0 , 205 - e 0 , 251 j	0 , 036 - e 0 , 010 j	1 , 033 + e 0 , 101 j	- 0 , 007 + e 0 , 013 j
4	- 0 , 0299 - e 0 , 017 j	- 0 , 128 + e 0 , 075 j	0 , 008 + e 0 , 007 j	1 , 022 - e 0 , 008 j

Таблица 2. Результаты расчета

Table 2. Calculation results

c mn	1	3	c mn	2	4
1	1 , 041 + e 0 , 078 j	- 0 , 248 - e 0 , 2398 j	2	1 , 020 - e 0 , 009 j	- 0 , 130 + e 0 , 077 j
3	- 0 , 204 - e 0 , 251 j	1 , 033 + e 0 , 099 j	4	- 0 , 128 + e 0 , 074 j	1 , 022 - e 0 , 009 j

Тогда (1) приобретает следующий вид:

F ⁽ is ) C = F ⁽ p ) , (2)

где С – матрица взаимного влияния.

Для определения матрицы С необходимо умножить обе части выражения (2) на матрицу, обратную F ⁽ is ) . В общем случае можно применять операцию псевдообращения, так как она дает возможность получения приближенного решения с минимальной среднеквадратичной ошибкой в случае, когда строгое решение невозможно [7]. Тогда

C = ( F ⁽ is ) ^ F ⁽ p ) , (3) где символ «+» обозначает псевдообратную матрицу Мура – Пенроуза.

Для исследуемой решетки, показанной на рис. 1, был проведен анализ значений элементов матрицы взаимного влияния. Пример вычисленных значений для расстояния между АЭ равного 0,5 длины волны, представлен в табл. 1.

Как видно из табл. 1, элементы C12, С21, С14, С41, С23, С32, С34, С43 значительно меньше остальных элементов матрицы. Вероятно, это объясняется тем, что указанные элементы выражают связь между АЭ, работающими в разной (причем ортогональной) поляризации. В исследуемой конфигурации АР такие АЭ практически не оказывают влияния друг на друга. Для проверки этого предположения были рассчитаны матрицы взаимной связи в отдельности для двух антенных решеток, каждая из которых состояла из двух антенных элементов одинаковой поляризации: два вертикальных диполя и два горизонтальных. Результа- ты расчета представлены в табл. 2. Для удобства сравнения нумерация портов была сохранена. Как видно, элементы матриц взаимного влияния, рассчитанные для однополяризационных решеток, практически совпали с соответствующими им элементами матрицы для двухполяризационной решетки, что подтвердило предположение о пренебрежимо малом взаимодействии антенных элементов, работающих в разной поляризации.

Далее в работе было проведено исследование взаимного влияния АЭ в зависимости от расстояния между ними ( dX ). Оно варьировалось от половины до полутора рабочих длин волн. Для каждого значения расстояния вычислялась матрица взаимного влияния. Графики зависимостей элементов матрицы С , представленные на рис. 3, подтверждают, что с увеличением расстояния между АЭ решетки приводит к значительному уменьшению взаимного влияния. В дальнейшем эти зависимости понадобятся для верификации результатов расчетов с применением предложенной модели.

2.    Модель взаимного влияния антенных элементов в составе антенной решетки

В работе [9] авторы рассматривают взаимное влияние АЭ в АР следующим образом: антенные элементы, окружающие активный элемент, на который подается мощность, поглощают часть излученной им мощности и затем переизлучают ее, таким образом служа вторичными источниками электромагнитных волн. Тогда поле, формируемое этим активным элементом антенной решетки, является суперпозицией полей всех излучателей

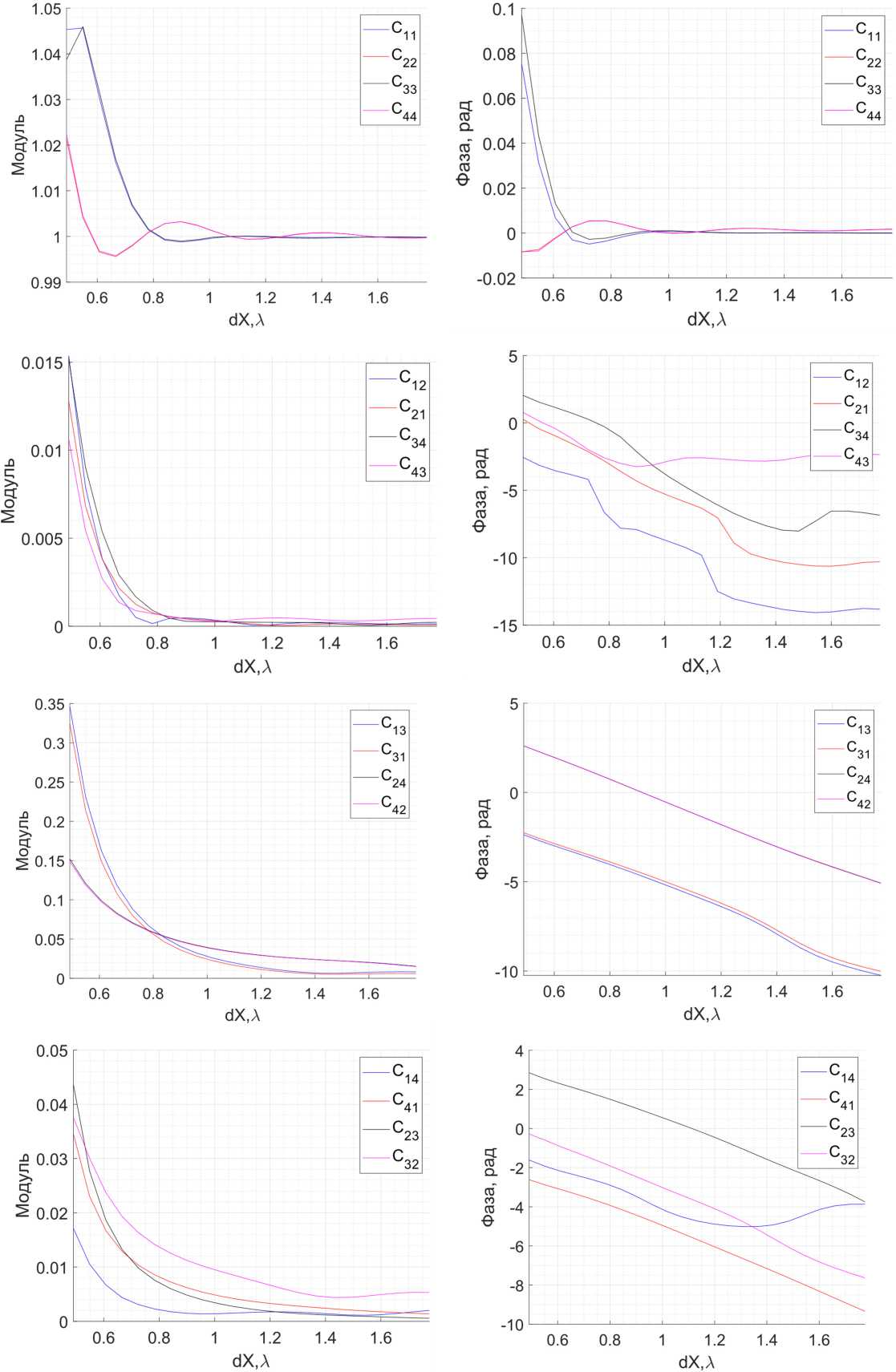
Рис. 3. Графики зависимостей элементов матрицы С от расстояния между АЭ решетки

Fig. 3. Graphs of the dependences of matrix elements C on the distance between the array AEs

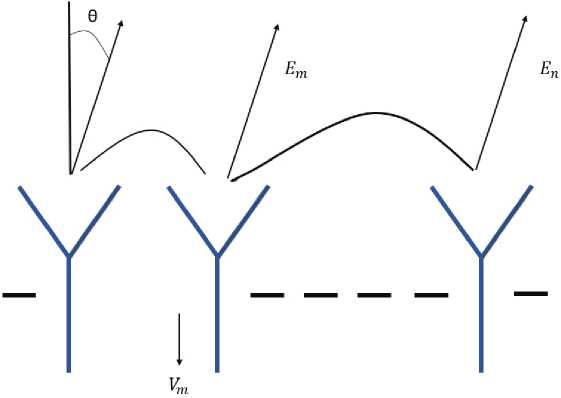
Рис. 4. К модели взаимного влияния антенных элементов в составе линейной антенной решетки

Fig. 4. To the model of mutual influence of antenna elements in a linear antenna array

с учетом переизлученной ими мощности, что проиллюстрировано на рис. 4.

Рассмотрим применение этого подхода на примере антенной решетки, изображенной на рис. 1. Взаимодействие можно представить как бесконечную последовательность процессов излучения, поглощения и дальнейшего переизлучения мощности антенными элементами рассматриваемой решетки.

В данной работе предложено каждый антенный элемент решетки рассматривать как изолированный, то есть с неискаженной диаграммой направленности. Тогда, если все АЭ в решетке одинаковые, предложенный подход позволяет провести электродинамическое моделирование только один раз для одного элемента. Это значительно уменьшает расчетную сложность задачи. Тогда парциальную диаграмму направленности после первого переизлучения мощности портом 3 можно записать следующим образом: F is ) + qF 3 is ) , где q – коэффициент, учитывающий коэффициент усиления первой антенны в направлении третьей и условия распространения электромагнитной волны, а также зависящий от расстояния между антенными элементами. После второго переизлу-чения части энергии, излученной портом 3, итоговая парциальная диаграмма направленности порта 1 примет вид F ^ is ) + q ² F ^ is ) + qF 3 is ) . И так далее, давая выражение

F 1^P ) = F ^ is ) ( 1 + q ² + • ) + F 3 is ) ( q + q ³ + • ). (5)

Однако ранее было показано, что взаимное влияние элементов, работающих в ортогональных поляризациях, практически отсутствует. В связи с этим сначала рассмотрим взаимное влияние пор- тов 1 и 3. Пусть мощность подается на порт 1, тогда его парциальную диаграмму в соответствии с (1) можно представить в виде

F 1 p ) = c 11 F is ) + c 31 F e is ) ,                                 (6)

где коэффициенты взаимного влияния ( С ₁₁ и С ₃₁ ) характеризуют долю излученной мощности каждым элементом с учетом их взаимодействия.

Сравнивая (5) и (6), получаем:

c и = ¹ + q ² +•••>                                            ⁽⁷⁾

c 13 = q + q ³ + • .                                      (8)

Так как | q | < 1, оба коэффициента представляют собой суммы всех членов убывающих геометрических прогрессий. Тогда:

c 11 ® c 33 ®      -;                                         (9)

• 1    — q 2

• ^c 13 ~ c 31 ~     т .                                     ⁽¹⁰⁾

• 1    - q ²

Для нахождения q в работе использовалась полученная на этапе моделирования зависимость ^ 13 ( r ) (рис. 3). Исходя из формулы (10), расчет q производился путем минимизации среднего отклонения

q ^{( r} )

^{1 -} q ^{2 ( r} )

C 13 ^{( r} )

по всем значениям r . Благодаря предположению об идентичности антенных элементов решетки для уменьшения погрешности вместо C 13 ( г ) использовалось среднее арифметическое

C 13 ^{( r ) +} C 31 ^{( r} ) .

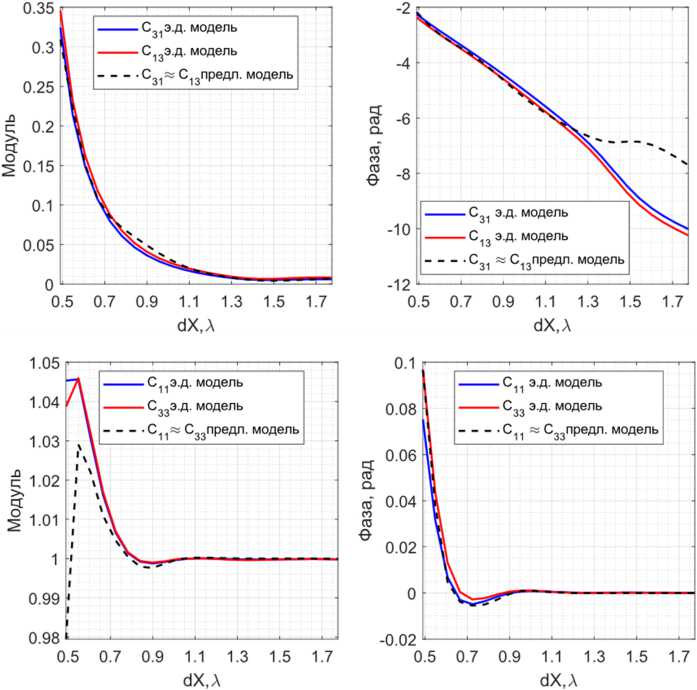
Рис. 5. Зависимости коэффициентов C ₁₁ , C ₁₃ , C ₃₁ и C ₃₃ , рассчитанных с помощью предложенной модели и полученных в результате электродинамического моделирования, от расстояния между элементами

Fig. 5. Dependences of the coefficients C ₁₁ , C ₁₃ , C ₃₁ , and C ₃₃ , calculated using the proposed model and obtained as a result of electrodynamic modeling, on the distance between the elements

Проверка правильности рассчитанных значений q производилась подстановкой их в формулу (9) и сравнением с зависимостью, полученной для коэффициентов Сц ( r ) « С з ₃ ( r ) при электродинамическом моделировании (рис. 3). На рис. 5 приведены зависимости коэффициентов C ₁₁ , C ₁₃ , C ₃₁ , и C ₃₃ от расстояния между элементами, рассчитанные по приведенной модели и полученные в электродинамическом моделировании.

Заметим, что на этом этапе последовательность применения формул (9) и (10) не имеет значения.

Аналогично для портов 2 и 4:

C24 ≈C42 ≈       ;

24    42

C22 ≈C44 ≈       .

1 - q ²

Стоит отметить, что значения q для этих портов отличаются от полученных для портов 1 и 3. Рассчитанные зависимости для коэффициентов C ₂₂ , C ₂₄ , C ₄₂ , и C ₄₄ и результаты электродинамического моделирования отражены на рис. 6.

Приведенные на рис. 5 и 6 зависимости показывают хорошее совпадение, что говорит о возможности применения предложенной модели и метода расчета коэффициентов взаимного влияния

Расчет матрицы взаимного влияния антенной решетки с большим числом элементов может быть выполнен итеративно. Для этого, зная аппроксимацию коэффициента q от расстояния, следует учитывать комбинации переотражений от соседних антенных элементов.

Заключение

В работе проведено исследование взаимного влияния антенных элементов двухполяризационной антенной решетки. Показано, что взаимодействие между элементами, работающими в ортогональных поляризациях, практически отсутствует, а коэффициенты взаимного влияния убывают с увеличением расстояния между антенными элементами. Это позволило разработать модель, основанную на представлении антенной решетки в виде изолированных элементов, взаимодейству-

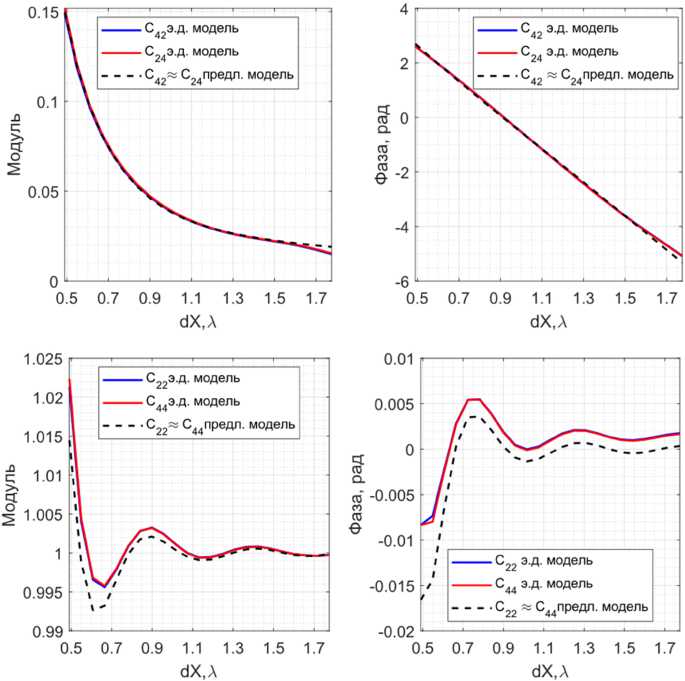
Рис. 6. Зависимости модуля и фазы коэффициентов C ₂₂ , C ₂₄ , C ₄₂ и C ₄₄ , рассчитанных с помощью предложенной модели и полученных в результате электродинамического моделирования, от расстояния между АР в решетке

Fig. 6. Dependences ofthe modulus and phase ofthe coefficients C ₂₂ , C ₂₄ , C ₄₂ , and C ₄₄ , calculated using the proposed model and obtained as a result of electrodynamic modeling, on the distance between the ARs in the lattice

ющих друг с другом посредством поглощения и переизлучения мощности соседними элементами.

Предложенный подход дал возможность аппроксимировать матрицы взаимного влияния элементов антенных решеток, состоящих из большого числа элементов. Для оценки парциальных диаграмм направленности реализуются следующие этапы: электродинамическое моделирование для определения характеристик изолированного АЭ, а также моделирование решетки, состоящей из двух АЭ; расчет матрицы взаимного влияния для смоделированной двухэлементной антенны; оценка коэффициентов, учитывающих условия распространения электромагнитной волны от одного АЭ к другому и переизлучения; расчет ма- трицы взаимного влияния антенной решетки заданного размера.

Результаты работы могут быть использованы при разработке многоэлементных антенных решеток для систем радиосвязи и радиолокации.

Финансирование

Исследование выполнено за счет гранта Российского научного фонда № 21-19-00323,

Для выполнения численных расчетов в работе использовалось оборудование учебно-научного дизайн-центра проектирования радиоэлектронных систем СВЧ, терагерцового и оптического диапазонов на отечественной электронной компонентной базе ФГБОУ ВО «ВГУ».