Исследование локальных напряжений в средней зоне стальной балки, предварительно напряженной вытяжкой стенки, при действии сосредоточенной силы

В настоящее время проведены обширные экспериментальные исследования и разработаны практические рекомендации по расчету обычных балок, работающих на сосредоточенные нагрузки, приложенные к верхнему и нижнему поясным листам конструкций. Вместе с тем следует отметить, что изучению влияния локальных напряжений на работу балок, предварительно напряженных без затяжек, в частности балок, предварительное напряжение в которых создается продольной вытяжкой стенки, посвящено незначительное количество исследований. На ликвидацию указанного пробела направлена настоящая работа.

Рассматривая случай, когда точка приложения сосредоточенной силы P к стенке предварительно напряженной балки находится в середине пролета балки (рис. 1), нужно иметь в виду, что предварительные нормальные напряжения σ , действующие по всей высоте стенки, будут оказывать существенное влияние на распределение поля локальных напряжений и в целом на напряженное состояние стенки в данном сечении.

Существует несколько методов для определения действительных схемы разрушения прямоугольных шарнирно опертых пластинок от произвольно приложенных сосредоточенных сил. При определении напряжений в балке будем опираться на балочную теорию С.П. Тимошенко [1]. Таким образом, суммируя три составляющие напряженного состояния стенки от действия сосредоточенной силы, приложенной к стенке в середине пролета балки, запишем общее выражение нормальных напряжений в поперечном сечении AD , полученное по классической теории для балок без предварительного напряжения:

3 P f l c I     P P ( у ³   3 у )

I1 У +      +

2 c ³ V 2 п )     2 n c   n c V 2 c ³   10 c ₎

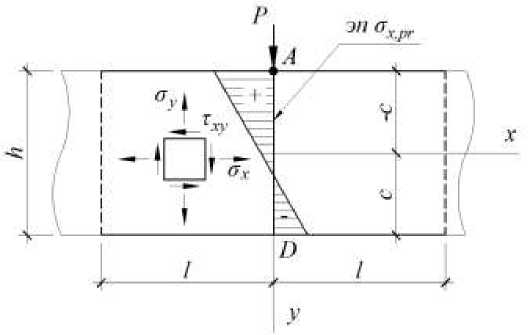
Рисунок 1 - Схема приложения сосредоточенной нагрузки, действующей на стенку в середине пролета предварительно напряженной балки

Так как распределение полей локальных напряжений на достаточном отдалении от точки приложения сосредоточенной силы в середине пролета балки согласно принципу Сен-Венана будет стремиться к нулю, то в этом случае наибольшее влияние на прочность изгибаемого элемента будет оказывать сопротивление стали изгибу Ry , а не срезу Rs . Максимальная сосредоточенная сила P , приложенная в середине пролета балки, из условия прочности эле- мента по изгибающему моменту M :

P max

2 M max l

2 R y W zv l

.

На стадии предварительного напряжения изменение напряжений ^, _рг по коротким сторонам для случая вариации напряжений по верхней кромке стенки относительно оси x , проходящей вдоль середины стенки, запишется:

^ x, pr

—

RK

—----ч I ¹ — 6 • y I .

2 K + 1 )        h

Нужно принять во внимание, что площадь поперечного сечения балки A при толщине стенки t_w = 1 запишется:

A = Aw-

Y w

twh

Y w

Общее выражение нормальных напряжений ное для предварительно напряженных балок:

h

.

Yw gx в поперечном сечении AD, получен-

х

^ = °хо б+ ^ог x       x , o        x , pr

3 ( X   С I      1

—т I  - I У + —

2 c ³ V 2   п J    2 п с

v

2 R y l

^{1 +} y ³

h²   6 K - у . ( K + 1) 2

---

6 у .      ( K + 1)

-

³ y )

-

R y K

2 ( 2 K + 1 )

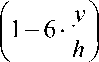
Расстояние от начала координат до верхней и нижней кромок стенки с = h /2, нормальные напряжения будут наибольшими на расстоянии х = 0, согласно принципу Сен-Венана l = h . Используем оптимальные геометрические параметры предварительно напряженной балки двутаврового поперечного сечения K = 1,1754 и yw = 0,496, приведенные в [2], тогда выражения нормаль- ных напряжений в поперечном сечении AD будут равны:

^ х

² R , 6 K - у . ( K + 1) 2 --------------.--------------------------------------------------------

3       У , ( K + 1)

'

V

-       3 K y . ( K + 1)

2 п  4 ( 2 K + 1 ) ( 6 K - у . ( K + 1)² ) J

+

+

f       9 K y . ( K + 1)       - 18 1 y + 4

V 2 ( 2 K + 1 ) ( 6 K - y . ( K + 1)² )   5 п J h п

y ³

h ³

= 2,90 R y

0,099 - 0,783 | y I + 1,273 | y I V h J        V h J

Более детальное исследование распределения напряжений вблизи точки приложения сосредоточенной силы провел Ф. Зеевальд, применив решение Кармана для бесконечно длинной балки. Функция напряжений F ( x , y ) , задающая закон распределения напряжений и кривизны вблизи приложения сосредоточенной силы P , была получена Ф. Зеевальдом и представлена в работе [3].

Ф. Зеевальд разделил напряжение на две составляющие: первая рассчитывается по классической балочной формуле, а другая описывает локальный эффект вблизи точки приложения сосредоточенной силы. Вторую составляющую напряжения можно представить в форме, приведенной в [1]:

P

° х = ^a AD   ,

c

где ао - численный множитель, зависящий от положения точки, в которой определяются локальные напряжения; — - отношение сосредоточенной силы и половины высоты стенки c

балки.

Тогда местные напряжения ^ , возникающие в поперечном сечении стенки предварительно

напряженной балки AD (рис. 1) от действия сосредоточенной силы P при х = 0 :

P

^ х ^{( 0,} У ) = « AD , pr- , _c

² R y 6 K - у , ( K + 1) 2 _х 3       у . ( K + 1)

х

4 . y3 Г      9Ky. (K +1)      -181 y + п h3  V 2(2K +1)(6K - у, (K +1)2) 5п J h

+

f 1 -        3 K y . ( K + 1)

V 2 п  4 ( 2 K + 1 ) ( 6 K - y . ( K + 1)² ) J

P  ² R , 6 K - y . ( K + 1) ²

— ----;

С 3       y . ( K + 1)    ’

^a AD , pr

— _.^           w^          -181У n h3  V2(2K + 1)(бK — Yw(K + 1)2)  5n J h

y

9 K Y w ( K + 1)

— +

+

3 K Y w ( K + 1)

V

2 п  4 ( 2 K + 1 ) ( 6 K - 7„ ( K + 1) 2 ) J_ ^.

Если рассматривать предварительно напряженную балку в сечении AD оптимального поперечного сечения, тогда множители уравнения местных напряжений о будут равны:

« AD , pr ^{( 0}, У ^{) —}

0,099 - 0,783 | У | + 1,273 | У |   ;

V h J       V h J

р

- - 2,90 Ry .                                     (12)

c

Значения множителей a_{AD рг} для определения местных напряжений о в предварительно напряженной балке и множителей a_AD оь для определения местных напряжений о _оЬ в балке без предварительного напряжения представлены в виде графиков на рисунке 2. На расстоянии у — 0 и у — c — h значением местных напряжений о_х можно пренебречь.

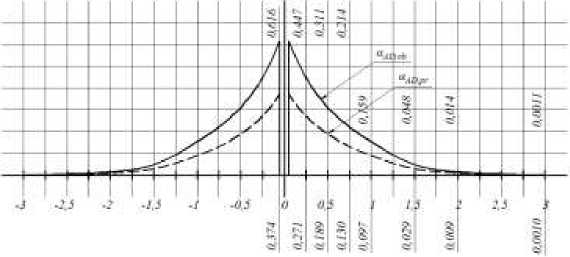
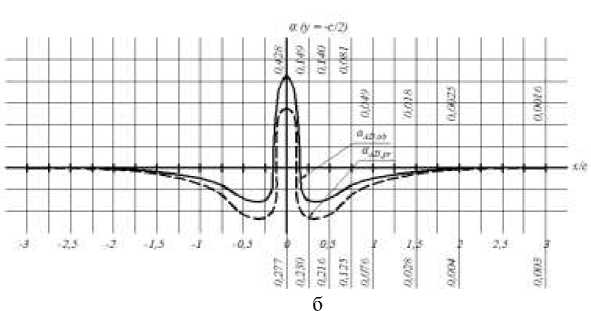
Рисунок 2 - График значений множителя Ою местных напряжений о в сечении AD соответственно для предварительно напряженной балки (пунктир.) и балки без предварительного напряжения (сплош.):

а - при у — — c ; б - при у —

c

— -

.

Таким образом, анализ графика (рис. 2 а) показывает, что сжимающие местные напряжения Т в крайней верхней точке сечения стенки предварительно напряженной балки, при у = — c = — h /2 , в случае действия сосредоточенной силы P будут до 35% меньше сжимающих местных напряжений т_{х оЬ} в стенке балки без предварительного напряжения. Данный результат объясняется тем, что в верхней зоне предварительно напряженной стенки действуют предварительные нормальные растягивающие напряжения, которые, накладываясь на сжимающие местные нормальные напряжения, снижают поле этих напряжений.

Анализ графика (рис. 2 б) показывает, что сжимающие местные напряжения а_х в верхней точке сечения стенки предварительно напряженной балки, при у = — c /2 = — h /4 , в случае действия сосредоточенной силы P будут до 30% меньше сжимающих местных напряжений ст_хоЬ в стенке балки без предварительного напряжения. Однако растягивающие местные напряжения т в этом случае будут до 30% больше растягивающих местных напряжений Т _оЬ в стенке балки без предварительного напряжения. Этот итог объясняется тем, что поле местных напряжений в сечении при у = — h /4 в зоне около точки приложения силы P будет иметь эпюру сжимающих местных напряжений, а по мере отдаления от нее — эпюру растягивающих, и, накладываясь в этом сечении стенки на эпюру предварительных нормальных растягивающих напряжений, в первом случае происходит снижение, а во втором — увеличение местных напряжений о_х . Поскольку в конечном счете амплитуда сжимающих местных напряжений на 17% больше амплитуды растягивающих местных напряжений, то в целом предварительное напряжение в сечении стенки при у = — h /4 оказывает положительное влияние на их распределение по сравнению с обычной балкой.

На рисунке 3 приведены эпюры напряжений о_х в предварительно напряженной балке и в балке без предварительного напряжения при работе от внешней сосредоточенной силы P , приложенной в середине пролета балки, равной соответственно 40 кН .

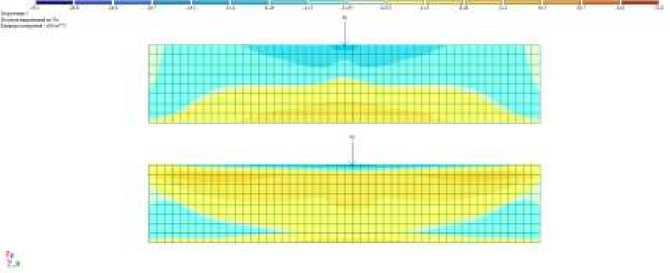
Рисунок 3 — Эпюры нормальных напряжений ох в балке без предварительного напряжения (вверху)

и в предварительно напряженной балке (внизу) при P = 40 кН

Рисунок 4 — Эпюры нормальных напряжений т _1ос по длине балки без предварительного напряжения (слева) и предварительно напряженной балки (справа) при P = 40 кН 65

Для определения степени влияния предварительного напряжения на распределение эпюр локальных нормальных напряжений будем рассматривать их значения в сечении стенки на расстоянии h 4 от верхней кромки стенки в середине пролета балки, где действует наибольший изгибающий момент (рис. 4).

Анализ рисунка 4 показал, что в обычной балке при P = 40 кН напряжения σ будут сжимающими и в 1,5 раза меньшими по модулю, чем в предварительно напряженной балке.