Исследование медленных молекулярных движений в расплавах линейных полимеров

Многие свойства полимеров, находящихся в высокоэлластическом и вязкотекучем состояниях, определяются движениями составляющих их макромолекул. В настоящее время одним из наиболее информативных методов исследования молекулярных движений является релаксационная спектроскопия ЯМР. Однако, не смотря на то, что в расплавах линейных полимеров проведено большое количество экспериментальных исследований по магнитной релаксации [1-8] и создан ряд теорий, описывающих движение молекул [4, 9-12] и ЯМР-релаксацию [1-4, 13-15] в таких системах, однозначной интерпретации полученных данных не существует и по сей день.

Наглядным способом описания результатов эксперимента по ядерной магнитной релаксации в полимерах является представление их в виде спектра времен корреляции (СВК) [15, 16]. Цель данной работы заключается в том, чтобы для линейных полимеров построить СВК в максимально широком диапазоне времен корреляции и по форме и параметрам этого спектра оценить действенность теории Доя-Эдвардса (Д-Э). Для этого нами проведено комплексное исследование ЯМР-релаксации в полиизопреновом каучуке.

Результаты и обсуждение

В качестве объектов исследования служили образцы узких фракций цис-1,4-полиизопренового каучука со средневесовой молекулярной массой М\ = 576 000 (образец 1), ЛД = 735 000 (образец 2) и ЛД = 999 000 (образец 3) с показателями полидисперсности 1,09, 1,04 и 1,05, соответственно. В эксперименте, используя импульсную последовательность Хана 9О°о-т-18О°9о, был снят спад поперечной намагниченности (СПН), методом восстановления намагниченности после действия последовательности импульсов 90°-т-90° измерено время спин-решеточной релаксации (Д). Кроме того, проведены измерения времени релаксации поперечной намагниченности Де/в отклике на модифицированную [17] импульсную последовательность MW-4 (9О°_о-(т/2-180°₉₀—т/2—90° 9о-т/2-18О°9о-т/2-)„) в широком диапазоне раздвижек между импульсами т. Измерения проведены на импульсном спектрометре, работающем на резонансной частоте протонов 25 МГц при температурах 22+160°С. Для определения времен релаксации Т_х и Д_еу производилась запись соответствующих релаксационных кривых в режиме трехкратного накопления. Начальная часть спада поперечной намагниченности регистрировалась в режиме десяти-, средняя - двадцати-, а конечная - пятидесятикратного накопления. При этом каждая часть СПН измерялась в своем режиме усиления. Ошибка в определении времен Д и Д_еГ не превышала 4,5 %, а в определении Д-1,5 %. При каждой температуре время Д, измеренное в образцах 1-3, совпадало в пределах ошибки эксперимента.

На рис. 1 и 2 в полулогарифмическом и линейном масштабах, соответственно, представлены спады поперечной намагниченности, полученные в образце 3 при различных температурах. В образцах 1 и 2 наблюдаются аналогичные СПН. Как видно из этих рисунков, спад поперечной

10 ³~i                  ।        ।        ;        ।        ।        ।         ।                            । I :        ¹ i : i i i i

t, MC

Рис. 1. Спад поперечной намагниченности в полулогарифмическом масштабе в образце 3 при температурах: 22 (1), 40 (2), 60 (3), 80 (4), 100 (5), 120 (6), 140 (7) и 160 (8) °C. Линии - рассчитанные СПН

намагниченности состоит из медленно - (АДО) ^и быстрозатухающей (Л₂ь(0) компонент, что свидетельствует о том, что спиновая система состоит из двух подсистем, обладающих своими релаксационными характеристиками. В последующих расчетах медленнозатухающая компонента АДО была аппроксимирована экспонентой и СПН был принят в виде

А (0 = Аб (0+Аа (О

= Ai(0 + pexp(--J-), (1)

где р - доля медленнозатухающей компоненты в общем спаде, Т_2а - время поперечной релаксации для медленнозатухающей компоненты. Далее путем вычета из общего СПН медленнозатухающей компоненты была получена компонента A^tY Ее время затухания в е раз было обозначено как Т₂. На рис. 3 для образца 3 при температуре 80 °C приведен общий спад А₂(0 и его компоненты A_2a(t) и А₂ь(1).

Поскольку, как это видно из рис. 1-3, быстротухающая компонента является преобладающей, в последующих расчетах мы положили, что время Т2 относится ко всей спиновой системе образца.

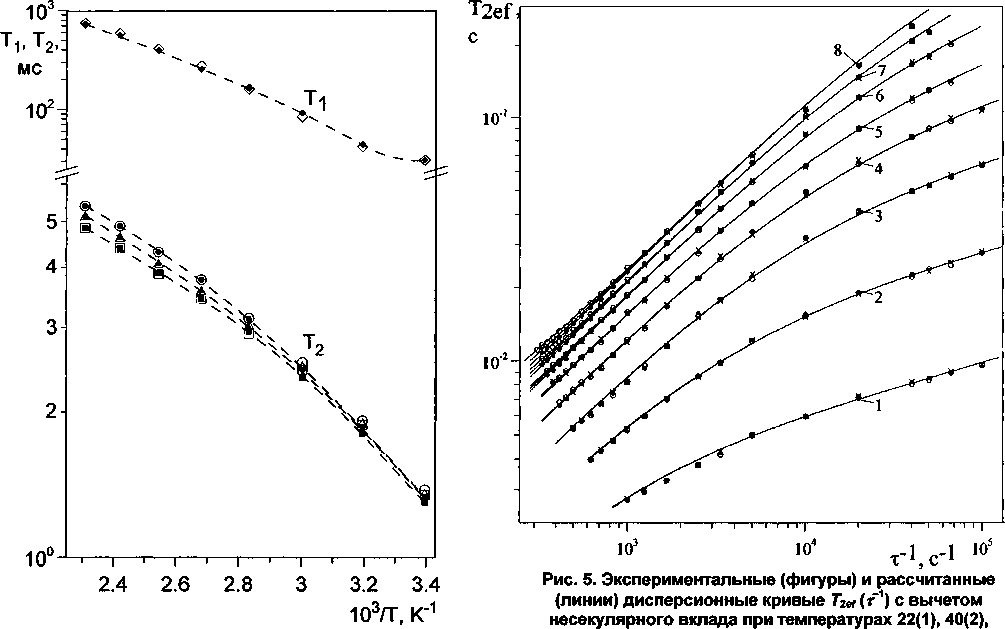
На рис. 4 представлены зависимости времени спада поперечной намагниченности Т2 в образ цах 1, 2 и 3 и времени Т\ от температуры. Пунктирные линии нанесены для удобства визуального

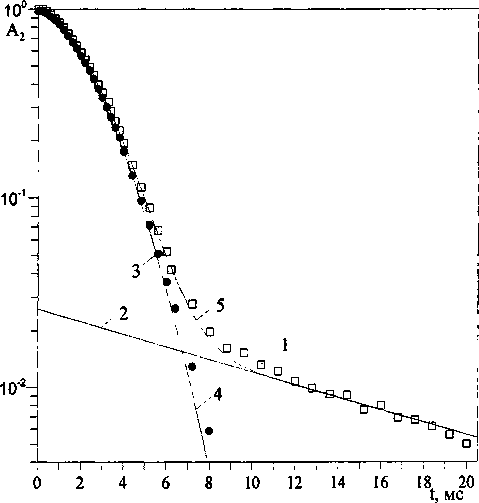
Рис. 3. Результат разложения на компоненты СПН в образце 3 при 80 °C: 1 - экспериментальный СПН A2(f), 2 - медленнозатухающая компонента A2a(Q = pexp(-t/T2a), 3 - экспериментальная короткая компонента Д2ь(1), 4 - рассчитанная по (4) короткая компонента Д2ь(0, 5 - сумма рассчитанной Д2ь(0 и функции Д2а(0

наблюдения.

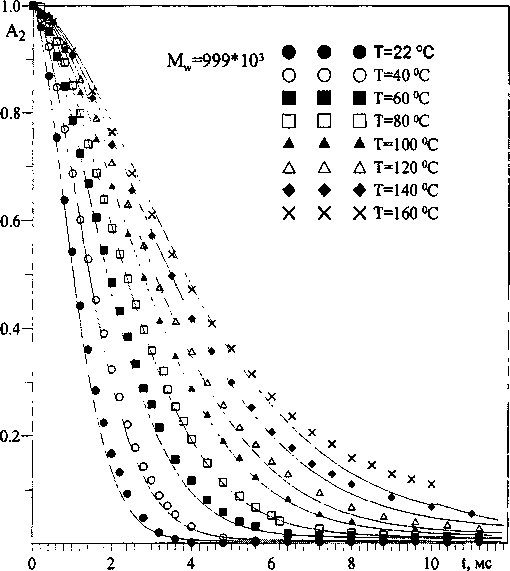
Рис. 2. Спад поперечной намагниченности в линейном масштабе в образце 3 при температурах: 22, 40, 60, 80, 100,120,140 и 160 °C. Линии - рассчитанные СПН

Для описания полученных результатов мы исходили из предположения, что спиновая система однородна, распределение локальных магнитных полей гауссово и движения ядерных спинов, связанных диполь-дипольным взаимодействием, представляются спектром времен корреляции G(r_c) или F(S), где

8 = 1п(гс/тс0).                                    (2)

Модифицированные с учетом СВК выражения для Т^ и спада поперечной намагниченности A^f) были записаны в виде [19, 20]

Tief                                                                       (3)

о л26(?)=ехр

-1 + ехр

где о² - второй момент жесткой решетки. Для Т_х было использовано соотношение, учитывающее СВК в форме функции Фуосса-Кирквуда (Ф-К) [16]:

Тх

2_2^|   (®₀Т _{с 0}/

3 ®о |_1 + (щ0тс0)

k^cof

l-b^r^

где ш₀- циклическая резонансная частота, Р - параметр формы спектра Ф-К (0 <  Р < 1).

В минимуме Timm экспериментальное значение (31 мс) превышает расчетное. Это обусловлено тем, что в высокочастотной части реального СВК на большом удалении от наивероятнейшего времени корреляции т_со имеются компоненты с более высокими интенсивностями, чем в спектре Ф-К с данными параметрами. Поэтому при последующих вычислениях перед функцией G(t_c) был введен поправочный множитель к= КОЗ-сйо^Дпип^о²) [18] ср = 0,8.

На рис. 5 приведены дисперсионные зависимости Т^^^-) после вычета из них несекулярного вклада, рассчитанного из измеренного в эксперименте времени спин-решеточной релаксации в лабораторной системе координат согласно процедуре, описанной в [18]. Полученные дисперсионные зависимости были сведены в объединенную дисперсионную кривую (ОДК), приведенную на рис. 6.

При низких температурах совпадение кривых было частичным, а при высоких - полным. В связи с этим ОДК была разделена на высокотемпературные (100-160 °C) для каждого образца и ряд низкотемпературных для каждой температуры (22, 40, 60 и 80 °C) и каждого образца. При высоких температурах между дисперсионными кривыми существовали различия, обусловленные разницей в молекулярных массах. Для последующей обработки из высокотемпературной ОДК были удалены все провисающие низкочастотные участки. Во время построения ОДК были определены коэффициенты относительного сдвига дисперсионных кривых по осям частот к, равные отношениям наивероятнейших времен корреляции т^.

После этого подбирался СВК с помощью подгонки функции T^/t"¹) (3) - теоретической дисперсионной кривой (ТДК) под ОДК и теоретических значений 7г и Т_х под измеренные в эксперименте. Подгонка проводилась отысканием минимума средне-квадратичного относительного отклонения (СКО). Теоретические Т₂ определялись по уменьшению в е раз спадов АцАГ), рассчитанных согласно (4). В высокочастотной части СВК представлял собой спектр Ф-К, затухающий на крыле по закону F(S) ~ exp(-/?S). При определенных значениях 8, закон затухания крыла изменялся на exp(-a,S). Спектр претерпевал изломы в точках Si, 8_г и S3. При некотором значении 8/ спектр обрывался.

Подгонка осуществлялась в несколько этапов. 1. а) Подгонка ТДК под ОДК при ^=0,8 для температуры 160 °C и получение СВК и t_cq. При этом параметры СВК «1 = 0,5, «2 = 0,25 и «з = 0,43 были заданными, a S_x, Si, S3 и Sf- подгоночными, б) Расчет т_со по коэффициентам к для всех температур проведения эксперимента. 2. Уточнение Р и т_со для всех температур по минимуму СКО для Т_х и T^ef и новая подгонка ТДК под ОДК для температуры 160 °C с параметрами подгонки S_x, Si, S3, Sf и «ь 3. Коррекция ОДК - уточнение к по отысканию минимума отклонения ТДК от ОДК. 4. Повторение этапов 2 и 3 до тех пор, пока СКО не достигнет минимума. 5. Коррекция и последующая фиксация на одном уровне параметров наклона а_х, аг и а₃ для высоких температур и для всех образцов.

60(3), 80(4), 100(5), 120(6), 140(7) и 160(8) °C. Открытые кружочки - образец 1. Крестики - образец 2. Заполненные кружочки - образец 3

Рис. 4. Температурные зависимости времен релаксации Г| и Тг. Т<. экспериментальные данные (открытые ромбики) и рассчитанные значения (заполненные ромбики). Т₂: экспериментальные данные для образца 1 (M_w = 576-103) (открытые квадратики), образца 2 (M_w = 735-103) (открытые треугольники) и образца 3 (М„= 999-103) (открытые кружочки); рассчитанные значения для образца 1 (заполненные квадратики), образца 2 (заполненные треугольники) и для образца 3 (заполненные кружочки)

6. Построение окончательных вариантов спектра и ТДК для высоких и низких температур для всех образцов. Этапы 1-4 проводились на высокотемпературной ОДК образца 3.

В результате подгонки было получено близкое к стартовому (0,8) значение Р = 0,7905±0,0002. Параметры «1 и а₂ для всех образцов найдены равными 0,48 и 0,25, соответственно. Наклон «з был задан равным 0,43. СКО не превышало 4 %. Чтобы оценить ошибки - стандартные отклонения подгоночных параметров, для каждого образца в отдельности была проведена процедура подгонки на искусственно сгенерированных значениях Т₂, Т_х и ОДК с гауссовым разбросом точек и дисперсией, равной дисперсии, полученной при подгон-

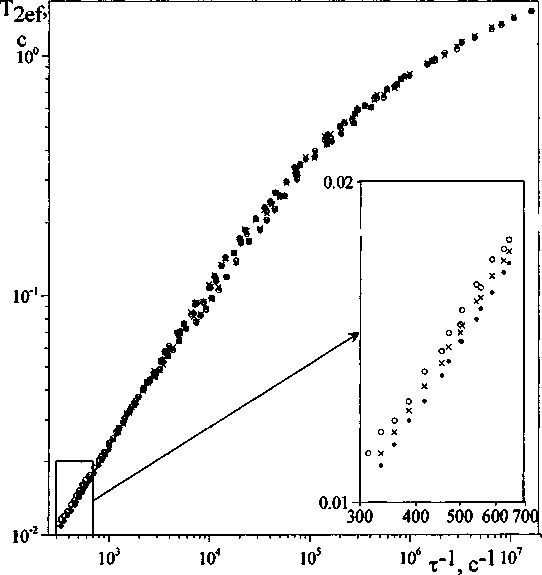
Рис. 6. Объединенная дисперсионная кривая, приведенная к температуре 160 °C. Заполненные кружочки - образец 1.

Крестики - образец 2. Открытые кружочки - образец 3

ке данных под реальный эксперимент. Ошибки косвенных измерений вычислялись по общепринятым правилам.

ю0-^

F(S)|

Зх10"Ч

10'

10"2

10'3

Ю^^бхЮ"6;

35x10'

2x10"5

. 0.79

Ю'5Л и

। 1

। 1 \

। 1 2 г

' 3

а=0.25

■          1 :                4 ' .

:           1                                           1 5 '

S21 S22 S23 S24 S25

тт—; I : I I । : > I I । I I I I । I ।

12 л 13

14 i

-2 0

\ а=0.48

а=0.25

Ю’^ЗхЮ^

I s

10"5 54xio4v

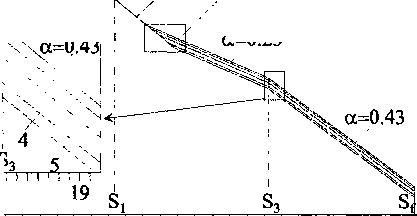
Рис. 7. Спектры времен корреляции, полученные подгонкой теоретических Т2> Л и дисперсионных зависимостей ТгеХт"1) под экспериментальные в образце 3 для темпера-тур: 22(1), 40(2), 60(3), 80(4),100-160(5) °C

2 4 6 8 10 12 14 16 18 20 22 24 26 s

На рис. 7 приведен найденный СВК, а в табл. 1 - средние по температурам параметры Si, S₂, S3 и S/. При обработке низкотемпературных ОДК в качестве Si, S3 и S/ были взяты средние значения величин St, S3 и S/, полученных при высоких температурах, а подгоняемым параметром служило только S₂. Усредненное по образцам значение S₂ представлено в табл. 2. На рис. 5 приведены полученные в результате подгонки теоретические дисперсионные кривые. На рис. 3 приведена рассчитанная по (4) функция А₂ь(Д На рис. 1, 2 и 3 нанесены СПН, сложенные из рассчитанных по (4) функций ^2»(0 и медленнозатухающих компонент Л_2о(0- Как видно из этих рисунков, не смотря на то, что в процедуре подгонки участвовали только значения Т₂, а не сами СПН, теоретические кривые оказались достаточно близкими к экспериментальным.

Полученные в результате под

гонки достаточно низкие значения среднеквадратичных отклонений, небольшие различия между рассчитанными и экспериментальными значениями Т_х, Т₂, T_2ej и спадами поперечной намагниченности свидетельствуют о достаточно высокой степени согласованности разных экспериментальных данных между собой и об удовлетворительном согласии теории с экспериментом.

Таблица 1 __________ Параметры СВК при высоких температурах и рассчитанные из них величины q, Z, М_е, N_e,svib ______

Образец	1	2	3
Л/-103	576	735	999
51	9,37±0,02	9,37±0,02	9,37±0,02
Si	12,78±0,03	12,78±0,02	12,78±0,03
S3	17,1±0,1	17,6±0,1	18,3±0,3
sf	24,3±0,8	26±1	27±2
<7-10"4	1,53±0,02	1,54±0,02	1,55±0,02
Z	49±3	60±4	80±20
Л/е-10'2	118±6	122±7	120±20
Ne	48,7±0,4	48,3±0,4	48,2±0,4
S	3,6±0,2	3,7±0,2	3,6±0,6
	3,6±0,3	3,7±0,3	3,6±0,5

Сравним полученные результаты с предсказаниями теории Доя-Эдвардса (Д-Э) [21]. Отнесем точки излома в СВК Si, S3, и S/ соответственно к характерным временам этой теории: т_е -времени начала действия зацеплений, т_д - максимальному времени в спектре раузовских мод и т^ - времени освобождения от зацеплений, считая их, связанными друг с другом соотношением (2).

В табл. 1 приведено число зацеплений Z в молекуле, рассчитанное по базовой формуле теории Д-Э tr = Z2re, и молекулярная масса полимерной цепи между зацеплениями Ме = Mt ! Z,. Найденное нами среднее значение (Л7е) = (12±2)-103 близко к Ме, полученному равным 9,5-103 и 10-103 в [4] в двух разных экспериментах. Отношения молекулярных масс Мз.М2;М\=\,13\ 1,28:1 и числа зацеплений Z3\Z2.Z\ = (1,8±0,4):(1,2±0,3):1 в пределах ошибки эксперимента также совпадают. В табл. 1 и 2 приведена величина q - относительная доля спектра, заключенного между точками спектра Si и Sj, равная доле остаточного д-д взаимодействия, усредняемого движениями с временами корреляции выше те, и число сегментов Куна Ne, заключенных между двумя последовательными зацеплениями, рассчитанное по формуле [22]

N_e=3K5q^Xi^ .                                (6)

Пользуясь полученными Ne и Z, мы рассчитали число мономерных звеньев в сегменте Куна согласно s = M,/(mNeZt),                               (7)

где т - масса мономерного звена. Найденные s помещены в табл. 1 и 2. Полученные s попали в середину диапазона ожидаемых значений: 2 < s < 5. Эти факты свидетельствуют об удовлетворительном согласии теории Д-Э с экспериментом.

Из табл. 2 видно, что при низких температурах s падает с повышением температуры, что, очевидно, связано с возрастанием гибкости полимерной цепи, обусловленной увеличением амплитуды крутильных колебаний [23].

В табл. 1 приведен показатель степени А, входящий в другое базовое соотношение теории Д-Э:

rrf=3Z\.                              (8)

Средние по образцам значения параметров Sz, q, Ne и s при низких темпе				Таблица 2 ратурах
7, °C	22	40	60	80
Si	11,2±0,1	11,55±0,05	11,90±0,03	12,45±0,03
<М04	1,80±0,03	1,716±0,009	1,654±0,005	1,577±0,003
Ne	44,8±0,3	45,8±0,2	46,6±0,1	47,8±0,1
3	3,92±0,02	3,83±0,01	3,76±0,01	3,67±0,01

Как и ожидалось [24], полученное (А) = 3,6±0,4 превышает предсказываемое теорией Д-Э значение 3. Отличием от теории Д-Э является также и то, что наклон участка спектра перед первым изломом р равен не единице [25], а 0,79, и что участку спектра с наклоном а = 0,25, соответствующего рептации, предшествует участок с более крутым наклоном а = 0,48. Первое мы связываем с неидеальностью полимерной цепи - пренебрежением объемными взаимодействиями между звеньями и сегментами в теории Рауза, а второе - с плавным переходом от раузовской диффузии к рептации.

Выводы

• 1.    В линейных полимерах - узких фракциях цис-1,4-полиизопренового каучука различных молекулярных масс (Л/i = 576 000, М_г = 735 000 и М^ = 999 000) в диапазоне температур 22160 °C сняты спады поперечной намагниченности, измерено время спин-решеточной релаксации Ту и получены дисперсионные зависимости времени Т^ в широкой области раздвижек между импульсами. Спад поперечной намагниченности разложен на две компоненты и определено время затухания короткой компоненты Ту.

• 2.    Дисперсионные зависимости Т^/т"¹) сведены в объединенную дисперсионную кривую (ОДК). При низких температурах (22-80 °C) низкочастотные участки дисперсионных зависимостей выпадают из ОДК, что свидетельствует о частичном нарушении принципа температурно-частотной эквивалентности. В связи с этим ОДК разбита на высокотемпературную и ряд низкотемпературных.

• 3.    Произведена подгонка теоретических Ту, Ту и Тге/Л¹) под экспериментальные Ту и Т₂ и объединенные дисперсионные кривые, в результате чего построены высокотемпературный и ряд низкотемпературных спектров времен корреляции (СВК).

• 4.    Анализ найденных СВК показал, что динамика полимерных молекул в первом приближении описывается трубно-рептационной моделью Доя-Эдвардса. Из параметров спектра рассчитаны число зацеплений в молекуле Z, молекулярная масса участка цепи между зацеплениями М_е, количество сегментов Куна между зацеплениями N_e и число мономерных звеньев в сегменте Куна з. Найдено, что в пределах ошибки измерений совпадают отношения молекулярных масс Му;.Му.Му=\,ПЗ'. 1,28:1 с отношениями чисел зацеплений

• 5.    Показано, что причиной частичного нарушения принципа температурно-частотной эквивалентности при низких температурах (22-80 °C) является изменение длины сегмента Куна.

Z₃:Z₂:Zi=(1,8±0,4):(1,2±0,3):1 и полученные значения М_е с литературными. В то же время, в противоположность с предсказаниями теории Доя-Эдвардса участок в спектре, соответствующий раузовской диффузии между зацеплениями, имеет меньший наклон, а показатель А в соотношении та = 3Z\_e больше 3.