Исследование механизмов формирования поперечных структур оптического поля в широкоапертурных лазерах

ляция микро- и наночастицами, управление характеристиками лазерного излучения. Вследствие подобных различий в требованиях к свойствам лазерного пучка, встает проблема классификации возможных режимов генерации широкоапертурных лазеров и управления процессами возникновения структур оптического поля. В данной работе ставилась задача изучения механизмов, ответственных за распад пространственно-однородных режимов генерации и спонтанное формирование поперечных оптических структур, а также определения характерных размеров получаемых структур.

В качестве математической модели широкоапертурного лазера использовалась полукласси-ческая система уравнений Максвелла-Блоха, которая описывает динамику оптического поля во времени в поперечном сечении выходного пучка с учетом отстройки частоты генерации от центра линии усиления для лазера бегущей волны, работающего на одной продольной моде плоскопараллельного резонатора и имеющего однородно уширенную линию:

' a e— = ia A± E + a( P - E), a t

P = -( 1 + iS)P + DE ,

— = -уГD - r + 1 (E*P + EPa t      '           2V

где E, P, D - безразмерные огибающие электрического поля, поляризации и инверсии населённости соответственно; у = уII / у± и a = k I у 1 , где У1, УII и k — скорости релаксации поляризуемости, инверсии населённости и электрического поля соответственно; 5 = (^21 - ^)। У1 — расстройка между центром линии усиления и частотой лазерной генерации, обезразмеренная на ширину линии усиления; А 1 - двумерный оператор Лапласа, учитывающий расходимость пучка из-за дифракции; a = c2 1(2^у 1 d 2) — дифракционный параметр, где d - ширина апертуры; r – накачка, нормированная на пороговое значение [5].

Как было ранее показано [6], когда величина накачки превышает значение, соответствующее порогу генерации, в системе (1) при отрицательном знаке отстройки частоты устанавливается пространственно-однородное решение:

ся к анализу устойчивости образующегося предельного цикла соответствующей точечной системы относительно пространственно-неоднородных возмущений.

Рассмотрим структуру данного предельного цикла. Для этого удобно перейти от исходных переменных в системе (1) к квадратичным переменным:

I = E • E*= E\2; U = P • P*= P\2; D;

V = 2 (EP * + PE *); W = 2 i (E * P - P * E), после чего получим следующую систему:

' di = ,a(V -1),

D

= 1 +

(—гV a + 1)

E = (r - D )0'5 • e’iQt;

dU = 2(DV - U), dt

dV

---= DI + aU - (a +1) V - 5W. (3) dt

к = (a - iQ) • E

P                  ;

a

Q =

5a

a +1

---= 5V - (a +1) W, dt

dD

---= - у ( D - r + V ) .

dt

В результате анализа устойчивости решения (2) было показано, что для него характерны два типа неустойчивостей – волновая и неустойчивость Хопфа. Случай волновой неустойчивости ранее уже подробно рассматривался [7, 8]. Однако наибольший интерес здесь представляет случай неустойчивости Хопфа, так как при этом появляется возможность установления однородной генерации. Тогда исследование динамики сводит-

Данная система имеет устойчивый предельный цикл, которому в модели (1) отвечает генерация пространственно-однородного излучения. На рис. 1 представлена бифуркационная диаграмма для системы (3) при фиксированных значениях параметров a = 2, у = 0.1, r = 30 и различных значениях параметра 5 .

Однако, как было показано, данный предельный цикл в системе (1) имеет непериодическую структуру и представляет собой либо хаотичес-

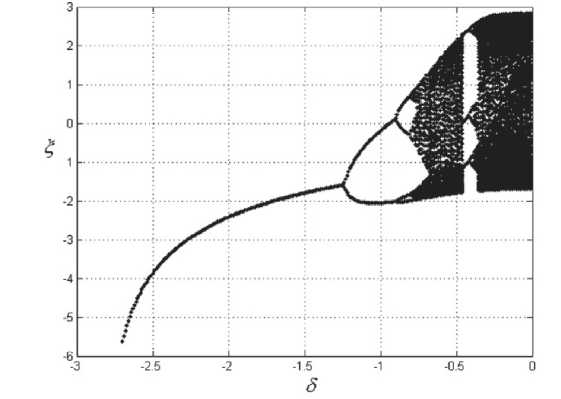
Рис. 1. Бифуркационная диаграмма при a = 2, у = 0.1, r = з0

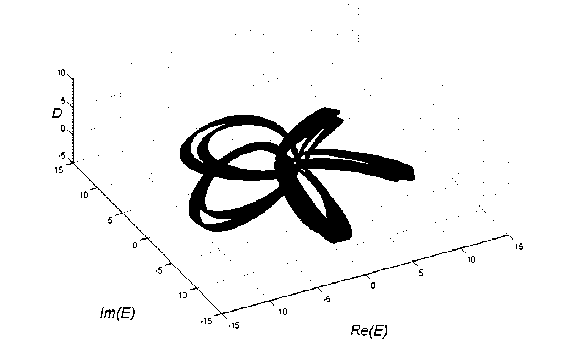
Рис. 2. Аттрактор модели (1)

при a = 2, у = 0.1, 5 = - 1, r = 30

кий аттрактор, либо устойчивый двумерный тор (см. пример на рис. 2), вследствие чего стандартная процедура анализа его устойчивости методом Флоке [9] оказывается неприменимой.

В связи с этим было предложено обобщение данного метода, которое основано на исследовании эволюции малого возмущения, соответствующего определенной моде, с проведением процедуры ортогонализации по достаточно длинной реализации аттрактора. С помощью данного подхода для аттрактора были построены диаграммы зависимости показателей Флоке от волнового числа возмущения. При этом отсутствие положительных показателей должно было указывать на установление в модели режима однородной генерации, а наличие положительных максимумов – на образование неоднородных оптических структур, характерные размеры которых должны соответствовать волновому числу моды, дающей максимум на диаграмме.

• 3.    ОБРАЗОВАНИЕ ПОПЕРЕЧНЫХ СТРУКТУР

На рис. 3 приведена диаграмма показателей Флоке для значений параметров a = 2, у = 0.1, д = - 2, r = 30 , при которых показатели отрицательны при всех значениях волнового числа возмущения. Непосредственное численное моделирование системы (1) показало, что в этом случае в системе действительно устанавливается режим генерации пространственно-однородного излучения. При этом характер временной зависимости интенсивности излучения на выходе лазера определяется по структуре аттрактора точечной системы (3). В данном случае наблюдался периодический режим генерации, что согласуется с бифуркационной диаграммой, представленной на рис. 1. Ниже на рис. 4-5 приведены временная зависимость интенсивности излучения и поперечный профиль интенсивности в

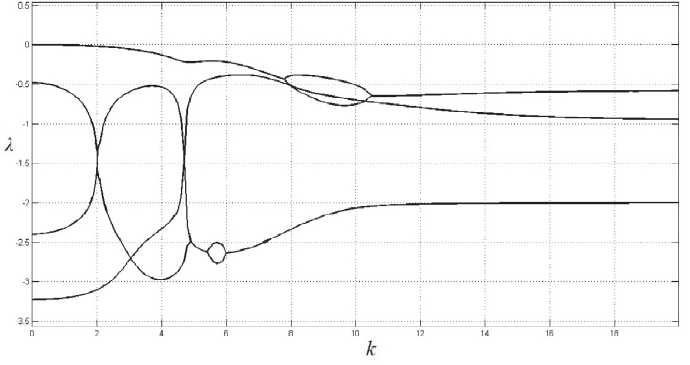
Рис. 3. Диаграмма зависимости показателей

Флоке X от волнового числа возмущения k при значениях параметров a = 2, у = 0.1, д =- 2, r = 30

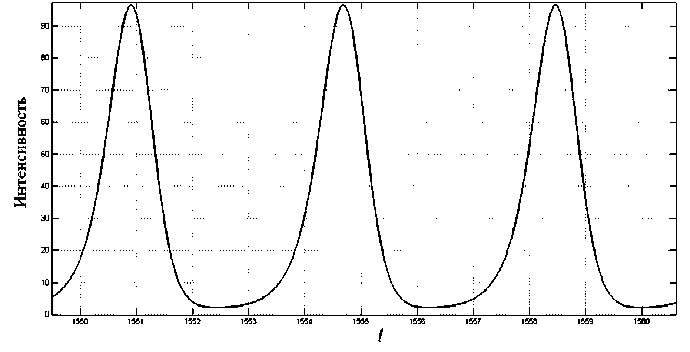
Рис. 4. Временная зависимость интенсивности излучения на выходе лазера

при a = 2, у = 0.1, д = -2, r = 30

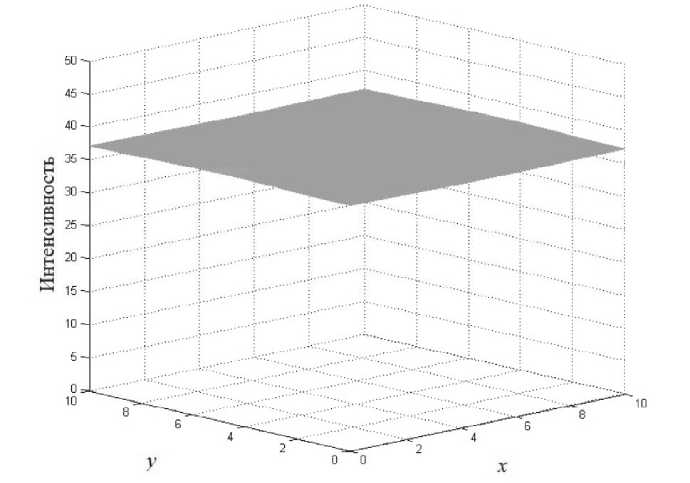
Рис. 5. Распределение интенсивности при a = 2, у = 0.1, д = -2, r = 30

установившемся режиме генерации.

В случае же наличия положительных показателей Флоке реализуется один из двух возможных режимов генерации, сопровождающихся появлением неоднородных оптических структур: формирование спиральных волн или структур типа модулированной стоячей волны. Так, на рис. 6-8 показаны максимум диаграммы показателей Флоке, поперечное распределение интенсивности и картина дальнего поля для значений параметров a = 2, у = 0.1, д = - 0.4, r = 30 , при которых наблюдается распад режима однородной генерации с образованием спиральных волн.

Было также установлено, что характерные пространственные размеры получаемых структур удовлетворительно согласуются с размерами, соответствующими критической моде, что иллюстрируют рис. 6 и 8.

• 4.    ЗАКЛЮЧЕНИЕ

В работе показано, что формирование поперечных структур в модели широкоапертурного лазера, описываемой системой уравнений Максвелла-Блоха, возможно при неустойчивости как

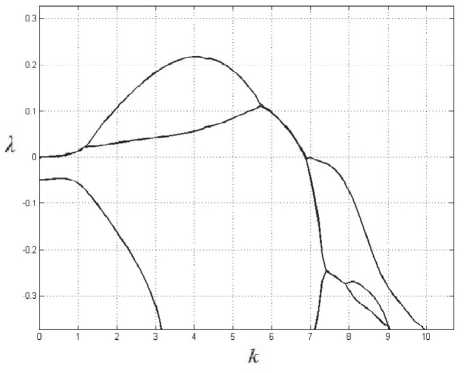
Рис. 6. Положительные показатели Флоке

при а = 2, у = 0.1, 5 = -0.4, r = 30

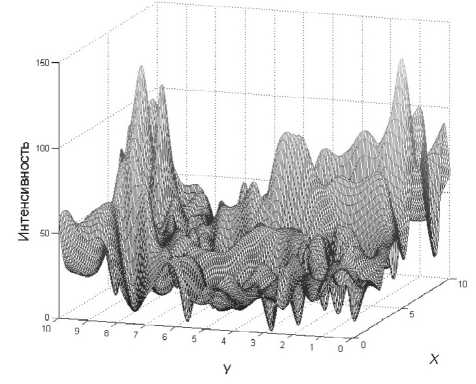
Рис. 7. Распределение интенсивности

при а = 2, у = 0.1, 5 = -0.4, r = 30

однородного стационарного режима, так и циклического режима однородной генерации по отношению к малым возмущениям. Для выполнения анализа устойчивости в последнем случае было предложено и реализовано обобщение стандартного метода Флоке. С его помощью были построены диаграммы показателей Флоке, позволившие выделить области параметров с разной динамикой излучения лазера.

Рассмотрен вопрос о том, какие структуры могут наблюдаться для каждого типа неустойчивости однородных режимов генерации. Получено соответствие между предсказанными пространственными размерами структур и полученными при численном моделировании, что позволяет рассчитывать на возможность применения проведенного анализа для практических задач управления характеристиками лазерного излучения.

Работа частично поддержана Минобрнауки РФ, государственное задание на выполнение ра-

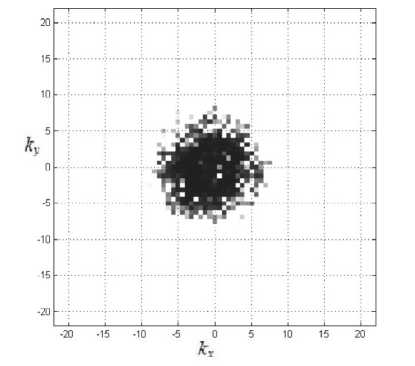
Рис. 8. Спектр оптического поля при а = 2, у = 0.1,5 = -0.4, r = 30

бот на 2012-2014 годы, шифр 2.560.2011 и ФЦП “Научные и научно-педагогические кадры инновационной России” на 2009-2013 гг., ГК № 14.740.11.0999, 14.740.11.1140, соглашения 14.B37.21.0767, №14.132.21.1423, 14.132.21.1440 и грантами РФФИ 13-01-97001 р_повол-жье_а, 1301-97005 р_поволжье_а, 12-01-31229 мол__а и НИР № ГР 01201156352.

• 1 .    Кренц А.А., Молевич Н.Е. Каскад бифуркации удвоения тора в лазере с отстройкой частоты // Квантовая электроника. 2009. Т. 39, № 8. С. 751-756.

• 2 .    Кренц А.А., Анчиков Д.А. Решетки вихрей в широкоапертурных лазерах // Известия Самарского научного центра РАН. 2012. Т. 14, № 4. С. 201-205.

• 3 .    Chen Y.F., Lan Y.P. Spontaneous pattern formation in a microchip laser excited by a doughnut pump profile // Appl. Phys. B. 2002. Vol. 75. P. 453-456.

• 4 .    Cabrera E., Calderon O.G., Melle S., Guerra J.M. Development of spatial turbulence from boundary-controlled patterns in class-B lasers // Phys. Rev. A. 2006. Vol. 73. 053820.

• 5 .    Ханин Я.И. Основы динамики лазеров // М.: Наука. Физматлит, 1999. 368 с.

• 6 .    Jacobsen P.K., Moloney J.V., Newell A.C., Indik R. Spacetime dynamics of wide-gain-section lasers // Phys. Rev. A. 1992. Vol. 45. № 11. P. 8129-8137.

• 7 .    Заикин А.П., Кургузкин А.А., Молевич Н.Е. Периодические автоволновые структуры в широкоапертурном лазере с отстройкой частоты. 1. Бифуркационный анализ // Квантовая электроника. 1999. Т. 27. № 3. С. 246-248.

• 8 .    Заикин А.П., Молевич Н.Е. Влияние скорости кроссрелаксации на поперечную динамику излучения широкоапертурного лазера // Квантовая электроника.

2004. Т. 34. № 8. С. 731-735.                                near a Hopf-Wave interaction in a chemical model //

• 9 .    Pena B., Bestehorn M. Two-dimensional wave patterns Eur. Phys. J. Spec. Topics. 2007. Vol. 146. P. 301-311.

• ¹    Samara State Aerospace University named after Academician S.P. Korolyov (National Research University)

• ²    Samara Branch of Physical Institute named after P.N. Lebedev, RAS

Anton Krents, Candidate of Physical and Mathematical

Sciences, Assistant Lecturer at the Physics Department,