Исследование метода восстановления параметров линейных однородных веществ по экспериментально измеренной частотной зависимости поверхностного импеданса
Автор: Глухов А.Ю., Негинский И.В.
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Радиофизика
Статья в выпуске: 13, 2010 года.
Бесплатный доступ
Рассмотрен абсолютный метод определения параметров линейных однородных веществ по измерениям частотной зависимости поверхностного импеданса цилиндрических образцов. Оце- нено влияние точности определения импеданса и радиуса образца на полученные при решении обратной задачи значения проводимости, магнитной и диэлектрической проницаемостей.
Решение обратной задачи, проводимость, магнитная проницаемость, диэлектрическая проницаемость, поверхностный импеданс
Короткий адрес: https://sciup.org/14968642
IDR: 14968642 | УДК: 621.317.33+621.317.335.3+621.317.411
Текст научной статьи Исследование метода восстановления параметров линейных однородных веществ по экспериментально измеренной частотной зависимости поверхностного импеданса
В настоящее время современные методы и реализованные на их основе приборы позволяют получить только один из параметров материала [2-5] - либо относительную проводимость о , либо относительную магнитную проницаемость ц , либо относительную диэлектрическую проницаемость е , в то время как важным является знание всех трех параметров. Таким образом, становится актуальной задача разработки и технической реализации экспериментального взаи-моиндукционного метода, позволяющего одновременно получить все три параметра материала. Метод позволяет, исходя из экспериментально полученной зависимости поверхностного импеданса цилиндрического образца, вычислить параметры среды. Он может быть применен для определения параметров линейных однородных материалов (как проводников, так и диэлектриков), что делает его особенно ценным как в научном, так и практическом плане.
Поверхностный импеданс является наружной характеристикой среды, позволяющей судить об амплитуде и фазе отраженной волны, не интересуясь внутренними микроскопическими процессами.
Решение электродинамической задачи расчета поверхностного импеданса Z ( ю ) в случае линейной однородной среды требует знания лишь параметров материала образца. Из уравнений Максвелла и материальных уравнений среды можно получить [1], что частотная зависимость поверхностного импеданса цилиндрического образца радиуса R проводимостью о , относительной диэлектрической проницаемостью е и относительной магнитной проницаемостью ц имеет следующий вид:
Z ( ю ) =
—
j ωµµ 0 J 1 ( β R )
-------------------------------------------------- .-------------------------------
(ст + jtoEE 0) J о( eR), где Р2 = -j юцц0(о + j юее0);
ю - частота электромагнитного поля;
R – радиус цилиндрического образца;
J 1, J 0 – функции Бесселя первого рода первого и нулевого порядка соответственно;
ц 0 - магнитная постоянная;
е 0 - электрическая постоянная.
Практический интерес представляет решение обратной задачи – исходя из экспериментально измеренной частотной зависимости поверхностного импеданса определить параметры о , е и ц . Для решения данной задачи вычислим производную Z 'ю :
Z, _ d Z + ( d + j ®ss 0)[( d + j ®ss 0) RZ 2 - j ®uu 0 R - Z ] ® 2 ® ( d + j ®ss 0)
.
Разделяя мнимую и вещественную составляющие импеданса Z = k + jm и его производной Z' _ 1 + jn , получим уравнение:
А о 3 + B о 2 + C ест 2 + D ео + Е е 2 о + F е 2 + G е 3 _ 0
где введены обозначения A, B, C, D, E, F, G :
А _ x 2 R _ ( к 2 - m 2) R,
B _ -2 1® ,
C _ -2 kmR®s 0,
■ D _ 2 ® ( m - n® ) s 0,
E _ 4 x 2 R® 2 8 0 _ 4( к 2 - m 2) R® 2 s 02,
F _ -4( к + 1® ) ® 2 s 02,
G _ -8 kmR® 3 s 3 .
Входящие в (4) коэффициенты могут быть определены экспериментально. Таким образом, имеется принципиальная возможность определить внутренние параметры материала образца о , е и ц исходя из частотной зависимости поверхностного импеданса образца.
Решать уравнение (3) можно различными способами. Воспользуемся избыточностью исходных данных, то есть большим числом экспериментальных значений Z ( го ).
Определим коэффициенты А-G в нескольких точках по частоте: A i = А ( го i )... G i = G ( го i ). Значение производной Z ' ( го ) получим из частотной характеристики Z ( го ), аппроксимировав ее с помощью центральных разностей второго порядка точности.
Тогда соотношение (3) примет вид:
d _- BCDEF^
ACDEF 123456
8 _ - L ( ADEF i2345 d + BDEF 12345 ),
( CD EF 12345
где выражения для коэффициентов ADEF 12345– BDEF 12345 определяются по пяти различным отсчетам Z ( го i ) (см. таблицу).
С математической точки зрения решением является также вариант о = 0. И импеданс, и его производная в этом случае чисто мнимые величины. Решение уравнения (3) тогда примет вид:
|
m, mm. m 2(— + n 1 ) + m 1 (— + n 2) ωω U _-----1H-----, U 0 R ( m 2 - m i ) mm n 1 - n 2 + -1- - (6) ω 1 ω 2 s 0 R ( m 2 - m 2 ) |
Таким образом, получив экспериментальную частотную характеристику поверхностного импеданса цилиндрического образца радиуса R , можно вычислить параметры о , е и ц материала образца.
Оценим методические погрешности данного метода восстановления параметров среды по экспериментальным результатам. При измерениях с помощью экспериментальной установки определяются вещественные и мнимые составляющие комплексного импеданса цилиндрического образца. Также существенным параметром является радиус образца R .
Значения коэффициентов (4) для пяти различных частот ω 1 ... ω 5
|
A 1 = A ( ® 1 ) A 5 = A ( m 5) |
G 1 = G ( ® 1 ) G 5 = G ( « 5 ) |
|
AA 12 = A G 2 - A 2 G 1 , |
AA 56 = A 5 G 6 - A, G 5 , |
|
BB 12 = B 1 G 2 - B 2 G 1 , |
BB 56 = B 5 G , - B 6 G 5 , |
|
CC 12 = C 1 G 2 - C 2 G 1 , |
CC 56 = C 5 G , - C 6 G 5 , |
|
DD 12 = D 1 G 2 - D 2 G 1 |
DD 56 = D 5 G 6 - D 6 G 5 , |
|
EE 12 = E G 2 - E 2 G 1 , |
EE 56 = E 5 G 6 - E 6 G 5 , |
|
FF 12 = F G 2 - F 2 G 1 , |
FF 56 = F 5 G 6 - F 6 G 5 . |
|
AF 23 = AA 12 FF 23 - AA 23 FF 12 , |
AF 456 = AA 45 FF 56 - AA 56 FF 45 , |
|
BF 23 = BB 12 FF 23 - BB 23 FF 2 , |
BF 456 = BB 45 FF 56 - BB 56 FF 45 , |
|
CF123 = CC 12 FF 23 - CC 23 ff12 |
_ CF 456 = CC 45 FF 56 - CC 56 FF 45 , |
|
DF 123 = DD 12 FF - DD 23 FF12 , DF 456 = DD 45 FF 56 - DD 56 FF 45 , |
|
|
EF 23 = EE 12 FF 23 - EE 23 FF 12 , |
EF 456 = EE 45 FF 56 - EE 56 FF 45 . |
|
AEF 1234 = AF 2 3 EF 234 - AF 234 EF 23 , |
AEF 3456 = AF 345 EF 456 - AF 456 EF 345 , |
|
BEF1234 = BF 123 EF 234 - BF 234 EF123 , |
BEF 3456 = BF 345 EF 456 - BF 456 EF 345 , |
|
CEF 1234 = CF 123 EF 234 - CF 234 EF 123 , |
’ " CEF 3456 = CF 345 EF 456 - CF 456 EF 345 , |
|
DEF1234 = DF 123 EF 234 - DF 234 EF123 |
DEF 3456 = DF 345 EF 456 - DF 456 EF 345. |
|
ADEF 2345 = A E F 234 DEF 2345 - AEF 2345 DEF1234 , |
|
|
BDEF 12345 = BEF 234 |
DEF 2345 - BEF 2345 DEF 234 , |
|
CDEF12345 = CEF1234 |
DEF 2345 - CEF 2345 DEF1234 , |
|
ADEF 23456 = AEF 2345 DEF 3456 - AEF 3456 DEF 2345 , b DEF 23456 = b EF 2345 d EF 3456 - BE F3456 DE F2345 , CDEF 23456 = CEF 2345 DEF 3456 - CEF 3456 DEF 2345 . |
|
|
a CDEF 123456 = ad EF 12345 CDEF 23456 - ADEF23456CDEF12345 , BCDEF 123456 = BDEF 12345 CDEF 23456 - BDEF 23456 CDEF 12345 , |
|
Рассмотрим влияние точности определения Z ( м ) и R на вычисленные в рамках метода о , е и ц . Оценим влияние точности определения радиуса на точность восстановления относительной проводимости. Для этого представим о = О о + Ао и R = R о + A R . Подставляя последние выражения в (3) и (4), делая необходимые преобразования, получим следующее выражение для относительной погрешности проводимости:
А с _ x 2с 0 2 A R - 2«ее о km c 0 A R + 2о>ее о( m - n m )
с 0 4 / й х г 0 + 4 ®ее о km c 0 R 0 - 3 x 2 R0 с 2 - 2 m ( m - п® ) ее о '
Производя аналогичные вычисления для ε = ε′ + ∆ε и R = R 0 + ∆ R , можно оценить влияние точности определения радиуса на ошибку восстановления относительной диэлектрической проницаемости ε :
∆ ε x 2 σ 2 ∆ R - 2 ωε ′ ε 0 km σ ∆ R
ε ′ 2 ωε ′ ε 0 km σ R 0 - 2 ωε ′ ε 0 ( m - n ω ) .
Анализ соотношений (7) и (8) показывает, что погрешность для проводимости и диэлектрической проницаемости практически линейно зависит от погрешности определения радиуса образца.
Численное моделирование использования метода восстановления параметров для цилинд- de^aneT а Т адауоа дааеопа R = 4,5 мм дает следующие результаты.
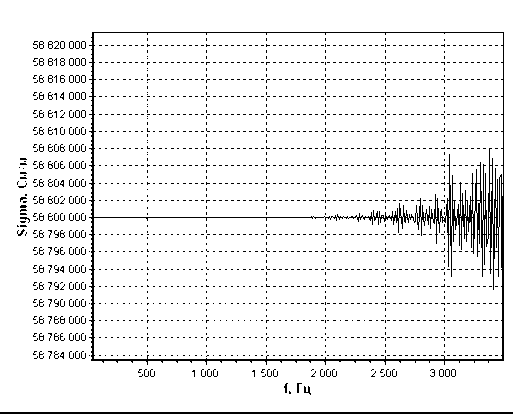
Рис. 1. Зависимость восстановленного значения проводимости Sigma медного образца с проводимостью σ = 58,8 106 См/м
Как видно из рисунка 1, отклонение восстановленного значения проводимости от исходного не превышает 1,4 10–4 %.
Аналогичная ситуация наблюдается и с алюминиевым образцом проводимостью σ = 36 106 См/м (рис. 2). В этом случае ошибка не превышает 4,5 10–5 %.
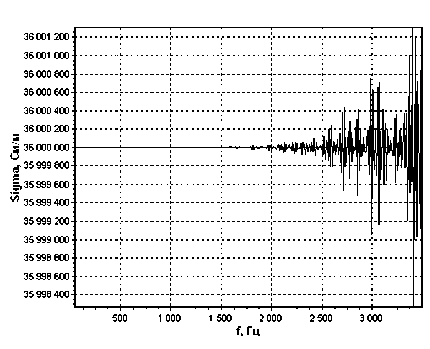
Рис. 2. Зависимость восстановленного значения проводимости Sigma алюминиевого образца с проводимостью σ = 36 106 См/м
Из графиков (рис. 1 или рис. 2) видно, что ошибка в восстановленном значении относительной проводимости цилиндрического образца возрастает с возрастанием частоты. Это связано с особенностью программного расчета самих значений импеданса Z(ω), а не с точностью метода, поскольку для его реализации используются только простейшие арифметические операции.
Таким образом, теоретически обоснована и численно проверена возможность определения параметров материала σ , ε и µ цилиндрических образцов по интегральным измерениям частотной характеристики поверхностного импеданса. Анализ точности метода показывает довольно высокую чувствительность результатов восстановления к погрешности определения радиуса образца.
Список литературы Исследование метода восстановления параметров линейных однородных веществ по экспериментально измеренной частотной зависимости поверхностного импеданса
- Игнатьев, В. К. Измеритель поверхностного импеданса/В. К. Игнатьев, И. В. Негинский//ПТЭ. -1998. -№ 2. -С. 60-66.
- Матвейчук, В. Ф. Измерения электромагнитных свойств материалов с низкими потерями на СВЧ методами диэлектрического резонатора/В. Ф. Матвейчук, С. Н. Сибирцев, Н. М. Карих//Измерительная техника. -2004. -№ 8. -С. 30-35.
- Пчельников, Ю. Н. Радиоволновые методы контроля электромагнитных параметров радиопоглощающих материалов/Ю. Н. Пчельников, А. А. Елизаров//Измерительная техника. -1994. -№ 12. -С. 9-11.
- Сандовский, В. А. Методика измерения и аттестации образцов удельной электрической проводимости/В. А. Сандовский, В. В. Дякин, М. С. Дударев//Измерительная техника. -2005. -№ 9. -С. 59-65
- Чечерников, В. И. Магнитные измерения. Изд. 2-е/В. И. Чечерников. -М.: Изд-во МГУ, 1969. -386 с.


