Исследование методов определения относительных координат группы объектов

Для некоторых применений радионавигации представляет интерес определение относительных координат потребителей, характеризующих расположение взаимное объектов друг относительно друга. Такие задачи могут возникать, например, при определении координат пунктов приема и возбуждения сейсмиче- ских сигналов во время разведки месторождений нефти и газа при использовании трехмерной сейсмической съемки на суше и на морских акваториях [1; 2], а также в системах управления добычей полезных ископаемых, где требуется знание координат мест выработки и вспомогательных объектов, работающих, например, в открытых карьерах или на дражных полигонах [3–8].

Как правило, при выполнении взаимной координатной привязки объектов один из объектов назначается ведущим, относительно которого определяются координаты других объектов, оснащенных бортовыми станциями (БС). Полученные относительные координаты БС при необходимости могут быть пересчитаны в абсолютные, заданные в той или иной системе координат, требуемой при выполнении работ. Для реализации такого пересчета необходимо знание абсолютных координат центра используемой системы координат (СК), а также направления осей данной системы координат. Следует отметить, что при задании направления осей системы относительных координат по направлениям: ось 0 x – на Север, ось 0 y – на Восток, ось 0 z – вниз может быть получена локальная система координат (ЛСК) [9], для которой известны формулы перехода в систему геоцентрических координат (ГЦСК) или в систему географических координат широта-долгота-высота [10].

Исходя из вида измеряемых значений радионавигационных параметров можно выделить несколько методов определения местоположения объектов: дальномерный, квазидальномерный, разностно-дальномерный, пеленгационный, суммарно-дальномерный, а также их комбинации [11].

В данной статье будут рассмотрены три метода определения относительных координат объектов: угломерно-дальномерный, дальномерный и разностнодальномерный. При этом здесь и далее полагается, что задача решается на плоскости, т. е. значение вертикальной координаты для всех станций считается одинаковым. В случае необходимости, для учета разности высот антенн могут быть использованы методы редукции полученных координат на плоскость, используемые при решении задач в морских радионавигационных системах [13].

Для определения координат БС относительно одной опорной станции (ОС) являющейся ведущей опорной станцией, далее в материалах статьи обозначенная как ОС1, находящейся в центре ЛСК, наиболее простым является угломерно-дальномерный метод, поскольку координаты станций определяются относительного одного опорного навигационного пункта, координаты которого могут быть приняты нулевыми, т.е. ведущая опорная станция ОС1 будет находиться в начале координат ЛСК. Для решения задачи определения координат БС данным методом требуется измерение истинных пеленгов (азимутов) az_i с ОС1 к каждой БС, а также дальностей r_i между станциями . При этом значения координат каждой из БС определяются по формулам:

x i = R i ■ cos( az i )

У, = Ri' ^sin( az) ’

где i = 1,…,n – текущий номер БС; n – общее число БС; Ri – измеренная дальность от ОС1 до i-й БС; azi – измеренный азимут направления от ОС1 к i-й БС; xi,yi– неизвестные координаты i-й БС.

Следует отметить, что угломерно-дальномерный метод обладает известным из радиолокации недостатком, состоящим в том, что с увеличением расстояния от ОС1 возрастает погрешность определения координат объекта.

Уменьшение влияния указанного недостатка достигается за счет использования дальномерного метода определения координат объектов. Определение координат в дальномерном режиме работы РНС осуществляется путем решения системы нелинейных уравнений вида:

R i = V ( x oci - x ) 2 + ( У ос( ^- У ) 2 , ⁽²⁾

где Ri – измеренные значения дальности от i-й ОС до БС; xoci, yoci – известные прямоугольные координаты i-й ОС; x,y – координаты БС, подлежащие оп- ределению.

Система уравнений (2) состоит из n уравнений (по числу принимаемых сигналов ОС) с двумя неизвестными, представляющими собой координаты БС на плоскости x0y . Поскольку в системе (2) содер- жится 2 неизвестных, то для ее однозначного решения следует измерить дальности минимум до 2-х ОС.

Следует отметить, что для рассматриваемого дальномерного метода определения координат БС станции в измерениях являются равноправными, т. е. БС измеряет дальности до всех ОС (ОС1, ОС2 и т. д.), число которых, как было указано выше, должно быть больше либо равно двум. При этом начало координат рассматриваемой локальной системы координат ЛСК находится в точке расположения антенны станции ОС1 и в этом смысле данная станция является ведущей как и в рассмотренном выше угломернодальномерном методе.

Другим методом определения координат БС, является разностно-дальномерный, в котором вычисляются разности между значениями задержек или фазовых сдвигов (ФС) сигналов, принятых от ведомых ОС (ОС2, ОС3 и т.д.) и сигналами ведущей опорной станции ОС1 [11, 12]. Система уравнений для определения координат объектов в этом случае имеет вид:

^{A R} i = 'I ⁽ x oci + 1 - x ) 2 ^{+ (} y oci + 1 - y ) 2 ^{+ +} d i + 1,1 - V⁽ xoc 1 - x ) 2 ^{+ (} y oc 1 - ^y ) 2

где i = 1,.., n - 1 - текущий номер измеренного значения разности дальностей; A R i - i значение разности дальностей, d i _{+ 1} 1 - известное расстояние между ведущей ОС (ОС1) и ведомой i +1-й ОС.

С целью моделирования методов и расчета погрешностей определения координат в рассмотренных выше режимах была задана взаимная расстановка станций, относительные координаты которых требовалось затем определить.

При моделировании были заданы следующие исходные данные:

– координаты первой станции, являющейся ведущей опорной (ОС1) для всех исследуемых режимов в ЛСК были заданы равными (0, 0), т. е. данная станция является центром используемой локальной системы координат;

– число БС в системе n = 14;

– максимально возможные расстояния между ОС1 и БС равны 5 км;

– значения азимутов от ОС1 до БС находятся в диапазоне 0–360°.

Полученная в результате расчетов расстановка ОС1 и БС приведена на рисунке. На данном рисунке обозначено положение бортовых станций БС1–БС14, а также опорной станции ОС1 в начале ЛСК.

Моделирование алгоритмов определения места станций в дальномерном и разностно-дальномерном методах осуществлялось по сигналам 3-х или 4-х ОС. При этом приведенная на рис. 1 расстановка ОС и БС сохранялась. В качестве других опорных станций (ОС2, ОС3 и т. д.) использовались станции, выбираемые из БС1–БС14. При этом в качестве ведущей опорной станции ОС1 всегда назначалась станция с координатами (0; 0).

Выбор остальных ОС (ОС2, ОС3 и т. д.) из числа БС осуществлялся двумя способами:

– случайный выбор, в котором в качестве опорных станций использовались первые 2 или 3 БС, в зависимости от требуемого числа ОС (3 или 4 соответственно);

– выбор с оптимизацией, в котором в качестве опорных выбирались БС, обеспечивающие минимальное значение суммарного геометрического фактора оставшихся станций, назначенных бортовыми [11; 12].

На рис. 1 в качестве примера показаны ОС, выбранные случайным образом (отмечены цифрой «3»), и с учетом оптимизации по минимуму геометрического фактора (отмечены цифрой «4»).

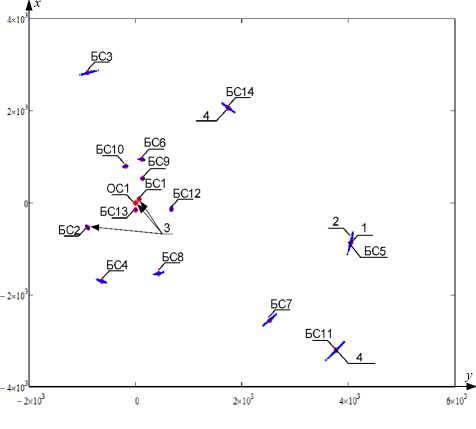
Заданные и измеренные в угломерно-дальномерном режиме значения координат БС

Из полученных результатов видно, что случайный выбор ОС привел к тому, что они оказались расположенными достаточно близко друг к другу и почти на одной прямой. Указанное расположение ОС является неоптимальным с точки зрения ожидаемой погрешности определения координат. В то же время, выбор в качестве ОС станций, обеспечивающих минимизацию суммарного геометрического фактора остальных станций, обеспечивает расстановку ОС на большом расстоянии друг от друга с наилучшим охватом рабочей зоны.

С целью сравнения исследованных методов определения места объектов осуществлялось их статистическое моделирование, при котором рассчитывались значения погрешностей определения координат БС при воздействии случайных погрешностей измерения азимутов и дальностей (угломерно-дальномерный режим), дальностей или разностей дальностей для дальномерного или разностно-дальномерного режимов соответственно. Погрешности измерения азимутов, дальностей и разностей дальностей задавались в виде нормально распределенных случайных величин с нулевым математическим ожиданием и среднеквадратическим отклонением (СКО) погрешности измерения дальности или разности дальностей ст r = 1 м, азимута ст az = 1°. Указанные значения погрешностей вполне достижимы современными дальномерными и радиопеленгационными системами на расстояниях между объектами в несколько километров [14].

На рисунке приведены результаты определения координат БС1–БС14, полученные угломернодальномерным методом. На приведенном рисунке цифрой «1» обозначены истинные значения координат БС, цифрой «2» – координаты, полученные при моделировании по 500 независимым испытаниям.

Из приведенных результатов следует, что, как и ожидалось, для рассмотренного угломерно-дальномерного режима, с увеличением расстояния от ОС разброс значений получаемых координат БС увеличивается, что объясняется возрастанием влияния по- грешности определения направления прихода ст az.

Среднеквадратические отклонения погрешностей определения координат БС определялись по результатам 500 независимых испытаний по следующим фор- мулам:

^ст xi

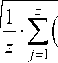
x ij

^^^^^^»

x 0 i ) ² ,

^ст yi

¹ -1l ( y j - y 0 i ) ² z j = 1

где j = 1,.., z - текущий номер испытания; z - общее число проведенных испытаний; x_ij , y_ij – координаты i -й БС, полученные в j -м испытании; x _{0 i} , y _{0 i} – истинные значения координат i -й БС, заданные в соответствии с их расстановкой; ст xi , ст yi - СКО погрешности определения координат ( x , y ) i -й БС.

Значения среднеквадратических погрешностей определения места станций для исследованных методов определения координат объектов

Станция	Угломернодальномерный метод	Дальномерный метод		Разностно-дальномерный метод
		3 ОС	4 ОС	3 ОС	4 ОС
ОС1	0	0	0	0	0
БС1	2.15	1.21	1.01	1.23	1.1
БС2	17.97	1.35	1.18	0	5.68
БС3	51.2	1.49	1.55	6.88	7.92
БС4	31.02	1.21	1.04	8.09	4.34
БС5	70.62	1.25	0	1.64	0
БС6	16.34	1.14	0.98	2.1	1.58
БС7	63.1	1.71	1.02	2.02	1.24
БС8	27.48	1.28	0.98	2.28	1.89
БС9	9.52	1.2	0.96	1.65	1.32
БС10	14.72	1.19	1.04	3.32	2.2
БС11	80.5	0	0	0	0
БС12	12.47	1.18	1.08	1.03	0.95
БС13	2.53	1.26	1.03	2.21	2
БС14	48.2	0	0	0	0

Результирующая погрешность определения места i -й БС g i вычислялась следующим образом:

^ i = v c Xi +^ y . (5)

В таблице приведены результаты расчета погрешностей определения координат БС g i при выборе оптимального размещения станций по минимуму геометрического фактора их расстановки.

В данной таблице в первой колонке приведены названия станций в соответствии с обозначениями рисунка. Значения нулей, приведенные в строках значений погрешностей означают, что в данном режиме станция использовалась в качестве ОС и ее координаты не определялись.

Таким образом, полученные значения погрешностей показывают, что наиболее точным является дальномерный метод с выбором ОС из числа имеющихся станций по критерию минимума суммарного геометрического фактора остальных станций. Вместе с тем перед применением дальномерного метода целесообразно использовать угломерно-дальномерный метод для получения приблизительной оценки места всех станций. Затем необходимо выбрать из имеющихся станций, станции, назначаемые в качестве опорных (ОС1, ОС2, и т. д.) и осуществить определение координат данных станций с высокой точностью, после чего система переходит в штатный дальномерный режим определения координат объектов.

В случае необходимости обслуживания неограниченного числа объектов, либо при отсутствии возможности временной синхронизации сигналов всех станций, система может работать в разностнодальномерном режиме. В этом режиме сигналы излучают станции, выбранные в качестве ОС, а БС рабо- тают только в режиме пассивного приема сигналов. В данном методе уменьшение погрешностей достигается также за счет оптимизации выбора положения станций, назначаемых в качестве ОС по критерию минимума суммарного геометрического фактора для остальных станций, не назначенных ОС.

Исследованные методы определения относительных координат объектов могут найти применение в системах координатной привязки нескольких объектов относительно друг друга при выполнении транспортных перевозок, а также при разведке и добыче полезных ископаемых, где существует потребность в определении координат объектов, участвующих в проведении такого рода работ. В качестве прототипа таких систем может быть использована РНС «Крабик» выпускаемая серийно ОАО «НПП «Радиосвязь» г. Красноярска [3;14].