Исследование моделей электрической системы для определения расчетных предельных режимов

Режим электрической системы (ЭС) подвержен различного рода возмущениям: изменение нагрузки, генерации, состава оборудования, топологии сети и т.д. Поэтому при планировании, анализе и управлении режимами ЭС необходимо знать пределы с точки зрения устой- чивости и существования режимов.

В теории установившихся режимов (УР) предельный режим (ПР), как правило, ассоциируют с режимом, предельным по статической устойчивости. В настоящее время наиболее подробными для исследования устойчивости являются модели ЭС, использующие преобразования Парка-Горева. Довольно широкое распространение получила модель Парка-Горева 3-го порядка [1]. При добавлении к ней регулятора возбуждения и скорости турбины каждой синхронной машине (СМ) соответствует система уравнений (ПГ-модель):

T J d ^T - (M М - м Э t

^- К D ^to i) - ^(мМ ^{- (} X q ^- X' d )i d i q

^- E' q i q ^{- K}D ^ ^to )

;

‘ d 5       /     1)

— = to o (О) - 1 )

I dt dE`q

T d 0 ”~dT = ⁽E fd - E'q — ⁽X d - X ^ )i d ) = ⁽K A ^V 3 - ^V ) - ⁽X ^d - X' ^d )i ^d - E' ^ )

T R ^V = (U г - v)                                                            ⁽1)

dt

To  ,.М = (-Ko(o - °0 ) + ММ. -ММ ), dt                             0

где Ao - скорость перемещения ротора относительно синхронно вращающейся оси; Tj -постоянная механической инерции СМ; МЭ, ММ ‒ электрический и механический моменты; Xq , X'd - синхронное и переходное реактивные сопротивления по оси q(d); § - угол между ротором СМ и синхронно вращающейся осью; E`q ‒ ЭДС, пропорциональная потоку возбу- ждения СМ; T'd0 ‒ переходная постоянная времени по оси d; Efd ‒ ЭДС, пропорциональная напряжению обмотки возбуждения; v ,v3, Tr , Ka - управляющий сигнал, его заданное значение, постоянная времени и коэффициент усиления регулятора возбуждения; Uг ‒ модуль напряжения на шинах генератора; To, Ко - постоянная времени и коэффициент усиления регулятора скорости турбины.

Современные регуляторы имеют высокий коэффициент усиления (200-400 ед.) и малую постоянную времени, что позволяет при выполнении практических расчетов считать Ka = ю и Tr = 0. В этом случае третье уравнение системы (1) приводится к следующему виду: AUг = Uг -v3 = 0 [2]. Если, кроме того, принять постоянство механического момента турбины, отсутствие демпферных моментов ( Kd = 0) и малые отклонения частоты ( о « ®о), можно получить классическую позиционную модель ЭС (П-модель):

Tj-- = AP(§§H ,Vh ) dt                          ,

0 = AP,Qh (д§н ,Vh )

где A P( 6 , § н ,V h ) - вектор небалансов мощности на валу СМ; A P,Q h ( 6 , § н ,V h ) - векторы небаланса активной и реактивной мощности в узлах нагрузки; § н , У ц - векторы углов и модулей напряжения нагрузочных узлов.

В практике расчетов большее распространение получила модель с шинами неограниченной мощности (НМ-модель). Эта модель использует систему уравнений (2) с той лишь разницей, что в одном из узлов полагается Tr =да и, следовательно, dAcoJdt = 0. При этом размерность системы (2) уменьшается на единицу, поскольку напряжение шины бесконечной мощности полагается неизменным по абсолютной величине и фазе при любых условиях работы ЭС. В этом случае при соответствующем задании исходных данных свободный член характеристического уравнения НМ-модели представляет собой матрицу Якоби уравнений УР. Это позволяет использовать модель УР для расчета предельных по апериодической статической устойчивости режимов ЭС [2].

Целью работы является исследование модели Парка-Горева 3-го порядка, дополненной уравнениями регуляторов возбуждения и скорости турбины, позиционной модели и модели с шинами неограниченной мощности, и выбор моделей, которые больше подходят для определения расчетных ПР на примере кольцевой трехмашинной системы, представленной в приложении.

Модель Парка-Горева

Совокупность всех УР ЭС, в том числе гипотетических (неустойчивых), представляет собой гиперповерхность мощностей УР ЭС (ГПМ) [3]. Каждый УР ЭС соответствует определенной точке ГПМ, и наоборот. ГПМ исследуемой трехузловой ЭС представлена на рисун-

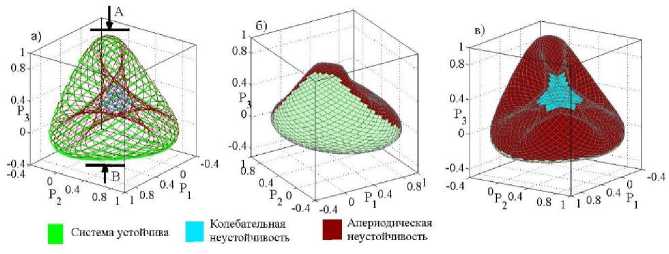
Рисунок 1 ‒ Гиперповерхность мощностей в 3-узловой ЭС

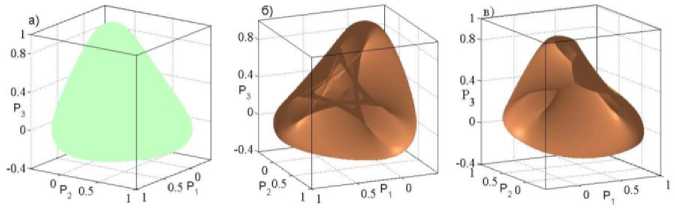
Рисунок 2 ‒ Устойчивая (а) и неустойчивая (б-в) части гиперповерхности мощностей ке 1. ГПМ имеет достаточно сложную структуру даже для простых систем. На рисунке 2 а отдельно показана часть ГПМ статически устойчивых УР, а на рисунке 2 б, в с двух сторон представлена часть ГПМ статически неустойчивых УР ЭС.

Согласно рисунку 2 б, в область ГПМ статически неустойчивых УР имеет сложный рельеф. Особенно это касается области шестиугольника, в которой мощности всех узлов положительны ‒ вся генерация идет только на покрытие потерь в сети. В то же время область ГПМ статически устойчивых УР имеет простую, довольно «гладкую» форму, которую можно легко визуализировать, проектируя ГПМ вдоль направления оси активной мощности одного из узлов на подпространство (плоскость) мощностей двух других узлов. Такая проекция называется областью существования УР ЭС.

На рисунке 3 представлены области статической устойчивости ПГ-модели при различных соотношениях между коэффициентами усиления регуляторов скорости турбин. Рисунок 3 а-г соответствует виду сверху (направление А рис. 1), а рисунок 3 д-з ‒ виду снизу (направление B рис. 1). Зеленым цветом обозначена область устойчивой работы, синим – область колебательной неустойчивости, красным – апериодической неустойчивости. При увеличении одного из коэффициентов усиления K _{ω i} область статической устойчивости изменя-

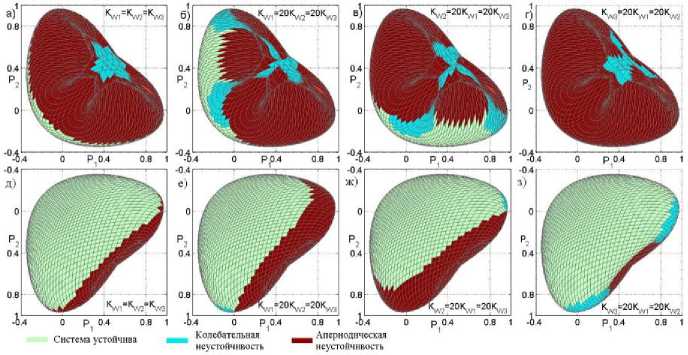
Рисунок 3 ‒ Влияние коэффициентов усиления регуляторов турбины на устойчивость ПГ-модели ется. Она уменьшается на «нижней» части ГПМ на рисунке 2 е-ж и увеличивается на ее верхней стороне (рис. 3 б-в). Там же появляются дополнительные области колебательной неустойчивости. Для рисунка 3 г-з наблюдается обратная картина.

На рисунке 4 представлены области статической устойчивости ПГ-модели при различных соотношениях между T J_i . Варьирование постоянных инерций не изменяет границу апериодически устойчивых режимов. Этого следовало ожидать, так как постоянные инерции не входят в свободный член характеристического уравнения ПГ-модели. В то же время увеличение T _Ji приводит к уменьшению области статической устойчивости за счет появления дополнительной области колебательной неустойчивости (см. рис. 4 е-з, б-г ). Области статической устойчивости на нижней части ГПМ (см. рис. 4 е-з ) достаточно близки к случаю варьирования K _{ω i} , однако на верхней части ГПМ область статической устойчивости не увеличивается (рис. 4 а-г ).

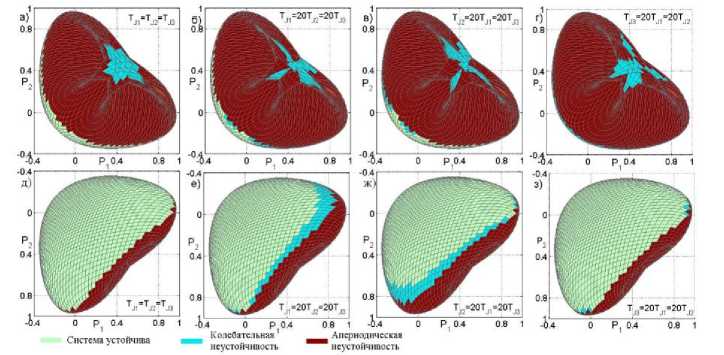
Рисунок 4 ‒ Влияние постоянных механической инерции на устойчивость ПГ-модели

Позиционная модель

На рисунке 5 представлены области статической устойчивости П-модели при различных соотношениях между постоянными механической инерции. Увеличение одной из постоянных механической инерции приводит к изменениям границы области апериодической статической устойчивости подобным изменениям области устойчивости ПГ-модели при варьировании K _ω i . Согласно рисункам 3, 5 П-модель при этом характеризуется меньшей областью статической устойчивости по сравнению с ПГ-моделью за счет большей области колебательной неустойчивости. Это объясняется наличием в ПГ-модели коэффициента демпфирования и действием регуляторов, которые не учитываются в П-модели.

Модель с шинами неограниченной мощности

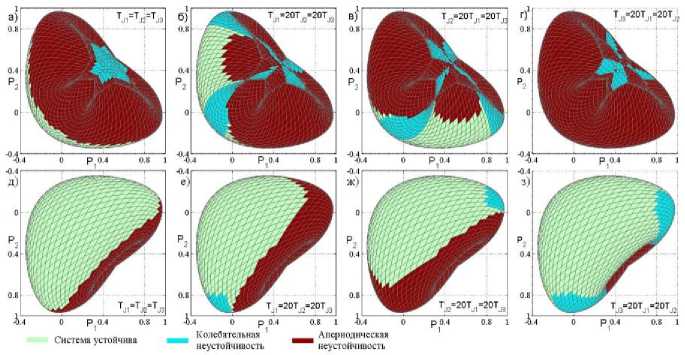
Рисунок 5 ‒ Влияние постоянных механической инерции на устойчивость П-модели

В качестве шин неограниченной мощности в НМ-модели обычно принимается наиболее мощная станция ЭС. В рассматриваемой системе параметры всех генераторов одинаковы, и в качестве шин неограниченной мощности, которые соответствуют балансирующему узлу (БУ) в модели потокораспределения, может быть принят любой узел. На рисунке 6 представлены области статической устойчивости НМ-модели при различном расположении шин неограниченной мощности. Рисунок позволяет проиллюстрировать интересную особенность НМ-модели – зависимость рассчитываемых ПР от месторасположения БУ [4]. Например, при Р 2 =0,4 о.е. предел по статической устойчивости при первом балансирующем узле наступит при Р 1 =0,3172 , Р 3 =-0,348 , при втором балансирующем узле ‒ при Р 1 =0,2825 , Р 3 =-0,3486 , а при третьем ‒ при Р 1 =0,5709 , Р 3 =-0,1101 о.е.

Сравнивая рисунок 6 с рисунками 3 и 5 можно отметить, что области статической устойчивости НМ-модели с шинами неограниченной мощности в i-ном узле, практически совпадают

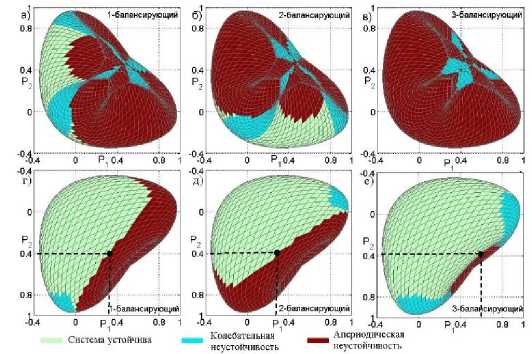
Рисунок 6 ‒ Влияние месторасположения балансирующего узла на ПР НМ-модели с областями устойчивости П-модели со значительно увеличенной постоянной механической инерции i-ного узла и ПГ-модели со значительно увеличенным коэффициентом усиления регулятора турбины. Это означает, что при выполнении сделанных допущений – правильной настройке регуляторов и выборе в системе балансирующей точки (в качестве которой обычно принимают станцию, осуществляющую частотное регулирование, либо наиболее мощную станцию энергосистемы), НМ-модель дает адекватные результаты при выполнении практических расчетов нахождения предельных по апериодической статической устойчивости УР ЭС. С другой стороны, если выбор БУ будет произведен без учета специфики ЭС, не будет соответствовать реальному соотношению постоянных механической инерции и коэффициентов усиления регуляторов скорости турбины, то использование НМ-модели приведет к неверной оценке ряда предельных по статической устойчивости режимов ЭС.

Сравнительный анализ моделей

В ПР НМ-модели относительный прирост потерь (ОПП)* ∂π ∂P для БУ равен единице [5]. То есть любые попытки БУ поддержать УР в ПР полностью блокируются возникающими при этом потерями активной мощности. Неспособность БУ поддержать УР даже ряда узлов определяет ПР ЭС. Рассмотрим, например, режим в точке А на рисунке 7, где область с ОПП меньше единицы для всех узлов выделена на ГПМ НМ-модели. В этом режиме ОПП для первого узла (при БУ во 2 или 3 узле) равен 1, а для 2 и 3 узлов – меньше единицы. Поэтому если БУ будет назначен 1 узел, то этот режим будет ПР. Однако режим не останется ПР, если БУ будет перемещен во 2 и 3 узлы, поскольку их ОПП меньше 1 и имеется возможность дальнейшей загрузки генераторов.

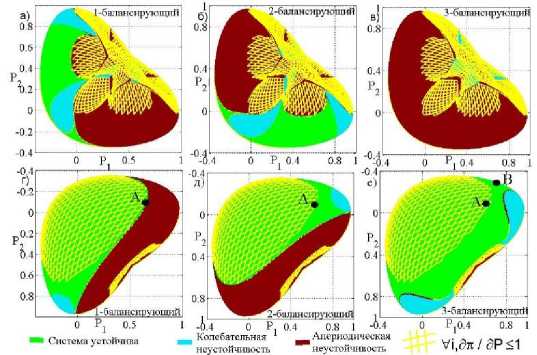
Рисунок 7 ‒ Области относительных приростов потерь ∂ π ∂ P ≤1

Согласно рисунку 7, среди ПР НМ-модели существуют режимы, в которых ОПП какого-либо узла превышает единицу. Нагрузка в таких режимах получается меньше максимально возможной, поскольку простым снижением генерации в узле с ∂ π ∂ P >  1 можно добиться повышения мощности нагрузки (потери будут снижаться быстрее, чем мощность, вырабатываемая в i-ном узле). Рассмотрим, например, режим в области с ∂ π ∂ P >  1 в точке B, который характеризуется мощностями Р 1 =0,753, Р₂=-0,277, Р_з=0,05 (Р р =0,758, Р_Н=0,277). Нагрузка в этом режиме получается меньше, чем, например, в режиме в точке A, находящемся на границе области дПд р <  1 , V i (Р 1 =0,672, Р 2 =-0,103, Р з =-0,235, Р г =0,672, Р н =0,338).

П- и ПГ-модели, фактически, в неявном виде также используют БУ, а именно распределенный балансирующий узел, при котором небаланс системы распределяется между узлами в соответствии с коэффициентами участия αi . Действительно, в ПГ-модели при наличии регуляторов скорости турбины небаланс распределяется между машинами в соответствии с их частотными характеристиками ΔPi = KωiΔfi [5]. Суммируя эти уравнения для всех СМ и учитывая равенство частоты в системе, без труда можно получить Δf = ∑ΔP ∑K , где ∑ΔP представляет собой общий небаланс системы. Тогда небаланс, покрываемый i-ной машиной, равен ΔP = ΔP K ∑K . Небаланс системы в П-модели после кратковременного переходного процесса распределяется между СМ в соответствии с их постоянными механической инерции [5]. Для того чтобы убедиться в этом, достаточно рассмотреть уравнения П-модели (2). Суммирование уравнений для всех СМ дает ∑TJi d2δi dt2=∑ΔPi = ΔPЭС . Известно, что после кратковременного переходного процесса все СМ в ПМ будут иметь одно и то же ускорение d 2δЭС dt2= ΔPЭС ∑ TJi . Подставив это значение в уравнение для i-ной машины, легко получить небаланс, покрываемый этой машиной: ΔPi = ΔPЭС TJi ∑ TJi . Таким образом, коэффициенты участия в распределенном БУ в П-модели пропорциональны постоянным инерции СМ TJi , а в ПГ-модели – пропорциональны Kωi . Предельному по апериодически статиче- ской устойчивости режиму с распределенным БУ отвечает условие

^ а / 1-д П д P i ) = 0 [6].

Коэффициенты участия узлов а в распределенном БУ положительны, следовательно, в ПР П- и ПГ-моделей ОПП некоторых узлов превышает единицу. Поэтому в ПР этих моделей нагрузка ЭС получается меньше максимально возможной (ср. рис. 3-6 с рис. 7).

Согласно методическим указаниям по устойчивости ЭС, коэффициент запаса по активной мощности определяется через предельные по статической апериодической устойчивости перетоки мощности в сечении [7]. При этом не уточняется, с какой стороны должен определяться переток, с передающей или принимающей. Эти перетоки совпадают лишь в консервативной ЭС, т.е. при отсутствии активных сопротивлений. При нахождении максимально допустимого перетока в сечении с помощью НМ-модели траектория утяжеления может быть такой, что ряд узлов будет иметь ОПП больше единицы в ПР (см. рис. 7). То есть в этом ПР нагрузка ЭС получается меньше максимально возможной для заданной траектории утяжеления. Назначением ЭС является надежное обеспечение нагрузки, а не чрезмерная загрузка генераторов, которая получается в этом случае. Кроме этого такие ПР (с ОПП больше единицы) могут быть статически неустойчивым (см. рис. 2-7). Между тем, согласно рисунку 7, нижняя область ГПМ с ОПП д п/ д Р ^ <  1 , Vi является как апериодически, так и колебательно, статической устойчивой, а УР на границе этой области соответствуют максимально возможным нагрузкам ЭС в заданных направлениях утяжеления.

Поэтому в качестве расчетной больше подходит НМ-модель, в ПР которой ОПП для всех узлов не превышают единицу. Для реализации такой модели существующие блоки утяжеления следует дополнить проверкой ОПП. Если на каком-то шаге утяжеления окажется, что ОПП какого-либо узла превышает единицу, этот узел следует переназначить балансирующим. Найденный таким образом ПР определит максимальную величину нагрузки ЭС для заданной траектории утяжеления и будет статически устойчивым.

Выводы

В предельных по статической устойчивости режимах позиционной модели и модели Парка-Горева относительные приросты потерь некоторых узлов превышают единицу. Нагрузка энергосистемы в этих предельных режимах получается меньше максимально возможной – снижение генерации в узлах с относительными приростами потерь больше единицы приводит к увеличению полезно отдаваемой мощности. В предельных режимах модели с шинами неограниченной мощности часть узлов также может иметь относительные приросты потерь больше единицы. Кроме того, такие предельные режимы НМ-модели и установившиеся режимы в его окрестности могут быть статически неустойчивыми.

Нижняя область гиперповерхности мощностей с относительными приростами потерь меньше 1 для всех узлов является статически устойчивой. Установившиеся режимы на границе этой области соответствуют максимально возможным нагрузкам ЭС для заданных направлений утяжеления. Назначением ЭС является надежное обеспечение нагрузки, а не чрезмерная загрузка генераторов. Поэтому для определения расчетных предельных режимов более подходящей является модель с шинами неограниченной мощности, в предельных режимах которой относительные приросты потерь всех узлов не превышают единицу. Для реализации такой расчетной модели существующие блоки утяжеления следует дополнить проверкой относительных приростов потерь. Если на шаге утяжеления окажется, что для какого-то узла относительный прирост потерь превысил единицу, то этот узел следует переназначить балансирующим. Найденный таким образом предельный режим будет статически устойчивым и определит наибольшую величину нагрузки энергосистемы для заданной траектории утяжеления.

Приложение

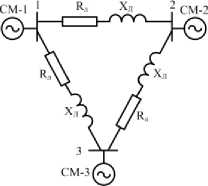
СМ - ТГВ-60: Р _ном = 60 МВт, cos ф = 0,85, f_H o _M= 50 Гц, U hom =10,5 кВ, X d =X q = 1,66 о.е., х _л 0,12 о.е., r= 0,002 о.е., T' _d 0 = 6 с., T j =12,37 с., K A = 200 , T r =0,02 с., I, . 0,5 с., К _ю = 20 Линия АС120/19 мм²: R л =1,4234 о.е., Х Л =2,6763 о.е.

Рисунок ‒ Трехмашинная система