Исследование модельной задачи структурной биоинформатики

Белки – это цепочки аминокислотных остатков, соединённых пептидной связью. В их строении участвуют преимущественно 20 стандартных аминокислот. Одним из этапов синтеза белка является молекулярный биологический процесс под названием трансляция, в результате которого образуется одномерная полипептидная цепь (первичная структура). Аминокислоты в ней начинают взаимодействовать друг с другом, в результате чего цепь сворачивается в уникальную объёмную структуру. Механизмы этого сворачивания (или фолдинга) плохо изучены и не могут быть качественно промоделированы. Однако информация о трехмерной структуре белка крайне важна, так как она позволяет определить функцию этого белка [1].

В результате современных широкомасштабных работ по исследованию ДНК, таких как проект «Геном человека», на сегодняшний день доступны огромные объёмы данных о первичных структурах. GenBank – крупнейшая база нуклеотидных и белковых последовательностей – содержит более 200 миллионов полипептидных цепей. Пространственные структуры известны всего лишь для 150 тысяч из них [2] (по состоянию на апрель 2020 года). Нахождение трехмерных структур белков экспериментальным путём трудоёмко и экономически не целесообразно.

Известно, что искомая пространственная структура имеет минимально возможную потенциальную энергию [3]. В связи с этим проблему фолдинга можно рассматривать как класс задач глобальной оптимизации. Их характерным свойством является высокая размерность и, как следствие, длительное время вычисления функции энергии. Также важно заметить, что число всевозможных конфигураций зависит от длины цепи экспоненциально. Даже для небольшого белка время работы алгоритма полного перебора превысило бы время существования вселенной. Поэтому в вычислительной биологии используются подходы, производящие поиск решений наиболее эффективно в плане количества вычислений функции энергии [4]. Существуют две стратегии: статистические методы и физические методы (методы De novo ).

Примером статистического метода является сопоставительное моделирование (или моделирование на основании гомологии, homology modeling). Метод заключается в поиске среди последовательностей, для которых уже известна пространственная структура, гомологичных (или идентичных) последовательности моделируемого белка. Исходя из предположения, что белок будет иметь подобную структуру, производят построение моделей белка для гомологичных последовательностей. Только после этого вычисляют энергию, проводят оптимизацию составленных структур, выбирают наиболее удачную в качестве результата. В случае, если в базе не удалось найти гомологичные бел- ковые последовательности, моделируемый белок «нарезают» (threading, fold recognition), производят процедуру для отдельных частей, а в конце оптимизируют структуру целиком.

Однако статистические методы не могут претендовать на универсальность. Поэтому для прогнозирования структуры белка предпочтительнее использовать методы De novo , то есть напрямую по первичной структуре, без использования каких-либо явных шаблонов. Установлено, что информации только лишь о первичной структуре должно быть достаточно для получения точного решения [3]. Крупнейший в мире проект добровольных вычислений, направленный на решение проблемы фолдинга, Rosetta@Home использует такие методы [5]. Дальнейшее развитие методов De novo остаётся весьма актуальным.

Как уже было отмечено, функция энергии белковой структуры обладает высокой вычислительной сложностью. Проводить исследования и адаптацию методов на оригинальных задачах было бы крайне неудобно из-за огромных временных затрат. В связи с этим было принято решение делать это на упрощенных модельных задачах укладки графа, сохраняющих характерные свойства исходных задач. Мы полагаем, что вводимые упрощения будут допустимы, если для последовательностей элементов аналогичных аминокислотным остаткам (имеющих аналогичные численные характеристики) решением модельной задачи будет подобная структура. Подобные идеи используются при крупнозернистом моделировании [6].

Целями настоящей работы являются:

• -    формализовать класс модельных задач укладки графа;

• -    исследовать существующие эволюционные алгоритмы и используемые в них подходы, выделить среди них пригодные для решения поставленной модельной задачи;

• -    реализовать выбранные алгоритмы и универсальную систему их тестирования;

• -    выполнить численное исследование работы рассматриваемых алгоритмов на вычислительном комплексе IBM Polus факультета ВМК МГУ.

Модельная задача

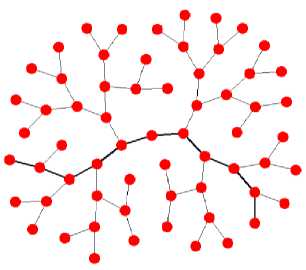
Пусть дан связный ациклический граф G = (V, Е) на плоскости (дерево), все вершины которого имеют одинаковый набор свойств (числовых характеристик), а все рёбра имеют одинаковую фиксированную длину. В наших исследованиях мы ограничивались двумя свойствами - условными «массой» и «зарядом» вершин, отвечающими за их взаимное притягивание и отталкивание. Каждая вершина дерева кроме корневой имеет одну и только одну родительскую, с которой соединена (входным) ребром. Таким образом, если считать фиксированными положения двух первых вершин основной цепочки, любую пространственную структуру (конфигурацию) графа можно представить п = |Е| - 2 параметрами X i , Х 2 , ..., Х п , где X t - угол между входным ребром i -й вершины и входным ребром ее родительской вершины (рис. 1). Также пусть задана некоторая функция энергии F(x i , X 2 , ^, Х п ) заданной укладки графа, минимум которой и требуется найти.

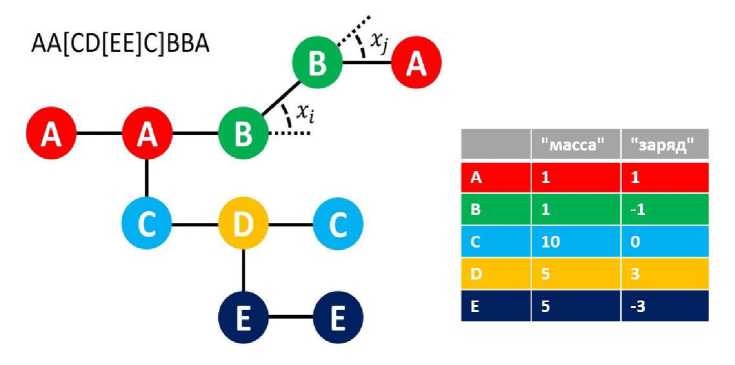
Рис. 1. Пример укладки графа, заданного строкой AA[CD[EE]C]BBA

Граф G - это входные данные конкретной модельной задачи. Для проведения в дальнейшем вычислительных экспериментов было необходимо продумать формат представления этих данных. В качестве такого формата можно использовать специальное строковое представление. Пусть имеется алфавит символов, каждому из которому сопоставлены значения свойств вершин («масса» и «заряд»). Тогда строка из таких символов задаёт на плоскости линейный граф (цепочку) из последовательно соединённых рёбрами вершин, каждой из которых соответствует символ строки. Если после некоторого символа (кроме самого первого) участок строки заключён в квадратные скобки, будем считать, что эта подстрока задаёт подграф для вершины, соответствующий этому символу (то есть существует ребро между ней и корневой вершиной подграфа, см. пример на рис. 1). Значения свойств каждой вершины определяются соответствующим ей символом. В такой формулировке символы представляют из себя аналоги аминокислотных остатков, из которых состоят полипептидные цепи.

Функцию энергии белковой молекулы находят как сумму атомных взаимодействий в ней [5].

Аналогичным образом зададим нашу целевую функцию F:

Z ( mass(u) mass(v)

charge(u) charge(v) r(u, v)B

")'

(a-----7---77----+ 3

\       r(u, v)A u,v е v           х    , u^v где r(u,v) - расстояние между вершинами u и v, a, (, А, В - вещественные коэффициенты. Из формулы видно, что функция F разрывна в точках, когда некоторые вершины занимают одно и то же положение в пространстве и расстояние между ними становится нулевым. В настоящих белковых структурах такие конфигурации физически невозможны. В связи с этим для вершин, расстояние между которыми меньше некоторого фиксированного числа /, вместо соответствующего слагаемого в

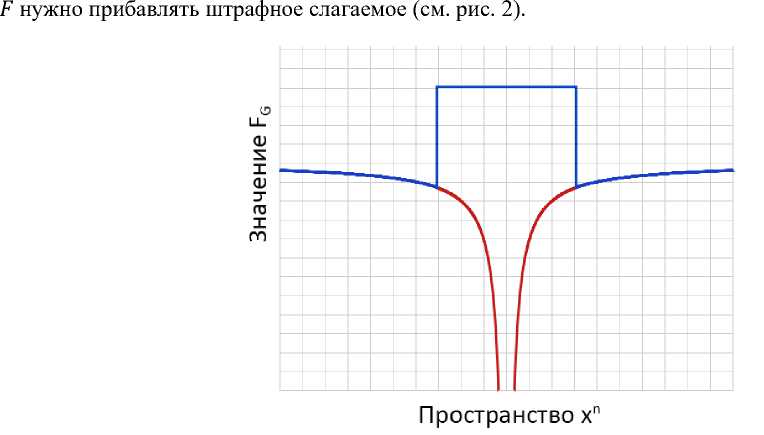
Рис. 2. Поведение функции энергии F без штрафа (красный) и со штрафом (синий)

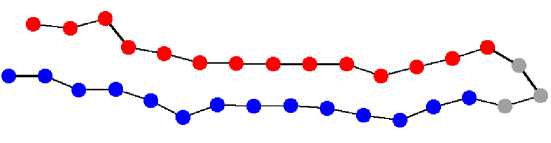
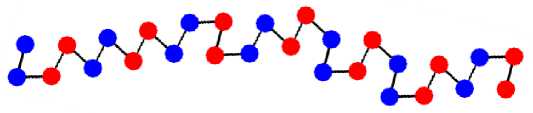
Конкретные параметры для вычисления функции энергии подбирались уже с использованием программной реализации экспериментально. Брались графы разной длины аналогичные альфа-листам и бета-спиралям (вторичным структурам, см. рис. 3) - наиболее распространённым локальным структурам в белковых молекулах [4]. Для них вручную задавалась углы для подобных конфигураций на плоскости, которые должны быть правильными решениями модельных задач. Затем запускался простейший алгоритм, который случайным образом немного изменял эти углы. Если в этом или последующих вычислительных экспериментах обнаруживалась конфигурация с меньшей энергией, параметры функции энергии корректировались эмпирически, основываясь на особенностях этой конфигурации.

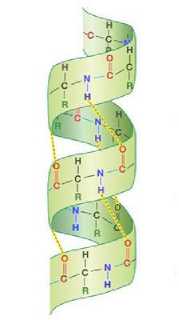
Рис. 3. Альфа-спираль (слева) и бета-лист (справа)

Алгоритмы оптимизации

Наиболее развитый класс эволюционных алгоритмов оптимизации - это генетические алгоритмы (ГА, genetic algorithm , GA ). Кроме того, популярным эволюционным алгоритмом является алгоритм дифференциальной эволюции (ДЭ, differential evolution, DE). И генетические алгоритмы и алгоритм дифференциальной эволюции показывают хорошие результаты для широкого спектра задач, не требуют тщательной настройки параметров для каждого конкретного графа, а также обладают хорошим потенциалом для параллельной реализации [7]. В настоящей работе использовались классические версии указанных алгоритмов со стандартными значениями их параметров.

Очевидно, что даже простой многократный запуск эволюционного алгоритма оптимизации повышает вероятность нахождения глобального экстремума. В островной модели ( island model ) алгоритм работает параллельно на нескольких узлах вычислительной системы, а также осуществляет обмен решениями между ними. Для этого вся популяция разбивается на некоторое число субпопуляций, каждая из которых помещается на отдельный узел. Затем субпопуляции эволюционируют под действием операторов эволюционного алгоритма. Раз в несколько поколений на узлах синхронно применяется оператор миграции. Этот оператор производит обмен части субпопуляций между соседними вычислительными узлами (у которых есть прямая связь).

В клеточных эволюционных алгоритмах ( cellular evolutionary algorithm, cEA ) популяции организованы сетками, каждое решение имеет свою фиксированную клетку в них. Это позволяет накладывать ограничения на выбор пары для совместных операторов. Например, в качестве пар для отбора турнирным методом можно выбирать только решения в соседних клетках. Благодаря этому, решения, расположенные в разных частях сетки, оказываются изолированными друг от друга, что способствует сохранению разнообразия в популяции. Для клеточных алгоритмов тоже вводят оператор миграции. В этой модели решения мигрируют в соседние клетки. Также в клеточных алгоритмах возможно задавать неоднородные параметры, зависящие от положения в сетке [8]. Например, у краёв сетки параметр мутации можно установить высоким, а в центре почти нулевым. В параллельной версии клеточного алгоритма части сетки размещены на разных вычислительных узлах. Для эффективных коммуникаций соседние части сетки должны находится на узлах, между которыми есть прямая связь.

Программная реализация

Вариативность исследуемых алгоритмов предопределила необходимость разработки программного комплекса для анализа алгоритмов непрерывной оптимизации для решения задачи укладки графа на плоскости. К тестирующей системе были поставлены следующие требования:

• -    возможность тестирования алгоритмов, оперирующих только функцией энергии и не учитывающих фактическое представления графа;

• -    универсальный способ передачи параметров алгоритмов;

• -    автоматический сбор статистики при выполнении алгоритмов;

• -    визуализация получаемых результатов;

• -    структурированное хранение всех полученных результатов.

Реализованная система может использоваться удалённо через простой пользовательский вебинтерфейс. Также возможно взаимодействие через интерфейс командной строки. Тестируемые алгоритмы описываются на языке C++, возможно с применением технологии Message Passing Interface ( MPI ). На странице загрузки upload . php (рис. 4) пользователь вводит код алгоритма, имя теста, прописывает используемые в нём параметры и их значения, выбирает граф для тестирования и загружает эту информацию в систему.

• 4- С ® Lesl.ru Загрузка алгоритма                                                                                                                               ■    ... Ф

Загрузка алгоритма

Имя: GA by Andrey einclude void eueste(Task 4т, double ••₽, int ■, int n)

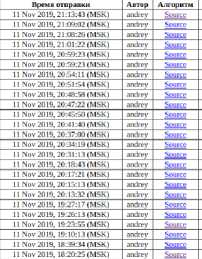
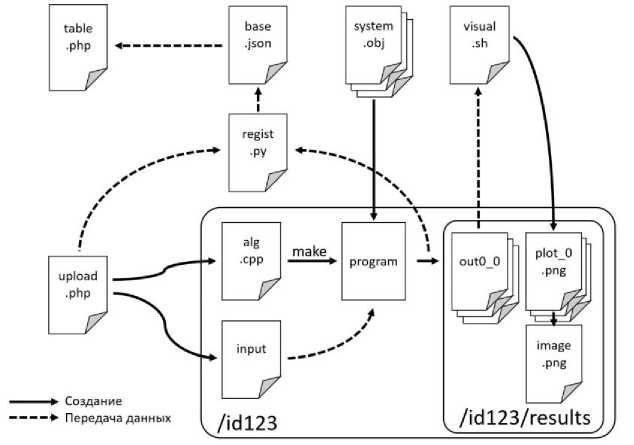
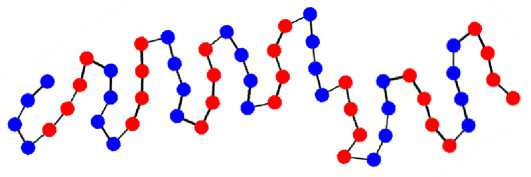
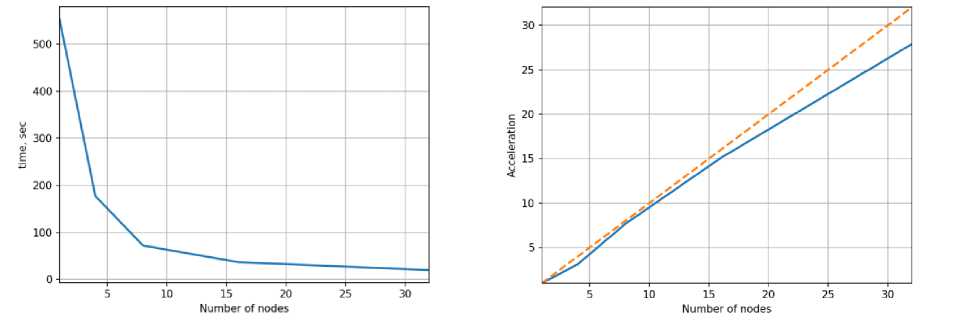
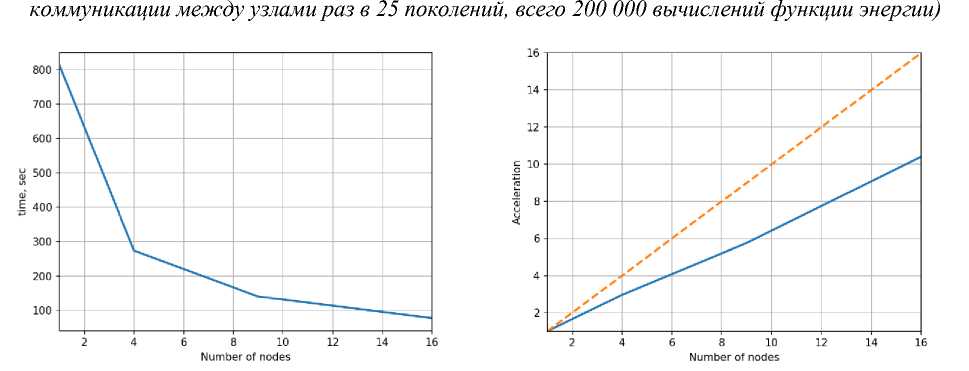
double «rate - T[-wtete_rete’'J; foe (int i - e; i < e; *♦!) { for

Рис. 4. Страница upload. php

Система несколько раз запускает алгоритм на всех доступных ей вычислительных узлах. Результатом работы является директория, содержащая текстовые файлы формата out_. Эти файлы содержат в каждой строке номер популяции, среднее значение функции энергии, лучшее решение и значение функции энергии для него. Затем для проведённых запусков строятся графики средних значений функции энергии по поколениям для всех узлов. Для узла, на котором было достигнуто минимальное значение функции энергии, происходит визуализация результатов.

<- C @ testru Посылки

Посылки

andrey andrey andrey

AAAAAAAACCEEEEEEEE AAAAAAAACCEEEEEEEE AAAAAAAACCEEEEEEEE

AAAAAAAAAA

AAAAAAAAAA

AAEEAAEEAAEEAAEEAAEEAAEE AAEEAAEEAAEEAAEEAAEEAAEE AAEEAAEEAAEEAAEEAAEEAAEE AAEEAAEEAAEEAAE EAAEEAAEE AAEEAAEEAAEEAAEEAAEEAAEE AAEEAAEEAAEEAAEEAAEEAAEE AAEEAAEEAAEEAAEEAAEEAAEE AAEEAAEEAAEEAAEEAAEEAAEE

A| b JA( b |E[b]E|b|A[b] A[b]E, b]E[bJA [b] A |b]E[b)E[b| Alb I А|Ъ 1Е1ЫЕ1ЫА1ЫА1ЫЕ1ЫЕ1ЫА |b IА1ЫЕ1ЫЕГЫ

A[b]A|bJE[b]E[b]A[b]A[b]E[b]E[b]A[b]A[b]E[b)E[b]

A[b]A(b]E(b]E[b]A[b]A[b]E[b]E[b]A[b]A(b]E[b]E[b]

AAAAAAAACCEEEEEEEE

A|b]A|b|E|b]E|b|A[b]A[b|E[b]E|b|A|b]A|b]E[b)E[b] A[b]A(b]E[b]E[b]A[b]A[b]E[b]E[bJA[bJA[b]E[b)Elb] A[b J A[b |E|bJE|bJA[b] A[b]E[ b]E[bJA |bjA[b]E[b]E[b]

AAAAAAAAAA

AAAAAAAAAA

A[b]A(b]E[b]E[b]A[b]A[bJE[b]E[b]A[b]A[b]E[b)E[b]

График PNG GIF

График PNG GIF

График PNG GIF

График PNG GIF

Визуализация

График PNG GIF

J-рафик PNG GIF График PNG GIF График PNG GIF График PNG GIF 1фафик PNG GIF График PNG GIF

Гфафик PNG GIF График PNG GIF График PNG GIF График PNG GIF График PNG GIF График PNG GIF

Compilation erroi

Compilation error

Принцип работы системы схематично проиллюстрирован на рис. 6. Для каждого запуска выделяется уникальный идентификатор (номер) и создаётся отдельная директория. В ней создаётся файл alg.cpp с кодом алгоритма, а также специальный конфигурационный файл input с параметрами алгоритма и информацией о самой задаче (тестовый граф, параметры функции энергии). После этого

вызывается утилита make, которая компилирует объектный файл и производит его линковку с объектными файлами тестирующей системы. Полученная программа запускается и получает на вход конфигурационный файл input.

Рис. 6. Схема функционирования модуля «Добавление данных»

После успешного завершения программы выполняется сценарий, вызывающий python-программы для отрисовки графиков и изображений по полученным данным в директории results. После каждого этапа работы, а также при возникновении каких-либо ошибок, python-программа regist.py регистрирует информацию в файле base.json, который отображается пользователю на странице table.php. Помимо прочего, в base.json хранятся имена и время загрузки для всех тестов.

Численные эксперименты

Для проведения вычислительных экспериментов тестовая система была установлена на вычислительном комплексе IBM Polus факультета ВМК МГУ. С целью первичной проверки работоспособности предложенных методов, алгоритмы были протестированы на полных двоичных деревьях с вершинами с одинаковым зарядом. Для них всех удалось получить структуры, в которых нет пересечений рёбер, а расстояние между близко расположенными вершинами приблизительно одинаково (см. рис. 7).

Рис. 7. Пример укладки полного двоичного дерева высоты 6

Все дальнейшие численные эксперименты проводились на графах, аналогичных альфа-спиралям, бета-листам и их комбинациям (см. рис. 8). В введённом выше строковом представлении эти графы имеют формат А^пС^тВ^п (при т«п), (ААВВ)^п и (А^пВ^п)^т соответственно (запись Х^к обозначает повторение строки X к раз), где А - лёгкие вершины с положительным зарядом, В - такие же, но с противоположным по знаку зарядом, С - тяжёлые вершины с нейтральным зарядом.

Рис. 8. Примеры укладки трех типов графов, на которых проводились численные эксперименты

Целями проведения вычислительных экспериментов была настройка параметров исследуемых алгоритмов оптимизации, а также сравнение эффективности различных вариаций генетического алгоритма и алгоритма дифференциальной эволюции. Эксперименты показали, что бета-листы -более простые структуры, чем альфа-спирали. Для небольших графов с их нахождением так или иначе справляются все вариации рассматриваемых алгоритмов. С ростом числа вершин последовательные алгоритм дифференциальной эволюции и генетический алгоритм сходятся к худшим реше- ниям, параллельные же версии продолжают показывать неплохие результаты.

Алгоритмы дифференциальной эволюции (с островной моделью и с оператором мутации) находят альфа-спирали лучше генетических. Но даже у них в структурах часто неверно повёрнуты рёбра на локальных сегментах. Скорее всего для решения этой проблемы необходимо усложнять модель. Для длинных графов ни один алгоритм не показал удовлетворительных результатов в полной мере. Однако алгоритм дифференциальной эволюции с оператором миграции и клеточный алгоритм с неоднородным параметром мутации находят наилучшие структуры, выстраивая наиболее длинные спирали в локальных областях. Это справедливо и для более сложных структур, являющихся комбинацией альфа-спиралей и бета-листов.

Также был проведён анализ эффективности работы параллельных алгоритмов (рис. 9 и 10). В островной модели коммуникации между процессами происходят редко, поэтому её ускорение намного лучше, чем у клеточного алгоритма, в котором коммуникации происходят на каждой итерации.

Рис. 9. Время работы и ускорение островной модели (граф из 100 вершин, размер субпопуляций – 50,

Рис. 10. Время работы и ускорение клеточного алгоритма (граф из 100 вершин, размер сетки 12x12, всего 200 000 вычислений функции энергии)

Заключение

В результате выполненной работы были получены следующие результаты:

• -    в результате проведённого обзора силовых алгоритмов визуализации графов и эволюционных алгоритмов, изучения теоретического обоснования и принципов их работы отобраны алгоритмы для тестирования;

• -    для проведения вычислительных экспериментов разработана система тестирования последовательных и параллельных алгоритмов решения задачи укладки графа на плоскости;

• -    в рамках этой системы выполнена реализация нескольких последовательных и параллельных эволюционных алгоритмов с использованием технологии MPI;

• -    анализ результатов проведенных вычислительных экспериментов показал, что наилучшую сходимость к качественному решению для наиболее широкого класса структур имеют гибрид алгоритма дифференциальной эволюции с островной моделью и клеточный алгоритм с неоднородным параметром мутации.