Исследование наноструктурированных материалов

Макроскопические свойства материалов, такие, как электропроводность, теплопроводность, прочность, радиационная стойкость и морозостойкость, во многом обуславливаются структурами с характерными размерами от единиц до сотен нанометров (наноструктур). В этом диапазоне находятся размеры неоднородностей различной физической природы в кристаллизующихся полимерах [1], размеры мицелл в лиотропных жидких кристаллах [2], размеры доменов в блок-сополимерах [3] и функциональных элементов биологических объектов [4]. В этом же диапазоне, по-видимому, находится предел возможной миниатюризации электроники [5]. Этот далеко не полный перечень дает краткое представление об актуальности исследований наноструктур. Особенно актуально исследование наноструктур с целью создания новых материалов для различных наукоемких технологий.

ВЕСТНИК 2016

Очень холодные нейтроны (ОХН) рассеиваются и поглощаются ядрами атомов. Сечения поглощения таких нейтронов существенно ниже, чем рентгеновских лучей. Это даёт возможность успешно проводить исследования наноструктур массивных образцов. Наличие у нейтрона магнитного момента позволяет исследовать распределение спиновой плотности в этих образцах. В начале статьи даётся описание метода рассеяния ОХН и времяпролётного спектрометра ОХН [6]. Далее рассмотрены модели различных сред. Для каждой из моделей получены макроскопические сечения упругого рассеяния ОХН. В заключении выполнено краткое сравнение различных методов исследования наноструктурированных материалов.

Метод рассеяния очень холодных нейтронов

Энергия очень холодных нейтронов 2,5 · 10 ^–7 < <  Е < 5 · 10 ^–7 эВ много меньше энергии химических связей, существующих между атомами. Поэтому рассеяние ОХН на неоднородностях наноструктур не изменяет состояния рассеивателя. Процесс взаимодействия ОХН с исследуемым образцом сводится к отражению, преломлению и дифракции нейтронной волны. Это чисто оптические явления, в которых свойства нейтронов определяются ядерным оптическим потенциалом [7; 8; 9]:

V ( r ) = X, (2 n h¹ / m ) b 5 ( r - r i ) = (2 п h ² / m ) b p ( r ) . (1)

Здесь h - постоянная Планка; m - масса нейтрона; r – текущая координата; ri – положение ядра с номером i; p(r) - плотность частиц рассеивателя; bi [см] – когерентная амплитуда рассеяния на связанном ядре. Величину “ - bi ” называют длиной рассеяния Ферми. Подавляющее большинство ядер характеризуется положительной длиной рассеяния Ферми, но есть некоторое количество ядер с отрицательной длиной рассеяния. Если bi > 0, то нейтронная волна как бы выталкивается из области действия ядерного потенциала, а при bi < 0 втягивается в неё. Суммирование в (1) проводится по всем ядрам рассеивающей системы. Константа b – усреднённое значение амплитуды рассеяния. Потенциал V (r) определяет показатель преломления среды n2 = 1 - V / E, (2) где E – энергия нейтрона, падающего из вакуума. Источником ОХН является ядерный реактор. Однако доля ОХН в спектре реактора очень мала (~ 10-6). Таким образом, использование ОХН в спектрометре затруднено из-за существенного возрастания времени измерений поля рассеянных нейтронов. Тем не менее, уникальные свойства ОХН привлекают внимание экспериментаторов как у нас в стране, так и за рубежом. В частности, в Физическом институте имени П.Н. Лебедева РАН создан и функционирует на базе ядерного реактора МИФИ времяпролётный спектрометр ОХН [6]. Принципиальная схема этого спектрометра имеет вид (см. рис. 1).

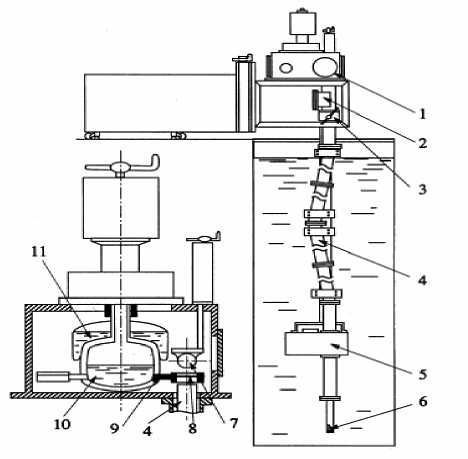
Рис. 1. Схема спектрометра: 1 – камера-криостат;

2 – монитор; 3 – шибер; 4 – нейтроновод; 5 – прерыватель; 6 – конвертор; 7 – счетчик; 8 – образец; 9 – держатель образца; 10 – низкотемпературная ванна; 11 – азотная рубашка

Спектрометр очень холодных нейтронов

Времяпролётный спектрометр, представленный на рис. 1, предназначен для измерений зависимостей полных сечений взаимодействия ОХН с веществом от скорости налетающих из вакуума нейтронов. Исследуемые образцы помещаются в измерительную камеру-криостат. Спектрометрия осуществляется по времени пролёта шестиметровой пролётной базы от механического прерывателя потока нейтронов до детектора. Выделение ОХН из спектра реактора происходит в вакуумируемом нейтроноводе. ОХН, отражаясь от его стенок, выводятся из пучка более быстрых и не отражающихся от стенок нейтронов. В качестве источника нейтронов используется бериллиевый конвертор, смещающий спектр нейтронов в область меньших энергий, расположенный в ячейке активной зоны реактора. В непосредственной близости от измерительной камеры находится счетчик-монитор потока нейтронов. Измерения производятся с образцом и без него для определения падающего No и прошедшего через образец Ntr потоков нейтронов. Такой ме- тод измерения называется методом ослабления. Макроскопическое полное сечение ослабления St определяется отношением прошедшего потока излучения к падающему потоку:

S t = ( 1/ х ) ln ( N o I N_№ ) . (3)

В формуле (3) x – это толщина образца. Скорость нейтрона в вакууме v определяется по времени пролёта из соотношения t = ^ ( v I g ) ² + 2 L I g - ( v I g ) . В качестве детектора нейтронов используется специальный ³ Не – счетчик с давлением гелия 500 тор и эффективностью регистрации ОХН ~100%. Такой детектор практически нечувствителен к тепловым нейтронам.

Поскольку ОХН обладают ярко выраженными оптическими свойствами, то при определении полного сечения необходимо вводить поправки на преломление нейтронной волны на границе вакуум/образец и на многократное отражение от границ образца. Первая поправка сводится к вычислению эффективной скорости нейтрона в образце v' :

• v' =7 v ² - v ² , (4)

где v_r – граничная скорость для вещества, при которой происходит полное отражение нейтронов при любом угле падения на образец. Методика введения второй поправки более сложна и подробно описана в работе [6].

Рассмотрим теперь составляющие полного макроскопического сечения взаимодействия ОХН с веществом S t :

St = Sc + S^ + SH + Ses . (5)

Здесь Sc - сечение захвата нейтрона, Se -сечение неупругого рассеяния нейтронов на колеблющемся в тепловом равновесии ядре исследуемого вещества, SH - сечение упругого некогерентного рассеяния на ядрах вещества, Ses - сечение упругого рассеяния на неоднородностях ядерного оптического потенциала рассеяния. Неупругое рассеяние приводит к нагреванию нейтронов. Поскольку эффективность регистрации тепловых нейтронов детектором много меньше эффективности регистрации ОХН, сечение неупругого рассеяния рассматривают как сечение поглощения, наряду с сечением захвата (1/v) . Сечение упругого некогерентного рассеяния не зависит от скорости нейтрона и определяется исключительно рассеивающими свойствами ядер исследуемого вещества. Известная зависимость перечисленных сечений от скорости нейтрона позволяет исключить из полного сечения вклад чисто ядерных и неупругих процессов взаимодействия и выделить зависимость сечения упругого рассеяния ОХН на элементах наноструктур от скорости нейтронов.

Теоретические основы метода рассеяния ОХН

Фундаментальная величина в нейтронной оптике - это когерентная волна, ^ ( r ). Она обеспечивает полное описание всех когерентных упругих процессов рассеяния и удовлетворяет уравнению Шрёдингера [8]:

• [ ( h ² 12 m ) А + V ( r ) ] ^ ( r ) = E ^ ( r) ,          ⁽⁶⁾

• V ( r ) = (2 п Й ² / m )^ b i < 5 ( r - r i ) > =

i

• = (2 п Й ² / m ) <  b ( r ) >= (2 п Й ² / m ) p bS ( r ),   (7)

• [ 1, при r eQ

где S ( r ) =)            - функция формы, О -

• [ 0, при r ^Q

объём рассеивателя.

В уравнениях (6) и (7) V ( r ) – это оптический потенциал в кинематической теории рассеяния, E – энергия падающего нейтрона, m – масса нейтрона. Потенциал V ( r ) и решение ^ ( r ) - это макроскопические величины, зависящие только от термодинамического состояния системы. В газах, жидкостях и аморфных твердых телах потенциал V ( r ) – константа. В кристаллах – плавно меняющаяся периодическая функция r . Её период равен периоду решётки.

Сечение рассеяния ОХН может быть вычислено в случае, когда поле, на котором происходит рассеяние, может рассматриваться как возмущение, а в качестве возмущения берётся полная потенциальная энергия частицы во внешнем поле: потенциальная энергия нейтрона в среде V ( r ) (1). Такой метод в теории столкновений называют борновским приближением [10]. Это приближение возможно при выполнении условия

I V | <<  h v I a = Й ² k ²I mak = E I ak .         (8)

Здесь a – радиус действия поля V ( r ), V – порядок величины потенциальной энергии нейтрона в основной области ее существования. Из условия (8) следует, что приближение справедливо для достаточно быстрых частиц, ka >>  1. Для ОХН условие (8) нарушается, если a >  R o ^ EI Vk = k I k ².

С увеличением скорости нейтронов значение R_o возрастает, и область применимости приближения Борна уменьшается. Величина полного сечения рассеяния также уменьшается [11]. Условимся различать рассеяние ОХН на отдельной частице [12] и рассеяние на флуктуациях среды (например, флуктуации плотности или магнитной индукции). Во многих реальных слу-

ВЕСТНИК 2016

ВЕСТНИК 2016

чаях невозможно сказать что-либо определенное о форме неоднородностей. Моделировать рассеяние в таких средах удобно, подобрав корреляционную функцию, адекватно отражающую реальный процесс рассеяния. Данные об общих свойствах корреляционной функции можно получить из анализа зависимостей макроскопического сечения от волнового числа k [13–15].

Дифференциальное сечение упругого рассеяния ОХН на неоднородностях образца в бор-новском приближении теории возмущений имеет вид [13–15]:

употребляемых корреляторов – экспоненциальный (пуассоновский) коррелятор, для которого корреляционная функция имеет вид:

K ( R ) = K (0)exp ( - R / l c ) .

Здесь R = |r 1 - r ₂| , l c - корреляционная длина, K (0) = ^ ( 1 - (p )( A p ) ² .

d^eV ) = f    1 Л ^v ( r ^{1 r} ' ) e" r r d r d ^r ' (см 2 ).    (9)

d 2    V 2 n n

Здесь S _es (см -1 ) - макроскопическое сечение упругого рассеяния, V ₂ - объем образца, 5 V ( r ) = V ( r ) -< V >  - флуктуация рассеивающего потенциала, K _{5 V 5V}■ ( r | r ' ) =< 5 U ( r ) 5 U ( r ' ) >  - корреляционная функция флуктуаций 5 V ( r ) и 5 V ( r ' ), q = k - k ' , k и k ' - волновые векторы нейтронов до и после рассеяния соответственно, m – масса нейтрона. В случае изотропной и однородной среды корреляционная функция

зависит только от модуля разности векторов

p =| r - r ' |, а дифференциальное сечение

d S s d 2

оказывается зависящим только от модуля передаваемого нейтрону импульса [13; 14]:

dS     f m

— = 4П---г

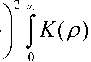
sin qp -----p d p.

qp

S

Интегральное сечение рассеяния

es

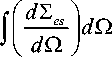
2 k

2n r

d S s d 2

qdq =

2 R,r2 "

. . I '      f ^{K (} p ^{)( 1 -} cos² k p ) ^d p .

2П n J k о

При учёте размеров детектора нейтронов, вместо (11) мы будем иметь:

_y    2 n ² k f d Si ,

5_ =             qdq = es    k2      (d 2)

k sin @ 0

f m 1 2 8 n ² "

= I ^ , ■ I "7 2 " f ^K ( p ) [^{cos(2 k} p ■ ^S 0 ) ^{- cos2k} p ] d p , (12)

V 2 n n J k 0

где 2 @ ₀ - угол, под которым «виден» детектор нейтронов из образца, S ₀ = sin @ ₀ .

Во многих случаях невозможно сказать что-либо определённое о форме неоднородностей. Моделировать в таких средах можно, подобрав соответствующий коррелятор, адекватно отражающий реальные процессы рассеяния в случайно неоднородных средах. Один из наиболее

Величина l c = f K ( p ) d p / K (0) называется длиной корреляции в ⁰ озмущения [15] и определяет эффективный размер неоднородностей; p - объёмная доля рассеивателей, A p = ( N i b i - N j b j ) -перепад длин рассеивающей плотности на границе рассеиватель/матрица. Рассматриваемая

статистическая модель

K ( rjr 2 ) = K (0) N ( rjr 2 )                  (14)

должна быть устойчивой по отношению к изменению вида коэффициента N ( r ₁ | r ₂ ). Можно полагать, что имеется некоторый класс функций, внутри которого изменение вида коэффициента корреляции не изменяет основных результатов. В данном случае такой класс функций образуют функции N ( r ₁ | r ₂ ), имеющие отличную от нуля первую производную при |r 1 - r ₂1 = 0. Другой хорошо известный и широко используемый коррелятор – гауссовский:

K ( R ) = K (0)exp ( - R / l c ) ² .                (15)

Для пуассоновского коррелятора из соотношения (12) получим

S _es = ( 8 п ² / k ² ) K (0) l c X

X

( 1 + 4 k ² l c ² sin ² 9 o )^- 1 - ( 1 + 4 k ² l c ² )" 1 ,

а для гауссовского коррелятора

£ es =(8n 2/ k2 )(n1/2 K (0) lc) X x^exp (-4k2lc2 sin2 6o) - exp (-4k2lc2 )J.

При исследовании случайно-неоднородных конденсированных сред с помощью ОХН основной задачей является нахождение однократно рассеянного поля. Эта задача фактически сводится к вопросу о возбуждении полей заданными случайными источниками, непрерывно распределёнными по объёму V ₂ . Однако в силу конечности радиуса корреляции неоднородностей непрерывное распределение источников равносильно конечному числу дискретных источников [15].

Дифференциальное макроскопическое сечение рассеяния d S _es I d 2 ОХН на N изолированных рассеивателях, заключённых в объёме V ₂ , имеет вид:

(dSes I dQ) = (dS' / dQ)N I VQ = = vp 2 ( pp - Ps )2 p (q) s (q) n । V .

Здесь d S' I d Q - «микроскопическое» дифференциальное сечение рассеяния на отдельно взятом рассеивателе, V_p – объём рассеивателя, q = k - k ' , k и k ' - волновые векторы нейтронов до и после рассеивания соответствен- 22

но, ( P p - P s ) =_ П р Ь р - n_sb_s J = т - контраст рассеиватель-матрица, P ( q ) – форм-фактор рассеивателя, S ( q ) – структурный фактор центров частиц, связанный с корреляционной функцией Ван Хова G ( r ) [7]:

P^{( q} )=^ ^p

j" exp ( i qr ) d r

V p

P (0) = 1, (19)

^{S (} q ) = i n

Z e

l , j

—

= J G(r) e'qr dr, G(r) = 5(r) + Gd (r), функция Gd (r) может быть выражена через парную корреляционную функцию [7], q – передаваемый импульс, 6 - угол рассеяния, q = 2 k sin (612), угловые скобки означают усреднение по ансамблю.

Для наночастиц различной формы (изолированные сферы, цилиндры, в том числе полые, эллипсоиды и так далее) в работах [11; 12; 16; 17] с помощью уравнений (18), (19) из соотношения (11) получены полные сечения рассеяния S _es . При этом учтено, что S ( q ) ^ 1 для больших углов рассеяния. Для вычисления числовых значений S _es использовались алгоритмы, изложенные в работах [18–19]. Время вычисления можно существенно сократить, если воспользоваться методами волновой теории катастроф [20–26].

Главная трудность в применении наночастиц при создании новых материалов – их склонность к агломерации. В частности, макроскопические свойства нанокомпозиционных материалов зависят от равномерности распределения частиц наполнителя в матрице полимера. Кроме того, многие случайные среды являются фрактальными структурами. Частицы-рассеиватели радиуса R (шкала малых расстояний < 10 нм) организуются в кластеры размером £ (^ ~10R), а их объединения образуют гель. На шкале больших размеров – гель-гомогенное пористое стекло. Кластер имеет внутреннюю структуру, описываемую на языке фракталов. В биологических системах это протеиновые агрегаты; в колло- идной химии и химии полимеров – коагуляция, флоккуляция, образование гелей; в металлургии – нуклеация и процессы роста. Оказывается, что кластеры часто имеют значительную степень самоподобия. Для описании геометрического расположения частиц в кластере используется фрактальная размерность D . Теория фракталов позволила ввести новые количественные показа- тели структур в виде фрактальной размерности. Рассматриваются массовые (1 < D < 3) фракталы и поверхностные 2 < DS < 3 фракталы. Для простейшей фрактальной среды со структурами порядка £, созданных из дискретных рассеива телей размером R0 < r < £, R0 << £ , корреляци- онная функция плотности имеет вид [27]:

< P ( r ) P ( 0 ) >= ф ( 1 — Ф )( N 1 b — N 2 b 2 ) 2 ^х х ( D v I4 п ) exp ( - r I § )( R 0 1 r ) 3 - D^V .

Среда предполагается изотропной и однород- ной в среднем, и корреляционная функция тог- да зависит только от модуля разности векторов r = |r1 - r2|; (1 - ф) - часть объема образца, занятая фракталами, DV – размерность объемного фрактала, Nibi – длины ядерных плотностей. В борновском приближении, учитывая (9), (10), дифференциальное сечение упругого рассеяния фракталом принимает форму:

d Q = J < P (0) P (r) >  e i ^{q ( r 1} - r ² ) d r d r =

= ф ( 1 - ф )( N 1 b 1 - N 2 b 2 ) ² VDR 3- D V ^           (22)

dvГ(Dу -1)sin[(Dу -1)arctg (q^)J ^       (4п)2 q (q2 + e )(DV -1)12        , (см2), где Vdv = V3 (R0I ^)3-DV, V3 = ^3, Г(x) - гамма-функция, q = 2ksin (612) - переданный импульс, k - волновое число, 6 - угол рассеяния. Полное макроскопическое сечение упругого рассеяния получено нами из (11):

es

ВЕСТНИК 2016

^ ( 1 - _Ф )( N , b 1 - N 2 b ₂ ) 2 D v 8 n R 0D V - 3 • k²

■Г ( D v - 2 ) ^ D V ^{- 2} .

-

cos [ ( D V - 2 ) arctg ( 2 k ^ ) ]

ВЕСТНИК 2016

Заключение

Значимость наноструктур как фактора, определяющего макроскопические свойства вещества, стимулирует, с одной стороны, совершенствование традиционных методов ее изучения, с другой – поиск и разработку теоретически и экспериментально – новых методов.

Для исследования наноструктур наиболее широко используется электронная микроскопия, рентгеновская дифракция и малоугловое рассеяние рентгеновских лучей, а также нейтронов, однако наряду с неоспоримыми достоинствами они обладают существенными недостатками. Так, например, электронная микроскопия требует сложной предварительной подготовки образца толщиной от 10 ^{- 2} до 10 мкм. С помощью рентгеновских лучей нельзя исследовать магнитные структуры. Метод малоуглового рассеяния нейтронов относится к сложным и дорогостоящим методам.

Развитие нейтронных методов исследования вещества, использующих высокопоточные пучки нейтронов, привело к созданию уникальных установок на импульсных и стационарных реакторах, таких, как трехкристальные спектрометры, спектрометры обратного рассеяния, малоугловые дифрактометры с высоким разрешением по переданному импульсу и др. Создание и функционирование подобных приборов требует больших затрат, высокого уровня математического обеспечения и т.п. В то же время, использование для исследования нейтронов очень низких энергий значительно упрощает экспериментальные установки, хотя и усложняет теоретическое обоснование.