Исследование напряженно-деформированного состояния эндопротезированного тазобедренного сустава

Эндопротезирование тазобедренного сустава в настоящее время является широко распространенным способом лечения заболеваний опорно-двигательного аппарата. Замена больного сустава на искусственный позволяет устранить или значительно уменьшить болевой синдром, обеспечить опороспособность конечности, восстановить движение в суставе. Однако срок службы современных эндопротезов, изготавливаемых из легированных сталей и титана, ограничивается в среднем 10 годами. Проведение повторной операции эндопротезирования зачастую невозможно из-за большого количества противопоказаний и высокого риска развития послеоперационных осложнений. Потребность в эндопротезировании в России составляет до 100-300 тысяч операций в год [9], поэтому продление эксплуатационного ресурса эндопротеза является актуальной медицинской, технической и социальной проблемой.

По данным, представленным в работе [12], в 69,7% случаев несостоятельность эндопротеза вызвана его расшатыванием. Риск расшатывания растет пропорционально давности операции, и в настоящее время данная проблема на имеет какого-либо технического решения. Согласно биомеханической гипотезе основной причиной расшатывания эндопротеза является неадекватность функциональных напряжений, испытываемых костью в системе кость-имплантат при физиологических нагрузках. В наиболее нагруженных местах из-за постоянного микротравмирования костной ткани

происходит ее замещение соединительно-тканной капсулой. В участках кортикальной кости с недостаточной нагрузкой наблюдается патологическое увеличение пористости.

Большое количество исследований направлено на изучение механических аспектов взаимодействия эндопротеза тазобедренного сустава и костной ткани [18, 21, 24, 29, 31, 33, 35–37, 41–43], особое внимание уделено определению влияния конструкции эндопротеза на напряженно-деформированное состояние кости. Экспериментальные исследования выявили особенности влияния конструкции эндопротеза на перераспределение внешней нагрузки в костной ткани. Недостатком экспериментальных методов исследования являются технические ограничения, не позволяющие моделировать сложные условия нагружения системы кость – имплантат, обусловленные физиологической активностью человека. Кроме того, для описания процессов, протекающих в костной ткани, необходима регистрация напряжений внутри кортикального слоя бедренной кости, которая также трудноосуществима при экспериментальном подходе. Поэтому все большую популярность приобретают методы математического моделирования механического поведения системы кость – эндопротез. При этом полученные экспериментальные данные используются для верификации параметров и оценки адекватности математических моделей.

В исследованиях авторов для расчета напряжений, возникающих в костной ткани при функциональных нагрузках, строится пространственная модель тазобедренного сустава с установленной металлической бедренной компонентой эндопротеза. Адекватность предложенной механической модели подтверждается экспериментальными исследованиями. Для определения сил, действующих на тазобедренный сустав при физиологических нагрузках, используется квазистатическая модель ходьбы. Модель ходьбы учитывает пассивное сопротивление связок в суставе, изменение точки приложения опорной реакции, а также ограничения на максимальную изометрическую силу мышцы. Расчет силы реакции в суставе и величины мышечных усилий в различные фазы шага осуществляется с использованием линейных критериев оптимальности. Построенная биомеханическая модель системы кость–эндопротез и вычисленные функциональные нагрузки на сустав позволили рассчитать напряженно-деформированное состояние элементов системы в наиболее нагруженные фазы шага и оценить влияние конструкции имплантата на эксплуатационную долговечность протеза.

Биомеханическая модель системы кость–имплантат

Для исследования влияния конструкции имплантата на эксплуатационную долговечность бедренной компоненты эндопротеза были построены три модели искусственного сустава с различным поперечным сечением ножки (рис. 1): овальным (тип I), круглым (тип II), прямоугольным (тип III). Модель ацетабулярного компонента эндопротеза имеет следующие геометрические параметры: внешний диаметр чашки 50 мм, внешний диаметр полимерного вкладыша 44 мм, диаметр головки 28 мм. Внешний вид конструкции тазового компонента эндопротеза изображен на рис. 2. Для построения персональной геометрии тазобедренного сустава in vivo используются данные томографического исследования [11]. Технология проведения томографического исследования позволяет получить серию изображений поперечного сечения нижней конечности. На томографическом снимке (рис. 3) содержится метрический элемент, с помощью которого определяется начало координат и масштабная координатная сетка. Компьютерная обработка томографических данных позволила построить пространственную модель бедренной и тазовой кости, учитывающую индивидуальные анатомические особенности пациента (рис. 4–5).

а

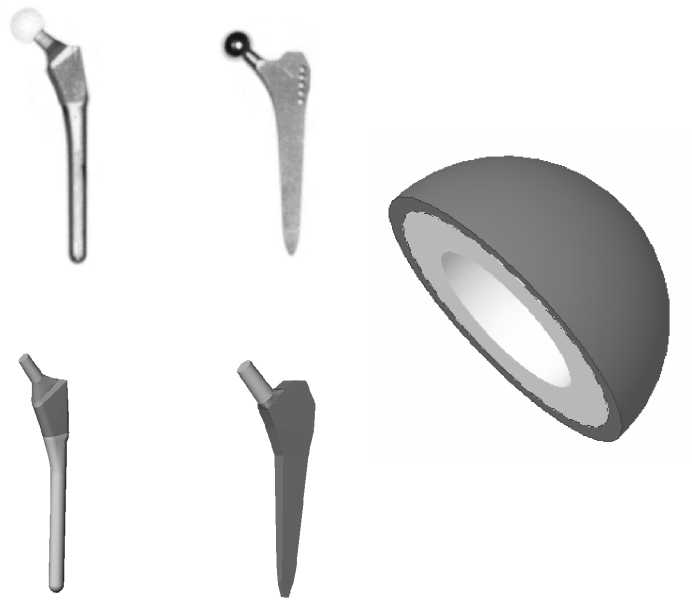
Тип I

Тип II

Тип III

Рис. 1. Внешний вид ( а ) и компьютерные модели ( б ) исследуемых типов конструкций бедренного компонента эндопротеза тазобедренного сустава.

Рис. 2. Модель ацетабулярного компонента эндопротеза.

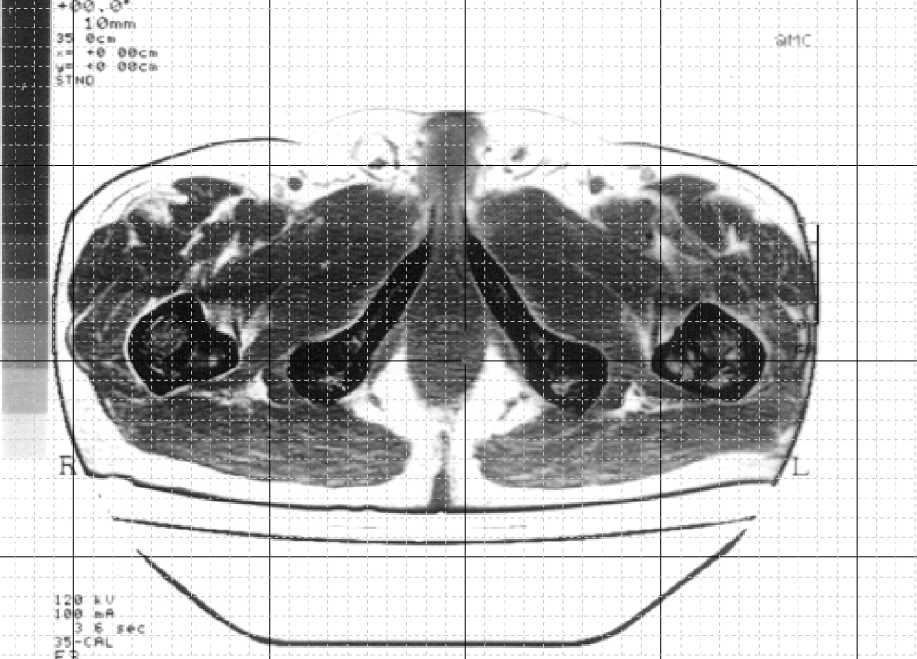
Рис. 3. Томографический снимок с нанесенной координатной сеткой.

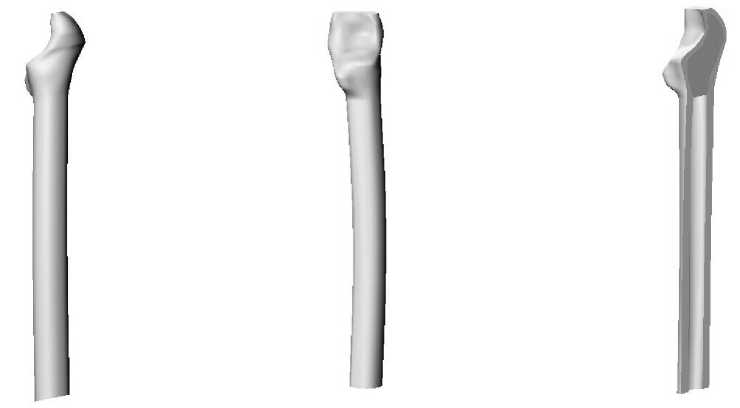
а                           б                            в

Рис. 4. Индивидуальная пространственная модель бедренной кости:

а – фронтальная плоскость; б – сагиттальная плоскость; в – продольный разрез бедра.

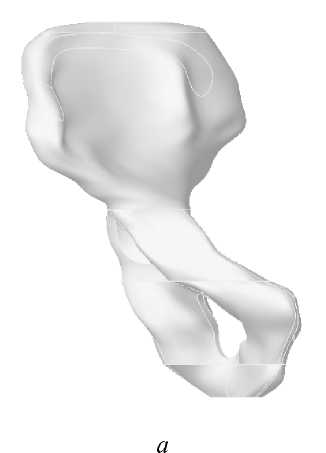
Рис. 5. Индивидуальная пространственная модель тазовой кости: а – фронтальная плоскость; б – саггитальная плоскость.

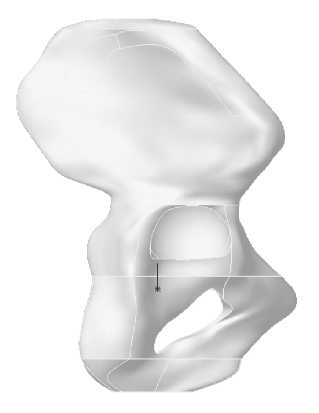
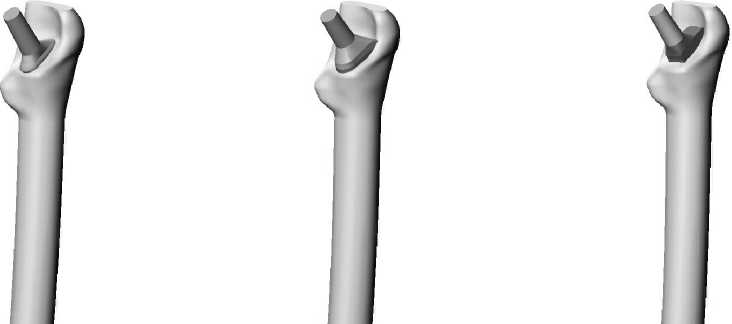
Тип I                               Тип II                                Тип III

Рис. 6. Пространственная модель системы бедро–имплантат.

а

Рис. 7. Модель тазовой кости с эндопротезом: а – фронтальная плоскость, б – сагиттальная плоскость.

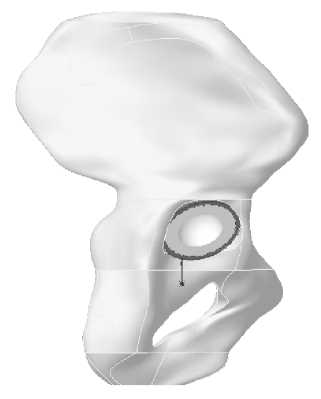
б

Таблица 1

Механические свойства кортикальной костной ткани [15

Независимые величины	Значение, ГПа	Коэффициент поперечной деформации	Значение
E Y	17,10	ν XY	0,25
E X , E Z	8,70	ν YZ	0,50
G XY , G YZ	4,15	ν XZ	0,05
G XZ	4,50

Таблица 2

Механические свойства материалов системы кость–имплантат

Элемент конструкции	Модуль упругости ( E ), ГПа	Коэффициент поперечной деформации (ν)
Тазовая кость	5,0	0,32
Спонгиозная костная ткань	2,50	0,32
Бедренный компонент эндопротеза	210,0	0,30
Металлическая чашка ацетабулярного компонента эндопротеза	210,0	0,28
Полимерный вкладыш ацетабулярного компонента эндопротеза	8,5	0,28

Бедренная кость моделируется как неоднородное анизотропное линейно-упругое тело сложной геометрической формы. Неоднородность механических свойств бедренной кости вызвана наличием костномозгового канала, кортикальной и губчатой костных тканей. Тазовая кость представляется однородным изотропным линейно-упругим телом.

Имплантат размещается в кости с учетом требований пространственной ориентации компонентов эндопротеза. На рис. 6 изображен внешний вид построенных моделей системы бедро–имплантат. Модель тазовой кости с эндопротезом изображена на рис. 7.

Экспериментальному исследованию механических свойств твердых биологических тканей посвящены многочисленные исследования [5, 8, 10, 13, 15, 41]. В табл. 1 приведены данные об анизотропных механических свойствах кортикальной кости, полученные в экспериментальной работе [15]. Необходимые для расчетов значения материальных констант тазовой кости, спонгиозной костной ткани и имплантата приведены в табл. 2.

Механическое поведение системы, занимающей область V в R³ с границей S , в рамках линейной теории упругости описывается следующей системой уравнений:

V-о = 0,                  Vx е V, 1                TT, £ = — (Vu + (Vu)T),           Vx е V , о = E(x): £ ,                 Vx е V , u = 0 ,                         Vx е Su , n - о = 0,                      Vx е S\(( Sp n Sb) u Su u St), n - о -1 = 0,                  Vx е St, (1) (2) (3) (4) (5) (6) где V=VU S, S = Su U St, ст - тензор напряжений; £ - тензор упругих деформаций; E(x) - тензор упругих свойств, Sb - полная поверхность кости, Sp - поверхность имплантата, Sb n Sp - поверхность контакта кости с имплантатом, St - поверхности нагружения, Su - поверхность с ограничениями, заданными в перемещениях.

Исследуемая область является сложной пространственно неоднородной конструкцией, поэтому для расчета напряженно-деформированного состояния системы кость-имплантат используется метод конечных элементов. Исследуемая область аппроксимируется тетраэдрами с линейной аппроксимацией перемещений (рис. 8-9).

Для проверки адекватности принятой модели механического поведения бедренной кости с установленным эндопротезом в лаборатории физико-механических свойств материалов Института механики сплошных сред УРО РАН при участии сотрудников кафедры травматологии, ортопедии и военно-полевой хирургии Пермской государственной медицинской академии было проведено экспериментальное исследование полей продольных деформаций наружного слоя бедренной кости при воздействии на неё вертикальной нагрузки.

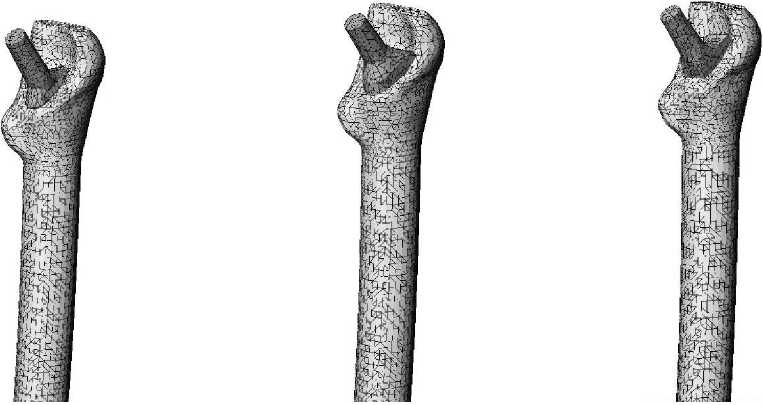
Тип I                                  Тип II                               Тип III

Рис. 8. Конечно-элементная аппроксимация системы бедро-эндопротез.

Экспериментальное исследование продольных деформаций кортикального слоя бедренной кости

На наружной поверхности бедренной кости была нанесена разметка, разделяющая кость на 10 одинаковых участков (рис. 10).

Бедренная кость при помощи специально изготовленных подкладок была установлена в физиологическом положении на испытательном приборе 1925ПА-10М (рис. 11, а ) и нагружена до 3000 Н со скоростью 5 мм/мин.

Продольные поверхностные перемещения регистрировались тензодатчиком наружного крепления с базой 25 мм. Измерения проводились с передней, задней, наружной и внутренней сторон каждого участка.

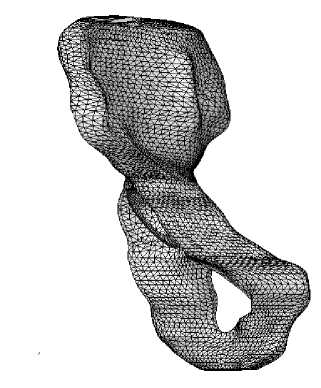
а

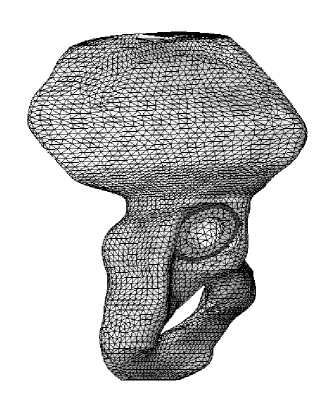
б

Рис. 9. Конечно-элементная аппроксимация системы таз – эндопротез: а – фронтальная плоскость, б – сагиттальная плоскость.

задняя сторона внутренняя сторона

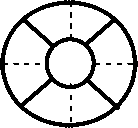
передняя сторона

А – А наружная сторона

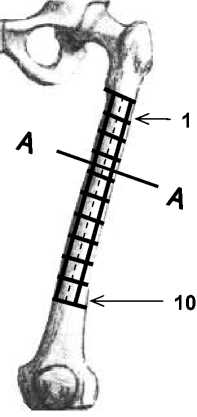
Рис. 10. Участки измерений продольных перемещений.

а

б

Рис. 11. Расположение «здоровой» бедренной кости ( а ) и эндопротезированного бедра ( б ) на испытательном приборе 1925ПА-10М.

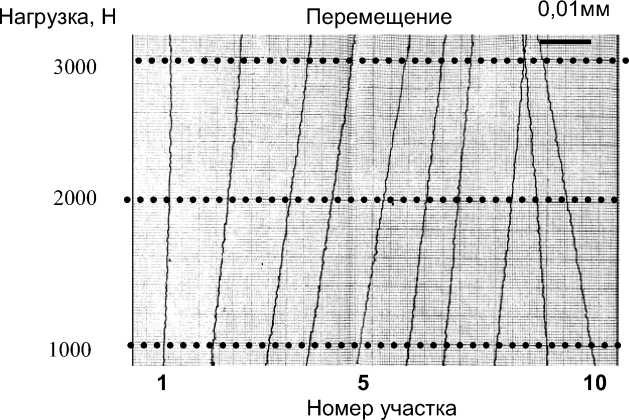
Рис. 12. Графики продольных перемещений, зарегистрированных в 1–10 участках переднего края «здоровой» бедренной кости.

В результате проведенного эксперимента были получены данные о перемещениях в 40 участках бедренной кости. Далее в бедренную кость был установлен эндопротез и проведена повторная серия испытаний (рис. 11, б ).

По измеренным продольным перемещениям (рис. 12–13) были рассчитаны продольные поверхностные деформации «здоровой» и протезированной бедренной кости. Анализ результатов экспериментального исследования показал линейно-упругое поведение системы бедро–имплантат при внешних нагрузках до 3000 Н.

Для проверки адекватности принятой модели механического поведения конструкции бедро–эндопротез была построена пространственно-неоднородная анизотропная линейноупругая модель системы кость–имплантат. За прототип кости была взята бедренная кость трупа 50-летнего мужчины, в которую имплантировался эндопротез модели "Феникс" (рис. 14).

Рис. 13. Графики продольных перемещений, зарегистрированных в 1–10 участках переднего края протезированной бедренной кости.

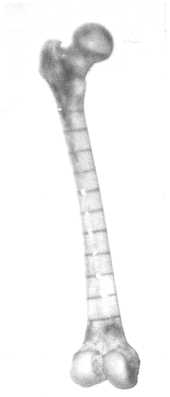
Рис. 14. Бедренная кость и эндопротез модели "Феникс".

При построении конечно-элементной модели бедренной кости с установленным эндопротезом используется ортогональная декартова система координат. Ось Y направляется вдоль продольной оси бедра, ось Z перпендикулярна фронтальной плоскости и образует с осями X , Y правостороннюю систему координат. Исследуемая область (рис. 15) аппроксимируется тетрагональными элементами с линейным распределением перемещений. При расчетах используются механические свойства эндопротеза и костной ткани, приведенные в табл. 1–2.

С помощью построенной пространственной конечно-элементной модели системы бедро–эндопротез были рассчитаны поля продольных деформаций бедренной кости при следующих граничных условиях: нижний край кости консольно закреплен; головка протеза нагружена вертикальной нагрузкой 3000 Н (рис. 16).

Величины поверхностных продольных деформаций на внутреннем и наружном крае бедренной кости, зарегистрированные в эксперименте и рассчитанные при помощи численной модели, представлены на рис. 17.

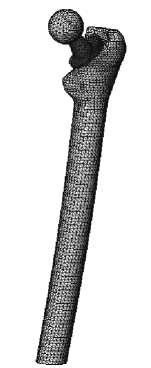
Рис. 15. Пространственная конечно-элементная модель системы бедро–эндопротез «Феникс».

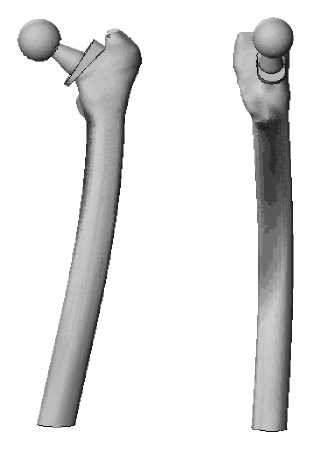
Рис. 16. Граничные условия ( а ) и результаты расчёта продольных деформаций ( б – г ).

г

0,002

0,001

0,0

-0,001

-0,002

Как видно из рис. 17, результаты проведенного экспериментального исследования хорошо согласуются с имеющимися литературными данными. Наблюдаемые различия в величине продольных деформаций у «здорового» бедра вызваны тем, что при проведении испытаний [18] нижняя часть бедренной кости закреплялась консольно, а в исследовании авторов бедренная кость фиксировалась на испытательной машине при помощи специально подготовленной подкладки. Некоторые количественные отличия экспериментальных данных от результатов численного решения обусловлены некоторым несоответствием данных о механических свойствах исследованной бедренной кости и использованием при расчетах значений из литературных источников.

Проведенное экспериментальное исследование показало, что система уравнений (1–6) адекватно описывает механическое поведение системы бедро–имплантат. Использование метода конечных элементов для расчёта напряженно-деформированного состояния данной системы позволяет рассчитать поля деформаций, качественно и количественно подтвержденные в эксперименте.

3000N

ε, %

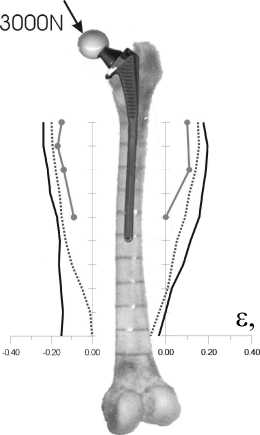
Рис. 17. Продольные деформации на наружном и внутреннем крае «здоровой» и «протезированной» бедренной кости полученные в эксперименте в сравнении с численными расчетами и данными других авторов: по данным [18]; эксперимент;

численное решение.

Для расчета эксплуатационной долговечности конструкции кость–эндопротез необходимо знать все внешние силы, действующие в области тазобедренного сустава при функциональных нагрузках. Большой интерес представляют нагрузки на бедро при ходьбе, являющейся основным двигательным актом человека. Экспериментальные методы измерения мышечной активности во время ходьбы (при помощи регистрации электрической активности мышц) позволяют получить лишь качественные характеристики мышечной активности. Для количественного анализа усилий необходимо применение методов биомеханического моделирования. Исследованию нагрузок на бедро при ходьбе посвящено большое количество работ [7, 17, 20, 22, 23, 25 - 27, 32, 38], которые отличаются постановкой задачи, используемыми критериями оптимальности, числом мышц и сегментов конечности, учитываемых при расчетах.

Построению более точных моделей способствует интенсивное развитие методов регистрации различных параметров ходьбы. Подробные исследования биомеханической структуры нормальной ходьбы приведены в работах [4, 16]. Некоторыми авторами дополнительно были исследованы момент пассивного сопротивления связок тазобедренного сустава [18, 30], движение таза и бедра во фронтальной плоскости [2, 14, 34] и изменение координат точки приложения опорной реакции к стопе [6, 40]. В работах [22, 30, 39] приводятся анатомические данные мышечной системы тазобедренного сустава, необходимые для построения модели нижней конечности.

Биомеханическая модель ходьбы

В исследованиях авторов для расчета нагрузок на тазобедренный сустав и вычисления усилий мышц при ходьбе была построена биомеханическая модель нижней конечности, состоящей из трех сегментов: бедро, голень и стопа. Взаимное расположение сегментов при ходьбе определяется межзвенными углами. Масса, длина, положение центра масс каждого сегмента были вычислены по относительным (к росту и весу тела человека) значениям, приведенным в работах [3, 16]. Расчетные антропометрические данные, использованные в модели, приведены в табл. 3.

Таблица 3

Антропометрические параметры модели

Пол	мужской
Рост, см	175
Вес, кг	68
Сегмент	бедро	голень	стопа
Относительная масса, % (к весу)	11,58	4,75	1,65
Расстояние до центра масс от проксимального сустава, % (к росту)	10,32	10,25	4,32
Относительная длина, % (к росту)	23,80	24,10	13,80

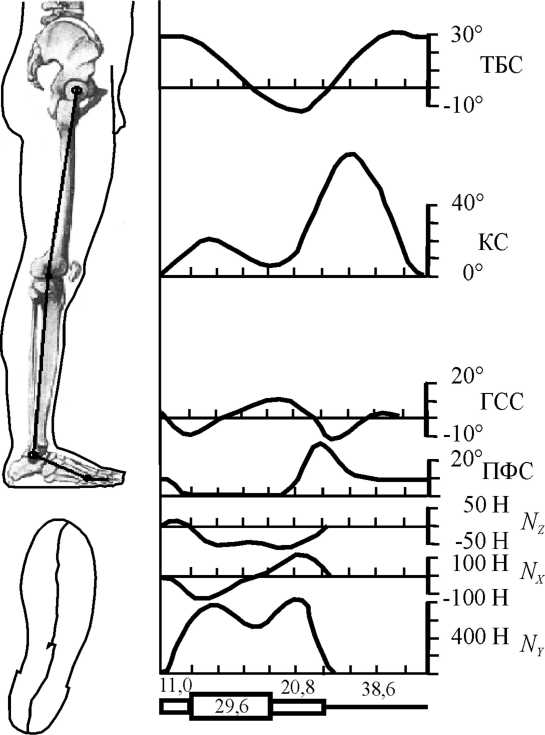
Рис 18. Изменение межзвенных углов в тазобедренном (ТБС), коленном (КС), голеностопном (ГСС) и плюснефаланговом (ПФС) суставах, опорные реакции N_x, N_y, N_z и точка приложения опорной реакции к стопе. Под нижним графиком приведена подограмма и значения продолжительности отдельных фаз шага в процентах от времени двойного шага.

Ходьба моделировалась как квазистатический процесс. Весь цикл двойного шага был разбит на 20 равных участков времени. Данные по опорным реакциям и межзвенным углам при нормальной ходьбе были взяты из работы [4] (рис. 18). Изменение координат точки приложения опорной реакции на стопе в опорную фазу шага было взято из статьи [6].

В модели учитывается действие 27 мышц бедра и таза. Мышца моделируется внешней силой, направленной по прямой, соединяющей точки прикрепления мышцы на бедре и тазе. Координаты прикрепления мышц к бедру и тазу взяты из работы [30]. Момент сопротивления связок тазобедренного сустава в сагиттальной плоскости вычислялся по соотношению, приведенному в работе [28].

M _св (a) = 2,6 e -^^1^⁴⁴⁾ - 8,7 e -w⁰, ⁹⁵- ) ,

где α – межзвенный угол в тазобедренном суставе.

При расчетах используются две системы координат (рис. 19): неподвижная (лабораторная) OXYZ и две подвижных O'X'Y'Z' и OX''Y''Z'', связанные с тазом и бедром соответственно. Начало координат (точка О ) расположена в центре головки бедренной кости. Тазобедренный сустав моделируется сферическим шарниром. Действие таза на бедро заменяется силой реакции в суставе.

В каждую фазу шага по известным межзвенным углам в сагиттальной плоскости и отклонениям таза и бедра от вертикали во фронтальной плоскости (по данным [4, 14]) определялась текущая конфигурация нижней конечности. Для неё вычислялись координаты точек прикрепления мышц, и на каждой фазе шага решалась система уравнений равновесия вида nm

£ F + £ P , + R + N = 0;

i = 1          к = 1

nm

£ M o ( F ) + £ M o ( P k ) + M ig + M o ( N ) = 0; >

= 1                  к = 1

F i ^ 0;

F ^ F max ;

где n - число мышц; m - число сегментов; R - реакция связи в суставе; N - реакция опоры; F i - сила i- й мышцы; P _к - вес к- го сегмента тела ; М _св - момент сопротивления связок; F_{i max} – максимальная изометрическая сила i- й мышцы.

Для расчета максимальной изометрической мышечной силы используется приведенное в работах [7, 24, 26] соотношение

Fmax  Kпр Sфиз cos а, где Кпр - удельная мышечная сила (~ 40 Н/см2); а - текущий угол перистости мышцы. Учитывая, что для веретенообразных мышц Sфиз= Sан, а cos а =1, получим

F max = K пр S ан .

С целью определения S ан , были исследованы 24 мышцы бедра и таза правой нижней конечности. Измерения проводились на трех мужских трупах схожего телосложения и одном живом человеке (по компьютерной томограмме нижней конечности). Измеряемыми величинами являлись: площадь анатомического поперечного сечения ( S ан ), масса, длина брюшка и сухожилия каждой мышцы. По результатам измерений были вычислены некоторые относительные параметры мышц нижней конечности. Использование томографических снимков позволило сравнить результаты измерений на трупах с данными in vivo . Основные антропометрические данные объектов исследования приведены в табл. 4.

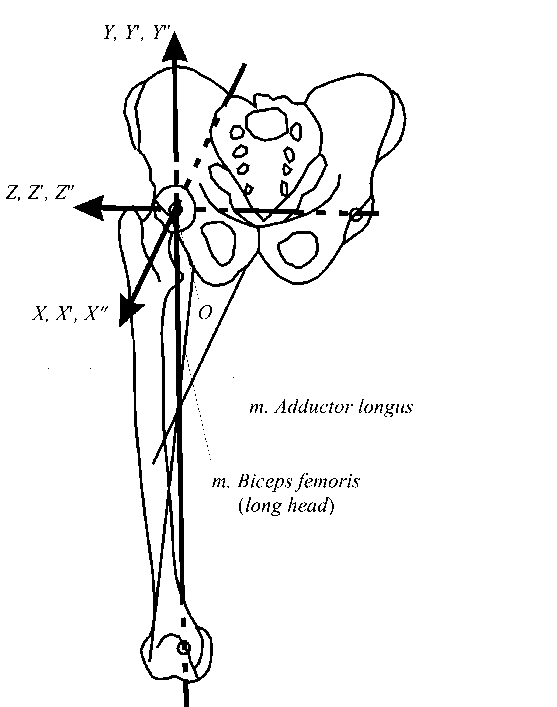
Рис. 19. Системы координат и линии действия некоторых мышц.

Таблица 4

Антропометрические данные объектов исследования

Данные	Объект
	1*	2*	3*	4*
Рост (см)	170	165	168	184
Вес (кг)	70**	65**	77	84**
Возраст (лет)	от 50 до 60	от 50 до 60	74	от 35 до 40

* 1 – первый труп; 2 – второй труп; 3 – живой человек; 4 – третий труп.

** Масса тела (кг) определялась как ≈ рост – 100 см.

На трупах измерения проводились в срок не более трех дней после смерти. Каждая вычлененная мышца взвешивалась, измерялась длина всей мышцы и отдельно длина брюшка, длина проксимального и дистального сухожилий. В общем случае измерение площади поперечного сечения проводилось на пяти срезах: по центру дистального и проксимального сухожилия, а также на срезах брюшка в дистальном центральном и проксимальном участках. Срез окрашивался и делался отпечаток S ан на бумаге. Для уменьшения погрешности измерений делалось по два отпечатка с каждой стороны среза. Пример результатов измерений для m. Rectus femoris приведен на рис. 20.

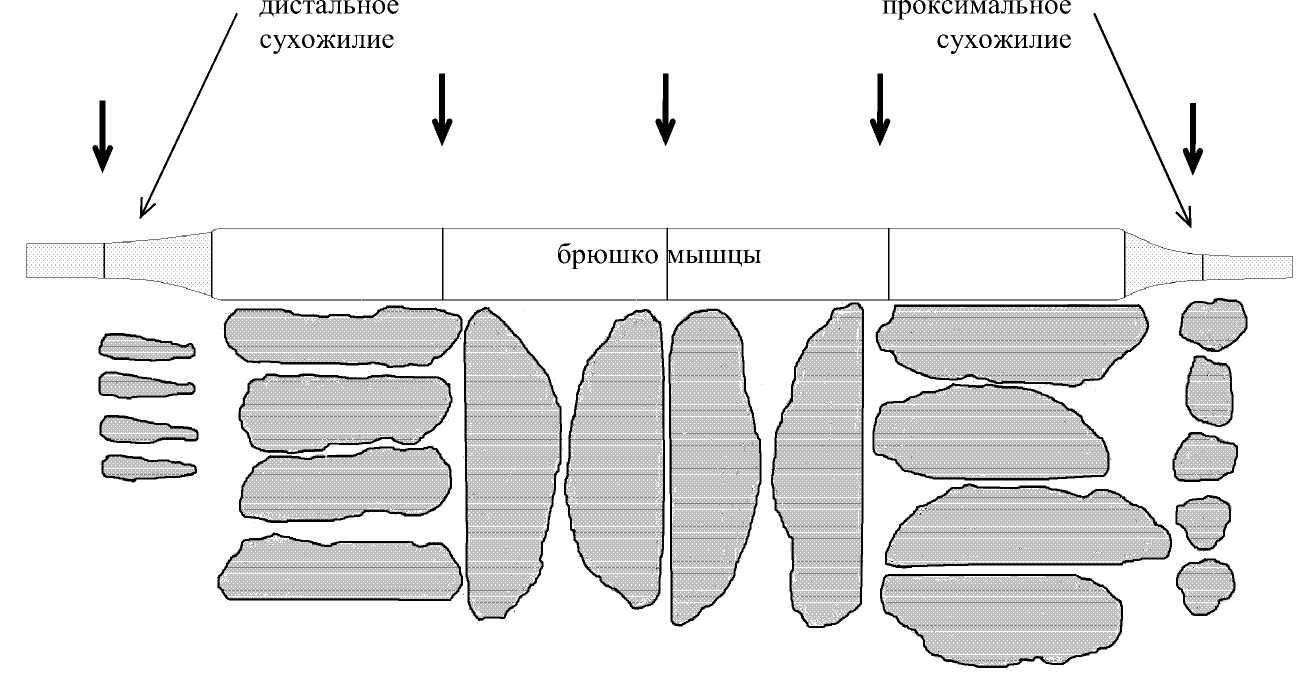
Рис. 20. Отпечатки поперечных срезов брюшка и сухожилия m.Rectus femoris . (стрелками указаны места поперечных срезов).

m. Rectus femoris m .Biceps femoris (long head)

m. Semitendinosus

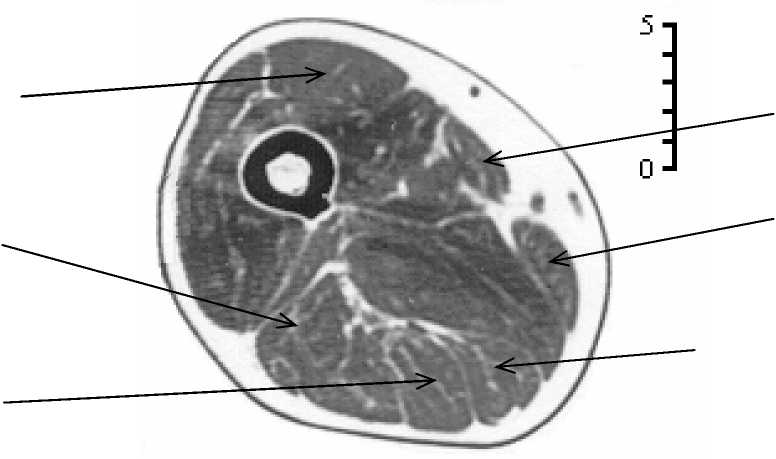
m. Sartorius m. Gracilis

Рис. 21 Томографический снимок диафиза бедра (стрелками показаны некоторые мышцы бедра; масштабная шкала 5 см).

По четырем отпечаткам для каждого среза вычислялось среднее значение S ан . Среднеквадратичное отклонение измерений не превышало 10%. Из полученных значений S ан для дистального, центрального и проксимального срезов брюшка мышцы при вычислениях использовалось максимальное значение.

Для некоторых мышц результаты исследований сравнивались с площадью поперечного сечения измеренной на томографическом снимке ( S том ) бедра живого человека (рис. 21).

Так как плоскость снимка не совпадает с плоскостью поперечного сечения мышцы, то при вычислении S ан по известным S том необходимо учитывать направление мышцы в пространстве. Угол наклона мышечных волокон к плоскости снимка был рассчитан по данным работы [30], в которой приведены точки прикрепления мышц на тазовой кости и на бедре, а мышца рассматривается как прямая линия. Для m. Iliopsoas и m. Rectus femoris приведены значения S том потому, что у m. Iliopsoas направление мышечных волокон изменяется и модель прямых линий не подходит, а у m. Rectus femoris невозможно измерить угол перистости.

Таблица 5

Значения измеренных параметров мышц

Название мышцы	S ан max (см2)				m (г)
	1*	2*	3*	4*	1*	2*	4*
Psoas major	11,29	4,61	15,55	16,71	185	-	265
Iliacus	12,43	11,50	11,31	26,29	175	140	243
Gemellus superior	0,96	-	-	2,15	7	-	10
Gemellus inferior	2,23	-	-	3,93	10	-	10
Obturator externus	7,84	5,99	-	11,80	40	40	85
Obturator internus	10,75	-	-	10,54	59	-	60
Piriformis	4,99	2,22	4,01	6,37	11	20	40
Quadratus femoris	-	8,09	-	5,84		70	37
Pectineus	6,81	3,60	6,54	6,67	58	75	67
Adductor minimus	3,80	-	-	6,98	30	-	68
Adductor brevis	6,46	9,61	9,45	9,79	70	110	128
Adductor longus	12,29	9,40	11,23	13,39	176	180	208
Adductor magnus	26,09	11,26	32,61	26,03	490	260	595
Adductor magnus (ant)	10,40	-	-	4,15	180	-	70
Adductor magnus (med)	6,14	11,26	-	7,25	130	260	170
Adductor magnus (post)	9,55	-	-	14,63	180	-	355
Gluteus minimus	18,43	14,51	9,58	20,38	98	120	141
Gluteus minimus (ant)	5,85	5,77	-	6,05	28	45	37
Gluteus minimus (med)	8,21	5,35	-	6,04	50	45	42
Gluteus minimus (post)	4,37	3,39	-	8,29	20	30	62
Gluteus medius	30,31	21,01	29,44	41,76	265	160	370
Gluteus medius (ant)	5,61	6,93	-	16,35	30	50	115
Gluteus medius (med)	10,81	7,74	-	7,23	78	50	65
Gluteus medius (post)	13,89	6,34	-	18,18	157	60	190
Gluteus maximus	43,64	30,36	34,83	65,89	760	700	1065
Gluteus maximus (inf)	19,85	8,67	-	20,50	420	380	470
Gluteus maximus (sup)	23,79	21,49	-	45,39	340	320	595
Tensor fascia latae	8,74	4,07	9,04	9,22	110	50	110
Semimembranosus	11,58	7,68	6,43	14,61	228	190	275
Semitendinosus	8,88	4,62	8,55	8,83	202	105	190
Gracilis	3,21	3,86	5,57	5,11	100	85	110
Sartorius	3,13	2,68	3,36	4,43	141	125	200
Rectus femoris	12,69	6,77	10,73	15,57	258	165	330
Biceps femoris (long)	10,50	7,86	14,89	13,19	166	-	230
Biceps femoris (brev)	8,87	4,82	4,68	8,43	128	95	140

1 – первый труп; 2 – второй труп; 3 – живой человек; 4 – третий труп.

Результаты исследований приведены в табл. 5–6. В данных таблицах используются следующие обозначения: S _а ^m _н ^ax – максимальное значение анатомического поперечника мышцы; F max – максимальная изометрическая сила мышцы, m – масса мышцы.

Полученные в данном исследовании результаты измерения площади анатомического поперечного сечения ( S ан ) согласуются со значениями площади физиологического поперечного сечения ( S физ ) для женского трупа, приведенными в работе [22]. Использование авторами при исследованиях объектов с похожими антропометрическими данными позволило избежать такого, как в работе [22], разброса значений. Приведенные в табл. 5–6 данные можно использовать для пациентов схожего с исследованными объектами возраста и телосложения. Использование томографических данных живого пациента позволяет определить индивидуальные значения S ан и F max .

Таблица 6

Значения рассчитанных параметров мышц

Название мышцы	F max (Н)
	1*	2*	3*	4*
Psoas major	451,6	184,4	622,0	668,4
Iliacus	497,2	460,0	452,4	1051,6
Gemellus superior	38,4	-	-	86,0
Gemellus inferior	89,1	-	-	157,2
Obturator externus	313,8	239,6	-	472,0
Obturator internus	430,0	-	-	421,6
Piriformis	199,5	88,8	160,4	254,8
Quadratus femoris	-	323,6	-	233,6
Pectineus	272,5	144,0	261,5	266,8
Adductor minimus	152,0	-	-	279,2
Adductor brevis	258,4	384,4	378,1	391,6
Adductor longus	491,8	376,0	449,1	535,6
Adductor magnus	1043,6	450,4	1304,2	1041,2
Adductor magnus (ant)	415,9	-	-	166,0
Adductor magnus (med)	245,8	450,4	-	290,0
Adductor magnus (post)	382,0	-	-	585,2
Gluteus minimus	737,2	580,4	383,2	815,2
Gluteus minimus (ant)	234,1	230,8	-	242,0
Gluteus minimus (med)	328,4	214,0	-	241,6
Gluteus minimus (post)	174,9	135,6	-	331,6
Gluteus medius	1212,4	840,4	1177,4	1670,4
Gluteus medius (ant)	224,5	277,2	-	654,0
Gluteus medius (med)	432,5	309,6	-	289,2
Gluteus medius (post)	555,5	253,6	-	727,2
Gluteus maximus	1745,6	1214,4	1393,1	2635,6
Gluteus maximus (inf)	794,1	346,8	-	820,0
Gluteus maximus (sup)	951,5	859,6	-	1815,6
Tensor fascia latae	349,7	162,8	361,7	368,8
Semimembranosus	463,3	307,2	257,3	584,4
Semitendinosus	355,3	184,8	342,2	353,2
Gracilis	128,4	154,4	222,6	204,4
Sartorius	125,2	107,2	134,5	177,2
Rectus femoris	712,0	270,8	429,4	622,8
Biceps femoris (long)	420,0	314,4	595,5	527,6
Biceps femoris (brev)	354,6	192,8	187,2	337,2

* 1 – первый труп; 2 – второй труп; 3 – томографические данные; 4 – третий труп.

Система уравнений (8) является статически неопределимой, так как число неизвестных больше числа уравнений. Решить данную задачу можно, используя некоторый критерий поиска оптимального решения. Рассмотрим несколько линейных критериев оптимальности.

J 1 = E F ^ min, J 2 = E F -Mmax ^ min, J 3 = Ей H min,         (11)

i = 1                            i = 1                                         i = 1

где A_i – работа, совершаемая i- й мышцей при ходьбе.

Работа вычисляется как произведение силы мышцы на изменение длины мышцы в заданную фазу шага.

На рис. 22 изображен график изменения компонент момента мышечных сил за время двойного шага. График момента мышечных сил относительно сагиттальной оси ( M z ) имеет два выраженных максимума, совпадающих по фазе с передним и задним толчками.

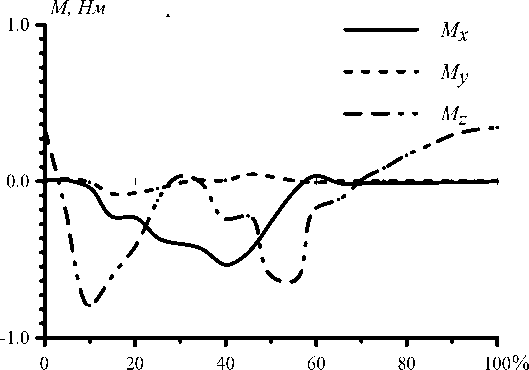
Рис. 22. Момент мышечных сил относительно осей лабораторной системы координат за время двойного шага.

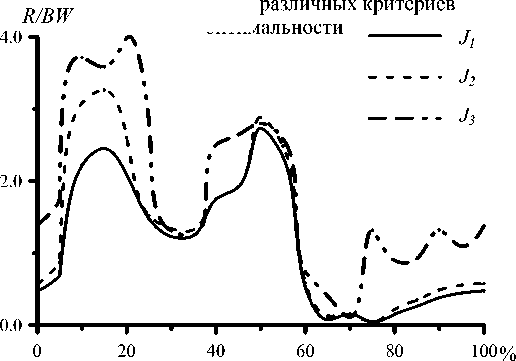
Рис. 23. Значения относительной (к весу тела BW ) реакции в тазобедренном суставе, вычисленные при различных критериях оптимальности.

Таблица 7

Работа мышц, вычисленная по различным критериях оптимальности

Критерий	Работа мышц, Дж
	положительная	отрицательная	алгебраическая сумма	сумма модулей
J 1	14,456	–9,746	4,710	24,202
J 2	15,151	–9,880	5,271	25,031
J 3	13,310	–8,895	4,414	22,205

На рис. 23 изображен график изменения реакции в тазобедренном суставе, рассчитанный с использованием различных критериев оптимальности. График реакции в суставе имеет два максимума, соответствующих переднему и заднему толчкам. Величина первого максимума зависит от выбранного критерия оптимальности.

В табл. 7 приведены расчетные значения работы мышц нижней конечности для различных критериев оптимальности. Абсолютное значение работы для различных критериев изменяется незначительно (в пределах 10%), а величина реакции в суставе в момент переднего толчка различается в 2 раза. Таким образом, при незначительном выигрыше в затраченной работе имеем значительное увеличение нагрузки на сустав.

При расчетах учитывалось действие 27 мышц бедра и таза. Для различных критериев оптимальности число участвующих в движении мышц изменялось. На рис. 24 – 25 показаны мышцы, активные во время переднего и заднего толчков. Как видно из рис. 24 – 25, активность m.Gluteus medius , обеспечивающей поддержание вертикальной позы во фронтальной плоскости, не зависит от выбора критерия поиска решения, а передвижение тела вперед обеспечивается по-разному. При использовании первого критерия движение осуществляется задней группой мышц ( m. Biceps femoris, m. Semitendinousus ). При втором критерии движение осуществляется крупными мышцами ( m. Gluteus maximus ), что приводит к увеличению нагрузки на сустав. При использовании третьего критерия движение нижней конечности осуществляется мышцами внутренней группы, что также приводит к значительному увеличению нагрузки на сустав.

Значение F max пропорционально площади поперечного сечения мышцы с коэффициентом пропорциональности К пр = 40 Н/см². Так как К пр может зависеть от физической формы человека, то была проверена зависимость решения от ограничений на силу мышц. Величина К пр изменялась от 20 до 60 Н/см². Сравнение показало, что при первом критерии оптимальности решение слабо зависит от К пр и уменьшение значения приводит к тому, что в работу задней группы мышц включается и мышца m. Semimembranosus . Для второго критерия при уменьшении К пр к работе m. Gluteus maximus добавляется работа мышц задней группы, а нагрузка на сустав почти не меняется. При использовании третьего критерия уменьшение К пр ведет к уменьшению нагрузки на сустав (на 25%) во время переднего толчка, незначительному увеличению работы и дополнительной активности задней группы мышц.

Использование К пр = 60 Н/см² приводит к увеличению нагрузки на сустав (на 25%) во время переднего толчка при незначительном увеличении общей работы. Таким образом, при решении задачи с третьим критерием оптимальности наблюдается значительная зависимость решения от индивидуальных особенностей человека. Так как применение при расчетах второго критерия оптимальности приводит к возрастанию нагрузки на сустав и увеличению работы мышц, то предполагается, что первый критерий оптимальности позволяет найти решение, наиболее точно описывающее биомеханику ходьбы.

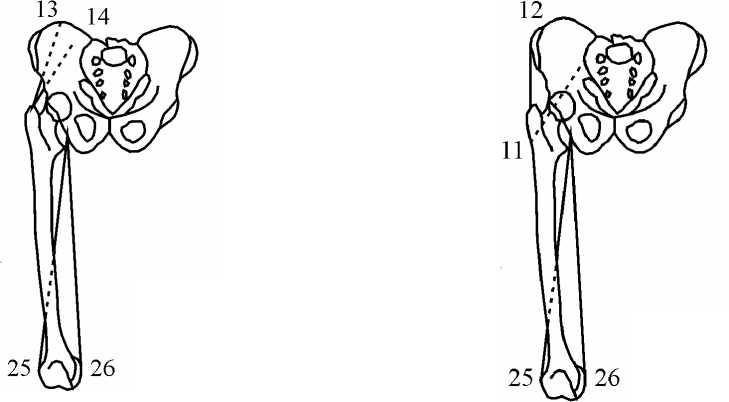
Рис. 24. Активные мышцы при переднем (слева) и заднем (справа) толчках; (по результатам расчетов с использованием первого критерия оптимальности).

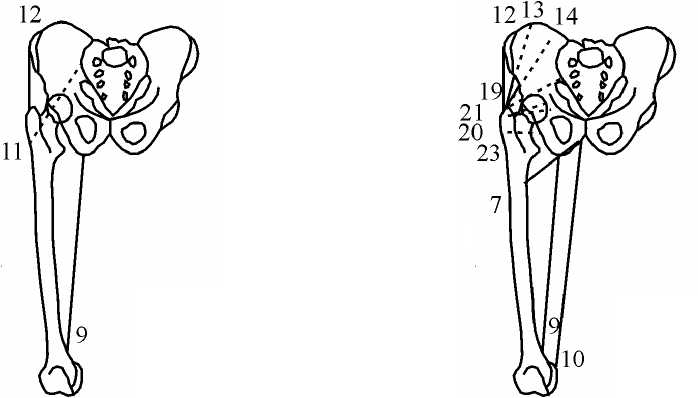
Рис. 25. Активные мышцы при переднем (слева) и заднем (справа) толчках;

(по результатам расчетов с использованием второго (слева) и третьего (справа) критериев оптимальности).

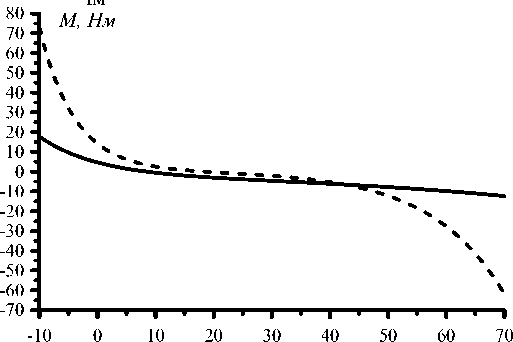
угол, град

Рис. 26. Зависимость момента пассивного сопротивления в суставе М СВ от величины межзвенного угла в тазобедренном суставе по данным разных авторов: [28] (сплошная линия) и [44] (штриховая линия).

20       40

60       80       100 %

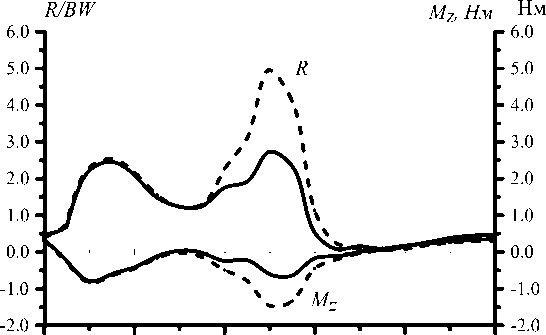
Рис. 27. Зависимости относительной (к весу тела) реакции в тазобедренном суставе и момента мышечных сил относительно сагиттальной оси, рассчитанные при использовании данных разных авторов: [28] (сплошная линия) и [44] (штриховая линия).

Для оценки влияния на решение данных различных авторов были проведены дополнительные расчёты. Соотношения для расчёта момента пассивного сопротивления в суставе ( М св ) приводятся в работах [28, 44]. На рис. 26–27 показаны графики зависимости М cв от угла сгибания бедра и зависимость решения от используемого при расчетах соотношения. Как видно из графиков, использование при расчетах соотношения из работы [44] приводит к значительному увеличению нагрузки на сустав во время второго толчка. Результаты сравнения данных по координатам точки приложения реакции опоры к стопе в опорную фазу шага, полученные в работах [6] и [40], приведены на рис. 28–29.

На графиках видно, что от выбора данных зависит, какой максимум больше: первый или второй, картина усилий в мышцах остается идентичной, только увеличивается активность задней группы мышц в начальный период опорной фазы, совпадающей с передним толчком. Однако работа мышц при ходьбе существенно возрастает (табл. 8).

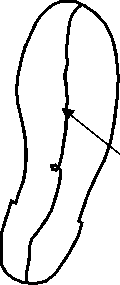
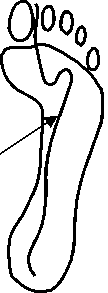
Таблица 8

Работа мышц, вычисленная по данным [6] и [40]

Авторы	Работа, Дж
	положительная	отрицательная	алгебраическая сумма	сумма модулей
С.И. Душин, Е.Н. Свечкопал [6]	1,446	–0,975	0,471	2,420
Y. Suto, B.E. Kawamura [40]	2,631	–0,522	2,109	3,154

Рис. 28. Изменение координат точки приложения реакции опоры к стопе в опорную фазу шага, по данным [6] (слева) и [40] (справа).

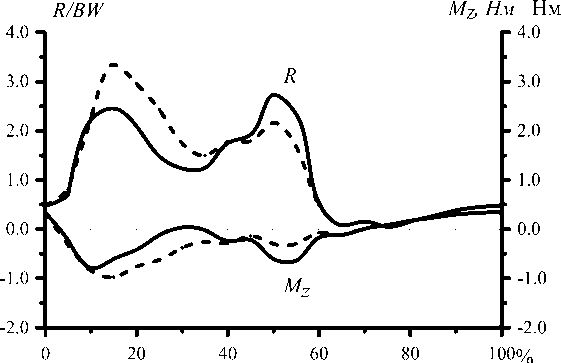
Рис. 29. Зависимость относительной (к весу тела) реакции в тазобедренном суставе и момента мышечных сил относительно сагиттальной оси, рассчитанные при использовании данных разных авторов: [6] (сплошная линия) и [40] (штриховая линия).

Таким образом, с помощью построенной биомеханической модели нижней конечности человека рассчитаны нагрузки, действующие на тазобедренный сустав при нормальной ходьбе. В модели учитывается активность 27 мышц бедра и таза. Полученные результаты хорошо согласуются с решениями других авторов. Вычисленные усилия в мышцах и сила реакции в суставе используются при расчете напряженно-деформированного состояния нижней конечности.

Расчет напряженно-деформированного состояния костной ткани

Напряженно-деформированное состояние системы кость–эндопротез исследуется в рамках линейной теории упругости при ходьбе. При расчетах картины распределения напряжений в кости используется ортогональная декартова система координат. Начало системы координат располагается в центре бедренной головки. Для задания статических и кинематических граничных условий используются данные о величине мышечных сил и реакции в суставе в наиболее нагруженные фазы шага (фаза переднего и фаза заднего толчков). На границе контакта эндопротеза с костной тканью предполагается наличие биофиксации. Технологические напряжения, возникающие при установке имплантата в кость, считаются незначительными.

Согласно литературным данным на первом этапе развития асептической нестабильности эндопротеза в результате микротравмирования кости происходит замещение костной ткани соединительно-тканной капсулой. Для описания возникновения фиброзной капсулы воспользуемся критерием энергии формоизменения – критерием Мизеса:

с =

( ^С 1 — ^С 2 ) 2 + ( ° 2 ^-с 3 ) 2 + ^{( с} з ^-с 1 ) 2

Согласно этому критерию изменение состояния материала (микротравмирование) происходит при превышении некоторого предельного значения удельной потенциальной энергии формоизменения, которое определяется только физическими свойствами материала и не зависит от схемы напряженного состояния.

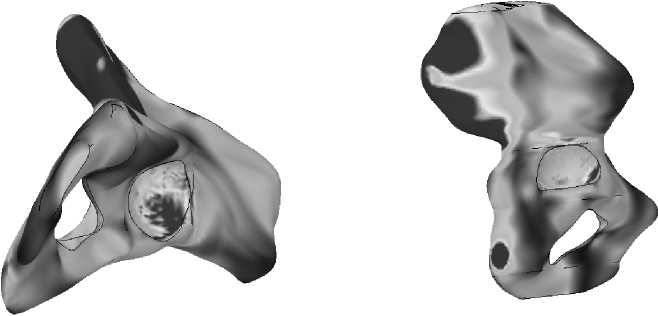
Результаты расчета напряженно-деформированного состояния тазовой кости во время переднего и заднего толчка приведены на рис. 30–31 .

3,7

а

0,0

б

Рис. 30. Картина распределения удельной потенциальной энергии формоизменения при переднем толчке: а – вид снизу, б – вид сбоку.

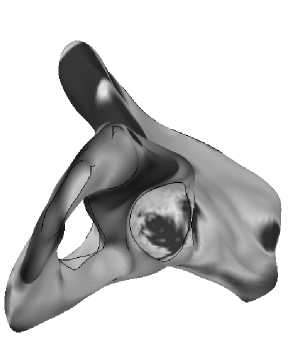
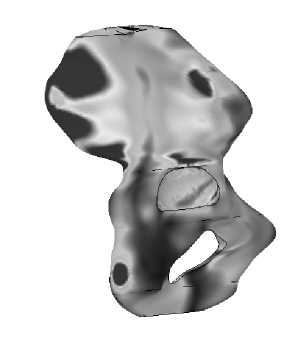
3,7

0,0

а

б

Рис. 31. Картина распределения удельной потенциальной энергии формоизменения при заднем толчке: а – вид снизу, б – вид сбоку.

3,7

0,0

II

III

Рис. 32. Распределение удельной потенциальной энергии формоизменения в кортикальной кости вокруг ножки имплантата во время переднего толчка (медиальный край).

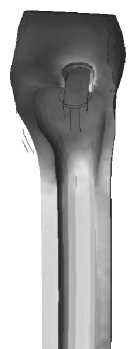
3,7

0,0

I

II

III

Рис. 33. Распределение удельной потенциальной энергии формоизменения в кортикальной кости вокруг ножки имплантата во время переднего толчка (латеральный край).

3,7

0,0

III

I

II

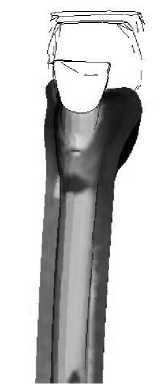
Рис. 34. Распределение удельной потенциальной энергии формоизменения в кортикальной кости вокруг ножки имплантата во время заднего толчка (медиальный край).

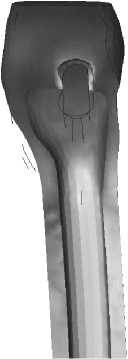
I

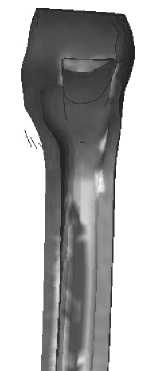
II

3,7

0,0

III

Рис. 35. Распределение удельной потенциальной энергии формоизменения в кортикальной кости вокруг ножки имплантата во время заднего толчка (латеральный край).

На рис. 32–35 представлено распределение удельной потенциальной энергии формоизменения на медиальной и латеральной границе контакта кость–имплантат для различных моделей эндопротезов во время переднего и заднего толчков соответственно.

Анализ приведённых на рис. 30-35 полей распределения удельной потенциальной энергии формоизменения показывает, что область и интенсивность микротравмирования кортикального слоя, характеризующие риск замещения кортикальной кости соединительно-тканной капсулой, различны для разных типов имплантатов. Так, эндопротез I типа характеризуется наименьшей зоной возможных микроразрушений, что вызвано малостью общей зоны контакта имплантата с кортикальной костью. Для модели эндопротеза II типа область возможных микроповреждений локализована в нижней и средней частях ножки имплантата с медиальной стороны и вдоль всей ножки имплантата с латеральной стороны. У модели имплантата III типа зона потенциального риска микроповреждений кости расположена в центральной зоне ножки имплантата. Данная модель эндопротеза имеет прямоугольную форму поперечного сечения ножки имплантата. Область контакта кортикальной кости с острыми углами эндопротеза также является зоной повышенного риска микротравмирования.

Заключение

Таким образом, при помощи построенной модели системы кость–эндопротез рассчитано напряженно-деформированное состояние костной ткани в наиболее нагруженные фазы шага. Выявлены участки кости с высокой концентрацией удельной потенциальной энергии формоизменения. Показано влияние конструкции эндопротеза на локализацию и интенсивность участков микротравмирования костной ткани, характеризующих риск замещения кортикальной кости соединительно-тканной капсулой. Предложенный алгоритм биомеханического исследования позволяет на этапе предоперационного планирования рассчитать возможные механические последствия выбора конструкции эндопротеза с учетом индивидуальных особенностей пациента.