Исследование напряженно-деформированного состояния кинематических опор А.К. Юсупова средствами ПК Лира-САПР

Эффективным средством сейсмозащиты зданий являются кинематические опоры (КО) [1, 2]. Указанные опоры эффективны при высокочастотных землетрясениях и, кроме того, дешевы благодаря простой технологии производства, позволяющей наладить их выпуск силами предприятий местной стройиндустрии. В работе А.К. Юсупова [2] приведены различные варианты КО в виде «кинематических стен» [3] (рис. 1). Моделирование работы собственно КО в [1, 2] осуществляется средствами теоретической механики без учета деформируемости опоры.

Целью настоящей работы является исследование напряженно-деформированного состояния трех КО А.К. Юсупова (условно обозначенных в таблице 1 как k 1 , k 4 , k 5 ) с использованием расчетной схемы, реализующей взаимодействие опоры с элементами конструкции здания как контактное взаимодействие с трением.

1 - 1

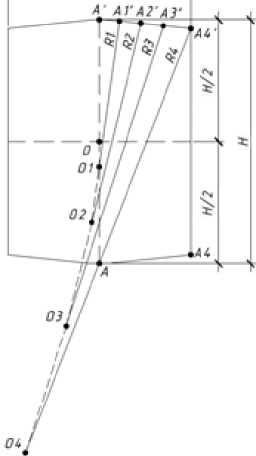
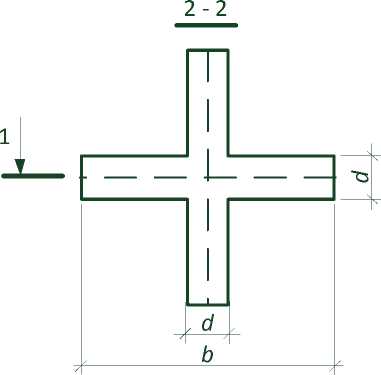
Рисунок 1 – Геометрия кинематических опор

Расчеты проводились в ПК ЛИРА-САПР. При реализации такой модели КО в ПК ЛИРА возникают определенные сложности. К ним в первую очередь относится неопределенность в назначении продольной и поперечной жесткостей двухузлового КЭ264. Указанные жесткости определяют контактное взаимодействие по нормали и по касательной к поверхности контакта. Кроме того, известные трудности возникают при назначении пользователем параметров итерационного процесса при решении конструктивно нелинейных задач.

Конечно-элементная модель опоры

Геометрия верхней и нижней контактных поверхностей КО определяется длинами V и радиусами R. дуг окружностей на участках i = 1 (между точками А и А1 (рис. 1)), i = 2 (между точками А1, А2) и т.д. Параметры контактных поверхностей представлены в таблице 1, где

Г см = 1,525 33/ 0,0739 - 10 — 6 F - (1) радиус смятия [2], определяющий размеры зоны контакта КО с обвязками, при действии вертикальной нагрузки F от веса здания в отсутствии сейсмического воздействия. Согласно рекомендациям [2] толщина стен КО принята равной 40 см, толщина и высота обвязки – 70 и 30 см соответственно.

Верхняя и нижняя обвязки, а также тело КО моделируются универсальным четырехугольным КЭ оболочки КЭ44 размерами 0,02 х 0,02 м. Характеристики материала: модуль упругости тела опоры E = 3•10⁷ кН/м²; коэффициент Пуассона v = 0,2; удельный вес R₀ = 25 кН/м³. Для нижних узлов нижней обвязки запрещены линейные и угловые перемещения по осям X, Y, Z. Для узлов верхней обвязки объединены линейные и угловые перемещения по X, Y, Z. Это сделано для того, чтобы обвязка деформировалась как единое целое в составе жесткого диска перекрытия.

Зона контакта опоры с обвязками моделируется при помощи КЭ264 (двухузловой односторонний элемент трения). Характеристики КЭ 264: осевая жесткость R = 1,01 • 10⁵ кН/м;

коэффициент трения ц = 0,7 - для пары материалов бетон - бетон [4]; жесткость сцепления Н_с = цН = 7,07 • 10⁴ кН/м; тип работы элемента - на сжатие.

Осевая жесткость R подобрана таким образом, чтобы фактический радиус смятия г_см от действия только вертикальной нагрузки при расчете в ПК ЛИРА-САПР соответствовал радиусу смятия, рассчитанному по формуле (1).

Для КЭ264 задаются зазоры: для центрального элемента зазор равен нулю; к периферии зазоры увеличиваются, следуя очертаниям поверхности контакта.

Конечно-элементная модель опоры представлена на рисунке 2 а в аксонометрии, на рисунке 2 б – в плоскости xz (плоскости действия горизонтальной силы).

Таблица 1

Геометрия контактной поверхности и размеры КО

КО	Номер участка (рис. 1)	Длина дуги участка V (см)	Радиус кривизны участка R i (см)	H (см)	b (см)
k 1	1	r + 7 см	151	300	230
	2	3	200
	3	2	600
	4	оставшийся участок	1800
k 4	1	r + 7 см	151	300	300
	2	3	400
	3	2	2000
	4	оставшийся участок	5000
k 5	1	r + 7 см	155	300	230
	2	3	300
	3	2	1500
	4	оставшийся участок	∞

Определение расчетных нагрузок на КО трехэтажного здания с цоколем

Рассматриваемое здание имеет высоту 1-3 этажа 3,6 м, шаг колонн 6 м (в продольном и поперечном направлениях), высоту цокольного этажа 3 м. Материал несущих конструкций – сборный железобетон. Сечение колонн - 400x400 мм; сечение ригелей - 500x300 мм. Расчетную схему принимаем в виде плоской поперечной рамы. Нижние узлы колонн цокольного этажа защемлены. В поперечном направлении рама имеет 4 пролета.

z _y

F

H

б

Рисунок 2 – Конечно-элементная модель кинематической опоры

Для типового этажа нагрузка на поперечную раму: распределенная постоянная равна 35,276 кН/м; постоянная сосредоточенная нагрузка (от стеновых панелей и остекления) – 42,096 кН; временная распределенная нагрузка (жилые помещения) – 11,482 кН/м.

Для покрытия распределенная нагрузка на поперечную раму составляет 26,461 кН/м . Расчет поперечной рамы производим в программном комплексе ЛИРА-САПР 2013 (ПК ЛИРА-САПР) согласно [5].

Параметры расчета на сейсмическое воздействие приняты следующими: поправочный коэффициент для сейсмических сил равен 1; тип сооружения - 1; Категория грунта G = 2; сейсмичность площадки в баллах S = 9 . Коэффициенты из таблиц СП 14.13330.2011: Ko = 1 (табл. 3); KA = 1 (табл. 4); K 1 = 0,35 (табл. 5); Kpsi = 1,30 (табл. 6). Направляющие косинусы равнодействующей сейсмического воздействия в ОСК: CX = 1; CY = 0; CZ = 0.

По итогам расчета рамы без сейсмоизоляции определены максимальные усилия в уровне верха нижних колонн: продольная сила F = 1218 кН; поперечная сила H = 268 кН.

При использовании сейсмоизоляции кинематические опоры устанавливаются вместо колонн в цокольном этаже. Поэтому для расчета КО в качестве нагрузки возьмем усилия, возникающие в уровне верха колонн цоколя. Продольная сила рассматривается как нагрузка, действующая на КО от веса конструкций здания. Поперечная сила соответствует величине максимального сейсмического воздействия на КО.

Напряженно-деформированное состояние кинематических опор 3-этажного здания

При статическом расчете КО нагрузка прикладывается к центральному узлу верхней обвязки. При такой нагрузке за счет наклона опоры в сторону действия горизонтальной силы Н в контакте с верхней и нижней обвязкой находится только одна из двух плит опоры (та, что лежит в плоскости действия силы).

Результаты расчета опоры k представлены на рисунке 3. Величины контактных напряжений по нормали к поверхности контакта опоры и обвязок (верхней и нижней) показаны на рисунке 3 а. Наибольшее напряжение оказалось равным 12,58 мПа. Равнодействующая этих напряжений оказалась равной F = 1229 кН. Это может послужить проверкой точности полученного приближенного решения, поскольку сила F должна уравновесить верхнюю обвязку, на которую действует вертикальная сила в 1218 кН. Таким образом, погрешность определения контактных нормальных сил взаимодействия составляет (1229 — 1218)/1218 - 100 = 0,9%, что вполне приемлемо.

Равнодействующие F приложены по обе стороны от оси симметрии КО на расстоянии 32,5 см и составляют пару сил, представляющих собой восстанавливающий момент (момент, стремящийся возвратить опору в первоначальное положение) M = 1229 - 0,325 - 2 = 799 кНм.

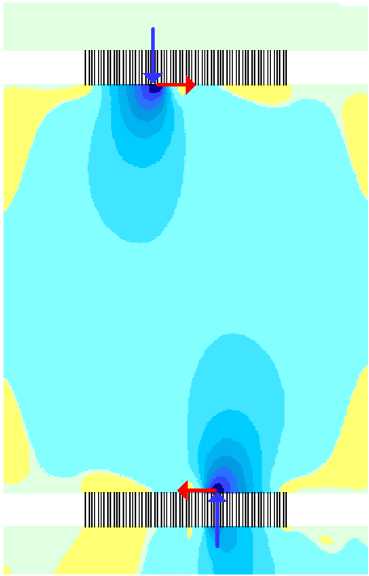
На рисунке 3 б показаны изолинии нормальных напряжений < г_г в опоре.

На рисунке 3 в показаны силы трения, возникающие в зоне контакта между узлами обвязок и опоры КЭ-модели. По горизонтальной оси отложены номера контактных пар узлов в зоне контакта. Все узлы в зоне контакта находятся в состоянии допредельного трения (проскальзывание отсутствует). Наибольшая сила равна 33,99 кН.

Равнодействующая касательных (к поверхности контакта) контактных сил взаимодействия F_x = 269 кН. Это также служит проверкой точности полученного приближенного решения: сила F должна уравновесить верхнюю обвязку, на которую действует горизонтальная сила в 268 кН. Таким образом, погрешность определения контактных касательных сил взаимодействия составляет 0,4%.

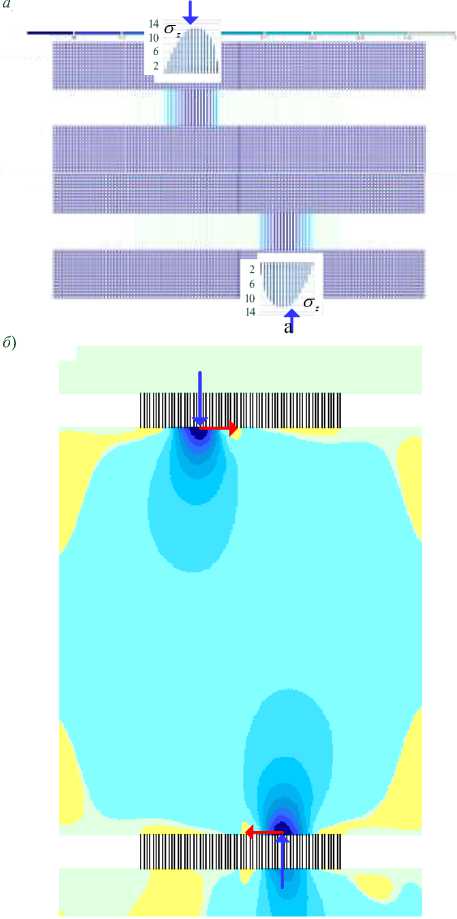
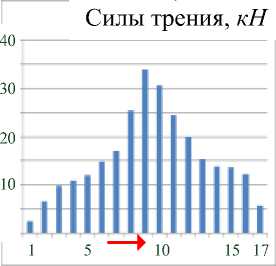
в

Рисунок 3 – Напряженное состояние опоры с кривизной k 1 для 3-этажного здания

Равнодействующие F составляют пару сил, представляющих собой опрокидывающий момент (момент, стремящийся опрокинуть опору) М_х = 269 - 3 = 807 кНм. Таким образом, опрокидывающий и восстанавливающий моменты уравновешены с погрешностью в 1%.

Отметим, что параметры итерационного процесса (число шагов по нагрузке и число итераций на шаге) во всех расчетах подбирались именно из условия выполнения рассмотренных выше уравнений равновесия.

На рисунках 4, 5 показаны аналогичные результаты для опор k , k .

б

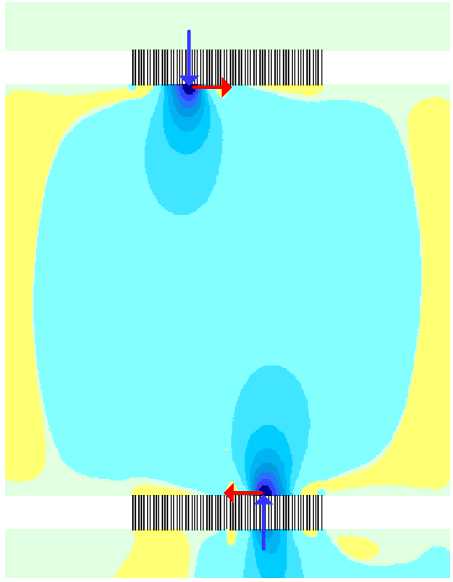
б

Силы трения, кН

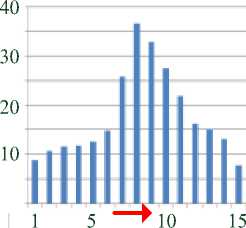
Рисунок 4 – Напряженное состояние опоры с кривизной k 5 для 3-этажного здания

в

Рисунок 5 – Напряженное состояние опоры с кривизной k4 для 3-этажного здания

Рассмотрим далее 5-этажное здание.

Определение расчетных нагрузок на КО 5-этажного здания с цоколем

Расчетные нагрузки на поперечную раму, материал конструкций и сечения элементов аналогичны таковым для трехэтажной рамы. По итогам сейсморасчета на 9-балльное землетрясение неизолированной рамы имеем следующие величины нагрузки на КО: максимальная вертикальная сила F = 1823 кН; максимальная горизонтальная сила H = 323 кН.

Напряженно-деформированное состояние кинематических опор 5-этажного здания

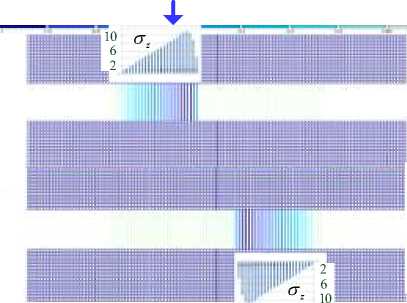
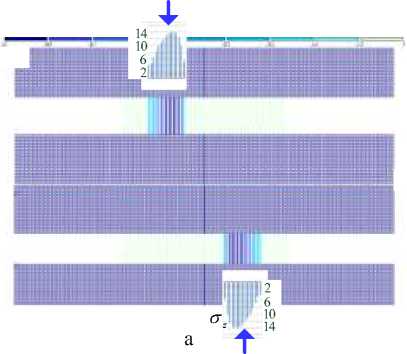
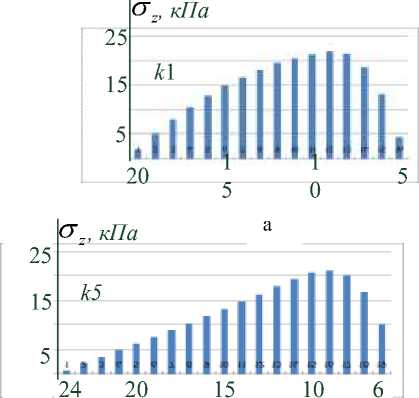
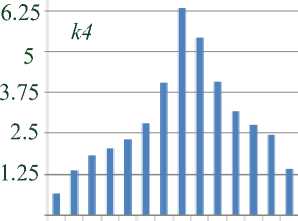
Качественно напряженно-деформированное состояние КО не отличается от такового для 3-этажного здания. Поэтому приведем лишь усилия контактного взаимодействия КО с верхней обвязкой. На рисунке 6 а, б, в показаны силы трения для опор k 1, k 2, k 3 соответственно. По горизонтальной оси отложены номера узлов конечно-элементной сетки КО (взаимодействующие с обвязкой), отсчитываемые от оси симметрии. На рисунке 7 а, б, в показаны напряжения σ по нормали к области контакта для тех же опор.

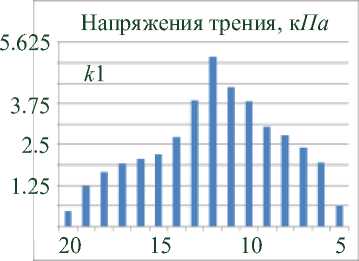
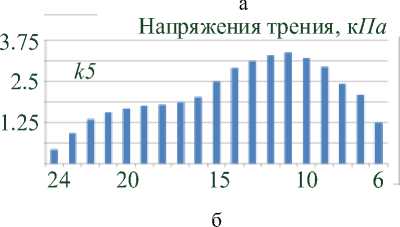
Напряжения трения, к Па

б

19     15       10      6

в

Рисунок 6 - Касательные контактные напряжения ( кПа ) между КО k 1, k 5, k 4 и верхней обвязкой для 5-этажного здания

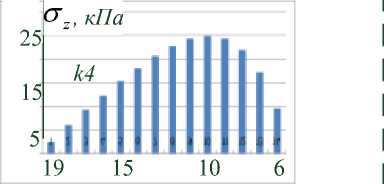
Рисунок 7 - Нормальные контактные напряжения ( кПа ) между КО k 1, k 5, k 4 и верхней обвязкой для 5-этажного здания

В таблице 2 приведено сравнение нормальных и касательных напряжений контактного взаимодействия КО с обвязками. Отметим неочевидное уменьшение размеров зоны контакта с ростом числа этажей. Величины контактных напряжений при этом увеличились.

«Всплеск» сил трения наблюдается на участке с наименьшей кривизной контактной (опорной) поверхности. Положение контактного давления максимальной величины не совпадает с максимальными силами трения. Отметим, что последние меньше предельных сил трения.

Таблица 2

Сравнение характеристик напряженного состояния в зоне контакта

КО	σ max , кПа	max τ тр , кПа	Размер зоны контакта, мм
3-этажное здание
k 1	12575	4148	340
k 5	11309	2068	480
k 4	14122	4581	300
5-этажное здание
k 1	21880	5184	320
k 5	21150	3376	380
k 4	24886	6318	280

Таким образом, в зоне контакта нет проскальзывания. Во всех случаях при принятой максимальной сейсмической силе наибольшие контактные усилия возникали на 4-м участке контактной поверхности КО (см. рис. 1, табл. 1).

Выводы

В статье рассматривается методика расчета в ПК ЛИРА-САПР кинематических опор, конструктивно выполненных в виде «кинематических стен», имеющих кроме перемещений за счет собственной деформации еще и поступательные и вращательные компоненты смещения как жесткого целого. Моделирование такой опоры приводит к необходимости решения контактной задачи с трением (конструктивно нелинейной задачи). Для обоснованного назначения жесткостных характеристик контактных элементов ПК ЛИРА-САПР требуется знание размеров зоны контакта для опоры, загруженной вертикальной нагрузкой от веса, лежащего выше здания. Жесткости контактного элемента подбираются численным экспериментом так, чтобы размеры зоны контакта оказались равными этим известным заранее размерам.

Исследовано напряженно-деформированное состояние трех видов кинематических опор А.К. Юсупова, отличающихся геометрией контактной поверхности. Даны рекомендации по назначению параметров итерационного процесса решения конструктивно нелинейных задач таких, что обеспечивается равновесие обвязки и кинематической опоры.