Исследование напряженного состояния вращающегося диска переменной толщины

Вращающиеся диски являются важнейшим элементом многих машин. Прочность и долговечность дисков определяют возможность получения высоких параметров работы машин, обеспечивают необходимый срок службы. Цель исследования ‒ разработать программу расчета быстро вращающихся дисков переменной толщины с учетом изменения температуры вдоль радиуса в САПР Mathcad и Фортран.

Объекты и методы исследования

Объектом исследования являются вращающиеся диски переменной толщины c изменяющейся температурой вдоль радиуса.

При выполнении работы использовано прямое интегрирование системы дифференциальных уравнений равновесия и совместности деформаций первого порядка численных методов [1]. Эти уравнения записываются относительно радиального усилия T^ ( r ) и радиального перемещения u ( r ):

и )     1 + v | и ]   1 - v1

- I =--I I +------ T 1 +

• r)      r I r ) Ehrr

, d     Eh (и)  1 - v Eh2

— T = —I — I--T--aAt - pro hr dr      r V r) r        r где T = тh [ — ] - интенсивность радиальных усилий;--окружная деформация; aAt -мr температурная деформация; h - толщина диска; р - плотность материала; ю - угловая скорость вращения; Е - модуль упругости; v - коэффициент Пуассона; а - коэффициент линейного расширения материала; At(r) - температура диска; т и т - радиальное и окружное напря- жения.

Переменные T 1 ( r ) и u(r) не претерпевают разрывов даже при скачкообразном изменении параметров диска (толщины, модуля упругости, температуры). При решении системы (1) будем пользоваться векторно-матричной символикой, которая позволяет компактно выполнить необходимые преобразования и составить программу. Систему разрешающих дифференциальных уравнений первого порядка можно представить в матричной форме:

-dy = Fy + g,                                     ⁽²⁾

dr

T где y = f-, T11

V r       )

‒ вектор состояния, с помощью которого в сечении диска (одномерной си- стемы) определяются все неизвестные обобщенные кинематические и силовые T1 факторы;

T ‒ знак транспонирования.

F =

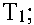
1 + v r Eh

r

1 - v ²

Ehr

1 - v —

r

‒ матрица коэффициентов, стоящих перед искомыми функциями ^u и

I 1 + v )

g =

r

Eh

a A t

0h)I

p_ro 2 - вектор свободных членов или вектор нагрузки диска.

V r )

Сила T2 в окружном сечении и напряжении a_r, т определяется по формулам:

T 2 = vT 1 + Eh I ^- - aA t V r

T 1

Tr = к h

T 2

T = — t_h

Решение системы (1) должно удовлетворять двум граничным условиям, которые заданы на внутренней (при r = r 1 ) и внешней (при r = r 2 ) поверхностях диска. Приведем некоторые варианты граничных условий:

• 1.    Внутренняя и наружная поверхности диска свободны от напряжений. В этом случае

• 2.    Диск посажен на вал с натягом A . При r = r i , и - - ь = ^, где -_ь - радиальное пере-

• 3.    На внутреннем контуре диска задано давление p , а на наружном контуре ‒ напряжение p , обусловленное растяжением лопаток. Тогда

• 4.    Диск без отверстия. Тогда при

при r = r 1    T 1 (r)=0 ,

при r = r 2

T 1 (r 2 )=0.

мещение вала на посадочной окружности. Если вал сплошной, то и_ь <  и (во много раз), и при

расчете можно пренебречь деформацией вала. В этом случае граничное условие имеет вид:

А u (r1) = -.

при r=ri T = - ph , при r = Г2 T = ph, где h1, h2 ‒ толщина диска на внутренней и внешней поверхностях соответственно.

r = 0 T = ^{Eh f} u - aA t ) ,

1 — V V -      J где u = 0, но u ‒ конечная величина; h0 ‒ толщина диска в центре. r

Так как коэффициенты в (1) при r =0 обращаются в бесконечность, то численный счет начинается в этом случае на небольшом расстоянии от центра ( A r = 10 ^— м ). При численном интегрировании системы (2) вектор состояния ' у' должен быть полностью задан.

Однако задача расчета диска принадлежит к классу краевых задач, т.е. в начальной точке интервала интегрирования заданы либо один из компонентов вектора состояния ' y ' (граничные условия 1, 3, 4), либо связь между компонентами (диск без отверстия). Эту трудность можно преодолеть, используя метод начальных параметров [2]. Согласно этому методу сначала проводят интегрирование однородной системы дифференциальных уравнений ( g = 0):

dry i = Fy i                                      ⁽⁴⁾

dr при начальном условии (начальном значении вектора состоянии) (y1(r1)). При этом, в силу линейности задачи, выражение C(y1(r)), где с ‒ постоянная, также является решением системы (4). Далее выполняют интегрирование неоднородной системы (2) при начальном условии y0(r1) ‒ частное решение системы (2). Полное решение может быть представлено как сумма полученных решений:

y ^{( r} ) = cy 1 ^{( r} ) + y 0 ^{( r} ) ,                                          ⁽⁵⁾

причем векторы состояния y 1 (r) и y 0 (r) задают таким образом, чтобы полный вектор состояния У ( r ) удовлетворял граничному условию при r = r i для любого значения с . Так, для рассмотренных ранее случаев граничных условий 1, 2, 3, 4 векторы состояния y 1 (r 1 ) и y 0 (r 1 ) имеют вид:

1 . 2 .	y 1 (- 1 ) = ( 1 , 0 )Т y 1 (Г 1 ) = ( 0 , 1 ) T	y 0 (Г 1 ) = ( 0 , 0 )T y 0 (- 1 ) = ( ^ , 0 )T 2 r 1
3 .	y 1 (Г 1 ) = ( 1 , 0 ) T	y 0 (r 1 ) = ( 0 , — P 1 h 1 ) T
4 .	y 1 (Г 1 ) = ( 1 , Eh 0 ) T 1 — v	y 0 (- 1 ) = ( 0 , 0 )T	- 1 = A r

Затем, подчиняя полученный вектор состояния y ( r ) граничному условию при r = r ^, определяем постоянную интегрирования с . Например, для случая 1 получим алгебраическое уравнение относительно постоянной с :

СУ(Г2)2,1 + y(r2)2,0 = 0,

^{где y(r}2 ) 2,1   ^Т ( ^Г2 )Ы     ^у ( ^Г2 ) 2,0   ^Т(г2 ) 1,0^.

Здесь индексы указывают: первый ‒ соответствует второму компоненту вектора состояния; второй: 1 ‒ общее решение однородной системы (4); 0 ‒ частное решение неоднородной системы (2). Таким образом, зависимость y ( r^ )₂₁ = T получена в результате решения однородной системы (4) при начальном значении r = Г 2 , а y ( r )_{2 0} = Т_х получена в результате решения неоднородной системы (1) при r = r 2 . В данном случае постоянная С равна окружной деформации ^ ₂ на внутреннем контуре диска.

Итак, в результате выполненных процедур вектор состояния в начальном сечении r = r 1 известен полностью:

y⁽r i ) = ^сУ 1 ^(г 1 ) + У о ^(г 1 ).

Интегрируя систему (2) с начальным вектором состояния (6), получают вектор состояния в любом сечении диска. При этом интегрировании производятся обработка результатов счета и вывод на печать необходимой информации (толщина, температура, вектор состояния, напряжения ст_г , ^ и т.д.) в характерных точках интервала интегрирования.

Для разработки и отладки программы расчета рассмотрим численный пример определения напряжений в диске переменной толщины (рис. 1 a) при вращении и неравномерном нагреве. Закон изменения температуры по радиусу дан на рисунке 1 с. Исходные данные: n б := 14500 об- р := 8 -103 кг- а := 1,2 • 10—5-1 v:= 0,3 px := 15 МПа - контактное давле- р         мин           м 3              c ние; р2 := 140МПа - интенсивность нагрузки на наружном контуре (инерционная нагрузка от лопаток) при рабочем числе оборотов E:= [1,8-105 -1,25-102(t-158-0)]МПа , r := 19 мм r := 36 мм   r := 140 мм r := 146 мм  hx := 52 мм h2 := 30 мм h3 := 18 мм h4 := 22 мм об n := 14500---- to := 1500c"1    r := 0,0.001..0.146

мин

Напряженное состояние в диске ‒ плоское. Напряжения распределены равномерно по толщине диска. Расчеты ведутся на алгоритмических языках Mathcad и Фортран [3, 4].

Программа определения h ( r )

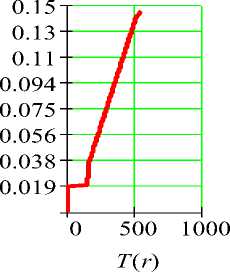
Программа определения T ( r )

h ( r ) : =

h if 0 <  r <  r₂

— h-------(Г3 — r) + hз if r2 < r < Г3

Г 150...

if 0 <  r <  r

L r 3 ^— r 2

h ₄ if r₃ <  r <  r ₄

T ( r ) : =

+ 892.9( r — r )

165...

+ 3311( r — r )

510...

+ 6667( r — r )

if r <  r <  r

if r <  r <  r

if r <  r <  r

Эпюры h(r) и T(r), построенные при помощи данных программ, представлены на рисунке 1 б, в.

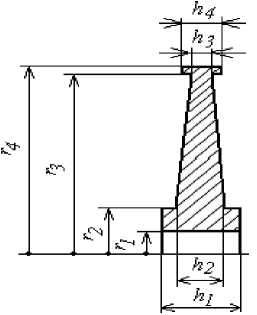
a

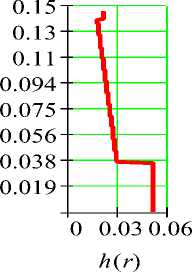
б

в

Рисунок 1 ‒ a ‒ расчетная схема диска переменной толщины и графики изменения; б ‒ толщины; в ‒ температуры вдоль радиуса диска

Программа расчета неравномерно нагретых дисков переменной толщины

Program DISK;                         1

Uses crt;

Label11;

N=2; NR=1450; R0=8E3;

AL=12e-6; Cp=0.3;

TYPE

Wect=array[1..4] of real;

Var

Ns, Ni, Ip, I, Np, Kp : integer;

• H,    x, Tx, Thx, Ex, Ur, T2, Sig1,

Sig2, C, C2:real; Y, XS: wect;

NN,KR; array[1..3] of integer;

{Вычисление температуры в зависимости от радиуса}

Function T(x:real):real;

Begin

If Ns=1 then T:=150+892.9*(x-0.019)

If Ns=2 then T:=165+3311*(x-0.0358);

If Ns=3 then T:=510+6667*(x-0.140);

End;

{Вычисление толщины в зависимости от радиуса}

Function TH(x:real):real;

Begin

If Ns=1 then TH:=0.052;

If Ns=2 then TH:=0.03-0.006*(x-0.0358)/0.052;

If Ns=3 then TH:=0.022;

End;

{Вычисление модуля упругости в зависимости от радиуса}

Function E(x:real):real;

Procedure RK(Var x:real; Var Y:wect, H:real); 3 Var

• I:    byte, Y1, P0,P2,P3: wect;

  Begin                             2

  E:=1.8E11-1.25E8*(T(x)-150);

  End;

  {Процедура вычисления правых частей дифференциальных уравнений} Procedure FCT(x:real; Y:wect; var P:wect);

  Var

  OM, ALT, CPP,CPM,

  TE,XX,A11,A12,A21,A22,G1,G2,SG :real;

  Begin

  OM:=3.1416*RN/30;

  ALT:=AL*T(x);

  CPP:=1+CP;

  CPM:=1-CP;

  TE:=E(x)*TH(x);

  XX:=1/x;

  A11:=CPP*XX;

  A12:=A11*CPM/TE

  A21:=TE*XX;

  A22:=CPM*XX;

  G1:=A11*ALT;

  G2:=A21*A1T+RO*TH(x)*OM**OM *X;

  SG:=1;

  If NI=1 then SG:=0;

  P[1]:=-A11*Y[1]+A12*Y[2]+SG*G1;

  P[2]:=A21*Y[1]-A22*Y[2]4-SG*G2;

  End;

  {Процедура интегрирования системы дифференциальных уравнений методом Рунге-Кутта}

  for Ni:= 1 to 3 do                4

  Writeln;

  
  

Begin

FCT(x, Y, P0);

For i:=1 to N do

Y1[i]:=Y[i]+H*P0[i]/2;

FCT:=(x+H/2, Y1, P1);

For i:=1 to N do

Y1[i]:=Y[i]+H*P1[i]/2;

FCT:=(x+H/2,Y1,P2);

For i:=1 to N do

Y1[i]:=Y[i]+H*P2[i]/2;

FCT:=(x+H,Y1,P3);

For i:=1 to N do

Y1[i]:=Y[i]+H*(P0[i]+2*P1[i]+2*P2[i]+P3[i]/6;

x:=x+H;

End;

Clrscr;

XS[1]:=0.019; XS[2]:=0.0358;

XS[3]:=0.14; XS[4]:=0.146;

Y1[i]:=Y[i]+H*(P0[i]+2*P1[i]+2*P2[i]+P3[i])/6;

x:=x+H;

End;

Begin

Clrscr;

XS[1]:=0.019; XS[2]:=0.0358;

XS[3]:=0.14; XS[4]:=0.146;

NN[1]:=16; NN[2]:=96; NN[3]:=6;

KR[1]:=4; KR[2]:=6; KR[3]:=2;

Y[1]:=1; Y[2]:=0;

Writeln( ' R ' , ' H ' , ' T ' , ' E ', ' U ' , ' T1 ', ' T2', '

SIG1 ' , ' SIG2 ' );

Writeln;

Writeln (' (м) ', '(м) ' , ' (гр) ', '(Па)', '(м)', '(Н/м)', '(Па)', '(МПа)', '(МПа)');

{Задание начальных условий}

Begin if Ni = 2 then Y[1]:= 0;

if Ni = 3 then Y[1]:= c;

if Ni >  1 then Y[2]:= - 78E4;

for Ns:= 1 to 3 do begin

X:= XS[Ns];

H:= (XS[Ns + 1] - XS[Ns]) / NN[Ns];

Np:= NN[Ns] div KR[Ns];

Kp:= KR[Ns] + 1;

for Ip:= 1 to Kp do begin if Ni < 3 then goto 1;

Tx:= T(x); Thx:= TH(x);

Ex:= E(x); Ur:= Y[1]*x;

T2:= Cp*Y[2] + Ex*THx*(Y[1] - AL*Tx);

Sig1:= Y[2] / Thx;

Sig2:= T2 / Thx;

Writeln (x: 6: 4, Thx: 7: 3, Tx: 6: 0, ' ' , Ex:

9 , ' ' , Ur: 9 , ' ' , Y[2]: 9 ,

' ' , T2: 9 , Sig1 / 1E6: 6: 0 , Sig2 / 1E6: 6: 0);

if Ip < Kp then for I:= 1 to Np do Rk(x, Y, H) else end; end;

{Вычисление постоянных интегрирования} if Ni = 1 then C2:= Y[2];

if Ni = 2 then C:= (3.08E6-Y[2]) / C2;

end;

Readln;

END.

По полученным результатам счета построены эпюры напряжений т и т (рис. 2).

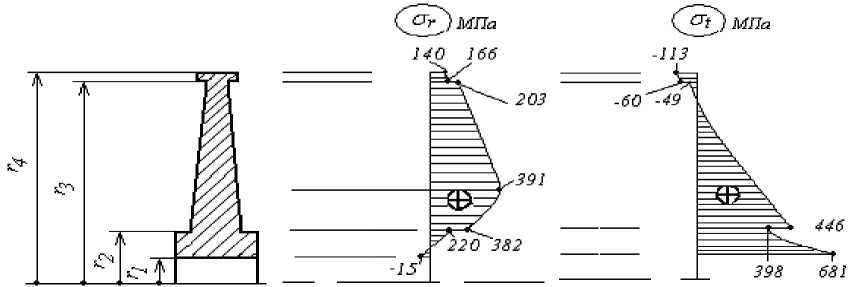
Рисунок 2 ‒ Эпюры радиальных и окружных напряжений в диске при рабочем числе оборотов

Выводы

Таким образом, разработанная программа расчета быстро вращающихся дисков переменной толщины с учетом изменения температуры вдоль радиуса в САПР Mathcad и Фортран позволяет при любых значениях исходных данных: 1) исследовать напряженное состояние диска; 2) проверить прочность диска при рабочем числе оборотов по любой теории прочности; 3) увидеть, как программы выполняют расчет в естественной последовательности и представляют в наглядном виде результаты счета; 4) по разработанной программе можно определить контактное давление p между валом и диском, а также найти натяг Δ при любом числе оборотов, обеспечивающем требуемое контактное давление p _{k ω} = p _{k ω . adm} .