Исследование незамкнутой адаптивной гидростатической опоры с независимым плавающим регулятором

В тяжелом и прецизионном станкостроении, а также в других областях техники широкое применение находят адаптивные гидростатические опоры и направляющие с плавающими регуляторами расхода в магистрали нагнетания рабочей жидкости [1; 2]. По сравнению с мембранными плавающие регуляторы позволяют обеспечить опоре более стабильные характеристики и имеют значительно меньшие габаритные размеры, благодаря чему их можно встраивать непосредственно в неподвижное основание направляющей.

В отличие от известных и ранее исследованных незамкнутых опор с плавающими регуляторами [3], опоры с независимыми плавающими регуляторами способны обеспечить необходимую податливость несущего смазочного слоя без дополнительного (точнее – сведенного к минимуму) потока рабочей жидкости, поддерживающего плавающее рабочее состояние подвижного элемента (плунжера) регулятора. Следовательно, они отличаются значительно более высокой экономичностью.

Кроме того, отсутствие дополнительного ограничения перемещения плунжера при возрастании нагружения позволяет существенно улучшить нагрузочную характеристику адаптивной опоры [3].

Незамкнутые адаптивные гидростатические опоры с независимыми плавающими регуляторами для направляющих могут быть выполнены в двух основных вариантах: либо с внутренним, либо с периферийным (внешним) входным дросселированием регулятора (рис. 1).

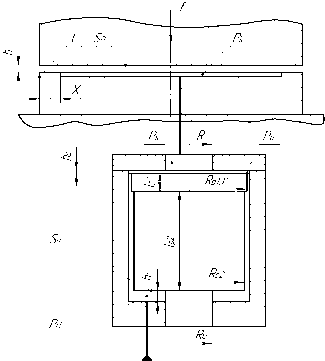
Рис. 1. Расчетная схема незамкнутой адаптивной гидростатической опоры, имеющей независимый плавающий регулятор с периферийным дросселированием [4]

Регуляторы имеют входные дроссели, образованные двумя дросселирующими ступенями шириной l₁ = l_{p 1} и l_p 2 с радиальными зазорами (на рис. 1 они не обозначены), обеспечивающими радиальное центрирование верхней части регулятора, и управляемую дросселирующую щель с рабочим зазором h p , необходимую для активного регулирования расхода.

Математическая модель стационарного нагружения опоры является системой четырех алгебраических уравнений:

h 3 -Р к = h L ^ J P p ^- P к ) , ⁽¹⁾ x ^p ( - In R )

hp In T?(Pк Pp ) h1 2/ (pн pp ), n1

pp + Kppк = K ' pн ,

Pк5о = f , где Рк – давление в несущем кармане опоры; Рp – давление на входе в управляемую дросселирующую щель s регулятора; Pн - давление нагнетания; Kp = -вых-, p sвх здесь sвх и sвых – входная и выходная эффективные площади торцевой рабочей поверхности регулятора;

s

K = —— , здесь 5н - площадь силового замыкания s вх регулятора, т. е. торцевой поверхности, на которую действует давление pн ; sо – несущая эффективная площадь гидростатической опоры; h – рабочий зазор опоры; h1 и l1 = lpi - радиальный зазор и ширина дросселирующей цилиндрической ступени (меньшего зазора) регулятора, определенные из условия равенства сопротивлений центрирующих ступеней; l и x – длина и ширина дросселирующих перемычек опоры, т. е. питаемого несущего кармана направляющей; R – отношение радиуса кармана или выходного отверстия регулятора к его внешнему радиусу r ;

f – внешняя нагрузка на опору с учетом веса приведенной к опоре подвижной части направляющей.

Уравнения (1) и (2) являются нелинейными и представляют собой уравнения балансов расходов гидростатической опоры ее регулятора, а уравнения (3) и (4) являются линейными и выражают условия силового равновесия регулятора и гидростатической опоры.

Площадь торцевой поверхности регулятора, необходимая для его силового замыкания и уравновешивания, на которую действует давление нагнетания, может быть определена по дополнительному уравнению его равновесия в начальном (расчетном) нагруженном состоянии опоры:

pр0 + Kp pк0 = K'pн , где pк0 и pр0 – начальные (расчетные) значения дав- ления в несущем кармане опоры и на входе в торце- вую дросселирующую щель регулятора.

В результате решения краевой задачи применительно к стационарному уравнению Рейнольдса для радиального течения рабочей жидкости в тонком дросселирующем слое и последующих преобразований было получено используемое в уравнении (3) отношение выходной и входной эффективных площадей рабочей торцевой дросселирующей поверхности ре- гулятора:

5 _Вых        R ² — 1

вых

" 5 _вх ~2ln R - R ² +1,

которое является справедливым для направления течения рабочей жидкости от периферии торцевой дросселирующей щели к ее центру.

Выполненные на основе математической модели (1)-(5) расчеты показали, что при K > 1 и малой внешней нагрузке f система уравнений (1)–(4) не имеет приемлемого с точки зрения реально допустимых значений параметров опоры решения, что указывает на наличие ограничения активного рабочего на- грузочного диапазона опоры нижним предельным значением нагрузки, т. е. ограничения снизу.

Тем не менее математическая модель (1)–(5) вполне доступна для алгебраических преобразований, благодаря чему мы можем провести более подробное исследование.

Из (2) имеем

h ³ p

_ 3 r In R • ( ^P „ ^{- P} p )

= ^h 1                 \

1 к —

Подставим это выражение в следуемое из (1) выражение рабочего зазора гидростатической опоры:

h - . h''( pP - p к ) .

^p l (^- ln ^R ) р к

h 3 r ln R ( P н ^- P p ) ^{2 n x} ( P p ^- P k ) ¹ 2A ( P к - P p )     ^{l ( -} ln ^R ) P k

= h ^-

r K x ( P н ^-

p p

l l l ' P к

Приняв p _р = K * p _н - K _p p _K, получим

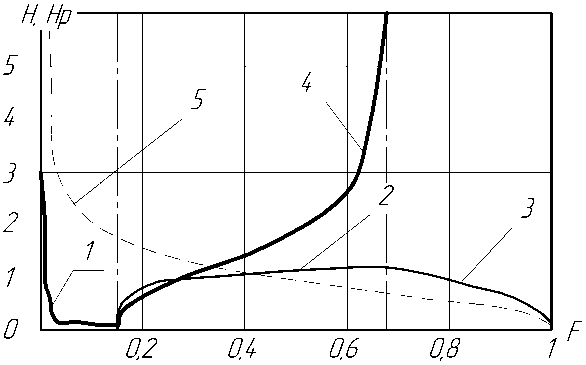
Рис. 2. Нагрузочные характеристики незамкнутой адаптивной опоры (линия 1 – нижний пассивный диапазон;

2 – активный диапазон нагружения; 3 – верхний пассивный диапазон), плавающего регулятора (линия 4 ) и пассивной гидростатической опоры с постоянным входным дросселем

(линия 5 ) при K = 1,38

Используя выражения (5) и (4), окончательно имеем

n rx h = h 3

¹      l ₁ l

^ о P н ( 1 ^{- K} ) +     R ² - 1

f      2ln R - R ² + 1

.

Эта формула позволяет рассчитать нагрузочную характеристику опоры в активном диапазоне, соответствующем плавающему (подвижному) состоянию плунжера.

Анализ формулы (6) показывает, что при K = 1, т. е. при равенстве площади силового замыкания регулятора его входной эффективной площади, первый член подкоренного выражения формулы (6) обращается в нуль и в этом случае рабочий зазор опоры не зависит от внешней нагрузки, т. е. опора будет иметь нулевую податливость. Кроме того, из формулы (6) следует, что при K = 1 податливость опоры не зависит от подводимого давления нагнетания p _н и несущей эффективной площади опоры (направляющей) s _о .

При K >  1 увеличение нагрузки уменьшает значение рабочего зазора и, следовательно, опора может иметь отрицательную податливость. При этом с увеличением K (в пределе до 5...10) отрицательная податливость становится значительно более существенной, однако при этом активный диапазон нагружения неуклонно сокращается.

При K <  1, напротив, увеличение нагрузки повышает значение рабочего зазора и, следовательно, опора обладает положительной податливостью, возрастающей с уменьшением K . Тем не менее положительная податливость исследуемой опоры в этом диапазоне значений K существенно меньше податливости гидростатической опоры, имеющей входные дроссели постоянного сопротивления, поскольку плавающий элемент регулятора при нагружении опоры остается подвижным и возникает активное регулирование расхода рабочей жидкости.

Проверить справедливость формулы (6) позволяет нагрузочная характеристика исследуемой опоры, показанная на рис. 2, адаптивный диапазон которой рассчитан по безразмерному аналогу математической модели (1)–(5).

Расчет и построение нагрузочной характеристики производились следующим образом.

Сначала определялся адаптивный диапазон нагружения, где в качестве исходной расчетной точки использовалась точка в средней части диапазона, соответствующая пересечению кривых перемещений опоры и регулятора, поскольку начальные настроечные значения безразмерных зазоров опоры H = h/h ₀ и регулятора H _p = h _p hh _p0 принимались равными единице.

Затем с малым шагом варьировалось давление в несущем кармане опоры (нагрузка) с отступлением от исходной точки как в сторону увеличения давления, так и в сторону его уменьшения. При этом было обнаружено, что уменьшение давления на нижней границе диапазона вызывает резкое уменьшение зазора опоры, вплоть до нуля, а увеличение давления при приближении к верхней границе диапазона – резкое возрастание зазора регулятора (теоретически – вплоть до бесконечности). В результате был сделан вывод о том, что оба эти явления способны вызвать неустойчивость и в связи с этим свободные плавающие перемещения подвижного элемента регулятора необходимо ограничить введением в его конструкцию дополнительных элементов – упоров, ограничивающих резкие перемещения.

После определения граничных точек активного диапазона были построены математические модели для пассивных диапазонов нагружения опоры с неподвижным регулятором (дросселем) и рассчитаны нижний и верхний пассивные нагрузочные диапазоны. Граничные точки пересечения диапазонов (точки бифуркации) по аналогии с замкнутыми опорами [2] были названы критическими.

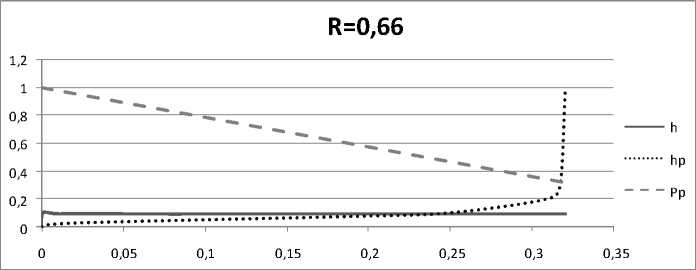
Результаты исследования позволяют сделать вывод, что при K <  1 нижний нагрузочный пассивный диапазон полностью исчезает, но опора при этом имеет положительную податливость. Этот вывод подтверждают нагрузочные характеристики для активного диапазона, показанные на рис. 3, которые были рассчитаны по безразмерным аналогам математической модели (4), (5) и формулы (6).

1,2

R=0,25

------h

0,8

0,6

0,4

0,2

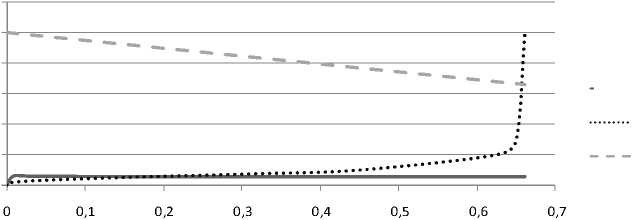
hp

Pp

Рис. 3. Активные диапазоны нагружения незамкнутой адаптивной опоры (горизональная линия), плавающего регулятора-стабилизатора (восходящая линия) и значения давления на входе в управляемую активную дросселирующую щель регулятора при K = 1,001

Кроме того, расчетные нагрузочные характеристики также показывают, что уменьшение R при близких к единице значениях K расширяет активный диапазон нагружения настолько, что регулятор может работать как стабилизатор практически во всем реальном диапазоне внешнего нагружения направляющей.

Таким образом, можно сделать следующие выводы:

– создание работоспособных конструкций незамкнутых адаптивных гидростатических опор с плавающими регуляторами, не имеющими дополнительных потоков рабочей жидкости, которые не поступают в несущий карман опоры, является возможным. Обязательным условием работоспособности таких опор в режиме отрицательной податливости является наличие пассивного нагрузочного диапазона в области небольших нагрузок (нижнего пассивного диапазона), обеспечиваемое наличием в конструкции регулятора специального граничного упора;

• – отношение площади силового замыкания регулятора к его входной эффективной площади – параметр K – является наиболее важной характеристикой независимых плавающих регуляторов незамкнутых адаптивных гидростатических опор (направляющих), которая главным образом и определяет их активность и вид нагрузочной характеристики;

• - при K <  0 регуляторы не обеспечивают опоре отрицательную податливость, но при этом они могут использоваться для стабилизации рабочего зазора опоры (как стабилизаторы) и ограничения расхода рабочей жидкости при противоположно направленной нагрузке. В этом случае нижний граничный упор в конструкции плавающего регулятора (стабилизатора), как правило, не нужен.