Исследование обобщенного неравенства Харди через системы нелинейных дифференциальных уравнений в весовом пространстве Лебега со смешанной нормой

В современной теории уравнений математической физики широко применяются функциональные методы, берущие начало из классических работ Д. Гильберта. При исследовании эллиптических уравнений важную роль играют теоремы вложения, изученные различными математиками [1]. Далее при исследовании теоремы вложения в произвольных открытых множествах появляется многомерный оператор Харди. А это в свою очередь требует оценить оператор в различных весовых функциональных пространствах. Среди этих пространств важное место занимает весовое пространство Лебега. Оценка, многомерного оператора. Харди в весовых пространствах Лебега, берет начало с работ [2] и [3]. С другой стороны, многомерный оператор Харди имеет приложения в спектральной теории операторов, в теории дифференциальных уравнений с частными производными, в теории интегральных уравнений, в теории функциональных пространств и др. (см. [4, 5, 10]). Поэтому получение оценки для многомерного оператора. Харди в пространстве Лебега, является актуальной задачей. В одномерном случае отметим известную монографию [11].

В работе доказывается связь системы нелинейных дифференциальных уравнений с двумерным оператором Харди в весовом пространстве Лебега, со смешанной нормой. Другими словами, доказывается, что весовые функции, участвующие в определении весового пространства. Лебега, со смешанной нормой, связывают эту систему с двумерным оператором Харди в этом пространстве.

Теперь перейдем к изложению некоторых обозначений и вспомогательных фактов. Пусть 1 < P i ,P 2 <  то 11 pi(t') — весовые функции. определенные на. (0, то), т. с. изме римые по Лебегу, почти всюду положительные и конечные функции на (0, то), i = 1, 2.

Предположим, что pi = p^-y и qi = qq—i , где i = 1, 2. Всюду в дальнейшем будем считать, что рассмотренные функции являются измеримыми по Лебегу. Пусть f : (0, то)² Н- R произвольная измеримая функция, где (0, то)² = (0, то) х (0, то). Определим весовое пространство Лебега со смешанной нормой. Это пространство обозначается через L(_P1,_P2,_P1,_P2) [(0, то)²] и состоит из функций, для которых конечна норма [6]

^  ^p2

Р1Р2

Ilf Hl^ ,p₂ _р₁,р₂)[(0,^)²] = I / I     If ⁽x1,x2⁾|^P1 Pi ^(xi) dxil   P2^(x2) dx2 I .

0^0                             ''

Через C ⁱ(0, то) обозначается пространство непрерывно дифференцируемых функций на (0, то). Множество всех абсолютно непрерывных функций на каждом компакте интервала (0, то) обозначавтся через AC ^loc(0, то).

2.    Формулировка основного результата

Пусть vi(t). wi(t) — весовые функции. определенные на. (0, то), vi Е C 1(0, то) 1i Ai > 0 — некоторые заданные числа, i = 1, 2. Рассмотрим систему обыкновенных нелинейных дифференциальных уравнений

Ai d ([vi(t)]p¹ [У1 (t)]p¹) + ^i(t)[yi(t)]p¹ =0, A2 ^ ( [V2(t)] q² [У2 (t)] p² ) + ^2(t)[y2 (t)] p² =0,

где yi(t) > 0, yi(t) > 0 (t > 0), yi(t) Е ACloc(0, то), i = 1, 2.                (2)

Под решением задачи (1)—(2), будем понимать пару функций (yi (t), У2 (t)), которая почти всюду на (0, то) удовлетворяет системе (1) и условию (2).

Основной теоремой работы является

Теорема 1. Пусть 1 < pi 6 qi < то, vi(t), wi(t) — весовые функции определенные на (0, то) 11 vi Е Cⁱ (0, то), где i = 1, 2. Тогда для разрешимости задачи (1)—(2). необходимо и достаточно, существование постоянной Co > 0 такой, что выполняется неравенство

HuHL(q1 ,q2,"1,"2) '"0-Х ^ 6 C02

d2u dxidx2

,

L(P1 ,P2,vi ,v2) ^[(0’^^)2]

где u : (0, то)² H- R — произвольная абсолютно непрерывная функция двух переменных, удовлетворяющая условию

u(xi, 0) = lim u(xi ,t2) = 0, t2^+0

Тогда, имеет место неравенство llUkL(qi ,q2 ,Ш1,Ш2)[(0,^)2 ] 6 ^l1 ^'22

d ² u dxidx₂

^L ( p i ,P 2 ,v i ,V 2) ^[(G ,^ ^)2]

где u : (0, to) ² H- R произвольная абсолютно непрерывная функция двух переменных, которая удовлетворяет условию (4).

C ных имеет место представление (см. [8, с. 246])

x 1                         x 2                         x 1 x 2

Г ^du(ai, ⁰⁾          Г ^du(0,a2)          Г Г ^d2u^(al,^a2)

u(xi,x2) = u(0, 0) +  — ---- dai + — ---- da2 +     —д—д---daida2. (6)

dai          J    da2         J J   da^da2

Очевидно, что из условий (4) следует u(0, 0) = lim u(ti,t2) = 0. Поэтому из равен-ti^+G, t2 > -G ства (6) в силу (4) по.тмчасм u(xi,x2) = Д R ^дааЮ2) daida2. Отметим, что последнее 0         «2

представление определяет двумерный оператор Харди [/]. Предположим, что функция y(x1,x2) = (y1(x1),y2(x2)) является решением задачи (1)-(2). Тогда в силу неравенства Гёльдера, имеем x1 x2

|u(xi,X2)|^qi Ш1

(^АП

G

G

д2и dt1dt2

q 1

dt₁dt₂ ш₁

x 1 x 2

(x1) 6 (Л

GG

д2и dt1dt2

q 1

Ш1(Х1)

x 1 x 2

=

GG

x 1 x 2 /(/

G

д 2 и dt1dt2

д 2и dt1dt2

¹            - ¹

[y0(t1)]Pi [y0(t1)] Pi

q 1

dt₁dt₂ I w₁(x₁)

- 10                        10         q1

[y 0 (t1)] ^pi dt2 ) [y1 (t1)]^pi dt1     Ш1(х1 )

x 1                  q ₁ x 1 x 2

⁶ 0 у^1№) dt1 )^pi CKte.

G                      G G

_- 1 ₀          p _{1         p} q 1 ₁

[У1 (t1)] ^Pi dt2     dt1      Ш1(Х1 )

6 Ш1(Х1) (У1(Х1))

x 1     x 2

q 1 ₀

p 1

GG

д2и dt1dt2

x 1     x 2

_d                 q ₁            ^q 1

= -А1 dX1 ([v1(x1)] pi [y0(x1)] Pi Д / GG

d2u dt1dt2

x 1                                                      p ₁      x 2

^q 1                ^q1 q

=         - A1        [V1(X1)] Pi [У1 (X1)]Pi           / dx1

GG

_- 1 ₀         p 1

[y0(t1)] Pi dt2 )

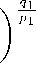
_- 1 _{0         p 1        p} q 1 ₁

[y₁ (t1)] ^p i dt2 dt1

д 2 u dt1 dt2

[У1 (t1)]

Pi dt2

p 1

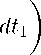
q ₁ p ₁

Интегрируя обе части неравенства (7) по переменной х1 и применяя обобщенное нера- венство Минковского, имеем

∞                          p ₁

q ₁

|u(xi, x₂)|^q 1 w_i(x_i ) dx_i

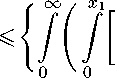
λ1 d dx1

p ₁ x 2

∂2u

∂t1 ∂t2

q1

- 10        p1        p1

[yi (ti)] p1 dt2j   dti Idxi

∞∞

0 t 1

∞ x 2

-Л/ 00

-

λ1 d dx1

∂2u

∂t1 ∂t2

∞   x 2

∂2u

∂t1 ∂t2

∞ x 2

= А*/(/

x 2

∞ p1        λ1 d dx1

[yi (ti)]

∂2u

∂t1∂t2

-

t 1

^p10 1 dt2

∂2u

∂t1 ∂t2

p 1

_- 1 ₀          q 1           q ₁

[yi(ti)] p¹ dt2j   dxi I    dti

p ₁

q1                q10                q1

[vi(xi)] p ¹ [yi (xi)] p ¹   dxi       dti

p ¹                     q ₁              ^q 1 ₀

Ai[vi (ti)] ~ [yi(ti)] p ¹

p ₁

q 1

dt1

p 1            _- ^p 1 ₀                     p ₁

dt2 I   [yi(ti)] p ¹ vi(ti)[y^,i(ti)] p¹ dti

∞   x 2

- >"/(/

Таким образом, получили неравенство

∞ 1 q ₁

|u(xi, x2)|q1 wi(xi) dxi I

∂2u

∂t1 ∂t2

p 1

v1 (ti) dt_i.

∞ x 2

λ1q11

∂2u

∂t1 ∂t2

dt2)p1 vi(ti) dti ) p1

.

Снова, применяя обобщенное неравенство Минковского, получаем

∞ x 2

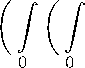
∂2u

∂t1 ∂t2

Таким образом,

x∞ p1                  p11        2

vi (ti) dti 6

∂2u

∂t1 ∂t2

p ¹

¹                    p ₁

vi (ti) dti      dt2.

∞ 1

q ₁

|u(x_i, x₂)|^q1 ш ₁( х ₁) dx_i I

x 2    ∞

6 λ₁^q1

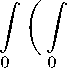
∂2u

∂t1∂t2

p ¹

¹                      p ₁

v_i (t_i) dt_i      dt₂ .

Далее, из последнего неравенства получим

∞                           q ₂

q ₁

|u(x_i, x₂)|^q1 ш ₁( х ₁) dx_i

x2   ∞ q2

Ш2(Х2) 6 A q ¹ Ш2(Х2)

∂2u

∂t1 ∂t2

Р 1

vi (ti ) dti

1 p ₁

q 2

dt2

Теперь оценим выражение w2(x2)( J^2 Jj^ I dti8t2 I  v1(t1) dt^ p1 dt2^  • Повторяя про цесс доказательства неравенства (7), имеем

x 2

/[ ^{— A}2

^x 2    ^∞

о

о

∂2u

∂t1 ∂t2

p ₂

_d                 q ₂            ^q 2      q ₂

( [v2(x2)] p2 [У1 (xi)] p2 )      ( dx2

p                  1

v1 (t1 ) dt1dt2

∞

О

∂2u

∂t1∂t2

Р1 .......-4, \Р2,

V1(t1 ) [У2(t2)] p ² dti       dt2

Поэтому

∞ q

2q q1                     q2

| u(xi, X2) | ^q1 ^1(xi) dxi ) W2(x2) 6 A q ¹

x 2

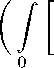
— A2

d dx2

q 2                ^q 2 0

[V2(X2)] p ² [У1 (xi)] p ²

p ₂ q ₂

∞

X

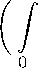
∂2u

∂t1 ∂t2

p 1                      _- 1 ₀

vi(ti)[y2(t2)] p ² dti

p ₂

p ₁

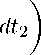
q ₂ p ₂

x2

неравенство Минковского, получим неравенство (5). B Положим

₀                                                                t                         _qi

Mi = p i inf sup-------M---------- [ ^i(s)(gi(s)) pi + ds, qi     t>0 gi(t) — J(v i (s))^1-p i ds 0

где инфимум берется по всем измеримым функциям gi таким, что для всех t >  0 gi(t) > J(vi(s))^1-pi ds, i = 1, 2.

„ 0                                                  .             _

Следующая лемма устанавливает связь задачи (1)-(2) с числами Mi (i = 1, 2).

Лемма 1. Пусть Ai > 0 — числа, заданные в теореме 1, и Mi — величины, определенные равенством (8), i = 1, 2. Предположим, что vi и л; весовые функции, определенные па (0, то ). II дл!I всех t € (0, то ) существует производная vi(t). Тогда (ледуюпше утверждения эквивалентны:

• (а)    если задача (1)—(2) имеет решение с локально абсолютно непрерывным производным первого порядка, то Ai > Mi;

• (b)    ее. тп Mi < + то , то за дача. (1)—(2) имеет решенае для каждого Ai >  Mi, i = 1, 2.

C Докажем пункт (а). Пусть y(t) = (y₁(t),y₂(t)) является решением задачи (1)-(2). Возьмем Wj = yi v¹ pi . Тогда (рлчпспия w ( t ) = ( wi ( t), w₂ ( t )) является положительным решением енет^ш

_< wi^(t) = 51Щ ^1^{(t) (}W1^(t)) p ¹ +¹ + ^[v1^(t)]1 p ¹, .^w2^(t) = qfc ^2^{(t) (w}2^(t)) p ^{2 +1} + ^[v2^(t)]1-p2.

Из (9) вытекает, что t

w i

(t) >/

w _i ⁰ (s) ds

t _q

= -pi- [ Wi(s)(wi (s)) pi + ds + q i λ i

t [v i (s)]^1-p i ds, 0

i = 1,2.

Из (10) получим wi ( t ) >  j [ v i( s )]¹ pi ds и

Xi > pi qi

t

t

Wi (t) - j(v i (s))¹ pi ds 0

j w i (s)(w i (s))

pi ⁺¹ ds.

Из (11) ii (8) вытекает, что X i >  Mi ii доказателг>ство пункта ( a ) завершено.

Теперь докажем пункт (b). Фиксируем числа X i >  Mi, i = 1,2. По определению величии Mi еушеетвутот лебеговы измеримые функции gi ( x i) такие, что

t                                         tq gi(t) > /‘(vi(s))1-pi ds + piv [ ^i(s)(wi(s)) pi+ ds, i = 1, 2.

q i λ i

Определим последовательность функций wn,_i(t) ii = 1, 2) следующим образом:

t

wo ,i (t) = g i (t),

t

W n +i ,i (t) = / (v i (s))¹ pi ds + -p i- /‘^ i (s)(w n,i (s)) pi ⁺ ds, n £ N . q i λ i

Из (12) вытекает, что wo,i(t) > wi,i(t). Положим w n

₁, _i(t) >  wni(t). Докажем, что

после-

довательности {wn,i(t)} и {wn,2(x)} являются убывающими. Имеем

t

wn,i(t) - wn+1,i(t) = -pi-    Wi(s) (w, qi λi

'n- 1 ,i (s)) ^p i ⁺¹

^^^^^^^^r

(w n,i (s)) pi ⁺

ds >  0.

Так как wn,i(t) >  0, то последовательности (13) сходятся. Обозначим их пределы че рез: w i (t). По теореме Леви о монотонной сходимости отсюда следует, что w i являются неотрицательными решениями уравнений

t

t

w i (t) = /‘(v i (s))¹ pi ds + p-д- /"w i (s)(w i (s)) pi + ds, i = 1, 2. q i λ i

Отсюда, получаем, что wi являются абсолютно непрерывными и удовлетворяют дифференциальным уравнениям wi(t) = (vi(t))1 pi + -pi- ^i(t)(wi(t))pi+ , i = 1, 2. qi λi

Поэтому функции

R [wi(s)]-1 (vi(s))1-pi ds yi(t) = eai                      , i = 1 2, удовлетворяют условиям задачи (l)-(2). B

Теорема 3. Пусть 1 < pi 6 qi < то, Mi < то и vi(t), ^i(t) — весовые функции, определенные на (0, то), где i = 1, 2. Предположим, что C > 0 наименьшая постоянная такая, что имеет место неравенство kukL(qi,q2,^2) |(0, X Л' 6 C q2

d²u dx ₁ dx ₂

,

L ( P 1 ,Р 2 >v i ,V 2) ^{[(0 ,x )}^^]

где u : (0, то ) ² Н- R — произвольная абсолютно непрерывная функция двух переменных, которая удовлетворяет условию (4). Тогда C 6 M₁ M2.

C Обозначим дИ2д1л = r(x1,x2)• Далее, при выполнении условий (4) получим u(x1 , x₂ ) = Л1 Л² r ( t₁,t₂ ) dt₁dt₂. Очевидно, что

∞   ∞ x1 x2

q1q

C = sup                r(t1,t2) dt1dt2 I шДхД dx1 I w2(x2) dx2, где супремум берется по всем измеримым положительным функциям r таким, что

∞  ∞ p1

/ ( / (r(xi,X2))^{P 1} V1 (xi) dxi ) V2(x2) dx2 = 1.

Предположим обратное. Пусть C > MiM2. Тогда существуют числа p1 > 0 и р2 > 0 такие, что CC > pi >  Mi, i = 1, 2. Так как Mi < то, то в силу пункта b) леммы 1 задача. (1)—(2) имеет решение. Поэтому в силу теоремы 2 получим, что неравенство (5) спра-11

ведлнво с постоянной p^ ¹ pq ² для каждой абсолютно непрерывной функции u ( x₁,x₂). удовлетворяющей условиям (4). Отсюда следует, что C не является наименьшей постоянной в неравенстве (14). Полученное противоречие доказывает теорему 3. B

Следствие 1. Пусть выполняется все условия теоремы 2. Тогда по определению чисел Mi (i = 1, 2)

0                                                    ^t p ⁰

C 6 — sup--------1------------- Zwi(s)(gi(s))qi+1 ds, qi t>0 9i(t) - J(vi(s))1-pi ds 0

где gi(t) положительные измерил ше функции такие. что gi(t) >  J (v i (s)) ¹ pi ds.

Следствие 2. Пусть

Тогда.

и

C

∞

Bi = sup / wi(s) ds xi>0

x i

JvH (s)) ^{1 -} pi ds

p ⁰ p _i

i = 1,2.

2                q _i

B1B2 6 с 6 M1 M2 6 П (q i (q i ) ^pi ) B1B2

i =1

2                q _i

M1 M2 6П (q i (q i ) pi) с.

i =1

s(X1,X2) = <

2       ξ i

П   J[vi(ti)]1-pi dti i=1   0

i [v i⁽ x i⁾ ] ^{1 -p i} ,

0 ,

^(x 1 ^,x 2) G Pi ^2 ;

⁽ x1 ,x2) / P^i § 2 ,

где P^2 = { (x_i,x₂) G (0, то )² : 0 < x_i< ф, 0 < x₂ < £2 } 11 (ф ,£2) некоторая фиксированная точка в (0, то )². Очевидно, что

∞∞ j ( J(s(xi, X2))p1 Vi(xi) dxi

p ₂

p ₁

V2 (Х2) dX2

00 ξi

ξ 2     ξ 1     ₂

= /(/ П( /[v . (t . )] i =1

1- p ⁰ _{i dt i}

i [v i (x i )]1^-p i

p                 p 2

¹                       p ₁

v_i(x_i) dx_i    v₂(x₂ ) dx₂ = 1.

Поэтому функция s удовлетворяет равенству (16). Тогда из равенства (15) получим

∞ ∞ x1 x2

q1

C >                  s(t_i,t₂) dt_idt₂ I wi(xi) dxi I w₂(x₂) dx₂

∞   ∞ x1 x2

q1

>    \     \     / s(ti’t²) dtidt2 ) Wi(xi) dxi I W2(x2) dx2

ξ 2 ξ 1      0 0

∞   ∞ ξ 1 ξ 2 ₂ ξi

= / ( J (/ ^Z П (/[V i i )]^i- P 0 dy)

q p1i                  0               q1                      q21

[vi (t i )]^1-p i dtidt2 I Wi(xi)dxi ) Ш2(Х2) dx2

ξiq

= П ( / [v i (y i )]^i-p i dyi ) ^Pl / ^ i (x i ) dxi .

i=1 0

Переходя к супремуму в последнем неравенстве (относительно переменных ^i и ^2), по лучаем. что C > B_iB2. Неравенство C 6 M_iM₂ ввгтекает из теоремв! 3.

q _i

Теперь докажем, что Mi 6 q_i(q^,0 ) pi Bi, i = 1, 2. Прежде всего из определения величин

Bi вытекает, что

∞ p ⁰ _i

^B i ^qi

q _i

x i

> Кл. )]^i-p i dti.

Положив в равенствах (8)

p0   ∞ gi (x.) = qi Biqi ^j w.

p _i

⁽y i ) у.)   qi ,

i = 1, 2,

xi

находим, что

Mi = p i inf sup

6 sup

xi> 0

Поэтому

q i

xi

xi> 0

pi ∞ qiBii ( J ^i(ti) dti)

x i

p ⁰ i

^^^^^^^^г

xi

J [v i (t i )]¹ pi dti

∞

х

p _i

J ^i(ti) qiBB^i^J

Wi(yi) dyi

p0i

qi +1

p ⁰ p _i

dt i

ti

(q i )

^qi +1 p ⁰ p _i

B

1+ p0i

xi

∞

pi ∞ qiBiqi (J wi(ti) dti)

x i

p ⁰ p _i

^^^^^^^^r

xi

J [vi(ti )]1 pi dti 0

j dtiK^ ' ■ y dy i)

ti

p ⁰ _i

qi0 +1  1+pi

6 (qi) pi B qi sup xi>0

Bi

∞

∞

J Wi(ti) dti xi p0i   ∞              - p0i     xi qiBiq ( J ^i(ti) dti) qi - J[vi(ti)]1-pi dti xi                          0

JwM dyi

∞

pi

6 B^qi

xi

.

pi qiBiq ( / Ui(ti) dti

xi

) qi - /[V i (t i )]1^-p0 dt i >  (q i -

∞ p ⁰ _i

1)B iqi ( J

xi

p ⁰ _i

Wi(ti ) dt i

qi

Таким образом,

0 pqi0i +1 1+qi              qi i = 1,2.

Mi 6 —-----i— = qi(qi) pi Bi, pi

(qi - W

А это означает, что неравенство (17) доказано. Неравенство (18) автоматически следует из неравенства. (17). В

Замечание 2. Из следствия 2 вытекает, что для справедливости неравенства. (14), необходимо и достаточно, чтобы Bi < +то, i = 1, 2. В одномерном случае неравенство типа. Харди подробно изучено в монографии [10] (см. также [5]).

Следствие 3. Пусть выполняются все условия теоремы 1. Предположим, что р1 = Р2 = Р и q1 = q₂ = q. Тогда теорема 1 справедлива в обычном весовом пространстве Лебега, с весами v(x1 ,x₂ ) = v1 (x1)v₂(x₂) ii w(x1,x₂ ) = w1(x1 )w₂(x₂).

C Достаточность непосредственно следует из теоремы 2. Докажем необходимость. Пусть выполняется неравенство (3) для каждой абсолютно непрерывной функции u(x1 ,x₂ )• удовлетворяютней условию (4). Тогда, C 6 Co < то, где C — постоянная в ра венстве (15). Из неравенства (17) следует, что Mi < то, i = 1, 2. Тогда в силу пункта b) леммы 1 задача (1)-(2) имеет решение для каждого Ai >  Mi, i = 1, 2. В

• _а. , _х pqi (pi -1- ^ai) ^— 1

ПРИМЕР. Пусть 1 < pi 6 qi < то, v_i(x i ) = x^, w_i(xi ) = x i i , i = 1, 2. Тогда для справедливости неравенства (14), необходимо и достаточно, чтобы ai < pi — 1, i = 1, 2.

Аналогичным путем можно показать, что теорема 1 имеет место для пространства Лебега со смешанной нормой и с переменным показателем суммируемости. А именно, имеет место следующая

Теорема 4. Пусть 1 < р1 6 q1(x) 6 q1 < то и 1 < р₂ 6 q₂(x₂) 6 q₂< то. Предположим. что vi 11 wi — весовые фупкпшв определенные па (0, то), п дл^ i всех t £ (0, то) существует производная w'(t). Тогда следующие утверждения эквивалентны:

• а)    существует положительное решение следующей системы с локально абсолютно непрерывным производным первого порядка, уравнения

  /|У У /p II l , ₁₍„„ )( . i >t) — Aiwi(i)(y'₁(t))^1/pl = 0, )»V2 y2 /p ² «L„,x₃,( x ₃ >t ) - A2 W2(t)(y2 (t))^V p ² =0,

yi(t) > 0, y i (t) > 0, yi £ AC (0, то), A i > 0;

• b)    имеет место весовая оценка

  d²u dx1 dx₂

  
  

  Р 1 ,Ш 1 Р2,Ш2

  
  

llullq i ,v i ,x i II           6 C0

q2,V2 X2

где u £ AC (R+₊),

I u(0, X2) = lim x i ^₊o u(x1, X2) = 0,

[u(x1,0) = lim ^ ₂^+o u(x1,x2) = 0.

Co > 0 — постоянная, не зависящая от u, и R++ = (0, то) х (0, то).