Исследование отражения плоской электромагнитной волны от планарной оптически активной структуры

В настоящее время значительный интерес представляет разработка современных метаматериалов [1-4], то есть композиционных структур, получающихся искусственным внедрением элементов в однородные среды (контейнеры). Изменение структуры осуществляется на уровне атомов (метаматериалы для оптического диапазона) или на уровне макроструктуры (СВЧ-метаматериалы). Благодаря преобразованиям микро- или макроструктуры, у искусственного метаматериала изменяются его электрофизические свойства (эффективные диэлектрическая и магнитная проницаемости) и, как следствие, проявляются электромагнитные свойства, которые не присущи естественным материалам природного происхождения. Самыми широко известными свойствами метаматериалов являются возможность создания на их основе суперлинз, невидимых и малоотражающих покрытий и др. Во время явления, когда в структуру метаматериала проникают элементы зеркально асимметричной формы, метаматериал принято называть киральным (хиральным). Свойства киральных сред СВЧ диапазона исследованы к настоящему времени очень подробно [5-8]. Основными свойствами распространения электромагнитных волн в киральном метаматериале являются: распространение волн с право (ПКП) и левокруговыми (ЛКП) поляризациями с различными фазовыми скоростями, а также кросс-поляризация падающего излучения. В настоящее время описаны исследования неоднородных киральных метаматериалов, а также излучения электромагнитных волн полосковыми антеннами, расположенными на подложках из метаматериалов.

Такое явление как киральность в оптическом диапазоне известно давно и связано с кристаллами. В данной работе проводится аналогия между естественными и искусственными киральными средами, кроме того, рассматриваются вопросы связанные с возможностью концентрации оптической энергии оптически активными кристаллами.

Материальные уравнения для оптически активной среды

Для начала докажем, что имеется возможность свести тензорные материальные уравнения для оптически активного кристалла к скалярным материальным уравнениям для искусственной киральной среды диапазона сверхвысоких частот [1-4]. Для достижения этой цели выведем формулы, которые связывают относительный параметр киральности для искусственной среды и параметр оптической активности для оптически активного кристалла.

Кристалл, подобно бигиротропной среде, можно описать с помощью материальных уравнений:

-►           -► -►           -►

D = е Е , В = ц Н ,             (1)

где е - тензор диэлектрической проницаемости; ц - тензор магнитной проницаемости.

В статье применяется общепринятая смешанная система единиц.

Тензоры е и ц , приведенные к главным оптическим осям кристалла, имеют следующий вид:

	s	0	- i X i "
-^- s =	0 _ i X i ■ц	s 0 0	0 s - i X 2 "	, (2)
-^- ц =	0 _ i X 2	ц 0	0 ц ,	’

Выражая из соотношений (6) x - и y - составляющие векторов поля оптической волны через продольные компоненты E_z и H_z , получаем։

^H x = T" E + i ~ H z ' k ₀ ц д y    ц

где X _i и X 2 - неопределенные безразмерные параметры.

Подставим тензоры (2) в материальные уравнения (1), в результате чего получим:

H ₌ _ i д E z y 7 Д ’ k 0 ц д x

= --i- °Hz + iXi E k0s дy     s

	" s 0 - i X i "
—-		——
D =	0 s 0	Е ,
	_ i X i 0 s _
		(3)
	ц 0 - i X 2
——		——
В =	0 ц 0	Н .
	_ i X , 0 ц _

. _ i дH z y                    "

k ₀ s д x

Подставляя соотношения (7) в третье и шестое уравнения системы (6), получаем следующие связанные дифференциальные уравнения второго порядка։

V i H z + k 0 ² 8Ц--Х 2 H z ц J

-

Уравнения Максвелла для оптически активной среды с учетом материальных уравнений (1) записываются следующим образом։

* *

rot Н = ik . Е (4) rot Е = - ik ₀ ц Н .

Пусть размер оптически активного кристалла вдоль оси Oz много больше его размеров вдоль других координатных осей:

^{- k} 0

s

X i +-X 2 ц

J>= ⁰

^V i E z + ^k 02 ^8Ц-Ц^Х 2 E z ⁺ s

, ц    д H

+ k0 X2 +-Xi      = 0, s Joy

дH.

d z » d x , d z » d y ,

где d_x ‒ размер кристалла вдоль оси Ox ; d_y ‒ размер кристалла вдоль оси Oy ; d_z ‒ размер кристалла вдоль оси Oz .

При выполнении условий (5) можно считать, что 5 / д _z = 0, что соответствует отсутствию за-

д д

где V, =—т + —т - оператор Лапласа по попе-i дx2 дy y речным координатам.

Считая, что зависимость векторов поля оптической волны от координаты y имеет следующий вид:

E z ( y ) , H z ( y ) ~ Ae ^{k 0} ^y ,          (9)

получаем следующие дифференциальные урав-нения։

висимости векторов поля от координаты z .

Спроецируем уравнения Максвелла (4) на оси декартовой системы:

v i H z + k 0 ² 8ц--х 2 H z ц J

-

дE     . „ .   „

—- = ^{- ik} o Ц ^H x ^{- k} 0 X 2 H z , д y

-^ Ez- = — ^ik 0 ^ H y , д x

дEy  дE   ,

• —     = ^k 0 X 2 ^H x ^{- ik} o Ц ^H z ,

д x   д y

H = ik0sEx + k0X1 Ez, дy дH

• ^- ^ = ^ik 0 ^{s E} y , д x

д H„ д H

—---- = - k _ox, E, + ik ₀ s E, .

01 x0 z дx   дy

- k ₀ ² д/ёц

s

X i +-X , ^ц

E z = 0,

^V i E z + ^k 02 ^ёц--Х 12 E z s

- k 02 д/ец

ц

X 2 +-X 1 s

-

H_z = 0.

Соотношения (10) ‒ связанные дифференциальные уравнения второго порядка оптически активного кристалла, рассматриваемого относительно продольных составляющих векторов поля световой.

Аналогичные уравнения для искусственной киральной среды имеют вид [9]։

VREz + k02 (еЦ + Х2)Ez -2ik°2ЦХHz = °, VRHz + k°2 (ец + X2)Hz + 2ik°2ехEz = 0.

Заметим, что в формулах (11) х -относительный параметр киральности для искусственной киральной среды.

Сравнивая систему дифференциальных уравнений для оптически активной среды (10) и для искусственной киральной среды (11) можно сделать вывод о том, что они имеют полностью аналогичный вид.

После установки сходств и различий уравнений (10) и (11) легко получить формулы связи между относительными параметрами кирально-сти и оптической активности.

Таким образом, доказано, что при выполнении условий перехода от параметра киральности к параметру оптической активности:

х=i!;x

X2 = i материальные уравнения ной среды

для оптически актив-

-i X1"

2 Е ,

е

Jn              (13)

— i X 2

2 Н

Ц являются полностью эквивалентными соотноше- ниям для искусственной киральной среды:

—— ——         ——

D = еЕ - ixH,

——        ——         ——

В = ц Н + i х Е .

Для оптически активных кристаллов х ₂ = ° и ц = 1, следовательно, формула перехода принимает с учетом (14) следующий вид:

УА

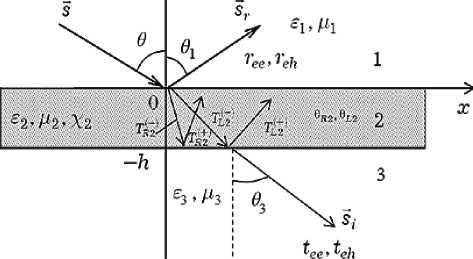
Рисунок 1. Геометрия оптически активной планарной среды

Х = - i^Х^- (15)

V е

В итоге, для перехода от решения задач с ки-ральными метаматериалами СВЧ к решению задач с кристаллами необходимо в конечных соотношениях заменить (15) и применить новые дисперсионные зависимости материальных параметров е и х 1 , справедливые для оптического диапазона.

Отражающая планарная оптически активная среда

Приведем пример, когда линейно поляризованная электромагнитная волна (ЭМВ) отражается от оптически активного планарного кристалла, геометрия которого представлена ниже.

Из рисунка 1 можно выделить три области: 1 ‒ диэлектрик, 2 ‒ оптически активный кристалл и 3 ‒ диэлектрик.

Они обладают параметрами е 1 , ц 1 - относительные диэлектрическая и магнитная проницаемости первой области; 0 = 0 1 - углы падения и отражения ЭМВ от границы раздела «диэлектрик 1 - оптически активный кристалл»; е ₂, ц ₂, х 2 - относительные диэлектрическая, магнитная проницаемость и параметр оптической активности области 2; 0 R ₂, 0 L ₂ - углы преломления волн ПКП и ЛКП в область 2; е ₃, ц ₃ - относительные диэлектрическая и магнитная проницаемости третьей области; 0 3 - угол прохождения ЭМВ из оптически активного кристалла в область 3; r_ee , r_eh ‒ коэффициенты отражения для основной и кросс-поляризованной компоненты электромагнитного поля (ЭМП) в области 1; T R - , T LL - ) - коэффициенты прохождения для волн ПКП и ЛКП; T R ⁺ , Т + - коэффициенты отражения от границы раздела «оптически активный кристалл ‒ область3» для волн ПКП и ЛКП; t_ee , t_eh ‒ коэффициенты прохождения для основной и кросс-поляризованной компоненты ЭМП в области 3.

В оптически активном кристалле электромагнитное поле представляется в виде суперпозиции четырех волн с круговыми поляризациями ‒ двух прошедших в оптически активный кристалл из диэлектрика (области 1) с коэффициентами прохождения T R ^-^ и Т^ и двух отраженных от границы раздела «оптически активный кристалл ‒ область 3» обратно в область 2 с коэффициентами T R^ и Т^ Индексы «R» относятся к волнам ПКП, индексы «L» ‒ к волнам ЛКП.

Для определения продольных составляющих векторов ЭМП в оптически активном кристалле воспользуемся известными соотношениями [9]:

E _ t e~ik R ^{( s} R ’ ^r ) + t e i^k R ^{( s} R ’ ^r ) +

+ t ^{( — )} e ~ ^iki ⁽ s i ’ r ) + T (⁺) e k ⁽ s i ’ r ) ■

H _ i Г t** e~^ik R ^{( s} R ’ r ) + t¹¹ e i^k R ^{( s} R ’ r ) +     ⁽¹⁶⁾

^Z V R        R

E? = i ( cos 6 R [ T Rf² e ⁽ x ^{sin 6 R - y cos 6 R} )

— T (⁺V>( x sin 6 R — y cos 6 R

^T R e

^^^^^^в

^^^^^^в

^^^^^^^

+ T^² e "  ‘k ^{1 (} s ¹ ’ r ) + tL^ e k

cos 6 _L [ T L"² e ⁽ x ^{sm 6} 1 ^— y ^{cos 6} 1 ) _— T ( ⁺ ) e ( x ^{sin 6} 1 ^— y ^{cos 6} 1 ) ! ) "

^^^^^^в

где sR. 1, = { sin 6 _{R L}, — cos 6 _{R L} } - единичные вектора, вдоль которых распространяются преломленные

волны; _s R⁺L = { sin 6 _{R L} ,cos 6 _{R L} } - единичные вектора, вдоль которых распространяются прошед

-

-

^шие волны; ⁶ R , L ^- углы преломления волн ПКП

и ЛКП, соответственно; n^{( 2 )} =

‒ импеданс

(характеристическое сопротивление) оптически

I    X активного кристалла; kRL = k01 n2 + i -A2=-’ I       Vs

по‑

стоянные распространения нормальных волн ПКП и ЛКП в оптически активном кристалле; n 2 = {s₂ - относительный показатель преломления области 2.

Распишем выражения для продольных состав‑ ляющих в более подробном виде։

E^ =

_ rp ( ^— ) ^{— ik}R ( x sin ⁶ R ^— У ^{cos 6} R )

_ 1R e              +

+ T ( ⁺ ) e^{llk R} ( x ^{sin 6} R ⁺ у ^{cos 6} R ) +

+ t ( — ) e — ik i ( x sin 6 1 — у cos 6 1 ) +

( ⁺ ) ^^ki ( x ^{sin 6} 1 ⁺ у ^{cos 6} 1 ).

^{+ T} i ^e                ;

h Z ²⁾ =

_ i ( T ( ^— ) e^{- ik} R ( x ^{sin 6} R ^— у ^{cos 6} R ) +

( ⁺ ) „^ik R ( x ^{sin 6} R ⁺ у ^{cos 6} R ) _

^{+ t}r e

( — ) — ik i ( x sin 6 1 — y cos 6 1 )

— Ti e              —

_— T ( + ) e ik i ( x sin 6 1 + У cos 6 1 ) )

Выражения для составляющих ЭМП

E^ и

If¹’ в оптически активном кристалле имеют вид:

Е2^

в

H^2 = -

k 0 ^s 2 I X

^S 2

к Is ₊X 1 tv 0 ^s 2 +

^S 2

x2 de?2 + . ,7/

14 d У    d y

.   5E{2)—i e7 ——2  5y

в

;

(2.3)

x 2 d hZ²⁾"

S 2 5 y

.

Подставляя выражения (17) в соотношения (18), получаем։

H X ²⁾ = Vs ? ( cos 6 _R [— 7 X e⁽ x sin^{6 R - y cos 6 R} ) + + T (⁺) e ( x ^{sin 6} R ^- у ^{cos 6} R ) { _—

в

cos 6 _L Г T²"²e ⁽ x ^{sin 6 1 — y cos 6 1} ) _— T ( ⁺ ) e ( x ^{sin 6} 1 ^— у ^{cos 6} 1 ) ! )

в

Для определения углов преломления волн

ПКП и ЛКП 6 R _L воспользуемся законами Снел-лиуса [9]:

sin 6 3 = ^k R , 1 . sin ⁶ R , 1 ^k 3 ’

sin 6, = sin 6

3 R , L

S' + i

N ^S 2

n ₃

.

Τаким образом, выражения для составляющих

электромагнитного поля в оптически кристалле имеют вид:

p ( ²) _ тЧсГi^k R ( x ^{sin 6} R ^— y ^{cos 6} R ) _i_

Ez =TR e

+ T ( ⁺ ) e ik R ( x ^{sin 6} R ⁺ у ^{cos 6} R ) +

+ t ( — ) e — ^lk i ( x sin 6 1 — у cos 6 1 ) +

( ⁺ ) „ik i ( x ^{sin 6} 1 ⁺ у ^{cos 6} 1 ).

+ Ti e;

H (²) _ i ^S~ ( T ( ^— ) e^{- lk} R ( x ^{sin 6} R ^— у ^{cos 6} R )

+ T ( ⁺ ) e ik R ( x ^{sin 6} R ⁺ у ^{cos 6} R ) _—

( — ) „— lk i ( x sin 6 1 — y cos 6 1 )

— T1 e

— T (+) eiki (x sin 61 + У cos 61)) • e{2)= i (cos 6 R Г TRf2 e(xsin 6 R—y cos 6 R)

_ T ( + ),,( x sin 6 r — y cos 6 r

^T R e

в

активном

+

в

в

cos 6 _L [ TL^e ⁽ x ^{sm 6} l ^{— y cos 6} l )

Т ( + ) „( x sin 6 1 — y cos 6 1 )

^{— T} 1 ^e

;

в

H X ²⁾ = 4ч ( cos 6 _R [— T Rf² e² x ^{sin 6 R —} y ^{cos 6 R} ) + + T (⁺) e ( x ^{sin 6} R ^— у ^{cos 6} R ⁾] _—

в

cos 6 _L Г T L"² e ⁽ x ^{sin 6 1 —} y ^{cos 6 1} ) _— T ( ⁺ ) e ( x ^{sin 6} 1 ^— у ^{cos 6} 1 ) ! )

в

где

sin — sin 0

n ₁

J_ » R ₽ R ⁽ h ).

( 2 ) e

n(

i _p -i^k R P R ( h ).

( 2 ) e            ’

n(

^S 2

cos 0_R, — 1 -

R , L

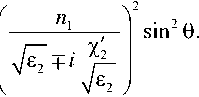
^l_p-)L P L ⁽ h )                  i_ - i ^ik L P L ⁽ h )

^5         ( 2 ) e ;    ^6        ( 2 ) ^e

n               n

A88 eik-ikзвз(h), где

В результате при использовании граничных условий получаемм систему линейных алгебраических уравнений относительно неизвестных коэффициентов отражения и прохождения для оптически активной среды:

cos 0 ₃ —

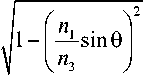
ee

eh

T (+)

TR

^

A

T(-)

TR

T (+)

TL

T(-)

TL tee teh

- 1 cos 0 1 n^{( 1 )} 0

C

R , L

— cos0„ , — R , L

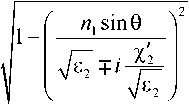
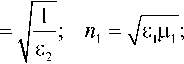
p i ( h ) — h cos 0 i ; n ₂ — ^/s ^ .

A 11 = A 17 = A 18 = A 22 = A 27 = A 28 = A 32 = ^— A 37 ^— A 38 ^— A 41 ^— A 47 ^— A 48 ^— A 51 =

Система (21) определяет требуемое решение задачи и из нее определяются коэффициенты отражения и прохождения.

Дисперсионный анализ оптически активной среды

— A 52 — A 57 — A 61 — A 62 — A 68 — A 71 —

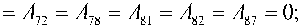
А = А = А — А — А — А = — Ь

21      42      ;      23      24      25      26         ;

A ₁₂ — n^{( 1 )} cos 0 ; A ₁₃ — - A ₁₄ — iC R ;

A 15 ^— A 16 ^{— iC} L ; A 31 ^—

cos 0

n(1)

R

33      ^л34          ( 2 ) ;

n(

L

35      ^Л36          ( 2 ) ;

n⁽ )

А = А =

43      44

-

i

( 2 ) ^;

П( )

i

А = А =----

45    ^л46       ( 2 ) ;

П( )

A ₅₃ — - iC R e ^{k R e} R ⁽ h ) ; A 5 ₄ — iC R e - i^k R ^e R ⁽ h ) ;

A 55 — iC_Le ^k L ^{e L (} h ) ; A 5 ₆ — - iC_Le - k ^{e L (} h ) ;

A 57 — -n^{( 3 )} cos 0 3 e i ^{зРз (} h ) ; A 6 ₃ — e ^ik R ^e R ⁽ h ) ;

- ^ik R P R ⁽ h )                   ^ik L P L ⁽ h )                   - ^ik L P L ⁽ h ).

64 ^— e ;      65 ^{— e} ;      66 ^{— e} ;

- i^k 3 ^₽ 3               C R__p- ^k R ^e R ⁽ h ).

67 ^e ;    ^73       ( 2 ) ^e ;

n⁽ )

A 74 —	_ _C R_ р- ik R Р R ( h). ( 2 ) e            ’ n( )	C^pik L P L ( h ). 7175        ( 2 ) e         ; n( )
А 76 — -	. Ck p -ikL P L ( h ). n( 2 ) e         ;	_ cos 0 3    ik з Р з ( h ) A 77 — n ( 3 )   e

При проведении дисперсионного анализа важно принимать во внимание дисперсию вещественных параметров оптически активной среды, аименнозависимость е ( ю ) и % ( ю ) .

Для модели оптически активной среды дисперсия диэлектрической проницаемости определяется следующим законом:

^еИ — ¹ + _^в’ - (22)

Q0 - ю где р0 - удельное вращение; Q0 - резонансная частота поглощения кристалла.

Заметим, что параметр оптической активности также зависит от частоты: X —х ( ю ) . В научной литературе [10] указывается, что для оптически активной среды частотная зависимость параметра оптической активности определяется следующим образом:

X ( ™ ) ⁼ A 0 -775°^ - (23) c ( Q ₀ - ю )

где A ₀ ‒ расстояние между соседними атомами в кристаллической решетке, c ‒ скорость света. Резонансные частоты Q ₀ и удельное вращение р ₀ для различных кристаллов ‒ разные.

Формулы для частотных зависимостей постоянных распространения волн ПКП и ЛКП в безграничной оптически активной среде имеют вид: kR,L (®) = k0 [7ё(ю) ± х(ю)] = k0

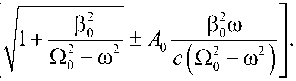
Оценка полученных результатов

Для решения поставленной задачи в первую очередь необходимо определить корреляцию между r_ее , t_ее основной компоненты световой волны и X , 0 .

При решении задачи будем считать, что на рассматриваемую структуру падает плоская электромагнитная волна перпендикулярной поляризации под углом 0 = 0 и что области 1 и 3 представляют собой вакуум, то есть обладают параметрами s 1 ₃ = Ц 1 ₃ = 1.

При численном расчете отражательных характеристик оптически активных кристаллов были использованы значения параметров приведенные в таблице. Прослойка оптически активного кристалла в каждом примере составляет 1 и 1 5 мм.

Таблица 1. Параметры оптически активных кристаллов

№	Название формула	Показатель преломления	Параметр оптической активности
1	SrS 4 О 6 (дитионат стронция)	2 34	3,4 - 10 - 3
2	СаЅ4О6 (дитионат кальция)	2 17	2,27 - IO - 3
3	СаСО3 (исландский шпат)	1 65	1,4 - 10 - 2

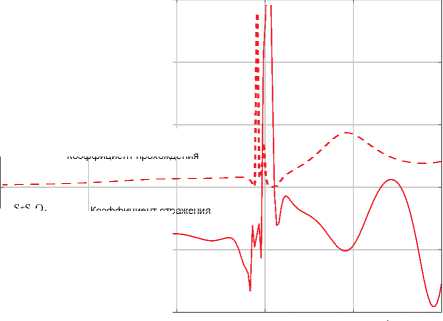
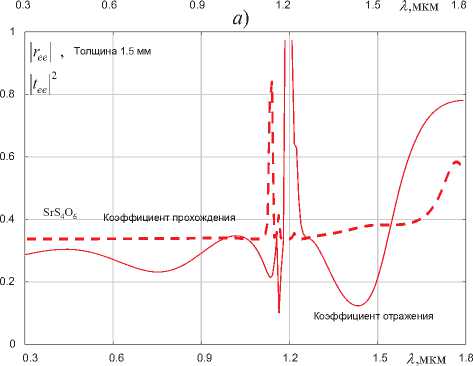
На рисунке 2 приведены зависимости квадратов модулей коэффициентов отражения и прохождения основной компоненты поля при нормальном падении волны с перпендикулярной поляризацией на дитионат стронция. На рисунке 2 а прослойка оптически активного кристалла ‒ 1 мм (аналогично для рисунков 3 а и 4 а ) на рисунке 2 б ‒ 1 5 мм (аналогично для рисунков 3 б и 4 б ).

Толщина 1 мм

0.6

0.4

0.2

0.8

Коэффициент прохождения

SrS4O6

Коэффициент отражения

б )

Рисунок 2. Зависимости квадратов модулей коэффициентов отражения и прохождения основной компоненты поля от длины волны при нормальном падении волны с перпендикулярной поляризацией на дитионат стронция

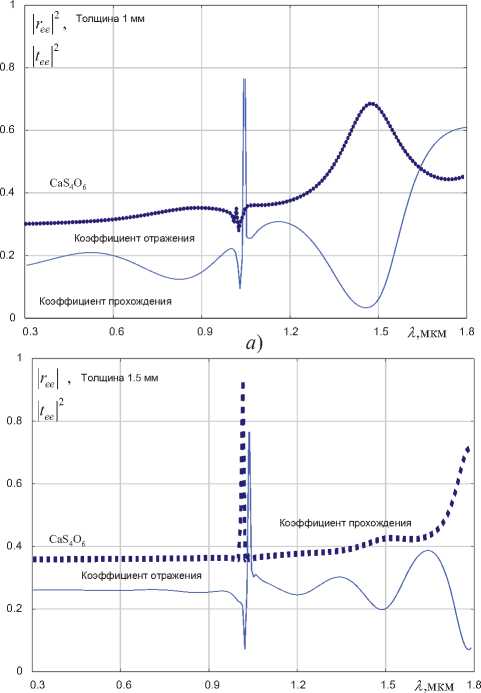
б )

Рисунок 3. Зависимости квадратов модулей коэффициентов отражения и прохождения основной компоненты поля от длины волны при нормальном падении волны с перпендикулярной поляризацией на дитионат кальция

На рисунке 3 представлены зависимости квадратов модулей коэффициентов отражения и прохождения основной компоненты поля при нормальном падении волны с перпендикулярной поляризацией на дитионат кальция.

На рисунке 4 приведены зависимости квадратов модулей коэффициентов отражения и прохождения основной компоненты поля при нормальном падении волны с перпендикулярной поляризацией на исландский шпат. Расчеты во всех трех представленных выше случаях были проведены на следующих длинах волн։ от 0,3 до 1,8 мкм.

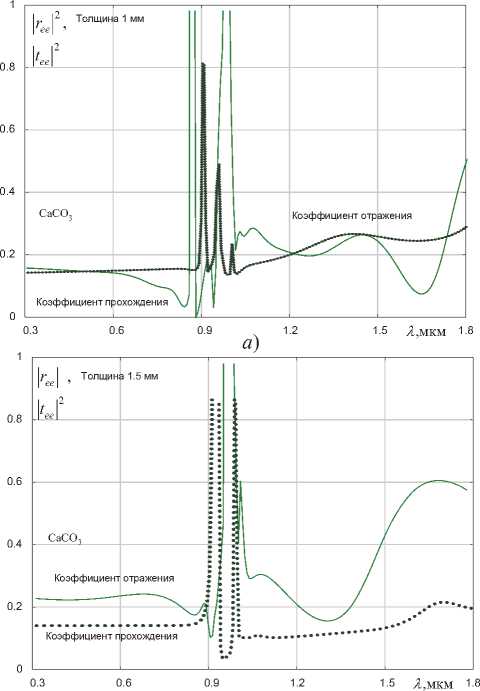
б )

Рисунок 4. Зависимости квадратов модулей коэффициентов отражения и прохождения основной компоненты поля от длины волны при нормальном падении волны с перпендикулярной поляризацией на исландский шпат

Выводы

• 1.    В оптически активных кристаллах на некоторых частотах имеется возможность преобразовать нормально падающее оптическое излучение в азимутальное рассеяние. Этим свойством обладают как искусственные метаматериалы СВЧ,

• 2.    Проведя оценку полученных результатов, можно говорить о том, что исландский шпат будет характеризоваться оптимальными концентрирующими параметрами и максимальным значением аргумента оптической активности, что обусловлено прямой пропорцией удельного вращения кирального активного кристалла к уровню бокового рассеяния.

• 3.    Ввиду того, что параметр оптической активности в 100 раз меньше относительной характеристики киральности метаматериала в СВЧ диапазоне показатель изменения нормально падающего оптического излучения в поверхностное рассеяние метаматериала разительно отличается в меньшую сторону от аналогичной характеристики искусственного метаматериала.

так и естественные кристаллы в оптическом диапазоне.