Исследование параметрических резонансных колебаний в ходовой части гусеничной машины

Введение. Повышение подвижности транспортных средств является актуальной проблемой. Для ее решения в современных машинах увеличивается мощность двигателя, совершенствуются свойства трансмиссии, движителя, систем подрессоривания и управления движением. Однако реализация потенциальных скоростных свойств быстроходных гусеничных машин ограничивается рядом не исследованных ранее динамических явлений, возникающих при взаимодействии гусеничного движителя с опорной поверхностью (Янчик и др. 2005 [1], Вонг, 1995 [2]) и приводящих, в частности к ограничению долговечности элементов конструкции движителя вследствие высоких динамических и температурных перегрузок, потере устойчивости движения машины и т. д. Движение гусеничных машин осуществляется в основном вне дорог, на неподготовленных природных территориях, начиная от пустынного песка, заболоченной местности и заканчивая снегом (Вонг, 1995 [2]). Однако при движении по твердой поверхности - мерзлый грунт,, бетонные трассы и др. - возникают динамические явления, существенно ограничивающие ресурс элементов движителя.

Проблема взаимодействия движителя гусеничных машин с рельефом местности всегда привлекала значительное внимание исследователей. Новаторские работы были основаны прежде всего на эмпирическом подходе к предмету исследования. Первые публикации в этой области были сделаны Беккером (1969) [3], а затем Уилером (1977) [4], Вонгом (1984) [5] и другими учеными. Беккер является инициатором широких исследований системы «движитель – опорная поверхность», а Муро and O’Брайен в 2004 г.) [6] создали полуэмпирические модели взаимодействия движителя с местностью, которые являются основой террамеханики гусеничных транспортных средств. В своей работе они упростили процесс взаимодействие между движителем с опорной поверхностью, рассматривая опорный каток, как жесткую опору.

Вонг (2001) [7] описал более сложную модель, в которой гусеница предполагалась «гибкой». В работе Вик (1996) [8] гусеница также моделируется как гибкая и нерастяжимая нить. Данные математические модели позволяют описать взаимодействие гусеницы с опорным основанием.

Галастис (1961) [9] описал метод, который позволяет прогнозировать динамические нагрузки, возникающие в движителе быстроходных гусеничных машин. Ли и соавт. (1998) [10] описали взаимодействие между звеньями гусеницы и другими элементами движителя, такими как опорные катки. Они представили результаты компьютерного моделирования крупномасштабной гусеничной машины со ста шестнадцатью степенями свободы.

Уилер (1997) [11] представил компьютерную программу, которая позволяет имитировать динамику движения гусеничной машины. Современные разработки компьютерных методов и все более передовых технологий дают возможность проводить точное моделирование больших и сложных систем. В рамках данной концепции Маидр (2002, 2006) [12] представил модель взаимодействия « опорный каток – гусеница – опорное основание» на основе метода конечных элементов. Модель представляет собой сегмент гусеницы, который взаимодействует с опорной поверхностью и опорными катками при представлении гусеницы в виде непрерывной ленты с жесткими связями. В работе задействован так называемый силовой «суперэлемент», который включает в себя гусеничный сегмент, два опорных катка и грунт под гусеницей между опорными катками. Санду и Фриман (2005) [13] использовали метод моделирования «суперэлементов» для высокоскоростных военных гусеничных машин, предполагая, что гусеничная цепь может быть смоделирована как непрерывная гибкая нить. Таким образом, проведенный анализ показал, что известные модели описывают взаимодействие движителя с опорным основанием при движении, как правило, по деформируемому грунту, когда контакт первого опорного катка с сегментом гусеницы приводит к погружению траков гусеницы в грунт. Следующие опорные катки двигаются по относительно ровной поверхности гусеницы. В таких условиях жесткость неподрессоренных элементов конструкции гусеничного движителя не оказывает существенного влияния на характер динамического нагружения опорного катка и беговой дорожки гусеницы.

В тоже время при движении по жесткой опорной поверхности (скалистые горные дороги, обледенелые трассы) влияние звенчатости гусениц на динамические процессы становится существенным. Применение обрезиненных беговых дорожек и резино-металлических шарниров (РМШ) в конструкциях гусениц приводит к усложнению процесса формирования динамических высокочастотных нагрузок в ходовой части и усложнению математических моделей, вследствие возникновения не учитываемых ранее явлений, например отрыва катков от беговой дорожки [1, 14– 15]. В результате повышенного вибрационного нагружения выходят из строя не только элементы конструкции гусеничного движителя и системы подрессоривания, но и различное оборудование, устанавливаемое на базовом шасси. Несмотря на то, что в отечественной литературе, в отраслевых стандартах гусеничная цепь тоже, как правило, рассматривается в виде деформируемой однородной ленты, Аврамов В.П. [16] в своих работах обратил внимание на существенное влияние звенчатости гусениц на уровень динамической и тепловой напряженности опорных катков. При этом в отдельных работах указывается, что характер взаимодействия опорного катка с беговой дорожкой гусеницы носит нелинейный характер, что может привести к параметрическим резонансным колебаниям [17].

Таким образом, целью предлагаемого исследования является снижение динамической и тепловой нагруженности опорных катков гусеничных машин при движении по твердым грунтам.

Для этого разрабатываются математические модели, выполняется их верификация, исследуются причины, приводящие к нарушению устойчивости периодических решений, обосновываются варианты технических решений, позволяющих достичь поставленную цель.

Разработка математических моделей и теоретическое исследование

Исходными данными при разработке математической модели являются параметры реального объекта исследований – быстроходной гусеничной машин массой 14 т. При этом параметры шины опорного катка и беговой дорожки гусеницы определяются используемыми материалами. Шины ОК изготовлены из резины марки 4Э-1386 (Е = 7,36 МПа), резиновый слой гусеницы изготовлен из материала 51-3064 (E = 7,36 МПа). Совместная жесткость упругого взаимодействия «шина–дорожка» определялась методом конечно-элементного моделирования и проверялась экспериментально. Схема экспериментального определения деформации шины и резинового слоя гусеницы объекта исследования приведена на рис. 1.

По результатам расчетно-экспериментального исследования на серийной машине установлено, что величина вертикальных перемещений опорного катка изменяется от 5,017 до 6,187 мм. При этом максимальные деформации наблюдаются при перекатывании катка через резинометаллические шарниры (РМШ). Минимальные деформации фиксируются при положении катка на середине плитцы трака.

Для оценки динамической и тепловой нагруженности используется двухмассовая математическая модель, учитывающая колебания неподрессоренной массы опорного катка, подрессоренной массы корпуса машины, а также включающая в себя блок расчета температуры массивной шины.

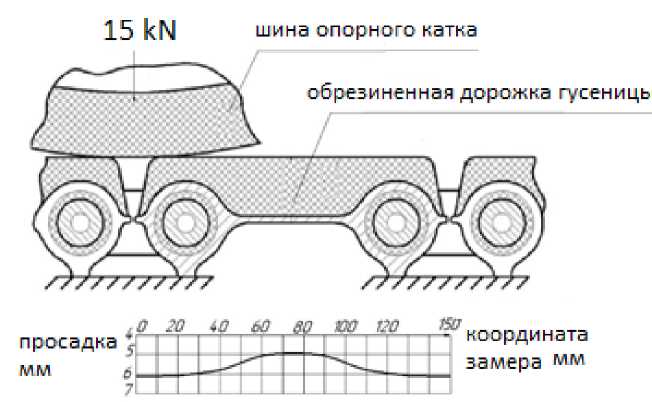
Рис. 1. Схема совместного экспериментального определения деформации шины и резинового слоя гусеницы объекта исследования

• - 1∗( 1- ∗ sin( ))- 2∗( 1- 2)- 1∗( 1^̇ - ∗ ^̇∗cos( ) _⎪^⎧ ̈1=                               _m1

• ⎪                       - 2∗( 2- 1)- 2∗( 1^̇ - 2^̇

  
  

=          m2

• A= / ^w=(    ^̈1∗ b )-     ^̈1∗ b )∗ V ∗ s ∗ℎ t _ cpct _ air

⎪A t=Tokr+, ⎩                                  ht_cpct_rubber где А – механическая работа, идущая на нагрев шины, Дж; Z̈ – ускорение опорного катка; V – скорость БГМ; S – площадь поверхности массивной шины; ht_cpcat_air – удельная теплоемкость резины; Тokr – температура окружающей среды; t – температура массивной шины.Значение параметров, необходимых для выполнения расчета, приведены в таблице.

Существующая в настоящее время методика расчета тепловой напряженности шин опорных катков разработана в сороковых годах прошлого века Козловым А.Г. и подробно изложена в работах [18]. Температура массивной шины определяется на основе расчетной схемы (рис. 2).

Таблица

Параметры расчета температуры массивной шины

Обозначение переменной	Наименование	Значение
C1	жесткость взаимодействия шины катка с гусеницей	3000000
C2	статическая торсиона	47000
m1	масса катка, кг	35
m2	масса машины, приходящаяся на один каток	1800
L	шаг гусеницы, м	0,15
w	траковая частота	2 ”v/l
a	деформация массивной шины, м	0,001
b	коэффициент диссипации в резине	1600
mss_tire	масса резины, нагреваемой в момент времени, кг	0,336
ht_cpct_rubber	удельная теплоемкость резины, J/kg*С	1420
init_tmprt	температура потоков воздуха, С	20
A_heatexchange	2 площадь поверхности охлаждения, м	0,002
ro_air	плотность, kg/m^3	1,2

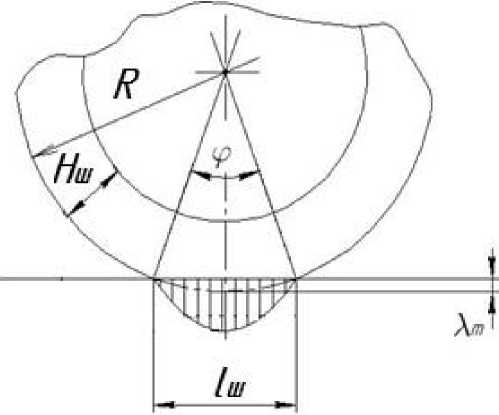
Рис. 2. Схема расчета резиновой шины опорного катка

Температура шины опорного катка определяется по зависимости:

т = в

+ _∝ ш ^,

где t в – температура окружающего воздуха, К ; Q – количество тепла, выделяемое в массивной шине за 1 с работы, Дж ; α – коэффициент теплоотдачи от резины к воздуху, Вт/(м^2.К) . Количество тепла Q определяется величиной диссипации энергии в процессе упругой деформации шины опорного катка и учитывается коэффициентом ψ внутреннего трения резины, ψ=0,25 …0,5 по формуле (4).

,       3.6nR, где n – частота вращения опорного катка, об/мин; V– скорость движения машины, км/ч; А – работа деформации массивной шины за один оборот опорного катка

А =        шк( 1-^) .                             (4)

Коэффициенты, входящие в данное выражение, рассчитываются следующим образом:

I2

Л_т = ^ш – максимальная деформация массивной шины, м; I_ш

– длина хорды, по

4Р которой происходит контакт шины и беговой дорожки гусеницы, м ; Чт =     – максимальное ш ш удельное давление в контакте шины с обрезиненной беговой дорожкой, Па.

Результаты моделирования по (1) показали, что максимальные высокочастотные виброускорения неподрессоренной массы при движении по твердому грунту достигают величины 30g. При этом температура внутренних слоев массивных шин достигает величины 150 …160 градусов при движении в резонансном режиме за время менее 60 секунд. При этом допустимая температура используемого клеевого материала составляет 153 градуса. Следствием этого является интенсивная деградация массивных шин опорных катков (рис. 3).

Рис. 3. Каток быстроходной гусеничной машины с расслоившейся массивной шиной опорного катка

Это подтверждается результатами ранее выполненных измерений температуры в массивных шинах опорных катков БГМ, приведенных на рис. 4.

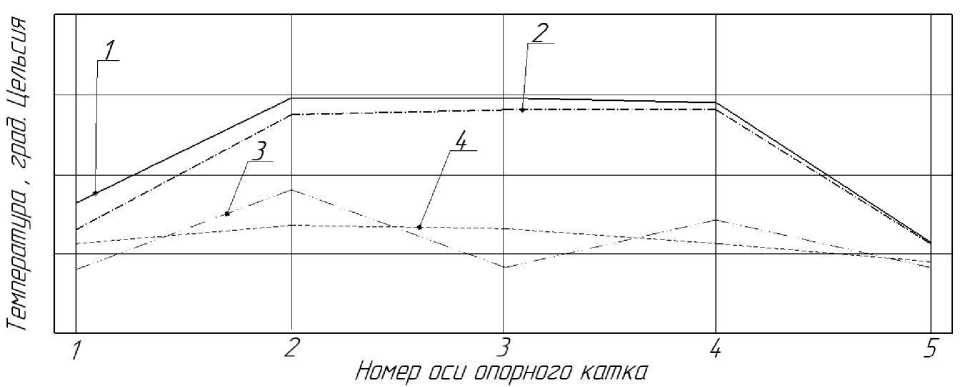
Рис. 4. Распределения температуры внутри массивных шин и на ее поверхности 1,2 – температура внутри массивных шин опорных катков правого и левого бортов; 3,4 – температура на поверхности массивных шин опорных катков правого и левого бортов

Как следует из рис. 4 температура в сердцевине массивных шин 2-го, 3-го, и 4-го опорных катков стабильно держится на уровне 150 градусов Цельсия, что свидетельствует о перегреве шин опорных катков в процессе эксплуатации.

Как указывалось выше, в существующих методиках расчета температура массивной шины определяется без учета звенчатости гусеничного обвода [18]. В то же время при воздействии на массивную шину постоянной статической нагрузкой, но при переменной жесткости в контакте массивной шины ОК и обрезиненной беговой дорожки, что учитывается в модели (1), удельное давление в контакте не является постоянным, а меняется в соответствии с «траковой» частотой, что приводит к периодическому изменению деформации массивной шины. Результатом этого является возникновение параметрических колебаний, с периодически изменяемым параметром c(t) - жесткостью [17].

Используемая в работе методология оценки устойчивости периодических решений при параметрических колебаниях подробно изложена многими авторами [19], а применительно к формированию нагрузок на опорный каток в работе [17]. В данном исследовании уточнены границы неустойчивости динамического процесса с учетом влияния диссипативных сил, определяемых экспериментально. На рис. 5 приведен анализ устойчивости системы без учета диссипации, а на рис. 6 с учетом диссипации.

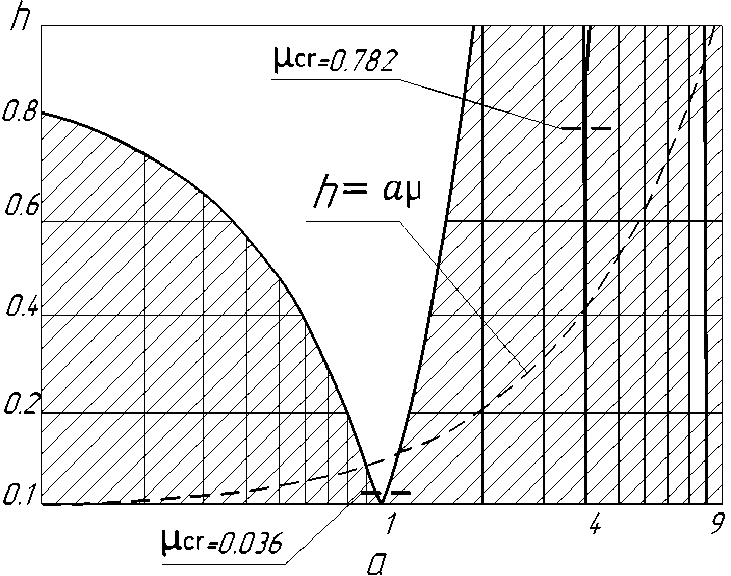
Рис. 5. Анализ устойчивости системы без учета диссипативных сил

Как следует из рис. 5 и 6, зоной резонанса является клиновая область на диаграмме Айнса-Стретта, соответствующая параметру а = (~“) = 1 (см. рис. 5) и коэффициенту расстройки ^ =2 (см. рис. 6). В обоих случаях центральная точка клина соответствует скорости 23,8 км/ч. Кроме того очевидно, что учет диссипативных сил незначительно расширяет область устойчивости. Тем не менее результаты, представленные на рис. 6, позволяют определить минимально необходимое значение параметра ^, при котором параметрический резонанс будет полностью исключен. Данное условие выполняется при значении и = 0,035. Применительно к объекту исследования параметрический резонанс возникает при скорости движения машины от 21,27 км/ч до 26,27 км/ч.

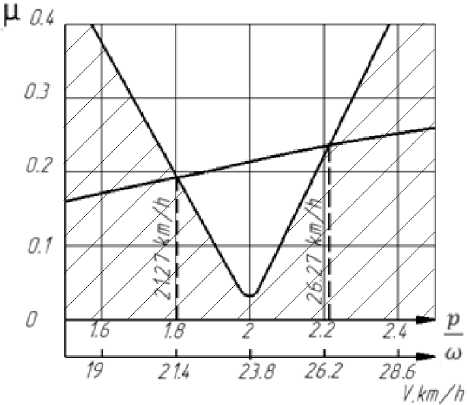
Рис. 6. Анализ устойчивости системы с учетом диссипативных сил

Результаты эксперементального исследования и численного моделирования

Для проведения экспериментальных исследований использовался комплекс информационноизмерительной аппаратуры на базе АЦП L-CardE-1440 c регистрирующим устройством. При проведении испытаний определялись вертикальные ускорения опорных катков машины при плавном разгоне от минимально устойчивой скорости до скорости 50 км/ч. В качестве первичных преобразователей использовались однокомпонентные датчики ускорений (АТ 1105-60А), устанв-ливаемые на стебле балансиров. Номинальный коэффициент трансформации в диапазоне измерения акселерометров ∓588 м/с2 (∓60g) составляет 10,2 mV/(m/s2), полоса пропускания от 0 до 700 Гц, нелинейность выходной характеристики не более 0,5 %. Производитель – ОАО «Арзамасское научно-производственное предприятие «ТЕМП-АВИА», г. Арзамас, Россия. Обработка экспериментальных данных выполнялась в программном пакете Power Graph Professional 3.3.8. На рис. 7 приведен пример реализации процесса высокочастотного нагружения опорного катка гусеничной машины.

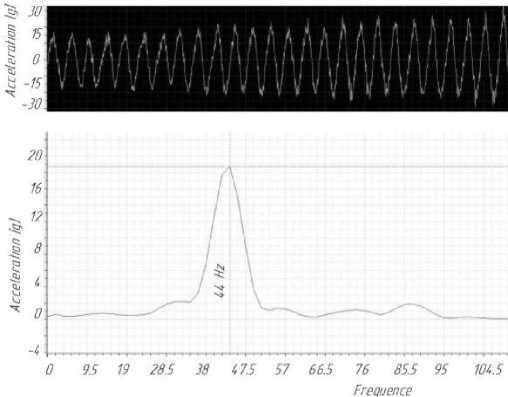
Рис. 7. Пример реализации процесса высокочастотного нагружения опорного катка гусеничной машины

Результаты испытаний показали, что ускорения на «траковой» частоте достигают 300 м/c2 и выше. С учетом значения неподрессоренной массы, дополнительная высокочастотная нагрузка, действующая на каток, достигает величины статического нагружения. Результаты выполненных экспериментов подтвердили гипотезу возникновения резонансных колебаний, реализуемых, как минимум, в одном скоростном диапазоне, соответствующем параметру диаграммы Айнса-Стретта a=1 . Это наиболее опасный случай проявления параметрического резонанса. При этом наибольшие амплитуды виброускорений были зарегистрированы на скоростях от 20 до 28 км/ч, что соответствует «траковой» частоте от 37 до 52 Гц.

Численное моделирование выполнялось в пакете MSC Nastran. Расчет выполнен в SOL 101: нелинейном блоке статического анализа, размер конечных элементов варьируется от 2 до 5 мм. При моделировании приняты условия нагружения опорного катка силой 15 кН. Расчетная схема определения напряженно-деформированного состояния соответствует условиям проведения эксперимента, результаты которого приведены на рис. 1. При моделировании напряженно-деформированного состояния и определении глубины модуляции упругого взаимодействия использовались два варианта конструкции гусениц. Результаты представлены в виде графиков на рис. 8. Области a и b демонстрируют разницу упругого сближения «шина – обрезиненная беговая дорожка» по длине гусеницы график 1 соответствует прототипу, график 2 – модернизированной конструкции [20].

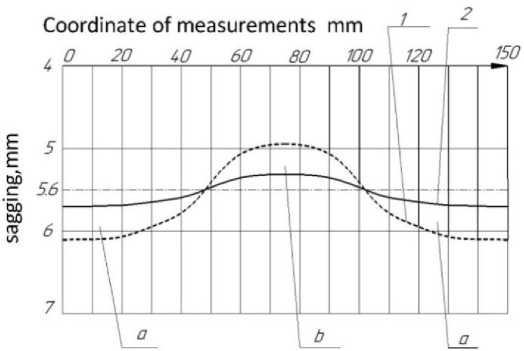
Рис. 8. Результаты численного моделирования двух вариантов гусениц 1 – серийный вариант; 2 – модернизированный вариант

В модернизированном варианте гусеницы требуемое снижение значения параметра ц (параметра ℎ в терминах диаграммы Айнса-Стретта) достигается смещением полутраков гусеницы на 10 мм [20]. Такой же результат может быть достигнут при зигзагообразном выполнении каждого полутрака гусеницы. В обоих случаях ограничением при смещении полутраков является условие ненатыкания смежных траков при прохождении по окружности ведущего колеса гусеничной машины. Достигнутый уровень «сглаживания – уменьшения» глубины модуляции jU позволяет прогнозировать исключение возникновения параметрических резонансов, вследствие чего можно ожидать существенного снижения уровня динамической и тепловой нагруженности шин опорных катков.

Выводы

• 1)    разработанный комплекс конечно-элементных и твердотельных математических моделей позволил подтвердить гипотезу о возникновении параметрических резонансов неподрессоренных элементов конструкции ходовой части гусеничной машины при движении по твердым грунтам;

• 2)    результаты выполненных экспериментальных исследований подтвердили адекватность разработанных математических моделей;

• 3)    результаты расчетно-экспериментального исследования позволили:

• –    определить зоны неустойчивости полученного периодического решения, характеризующего процесс движения опорного катка по беговой дорожке;

• –    обосновать и определить требуемые значения упруго-инерционных показателей системы «шина опорного катка – гусеница» при двухпараметрическом регулировании процесса их динамического взаимодействия.