Исследование параунитарных матриц для реализации цифровой обработки сигналов в конечных полях

Одной из весьма актуальных задач, стоящих перед современной наукой, является задача создания высокопроизводительных устройств цифровой обработки сигналов (ЦОС). Использование наборов фильтров в значительной степени поспособствовало развитию этого направления. Существует два способа разложения сигнала при помощи фильтров [1]: прямое разложение и полифаз-ное разложение.

Рис. 1. Дискретное вейвлет-преобразование сигнала

На рис. 1 изображен набор фильтров дискретного вейвлет-преобразования (ДВП) сигнала [2]. Это типичный пример прямого разложения сигнала при помощи двухканального набора фильтров. Разработке и проектированию фильтров, осуществляющих полифазное разложение сигнала,в отечественной литературе уделяется меньше внимания.

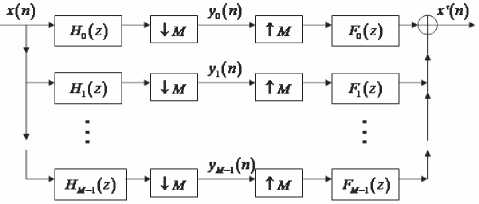
Рис. 2. M -канальный набор фильтров

В ЦОС значительный интерес представляют фильтры с числом каналов, большим двух. На рис. 2 изображен набор фильтров, состоящий из M каналов. Его представление в форме полифазной матрицы (polyphase matrix) показано на рис. 3.

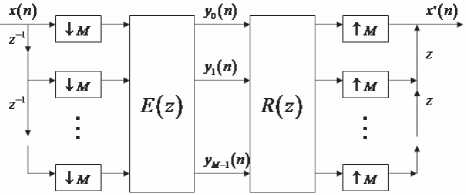
Рис. 3. Полифазное представление M -канального набора фильтров

Вопросы построения и реализации таких наборов фильтров в полях действительных и комплексных чисел изучены достаточно хорошо. Набор фильтров называется параунитарным, если его полифазная матрица является параунитарной, то есть Е^Е^Н для всех (У, где верхний индекс t означает сопряженное транспонирование [3]. Если положить R(e/ffl) = Et(eA1'),то набор фильтров будет обладать свойством точной реконструкции сигнала. Важным преимуществом параунитарных наборов фильтров является тот факт, что свойство точной реконструкции сигнала достигается с использованием фильтров конечной импульсной характеристики (КИХ-фильтров), а также то, что синтезирующие фильтры получаются с помощью простого преобразования анализирующих фильтров.

Целью настоящей статьи является изучение свойства параунитарности матриц в полях GF^p") . С помощью таких матриц можно будет создавать наборы фильтров со свойством точной реконструкции сигнала, функционирующие в арифметике конечных полей. В случае /7 = 1 построенные системы можно будет использовать для создания устройств, функционирующих в системе остаточных классов (СОК). Случай n > 1 можно будет использовать для разработки методов фильтрации в полиномиальной системе остаточных классов (ПСОК). Указанные системы обладают важным преимуществом перед традиционной позиционной системой счисления (ПСС): свойством параллельной обработки сигнала [4-5]. Это делает задачу исследования весьма актуальной.

Параунитарные матрицы в GF^p”^

Речь пойдет о квадратных матрицах размера MxM . Единичную матрицу будем обозначать

Утверждение 2. Произведение двух парауни-тарных MxM матриц над GF^p'^ будет пара-унитарной матрицей.

Доказательство. Пусть E, (z) и Е_э (z) - две параунитарные MxM матрицы в GF(p"A . Тогда

[E,(z-|)E2(z-,))r(E,(z)E2(z))

(z'^Ef (z"1)ei(z))e2(z)

(z-’)lE2(z) = I.

Очевидно, что по индукции можно показать, что и произведение любого конечного числа пара-унитарных MxM матриц будет параунитарной матрицей. Введем символ к = V^rV для произвольного вектора V с целью введения числовой характеристики вектора, аналогичной норме в евклидовых и унитарных векторных пространствах. Особенностью конечных полей является тот факт, что в полях GF(/H существуют векторы V^O – такие, что Z_v = V^rv = 0. Через I" обозначим мультипликативный обратный элемент поля GF(p”} для .

Лемма 1. Матрица вида v = /;’w в поле GF^p"^ для такого вектора v , что , обладает следующим свойством:

(0 0 ••■ 1)

y = y^T =y^Ty.           (3)

Нумерацию столбцов и строк будем вести от 0 до M-\ . Буквами U, V и т. д. обозначим векторы-столбцы элементов поля GF^ . Нулевой вектор обозначим

Доказательство.

V^r = ^I;W )" = /;’ (v^r f (vf = l;W = V, v^rv = vv = i;Wi;W = i>V = v.

Сформулированная лемма поможет для доказательства следующей теоремы.

Теорема 1. Возьмем вектор v в GF^ , такой, что l_v = v^rv ^ 0 . Тогда матрица s -ro порядка

N

Рациональная матрица вида ^Е(-)=£^е(ф-^А', где c ( к ) - квадратные MxM матрицы над полем GF(p”) , называется параунитарной MxM матрицей, если

Er(z-')E(z) = I.

Число N будем называть порядком системы.

Утверждение 1. Для параунитарной матри-/V цы E(2)=EeW- должно выполняться сле-k=0

дующее соотношение:

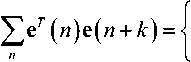
I, k = 0

.

Доказательство этого утверждения см. в [6].

D_$ (z) = I-/_V'vv^r + z 7_v'w^r (4)

будет параунитарной в        .

Доказательство. Обозначим v = i;'w . Учитывая свойство матрицы V (лемма 1), можем записать:

D;(z-')D5.(z) =

= (l - /у'^ууГ + z^sl^'vv^T ) (l - /”'vv^r + z"4^'vv^T ) = = (l - V + z^jv)^r (l - V + z’^sv) -= (l-V^r +z'V⁷J(l-V + z^'V) = I-V⁷ + +z^$V^r - V + V^rV - z^sV^T V + z’^sV - z~^sV^T V + +z^s-^sV^rV = (I - V⁷ - V + V^rV + v^rv) + +z^s (V^r - V^rv) + z"^s (V - V^rv) = I.

Эта теорема является обобщением факта о па-раунитарных матрицах первого порядка простого поля Галуа, указанного в [6]. Если в сформулированной теореме положить s = 1 , то мы получим параунитарную матрицу первого порядка. Пара-унитарные матрицы первого порядка играют важную роль в факторизации параунитарных систем (подробнее см. [6-8]).

Пример 1. Построим параунитарную 4x4 матрицу пятого порядка в поле GF (2³). Для этого сначала построим поле GF(2³), используя примитивный многочлен x^J + x +1 поля GF (2). Элементы конечного поля F_q=GF^ с порядком q , где q = p", p – простое число, называемое характеристикой, а n – натуральное, называемое разрядностью, могут иметь следующие представления, образующие изоморфные поля: см. таблицу 1 [9].

• 1.    Целочисленное представление 0; 1 ... q -1 соответствует последовательной нумерации элементов поля.

• 2.    Степенное представление a¹, где a – примитивный элемент, i e p.

• 3.    Полиномиальное представление

• 4.    Векторное представление a = (a„_₁ ...ap,a₀) в базисе a°; a¹ ... a" ¹, где 0 <  a,< p , i = 0,1,...,и -1.

g(x) = У^а'х' = a^x"-1 + ... + a1x + a0 ,

/=0

a, gFp, i = 0A,...,n-\.

Таблица 1. Элементы поля GF(2³)

g g § к F T 0 О CD CL C	Ct Cl c s 0 g 5 H и	О I S X CQ ° 8 Cl 0 1 0 c C	Ct CL О с к О w u О m
0	0	0	ООО
1	a	a	010
2	a2	a2	100
3	a2	a + 1	011
4	a4	ома	110
5	a5	a2 + a + l	111
6	a6	a2 +1	101
7	a?	1	001

Для цифровой обработки информации применяются, как правило, поля характеристики 2:

F,„ =GF(2"). В таблице 1 приведены основные представления элементов поля GF (23) для полинома x3 + x +1.

Положим v = |^1 a a? zz3] ,

Z_v = v^rv = |j a a²

a

= 1 + a² + a⁴ + a⁶ = a⁴ ^ 0,

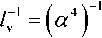
Тогда

n = i;xnV = a3 a a2 [1 a a2 zz3 = По теореме 1 0 Z Л     0 1 D3 z) = 3V ’    0 0 v0 0 +z 6Z + tZ3Z~5 6 a4 + a4z"s c r a3 a4 a5 va6 матр 0 0 0 0 1 0 0 1 a -5 « a val x4 -va z4 +a a3 a4 a5 a6 1 ица ) I a a a 4 -5 z 5z”5 a5 a6^ a6 1 1 a a a2 ? 3       4 a,   a   a- 4       5 01   a   a a5  a6   1 »6   1    a 4 а5 аьУ 5 a6 1 5    1    a a a2 y a5 + o’ z”3 a6 + a6z"3 a6' 1 + a a2 y a6 + a6 z”5 1 + z’5 a5 + a5z 5 a6 + a va6 + a6 z”5 1 + z 6z”5 -5 z""5 a + az”5 a + az”5 a6 +a2z”5 y будет параунитарной 4x4 матрицей пятого по- рядка в поле GF (23

Построение наборов фильтров в

GF^p")

Вернемся к схеме, изображенной на рис. 3. Как было указано выше, набор фильтров, изображенный на ней, называется параунитарным, если его полифазная матрица параунитарна. В GF^p"^ это значит, что E^r(z-¹)E(z) = I. Если параунитарная матрица E(z) известна, то матрицу r(z) полагаем

R(z) = E^r(z-').              (5)

Переход от полифазного набора фильтров к набору фильтров, осуществляющему прямое преобразование сигнала (см. рис. 2), осуществляется по следующим формулам [3]:

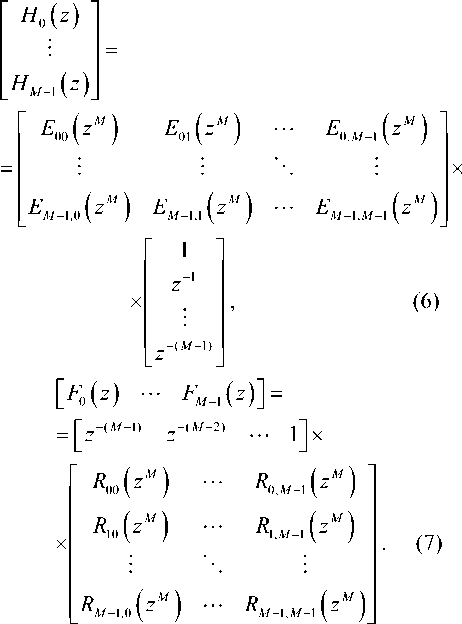
Наиболее широкое применение в ЦОС находят двухканальные наборы фильтров, например, для реализации вейвлет-преобразования сигнала. Использование наборов фильтров с числом каналов, большим двух, может иметь ряд преимуществ по сравнению с двухканальными. Например, при использовании в параллельно-организованной архитектуре системы ЦОС будет увеличено быстродействие за счет большего числа каналов, выполняемых параллельно и независимо друг от друга. На рис. 1 показан набор фильтров, осуществляющий вейвлет-преобразование сигнала. Для вычисления коэффициентов каждой последующей октавы необходимо дождаться окончания операции фильтрации в предыдущей. Это создает последовательность действий в выполнении операций, а значит, замедляет быстродействие. Если с аналогичной целью использовать набор фильтров с числом каналов, большим двух, то очевидно, что процесс получения коэффициентов разложения сигнала произойдет быстрее.

С другой стороны, интерес представляют наборы фильтров в полях GF (2"). Такие наборы фильтров могут быть сравнительно просто реализованы в системах ЦОС, функционирующих в двоичной арифметике. Операция умножения двух элементов конечного поля GF (2") задается при помощи простейших логических операций, чего нельзя сказать о полях GF^ при p>1.

Заключение

Рассмотрена теория параунитарных матриц в поле GF^p”^ . Условие, выведенное в теореме 1, позволяет строить параунитарные матрицы любого порядка и размера над произвольным конечным полем. Построенные таким образом параунитар-ные матрицы могут быть использованы для разработки многоканальных наборов фильтров. Многоканальные наборы фильтров должны обладать более высоким быстродействием по сравнению с двухканальными, однако этот вопрос требует дальнейшего изучения и экспериментальной проверки.