Исследование пеленгационного рельефа, формируемого линейной антенной решеткой при обработке сигналов по методу Кейпона

В связи с широким распространением радиоэлектронных средств различного назначения и соответствующим усложнением радиоэлектронной обстановки приобретают особую актуальность вопросы применения методов сверхразрешения для пространственной обработки сигналов в антенных системах. Данное обстоятельство определяется тем, что использование указанных методов позволяет получить для источников сигналов угловое разрешение более высокой степени, чем определяемое размерами апертуры антенны в соответствии с критерием Рэлея [1–3].

Графическое представление характерного пеленгационного рельефа (ПР) линейной антенной решетки изотропных излучателей при использовании метода Кейпона приведено на рис. 1 (кривая 1). Для сравнения кривой 2 на этом рисунке показан ПР, формируемый данной антенной при использовании классического метода пространственной обработки сигналов.

Приведенные зависимости иллюстрируют значительные возможности по повышению разрешающей способности антенных систем при использовании методов сверхразрешения. Обзор указанных алгоритмов приведен в работах [1–6], где достаточно подробно исследованы характеристики антенн, достигаемые при применении алгоритмов сверхразрешения. В работе [5], в частности, рассмотрены зависимости разрешающей способности в антенных решетках (АР) от мощности сигналов и числа излучателей. В данной статье проводится анализ взаимосвязи потенциально достижимых параметров ПР при пеленговании одного источника сигнала с параметрами антенны (число излучателей) и принимаемого сигнала (мощности и направления прихода).

• 1.    Математическая модель линейной адаптивной антенной решетки с пространственной обработкой сигнала по методу Кейпона

Рассмотрим линейную АР, состоящую из N изотропных излучателей, расположенных на расстоянии d друг от друга. Пеленгационный рельеф, формируемый антенной при использовании метода Кейпона, описывается соотношением [7]

P ( ф ) = [ v ( 9 ) T R ^{- 1} v ( Q ) * ]^- 1 ,                         (1)

где v ( ф ) — сканирующий вектор АР; R — корреляционная матрица сигналов; « T », «*» – соответственно обозначения операций транспонирования и комплексного сопряжения.

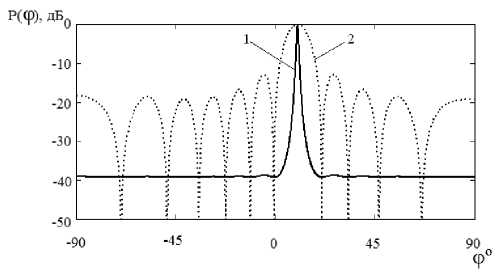
Рис. 1. Пеленгационный рельеф 9-элементной линейной АР (кривая 1 – при использовании метода Кейпона, кривая 2 – классический метод пространственной обработки)

P ( Ф 1 ) = U ²/ о ² .

При фазировании АР в произвольном направлении вне главного максимума ПР из формулы (4) получаем

P ( ф ) = N ^{- 1} .

Корреляционная матрица может быть записана следующи м образом

R о ² Е + U ² s^) * s ( ф ₁) T ,                      (2)

где о — мощность теплового шума в канале АР; 2

U – мощность пеленгуемого сигнала; E – единичная матрица размерности N ; Ф 1 - направление прихода пеленгуемого сигнала, отсчитываемое от нормали к линии расположения излучателей.

Для линейной АР элементы векторов определяются соотношениями:

v n ( ф ) = exp( - ikx n sin ф ),

Sn (Ф1) = exp(-ik^n sin Ф1), в которых k – волновое число; x^n – координата n-го излучателя (n = 1,..., N).

Данная формула получается непосредственно из (4) с учетом того, что F ² ( ф ) <<  N ² . Таким образом, уровень ПР вне главного максимума, формируемый при использовании метода Кей-пона, является постоянным. Максимальное значение ПР превосходит данный уровень в NU ²/ о ² раз. При использовании классического метода формирования ПР отношение максимального значения к уровню боковых лепестков не зависит ни от числа излучателей, ни от мощности принимаемого сигнала.

Проведем оценку ширины главного максимума ПР, формируемого при использовании метода Кейпона. С учетом выражений (1) и (3) угловая зависимость ПР может быть представлена

в виде

P ( Ф ) =

N - F^U /V

1 + NU ²/ о ²

- 1

2. Результаты исследований

где F ² ( ф ) — квадрат амплитудной диаграммы направленности (ДН) в направлении ф линейной АР, сфазированной в направлении ф 1 .

Для линейной АР изотропных излучателей имеем

Представим обратную корреляционную рицу в виде [8]

мат-

7( ф )

sin ² ( kdN sin у/2 ) sin ² ( kd sin у /2 )

R

¹ = о^{- 2}

( _E - U 2,'о²

_s 1 + NU ² / о ²

------:------^ ) s(Ф1) s(Ф1)T

J

.

Подстановка соотношения (3) в выражение (1) позволяет дать следующее представление для ПР:

P ( ф ) = N

-

F ² ( ф ) U ²/о² 1 + NU ²/ о ²

- 1

,

где F ² ( ф ) — ДН линейной АР по мощности.

При фазировании АР на источник пеленгуемого сигнала, что соответствует выбору сканирующего вектора v = s^ ) * , F ² ( ф ) = N ² и уровень ПР с учетом соотношений (1) и (4) определяются

где у = ф - ф1.

В области главного максимума (при малых значениях у и условии kdN у /2 <  1) F 1² ( ф ) может быть представлена зависимостью

Т 2 ( ф ) « N ² - к ² d ² N ⁴ у ²/12 .

С учетом последнего соотношения угловая зависимость ПР в области главного максимума может быть определена с помощью соотношения

P ( ф ) = U ²/ о ² [ 1 + к ² d ² N 3 у ² U 2/ 12 о ² J - ¹ .      (10)

следующим выражением:

Последнее соотношение позволяет легко определить ширину главного максимума ПР по уровню половинной мощности:

P ( Ф 1 ) =

N ² U ²/ о ² 1 + NU ²/ о ²

которое при условии NU /о >>  1 после простых преобразований приводится к виду

^Ау 0,5 = I ч 91 9 .                            ⁽¹¹⁾

kd^N ³ U ²/ о ²

Таким образом, приведенные в статье соотношения позволяют для случая пеленгования

одного источника установить закономерности,

связывающие параметры линейной АР с параметрами ПР.

Заключение

Использование метода Кейпона при формировании ПР линейной АР позволяет добиться сужения главного лепестка ПР по сравнению с классическим методом и обеспечить более высокий уровень отношения значений ПР в направлении главного максимума и вне главного лепестка. При этом уровень ПР вне главного максимума является практически постоянным. На основе аналитических преобразований обратной матрицы получены следующие закономерности:

– уровень максимального значения ПР в направлении на источник сигнала превосходит уровень ПР в других направлениях в NU ² σ ² раз, в то время как при использовании классического метода формирования ПР соотношение между максимальным значением ПР и средним уровнем ПР не зависит ни от числа излучателей, ни от мощности пеленгуемого сигнала;

– ширина главного максимума ПР при использовании метода Кейпона обратно пропорциональна относительной мощности пеленгуемого сигнала, в то время как для классического метода не зависит от этого параметра;

– при увеличении числа излучателей линейной АР ширина главного максимума ПР уменьшается по закону N - ^{3 2} (при использовании классического метода – по закону N - ¹ ).