Исследование плоских симметричных антенн с линейно-расширяющимся раскрывом для антенных решеток

Антенны и антенные устройства в радиотехнических системах являются важнейшим функциональным звеном, характеристики которого во многом определяют характеристики остальных функциональных блоков системы. В связи с чем, разработка и исследование характеристик новых антенн и антенных устройств на их основе (в том числе СВЧ-диапазона) представляет повышенный интерес и является актуальным. Следует отметить важность разработки адекватных математических моделей для проектируемых антенн, подтвержденных получаемыми экспериментальными данными, позволяющих заранее рассчитывать и прогнозировать их важнейшие характеристики, что также является востребованным и актуальным.

В данной работе исследуются плоские антенны (рис. 1), выполненные в виде симметричных ще-

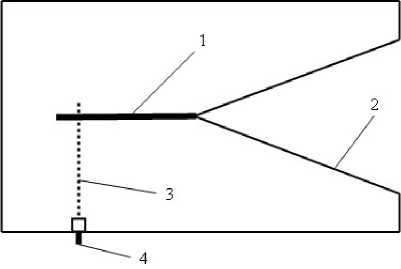
Рис. 1. Внешний вид исследовавшихся антенн: 1 – симметричная щелевая линия; 2 – расширяющаяся СЩЛ; 3 – питающая микрополосковая линия; 4 – коаксиальный разъем лей с линейно расширяющимся выходом (раскрывом), вырезанных в металлических пластинах с высокой проводимостью (медь, алюминий), толщиной порядка 0,3 мм, без диэлектрической подложки (2, рис. 1), которые предполагается использовать в составе дисковых антенных решеток. В данном случае питание всех антенн производилось через коаксиальный разъем (4, рис. 1), микрополосковую линию передачи (3, рис. 1) и симметричную щелевую линию (1, рис. 1).

Для разработки электродинамических моделей исследовавшихся антенн воспользуемся основными положениями из [1]. Для расчета диаграмм направленности (ДН) антенн, у которых изменение поперечного сечения раскрыва является линейным, произведем его регуляризацию, как показано на рис. 2. Такая регуляризация для конечного числа участков позволяет применить методику разработки моделей, приведенную в [2; 3] для каждого регулярного участка, и по их суммарному вкладу рассчитать ДН всей антенны.

Для подобной ступенчатой аппроксимации нерегулярной структуры шаг увеличения ширины щели должен быть много меньшим четверти длины волны [2]:

X wn - wn—i = wn+i - wn = Aw << , (1)

где w_n – ширина щели n -го регулярного участка направляющей структуры антенны; X_o — дли-

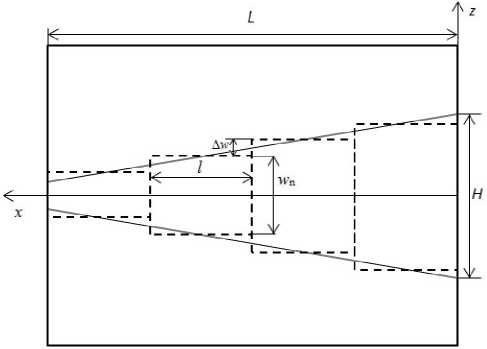
Рис. 2. Аппроксимация линейно расширяющегося раскрыва антенны регулярными участками

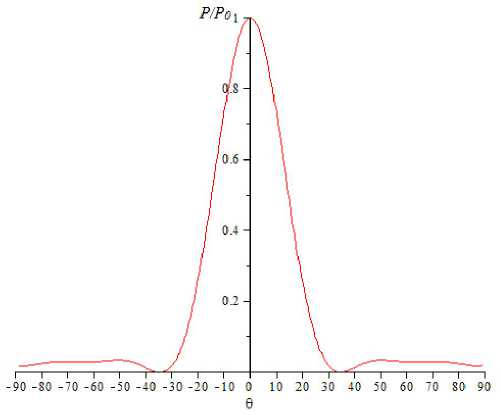
Рис. 3. Рассчитанная диаграмма направленности исследуемой антенны для случая L = 150 мм, H = 60 мм

на волны электромагнитных колебаний на входе антенны.

При этом результирующее поле в дальней зоне будет определяться суммированием вклада в излучение, вносимого каждым регулярным участком, согласно выражению [1]:

N

E (О, ф) = £ E n (О, ф),                            (2)

n = 1

где E n (О, ф) — вклад в поле дальней зоны n -м участком; О, ф — угловые координаты в Е-плос-кости и Н-плоскости ДН, соответственно.

Для сохранения условия бегущей вдоль направляющей структуры антенны волны необходимо, чтобы мощность, проходящая через каждый регулярный участок, оставалась постоянной

P n - 1 = P n = P n + 1 = const .                      (3)

Мощность, проходящая вдоль n -го участка регулярной структуры, может быть определена как

P n = V n ,                                     (4)

Zn где Vn – разность потенциалов на n-м регулярном участке, а Zn – его волновое сопротивление.

Выражение (2), с учетом (3), (4) и заменой V_n на поперечную составляющую поля регулярной симметричной щелевой линией (СЩЛ), положив P_n = 1 [1], можно записать:

N

E (О, Ф) = £ Z n E E n n (О, Ф),                     (5)

n = 1

где E _{0 n} – поле излучения n -го регулярного участка, которое может быть определено по какой-либо модели антенны с щелью постоянной ширины, а Z_n можно определить по формуле [1]:

Z n

ln

к

60 л2

(

2 H

--⁺ w

.

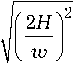
-1

Процедура ступенчатой аппроксимации может быть автоматизирована или произведена вручную. Произведенные расчеты показывают, что

результаты хорошо сходятся, когда значение A w = Х₀ / 8 [4; 5].

Как показано в [1], поперечная компонента электрической напряженности электромагнитно-

го поля для n -го регулярного участка антенны (рис. 2) определяется следующим выражением:

j toe w sin ф e ^{jk 0т}

E О (О, Ф) =  ----------------х

4п² r

w /2 e jk 0 ² ' cos О

X j

- w /2

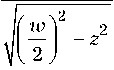
n

j

1 + e ⁴ F

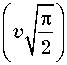
Здесь

L dz'j ejk0x'sin 6cosФ ekxx' x

n

V2 e j 4

-

e

■ П 2 jv

dx '.

F ( v ) = j e — j- 2 dt

– интеграл Френеля;

2k_nx' sin О(1 + cos ф) v =     ⁰-------------------;

n

to — частота электромагнитных колебаний на входе антенны; k ₀ – волновое число; j – мнимая единица; t – время.

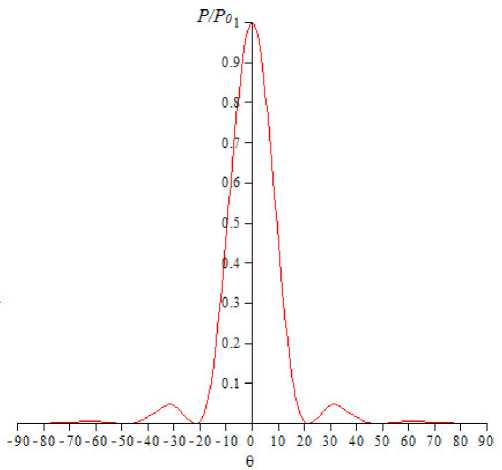
Рис. 4. Рассчитанная диаграмма направленности исследуемой антенны для случая L = 150 мм, H = 90 мм

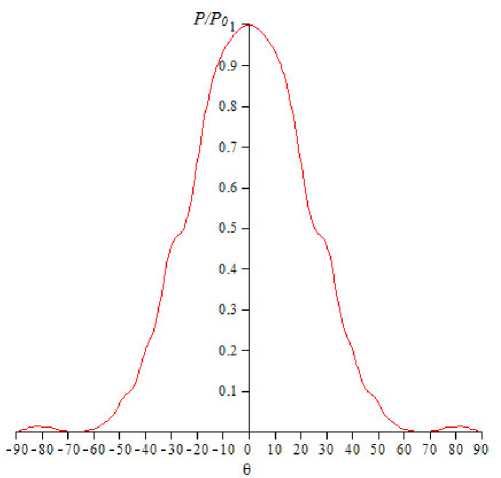
Рис. 5. Рассчитанная диаграмма направленности исследуемой антенны для случая L = 150 мм, H = 30 мм

Интегралы в расчетных формулах находятся численно, а построение ДН в случае постоянной ширины щели в главных плоскостях производится нормированием результатов при 9 = п для Е-плоскости и ф = п /2 для Н-плоскости [6].

Расчеты ДН производились для антенн, имевших длину L в пределах (1 ^ 5X), и ширину раскрыва Н в пределах (1 ^ 3Х) мм, на частоте 10 ГГц, для Е-плоскости электромагнитных колебаний. На рис. 3 приведена диаграмма направленности, полученная в результате моделирования с использованием (5)–(7) для случая L = 150 мм и Н = 60 мм. Видно, что ширина ДН по уровню половинной мощности составляет порядка 30°, а уровень боковых лепестков (УБЛ) имеет значение порядка 0,05 от мощности излучения непосредственно перед антенной (при 9 = 0).

В качестве проверки адекватности полученных результатов также производилось построение ДН для одного регулярного участка (с n = 0). Эти ДН сравнивались с экспериментально полученными результатами для регулярной антенны в [7]. Сравнительный анализ опытных данных и результатов моделирования показал, что имевшие при этом место расхождения ДН были незначительными (в пределах 5 ^). Наилучшим образом результаты совпадают в случае, когда значение Aw = X0 / 8. Это свидетельствует об адекватности полученных модельных представлений и возможности их использования для моделирования ДН подобных антенн с любыми параметрами, а также ДН более сложных антенных систем (решеток) на их основе.

Расчет ДН исследуемой антенны при изменении ширины раскрыва (размера Н , при постоянной длине L = 5X = 150 мм) в большую ( H = 3X = 90 мм) и меньшую ( H = X = 30 мм, рис. 5) сторону показал следующее. При увеличении размера антенны Н , главный лепесток ДН существенно сужается (рис. 4), а ее ширина по уровню половинной мощности составляет порядка 20°. При уменьшении размера Н , главный лепесток ДН существенно расширяется (рис. 5), а ее ширина по уровню половинной мощности составляет порядка 46°.

Из этих графиков также видно, что для постоянной длины антенны L при увеличении ее размера Н , УБЛ возрастает, но не превышает уровня 0,1 от максимальной мощности излучения.

Для проведения натурного эксперимента был сконструирован набор антенн, у которых, также, при длине антенны L равном 150 мм (5X) ширина раскрыва Н изменялась в пределах (1 ^ 3X). Ширина щелевой линии w ( 1 , рис. 1) для всех антенн выбиралась одинаковой ( w = 3 мм). Проектирование антенн с учетом их электродинамических свойств производилось с учетом основных положений, изложенных в [8–10], измерение их диаграмм направленности производилось на установке, описанной в [11; 12].

На рис. 6–8 представлены диаграммы направленности антенн в Е- и Н - плоскостях с шириной раскрыва Н = 30 мм (1X), 60 мм (2X) и 90 мм (3X),

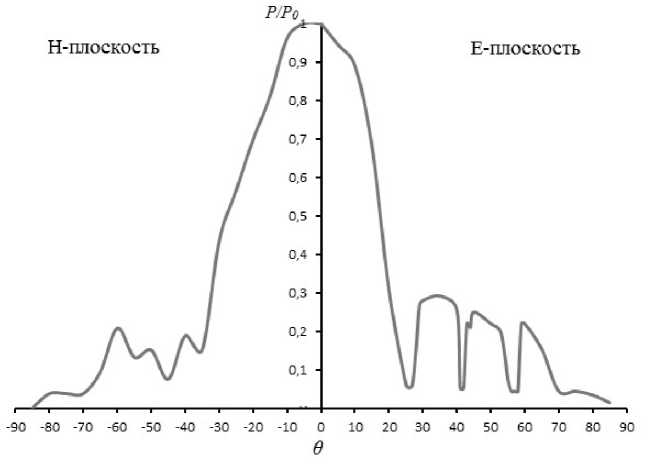
Рис. 6. Экспериментально измеренная диаграмма направленности исследуемой антенны для случая L = 150 мм, H = 30 мм

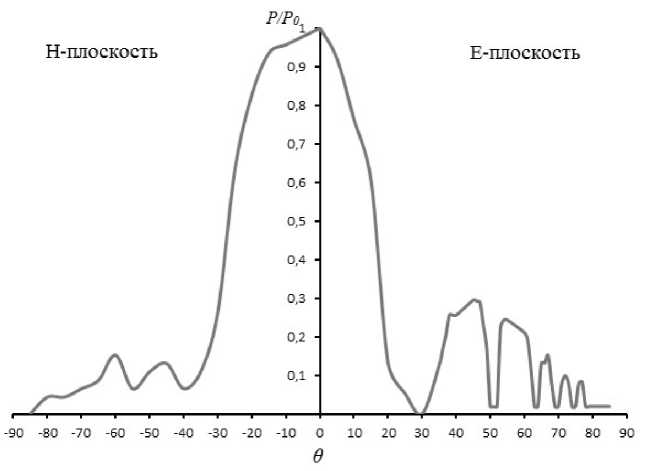
Рис. 7. Экспериментально измеренная диаграмма направленности исследуемой антенны для случая L = 150 мм, H = 60 мм

соответственно. Следует отметить, что форма ДН, измеренных на частоте 10 ГГц со х ранялась практически неизменной в диапазоне частот 5,9– 12,5 Г Г ц.

Из анализа экспериментально измеренных ДН видно, что при увеличении раскрыва антенны, их главный лепесток, как и в случае расчетных ДН (для Е-плоскости), сужается. При этом ширина экспериментально полученных ДН по половинной мощности составляла порядка 48° — в случае Н = 30 мм (1Х), 32° — в случае Н = 60 мм (2Х) и 20° — в случае Н = 90 мм (3Х), что хорошо согласуется с результатами расчета. Уровень боковые лепестков у экспериментально полученных ДН несколько выше, чем у расчетных и не превышал 0,3 от максимальной мощности.

Из графиков рис. 6–8 также видно, что в Н-плоскости главные лепестки ДН для одних и тех же значений раскрыва антенн несколько шире, чем в Е-плоскости. При этом их ширина, при изменении раскрыва антенн, оставалась практически неизменной. Кроме того, в Н-плоскости имеет место тенденция к увеличению УБЛ при увеличении раскрыва антенны, также, как в случае расчетных ДН.

Из полученных расчетных и экспериментальных результатов исследования плоских симметричных антенн с линейно расширяющимся выходом видно, что имеется явная зависимость ширины главного лепестка ДН в Е-плоскости от угла раскрыва (размера Н ). Это позволяет использовать данные разновидности антенн

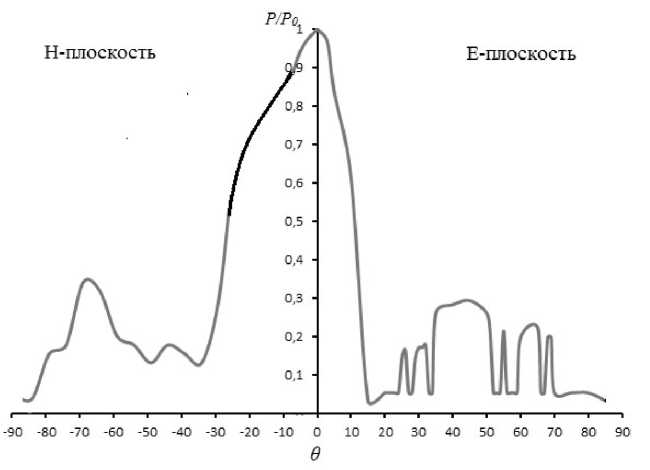
Рис. 8. Экспериментально измеренная диаграмма направленности исследуемой антенны для случая L = 150 мм, H = 90 мм

в качестве базовых элементов в составе более сложных антенных системах, таких как дисковые антенные решетки [7], для улучшения и оптимизации их электродинамических характеристик. Полученные модельные представления позволяют заранее рассчитывать оптимальные геометрические размеры базовых элементов для соответствующих разрабатываемых новых перспективных антенных систем в области радио-, видеолокации, при разработке охранных систем и других радиоэлектронных устройств.