Исследование подрессоривания трелевочной системы

Вибронагруженность трелевочной системы в вертикальной плоскости симметрии определяется структурой подрессоривания, параметрами и характеристиками упруго-диссипативных связей, уровнем и характером неровности волока (почвы).

На рисунке 1 приведена упрощенная модель двухступенчатого подрессоривания коника (КЗУ) и трактора Т40-Л с пачкой хлыстов, где: m п , m 1 , m 2 – подрессоренные массы жесткой пачки с опорной базой l , приведенной к точке 1 массой пачки ( m пк ) с массой КЗУ ( m _кз), массой полурамы ( m _п р ) с колесной парой ( m кп ), ( m 1 = m П + m _кз, m 2 = m пр =( J _т + 22

+ m _т / 1 )/ / _т , / т = / 1 + / 2 ); C z , Р z , c п , Р п — параметры жесткости и диссипации подвеса КЗу и шин КП. Приведенная к точке <К> масса пачки определяется из баланса кинетических энергий для z , = l x ^ф:

¹ Авторы — соответственно профессор кафедры теоретической и строительной механики и студент V курса Санкт-Петербургской государственной лесотехнической академии, кафедра технологии лесозаготовительных производств.

2T = Jo

Трактор Т40-Л имеет инерционную квазисимметрию, J _r ~ m _т / 1 / 2 относительно осей z ₀, z 1 . Поэтому вертикальные его колебания разделяются на независимые, одномерные с приведенными к осям z _o, z 1 массами: m п ^0,1 ) = ( J _т + m _т / 1 0 ) I l .2 .

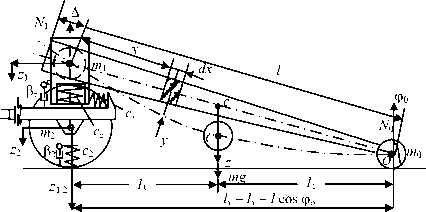
Рис. 1. Расчетная модель подрессоривания трелевочной системы

Уравнения состояния введенной системы для жесткой пачки составим по рисунку 1 в новых координатах деформациях связей x1 = z1 -z2, x2 = z2 -zк :

z2 = x2 + zк, z1 = X1 + z2 = X1 + x2 + zк.

Тогда кинетическая и потенциальная энергии системы:

2 Т = m ^ z ^ + m 2 z 2 =

= ^m1⁽ x + x 2 + ^ )² + m 2⁽ x 2 ⁺ ^&к ^{) 2 ,}

2 П = C 1 x 2 + c 2 x 2 ,  2 R = Р 1 x 2 + Р2- x 2 .

Вводя их в уравнения Лагранжа d d T d T 8ПdR

----+—+— = Q j , dt dx i dX i    dX i d ;& i ^J

получим:

I ^m 1 ^x 1 ^{+ m} X ^x 2 ^+p 2 ^x 2 ⁺ c 2 ^x 2 =^- m X ^z к .

Вычитая из второго уравнения первое, запишем другое представление

' m i ^{( x} i + x 2 ) + P ijq + qx i = - m i z k ,

" ^m 2 ^x2 - P i- x i - c i- x i + P 2 ^x 2 ^{+ c} 2 ^x 2 = (5 б )

l = ^- m 2 z к .

или в операторно-матричном виде при d / dt = p :

m i P 2 +P i P ⁺ c i   m i P 2 I^- m i P 2 z k (P)

m2 P 2 + i 2

• ^- ( P i P + c i )            i- m 2 P ² z k ⁽ P )

I             +P2 P+c2\J

При жестком креплении коника на полураме ( C z = да ) уравнения (5) упрощаются:

m^ X2 +PX2 + cx 2 = -m2 zk.

Для передаточной функции П 2 = x 2 ( р ) / Z к (р ) =

• —m ^ p

=       2          и спектральной плотности не- m^p2+Pp+c ровности пути Sк = В4V3 / to4 дисперсии деформации, скорости и реакции подвеса по формулам Винера – Хинчина равны:

n да

Dx. = :НЫ i to )² d to | = B / C ₽ ,

• ² 2n -

  -да

B          2 2

^DX 2 = _{2 n} J । П 2⁽ i ^{to ) to} d ^{to |} = B / m ^{2 в} (8)

-да

D r = c ² D x 2 +P ² D x 2 = B [ c / p+p/ m 2 ],

B = 0,5 В ₄ v ³ = m ₂ .           (9)

Дисперсия реакции КП представляет здесь интегральную критериальную функцию вертикального взаимодействия шины и почвы (волока), т. е. функционал.

Он пропорционален возмущению пути В , сомножителю cm - и имеет минимум по параметру демпфирования Р ввиду его диссипативного и возмущающего действия: при Р = 0 или Р « да D_r = да .

Минимизация функционала D_r ( Р ) по параметру Р дает оптимальное значение последнего:

D r = min, d D_r / dp = 0, P = ^cm ₂ , Р кр = 2 Pm , 9 m =P / Р _к р = 0,5;

P = 2 9 ^cm ^ , m 2 = m i + m 2 ,     (i0)

где 9 = 0,5 — коэффициент диссипации (демпфирования) в долях от критического значения парциальной системы.

Значение 9 _m = 0,5 значительное. Поэтому при пологом минимуме его можно принимать за максимальное и допускать снижение в процессе наработки демпфера до 9 min — 0,3; А9 = 0,5...0,3. Однако в шинах внутреннее трение между волокнами резинокордной оболочки ограничено:

• 9 <  0,i; р <  0,2 Cm^ .       (ii)

Для максимальной диссипации (11) функционал (9) составляет:

D r = 5,2 В Cm2; = 5,2 В v , v ² = c / m ₂ , (i2)

где v — собственная частота подрессоренной массы m 2 .

Для исходных данных трактора Т40-Л ( m 2 = = 2820 кг, с = (i2/9) • i0⁵ Н/м, параметры (12, 11) равны:

v= 7 c / m ₂ = 2i/i8, c ^{— i},

P = 0,2V cm 2 = ii,6/i0,i кНс/м. (i3 а )

Очевидно, что при высокой жесткости шин завышена собственная частота подвеса. Упругая реакция шин задней колесной пары (КП,8) равна:

Q = c CT _x = V5 B v = (7,25/6,7) m ₂ V B _ч v ³, m ₂= 2820 кг.           (i3 б )

Она вырастает со скоростью движения v и ухудшением качества пути В _ч , пропорциональна подрессоренной массе.

Частотное уравнение системы (5, Р i = 0, р = i X )

А = mim 2[X 4-X 2(v2 +v2) +

2                              (14)

+ ^v l ^c 2 / ^m 2 ] = 0,

ν12=c1/m1,ν22=c2/m2, где ν1, ν2 — парциальные частоты системы. Отсюда частоты системы

2 λ ₁ ² ₂ =ν ₁ ² +ν ² ₂ ± ( ν ₁ ² +ν ²₂)² + 4 ν ₁ ² c ² . (15) ,                               m ₂

Для m ₁ = 1100 кг, m ₂ = 1720 кг, c ₁ = 190 ⋅ 10³, c ₂ = 900 ⋅ 10³ Н/м по формулам (14, 15):

ν ₁ ² = 170 ( ν ₁ = 13 c ^{- 1}), ν ² ₂ = 630( ν ₁ = 25, 2с ^{- 1}),

λ 1 = 11,6 с^–1, λ 2 = 25,8 с^–1.      (16)

Частоты системы близки одноименным парциальным значениям. При этом низшая частота, определяющая гибкость подвеса, ощутимо ниже (13 а ).

Передаточная функция (ПФ) радиальной деформации шин по матрице (6) и Крамеру для µ _о = 1 + m 1 / m 2 равна:

η2(p)=x2(p)=   Δ2(p)   = zк(р) Δ(p)⋅zк(р)      (17)

=- m ₂ p ²[ m ₁ p ² +µ _o( β ₁ p + c ₁)]/ Δ( p ) , Δ ( p ) = m ₁ m ₂ p ⁴ + p ³( m ₁ β ₂ +β ₁ m ₂) +

+ p ²( m ₁ c ₂ + c ₁ m ₂ +β ₁ β ₂) + p ( β ₁ c ₂ + (18)

+ c ₁ β ₂) + c ₁ c ₂.

Дисперсия радиальной реакции шин КП для спектра воздействия пути S _к = В _ч v ³ / ω ⁴ по Винеру – Хинчи-ну

22    B ч v ³ m 2 ² c 2 ²

D2 = c2 °x2 □    2n

^∞ m₁²(i ω )⁴ - (i ω )²( µ _o β ₁)² × d ω=

• _-∞          | Δ (i ω )|²

• =12 Bчv3m22c22⋅m1×

m₂ µ _o ² β ₁²/ β ₂m₁ + m₁c₂/ β ₂ +

×      + m1c1/ β1+µ2oβ1.

(c₂m₁ - c₁m₂)²

Она пропорциональна возмущению В _ч v³, квадратам 22 параметров инертности (m 2 ) и жесткости (c 2 ).

Решающим фактором снижения нагруженности здесь является исключение нуля знаменателя (19):

c1   m1/m2⋅ c2/3, c1≤900/3⋅1,1/1,72 130 кН/м. (20) Оптимальная диссипация в подвесе коника выявляется минимизацией дисперсии реакции:

D_r2 = min, ∂ D_r2/ ∂β ₁ = 0,      (21а)

в 1 □— J c mi , в 1 = 8,8 кНс/м. µ _o

В долях от критического значения β _кр = 2 с ₁ m ₁ она равна

ϑ=β 1 / β кр = 1/2 µ o = 0,3.      (21 б )

В долях от параметра   β 2 ≈ 0,2 с 2 m 2 =

= 7,8 кНс/м имеем:

в 1 □ 3 m 2 с 1 в₂(2Цо ^m ₂Г 1 = 5,8 кНс/м. (21 в )

Из сравнения (19) с учетом (20, 21) следует конкретная реакция шин КП для β 2 = 0,2 с 2 m 2 = = 7,8 кНс/м, m ₂ = 1720 кг:

Q = c 2 °_r □ m 2 -^B ч v ³ x

× c ₂/ β ₂ + c ₁/ β₁ = 11,7 m ₂ B _ч v ³.

Сопоставление этого решения с (13 б ) показывает близкие результаты одно- и двухступенчатого подвеса. Здесь во втором случае отразился гибкий подвес меньшей массы m 1 < m 2 . Сказалось также малое расхождение парциальных частот: с 2 / m 2 ≳ 3 c 1 / m 1 , ν 2 ≥ 3 ν ₁.

Примем в модели рис. 1 пачку хлыстов упругой с базисной функцией изгиба f(x) = sin πx / 2xc = = sin 3πx / 2lx. Введем координаты вращательного движения неизогнутой оси пачки z1 = z1 (1 – x / lx), Z1 = Zi(1 — X/lx) и относительного движения элемента dm — Цdx, Ц — mп / 1п на расстоянии X от подвеса с комлей. Тогда кинетическая энергия пачки и подрессоренных масс m2, КЗУ — mк и потенциальная сил упругости (Сп — С2, Cz — С1) будут равны:

l

2T = J (z+y )2 dm + m к z2 + m 2 z2, (23) В п mi = mi + m кз,

l

2 П = J EI ( x ) y "²( x ) dx + q( z i - z 2 )² + d

^{+ c} 2^{( z} 2 ^{- z} к^{) 2}.

Разлагая по Фурье у ( x , t ) = f ( x ) q ( t ) и вводя в (23), получим

2        -2                      .2

2T = mq + mizi + 2mпziq + m2z2, (24) 2 П = Cq 2 + ci( zi- z 2)2 + c 2 ( zi- z к ), ll где m =J f 2( x) dm, mi = J (1- x /1 )2 dm, d                  0

l mx = J (1-x /1) f (x) dm, 0 l c=J EI ( x ) f "2( x ) dx.

где m , m 1 , m _п — массы изгибных колебаний пачки, ее вращения ф — z i / 1 и инерционной связи двух движений ф , у ; С - эквивалентная жесткость изгибных колебаний пачки.

Вводя в интегралы (24) функцию изгиба пачки массой m п — 2400 кг, 1 _х — 1 3 + 1 4 — 6,8 + 10,2 — — 17 м и параметры 1 _о — П / 4 Г 4 ■ n , S _о = П Г 2 n , dm = р dV = р S _ocos²3 n x /2 1 _п, I ( x ) = I _о х X COS⁴ 3nx / 2 1 _п, получим эквивалентные массы и жесткости:

m = 0,37 m п = 880 кг, mi = m^ + m кз = 0,31 m п + 70 = 820 кг, (25) mи = 0,3 5mп = 820 кг, m2 — 1720 кг;

с — 28 EI о / 1 п = 150 кН/м, c 1 — 190, c 2 — 900 кН/м, P 2 — 0,2 ^с ₂ m ₂ = 7,8;

в — 0,12 4cm = 1,4 кНс/м.

Вводя квадратичные энергетические функции в уравнения Лагранжа (4) относительно координат q, xi — — zi - z2; z2 — x2 + zK, zi — xi + x2 + zк, получим mq+mH(xi + x2)+cq+P q=-mиZк

< m _H q+m^ + x 2 ) + c i x i +P i x i =- mz (26) ^ ^m2 x 2 ^{+ c} 2 ^x 2 ^+в 2 - x 2 ^- c i ^x i -P i - x i =^{- m} 2 ^Z к .

При Ci — TO, xi — 0; x2 — x, получим упрощенную систему с гибкой пачкой на шинном подвесе для m2 + mi — m^ — 2540 кг mq+P (q+cq+m и x=- m и zk

<                                                   (27 а )

m и q+m 2 x+P2 5c+c 2 x=- m 2 zk или, в операторно-матричной форме, -

^Л mp ^{2 +P} p + c     ^mи P ²     - m и P ^{2 z} K (P )

X m _H P ² m s P ^{2 +p} 2 P ^{+ c} 2 - m s P ^{2 z} K ( P ) у

. (27 б )

Определитель системы

А = [ ^m _д P ⁴ + P ^{3 ( p} 2 +Ц^{р )} + P ^{2 ( c} 2 +Ц С +

\28)

+ PP2 /m)+pc2(P+rP2)/m+cc2 /m]■ m, где mд = ms -mи /m = i776 кг, ц — ms / m — — 2,9; £ — с / с2 — 0,i7.

Частотное уравнение при р — i X , P i — 0 и частоты системы

4             2

А _о = m д Х - ( c 2 +Ц c ) X + cc 2 / m = 0,

• ^{2 m} А ^{Х 2} ,2 =

• - !----------₂----------------⁽²⁹⁾

= [( c 2 +Ц c ) + д/( c 2 +Ц c ) - 4 cc 2 m д / m .

Для исходных данных (25, 28) имеем: V — V с / m = — i7 с ^-1 ; V 2 — 7 c ₂/ m _s — 35,4 c ^-1 ; X 2, ₂ = — 142/610, X i — 11,9 с^-1, X 2 — 24,7 с^-1.

Получена амортизированная система при ограниченных параметрах диссипации в пачке и шинах: в = = 1,4; Р 2 = 7,8 кНс/м. Причем частоты Z 1 , Х 2 близки соответствующим частотам (16) квазиступен-чатого подвеса коника с жесткой пачкой. Однако во втором случае диссипация в конике (21 а ) ощутимо выше, чем в пачке (25).

Передаточная функция радиальной деформации шин по матрице (27 б ) и Крамеру

П X ( Р ) = x ( Р У z к ( Р ) =

^Д X ( Р ) = ^{д (} Р ) z к ( р )

=- Р 2 ms (ц Omp 2 +рР+cУ д( p X цп =1-m„ / my = 0,68; • О              и 4-i        '      '

в2 +Цв = 1,5в2, в + ^в2 = 2в, Р<<Р2.

Дисперсии деформации и реакции шин КП для спектра воздействия пути S к = D _и V ³ / to ⁴, Ц = m s / m = = 2,9; 8 = с / с 2 и параметров инертности системы (28, 25):

∞

D x = ~   I П x ( i ^to )l S к ( ^to ) d ^to =

2n J

-∞

∞ ∫ -∞

2 m = D ч v "^^х 2 n

2 2z- \4            z-..x2

ц ₀ m ( i to ) + 2 c ц ₀ m ( i to ) + c

I Д ( i to )|²

. 2

— d to ;

Параметры жесткости c и диссипации здесь практически неуправляемы, но теоретически могут быть вычислены минимизацией дисперсии реакции шин (30). Для исходных их значений (25) среднеквадратическое значение реакции равно:

ст _r = 7,75 m _s ^ B _ч v ³.          (31)

Этот результат совпадает с меньшим решением (13 б ) шинного подвеса с жесткой пачкой. В итоге гибкость пачки при одноступенчатом шинном подвесе не оказывает ощутимого влияния на вибронагруженность шин.

ВЫВОДЫ

Исследованы три структуры подрессоривания МТА с пачкой и получены одинаковые вибронагруженности МТА и пути (почвы). Это объясняется значительными ограничениями (20) на отношения жесткости шин и подвеса коника. Если они не реализуются, то остается лучшим по конструктивному исполнению одноступенчатый шинный подвес с минимально возможной жесткостью. Это достигается заменой обычных шин широкопрофильными с низким давлением.