Исследование полей собственных волн экранированного плоского волновода с двухслойным заполнением полупроводник-диэлектрик
Автор: Лобес М.В., Арефьев А.С.
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 4 т.7, 2009 года.
Бесплатный доступ
В линейном приближении получены диспер-сионные уравнения для определения постоянных распространения продольно-магнитных и продольно-электрических волн экранированного плоского волновода с двухслойным заполнением полупроводник-диэлектрик. Проведено исследование дисперсионных характеристик и распределений полей волн.
Короткий адрес: https://sciup.org/140191348
IDR: 140191348 | УДК: 621.372.8
Текст научной статьи Исследование полей собственных волн экранированного плоского волновода с двухслойным заполнением полупроводник-диэлектрик
Введение. Классификация собственных волн линии передачи
На рис. 1 изображено поперечное сечение плоского волновода с двухслойным заполнением полупроводник-диэлектрик (ПВДЗ ПД). Области 1 и 2, расположенные между двумя идеально проводящими плоскостями, представляют собой слои полупроводника и диэлектрика, соответственно. На основе данной волноведущей структуры могут быть построены различные СВЧ устройства, в частности, вентили [1-2], СВЧ модуляторы [3-4].
Рис. 1. Поперечное сечение ПВДЗ ПД
При формулировке краевой задачи в качестве исходных уравнений выберем уравнения Максвелла:
rot HH(m) = £(m) ^E-)+j(m), (m = 1;2), a at rot EE(m) = - д am) |H^-, (m = 1; 2 ), ot div EE(m) = p(m) / £aam), (m = 1; 2), div H(m) = 0, (m = 1; 2)
Здесь EE(m) и H(m) - напряженности элект рического и магнитного полей волны, распро- страняющейся в линии передачи, еam) и ^am) – абсолютные диэлектрическая и магнитная проницаемости среды, p(m) и j(m) - объемные плотности заряда и тока в среде, индекс m указывает номер области.
Будем считать, что полупроводник имеет элек-троннуюэлектропроводность;внемприсутствует только донорная примесь, концентрация которой Nд значительно превышает собственную концентрацию дырок pi . В данном случае можно пренебречь наличием дырок в полупроводнике. При этом в области 1 плотность заряда р(1) складывается из плотности заряда подвижных электронов проводимости рП1) и плотности заряда неподвижных донорных ионов рД1): р(1) = рП1) + рД1), а плот-~ ность тока в полупроводнике j() равна плотности тока электронов проводимости
1 ( 1 ) = -Ц n p n i ) EE ( 1 ) - D n grad Р ( 1 ) , (5)
где μ n и D n – подвижность и коэффициент диффузии электронов проводимости, соответственно. Величины μ n и D n связаны соотношением Эйнштейна D = кЛи / е, где kE - пос-
П Б П ' Б тоянная Больцмана, T – абсолютная температура полупроводника, e – абсолютное значение заряда электрона. Первое слагаемое в (5) задает плотность тока дрейфа, второе – плотность тока диффузии электронов проводимости. В диэлектрике плотности заряда и тока равны нулю р'2' = 0, j12' = 0.
Применим операцию дивергенции к уравнению Максвелла (1), записанному для полупроводника, принимая во внимание равенства (3), (5). В результате имеем:
2 О ( 1 )+ .En. о( 1 ) ( 1 ) + о( 1 )
D n V p n + (1) р n ( р и +р д ) + ε a
+ E п EE ( 1 ) grad рП1 ) —1^ = 0. ∂t
Будем считать, что донорная примесь равномерно распределена в полупроводнике. При этом плотность заряда донорных ионов Рд1) не зависит от координат grad рД1) = 0. (7)
Применение операции ротора к уравнениям Максвелла (1), (2) с учетом равенств (3)-(4) дает
-
o 2 ^( m ) ( m ) ( m ) d H
ε a μ a 2 ∂t
= u sradp(m )x E ( m )-n( m ) (m ) dH ( )
-
-
( m = 1; 2 ) .
Л 2 ? ( m ) ( m ) ( m ) d E
∂t
(
^*
-
( m ) d'-
∂ t dpnrl ∂ t
-
Представим плотность заряда электронов проводимости в полупроводнике р П 1 ) в виде суммы постоянной р П ) и переменной p^ V составляющих
О ( 1 ) = О(1 ) + о(1 ) r n р п 0 + p n , v *
Отсутствие дырок в полупроводнике означает, что в нем не происходит генерация электронно-дырочных пар. Как следствие, единственным механизмом возникновения электронов проводимости остается ионизация донорных атомов. В данном случае постоянная составляющая р ^о величины р П 1 ) равна по модулю плотности заряда донорных ионов
рП10 = -рД1). (11)
Наличие переменной составляющей p^V обусловлено воздействием на электронную плазму полупроводника со стороны поля волны, распространяющейся в направляющей структуре. В дальнейшем мы будем предполагать, что напряженности электрического и магнитного полей волны E ( т ) и H ( т ) , ( т = 1; 2 ) малы по абсолютному значению. При этом переменная и постоянная составляющие плотности заряда электронов проводимости в полупроводнике удовлетворяют условию (pnil <<|p$ |-
Будем считать, что величины 6 ( т ) , H ( т ) , и не зависят от поперечной координаты x . Подставляя (10) в (1)-(4) и пренебрегая в (1) слагаемым второго порядка малости (- p n p^ v EE ( 1 ) ) , можно заметить, что система из восьми скалярных дифференциальных уравнений, получаемая из урав-
нений Максвелла (1)-(4), распадается на две независимые системы.
Первая из них включает в себя в качестве неизвестных функций величины p^ v , H Xm^ , E Ут ) , E Zm ) , ( m = 1; 2 ) . Она соответствует продольномагнитным волнам или LM -волнам линии передачи. Для волн данного типа характерно отсутствие перпендикулярной к границе раздела полупроводник-диэлектрик составляющей напряженности магнитного поля H Ут ) , ( т = 1; 2 ) . Вторая система дифференциальных уравнений содержит компоненты E^ m ) , H ( m ) , H Zm ) , ( m = 1; 2 ) напряженностей и соответствует продольно-электрическим волнам или LE -волнам ПВДЗ ПД. Определением продольно-электрических волн может служить условие E ( m ) = 0 , ( m = 1; 2 ).. Очевидно, что в данном случае LM -волны можно также классифицировать как электрические или E -волны ( h Z ( m ) = 0, E Z ( m ) ^ 0 ) , ( m = 1; 2 ) ; LE -волны од-но-временно являются магнитными волнами или H -волнами ( e Z ( m ) = 0, H Zm ) ^^ 0 ) , ( m = 1; 2 ) .
Отсутствие у LE -волн переменной составляющей плотности заряда электронов проводимости p^ V означает, что эти волны не возмущают электронную плазму полупроводника. Данный факт объясняется тем, что в случае LE -волны единственная отличная от нуля компонента плотности тока в полупроводнике j X ) не зависит от координаты x , вдоль оси которой движутся электроны проводимости. Тем самым, в полупроводнике не образуются сгустки и разрежения подвижных носителей заряда. Иными словами, под действием электрического поля LE -волны все электроны проводимости в области 1 смещаются синхронно.
Вывод дисперсионных уравнений
Рассмотрим продольно-магнитные волны. В соответствии с условиями (11) и (7), постоянная составляющая плотности заряда электронов проводимости в полупроводнике р ^ о ) не зависит от координат
Подставим (10) в уравнение (6). Пренеб-
регая слагаемыми второго порядка малости p n ( P ( n 1,l ) 2 / е» ) , P n EE ( 1 ) grad P ( n ‘, V и учитывая соотношения (11)-(12), имеем
D n
< а2Р (1)
⎜ ρ n,v
∂y 2
∂z 2
, ^ n n( 1 )n( 1 )
+ ( 1 ) p n0 p n,v
-
др(1) ρn,v
= 0. (13)
После аналогичных преобразований векторное равенство (8), записанное в проекции на ось x, дает уравнение d2 H xm' d2 H xm'
dy 2 + dz 2
^^^^^^^е
' ,.' s 2 h ;-1 e a М a 8t1
^^^^^^^s
( m '
М am ^ n Р 2,, ( m = 1;2 ) Ot
Принимая во внимание линейность дифференциальных уравнений (13)-(14), будем предполагать, что искомое поле представляет собой гармоническую волну, распространяющуюся в направлении оси z . Воспользовавшись методом комплексных амплитуд, представим неизвестные функции p^ V , EE (m) , H ( m ) , ( m = 1; 2 ) как действительные части произведений комплексных функций ~П^ , EE (m) , H ( m ) , ( m = 1; 2 ) и фазового множителя exp [ i ( tot - y z ) ] . Здесь i - мнимая единица, ω – круговая частота колебаний, γ – неизвестная постоянная распространения волны.
Подставляя в (13) и (14) вместо величин p^ v и H Xm ) , ( m = 1; 2 ) соответствующие комплексные функции, получаем следующие дифференциальные уравнения
2~(1) d^ w = 0, dy d2 ~(m)
+ (5(m))2 H(m) = 0, (m = 1; 2), dy где введены обозначения:
⎛⎞ e=.o-^ p-10 - ”-y 2 • n ⎝εa
^m) = v ® 2^ am 1 ^ am 1 - y 2 + imp am p . p nm ,
( m = 1; 2 ) .
Решения уравнений (15) и (16) имеют вид:
~У ( У ) = A p cos ( R y ) + B p sin^y ) (19)
HH xm ) ( y ) = A HH ) cos ( j ( m ) y ) + B Hm ) sin ( j ( m ) y ) ,
( m = 1;2 ) , (20)
где Ap, Bp, AHm), BHm), (m = 1; 2) - неопределенные постоянные. Из уравнения Максвелла (1) могут быть получены следующие равенства позволяющие выразить компоненты напряженности электрического поля LM-волны.
Будем предполагать, что переход металл-по-лупроводник в плоскости y = 0 не обладает выпрямляющими свойствами, представляя собой омический контакт. На нем выполняется граничное условие
E? ( 0 ) = 0, (21)
соответствующее отсутствию поверхностного заряда на границе раздела металл-полупровод-ник [5]. Кроме того, на поверхности идеальных проводников обращаются в ноль тангенциальные составляющие напряженности электрического поля волны
E Z1 )( 0 ) = 0, e Z2 ) ( У 2 ) = 0. (22)
Граничные условия (21)-(22) позволяют сократить (с шести до трех) количество неопределенных постоянных в равенствах (19), (20) и в выражениях для компонент El ^ 1 ) , Е^й ) , (m = 1; 2 ) .
Условия непрерывности тангенциальных составляющих напряженностей электрического и магнитного полей волны и перпендикулярной составляющей электрической индукции на границе раздела полупроводник-диэлектрик в плоскости y= y 1 :
H X11 (У1)- H x2) (yi) = 0, sa1 E?l(y,)-sa2^! (У1) = 0,
E'XУ1)- E?' (У1) = 0
приводят к однородной системе линейных алгебраических уравнений относительно неопределен- ных постоянных, присутствующих в представлениях неизвестных функций (19)-(20). Условие совместности данной системы дает дисперсион- ное уравнение для определения постоянных распространения LM-волн ПВДЗ ПД ^ay 5(2) (z — i) e cos(5(1)У1 )sin(Ry!)+4y X £а' LY 8(1)
x sin ( 5 ( 1 ) y i ) cos ( ey i ) sin [ 8 ( 2 ) ( y 2 — y i ) ]
y ( Z + i ) [ cos ( 8 ( 1 ) y 1 ) cos ( py 1 ) - 1
~ (m) -
Ey =
E ~ ( m ) =
(m^-ito£(m )
μ n ρ n 0 i ωε a
iYHlm)
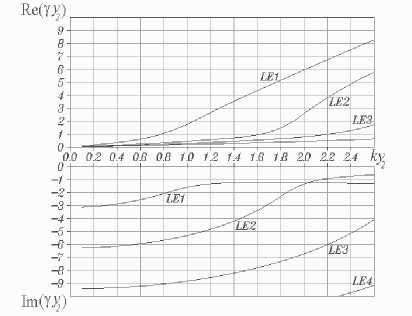
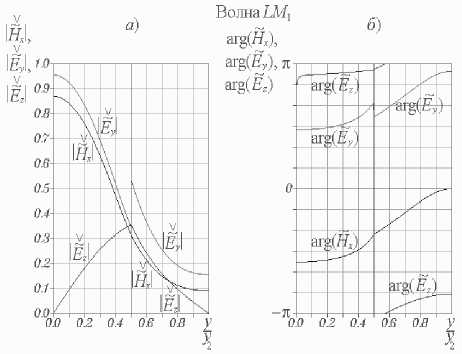
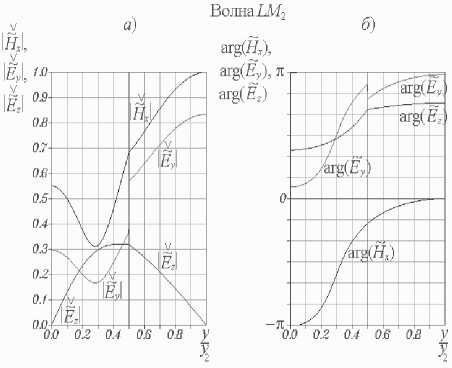
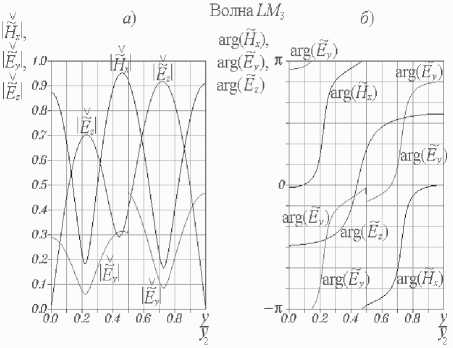
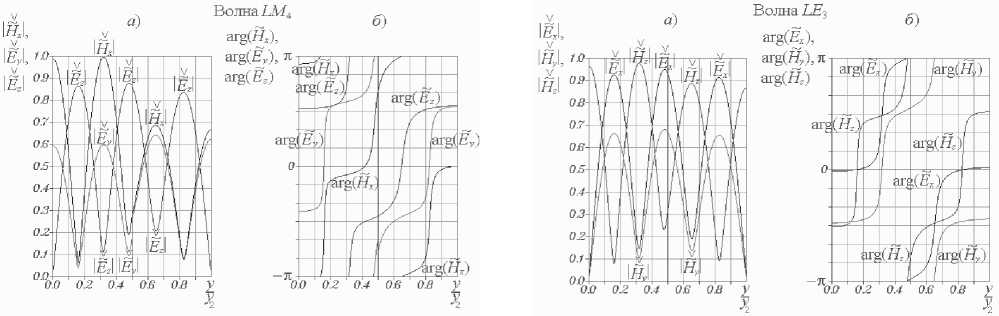
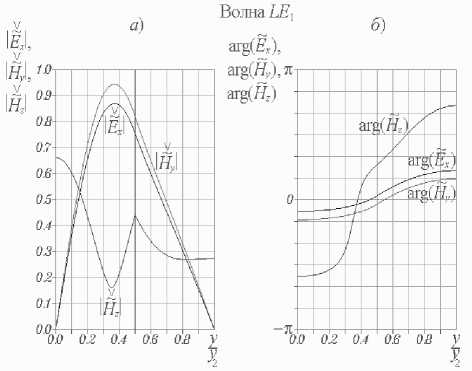
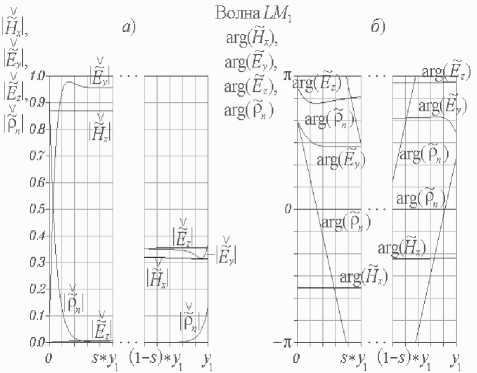
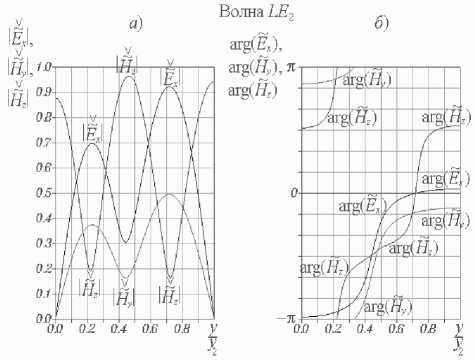
⎝r dHH м n pnm) - itoEam) I d>2 (m = 1;2), - D n ^ dy ⎠ + iA, i~nm ⎠ - ( v3 B8(1)) ⎜ γ ζ+iβδ ⎟ (PS(1)Y J sin (8(1)yi )sin(eyi) x cos[s(2)(У2 - yi)] = 0, ⎬× где введено обозначение Z = pпрП1с>/(®sа))• При этом координатные зависимости искомых величин имеют следующий вид: ~ ----YCH Гcos[8(2)(y2 - yt )]х DnW (У1, У1) L J х< i8(1) cos[e(yi - y)]+z Y-sin(5(1)yi)х х sin(e_y)- 8(i) cos(s(i)yi )cos(e,y) , H~x1)(y)=W C y)cos[8(2) (У2 - yi)]х х W(y, yi)- izY2 sin[8(1) (yi - y)]}, HHX2)(y) = Ch cos[8(2) (y2-y)], ~C Ey(y) w(yi, yi) иnp(io - х cos[s(2)(y2 - yi )]{-в8(i) sin[e(yi - y)] + + iZW(yi, y) + W(y, yi) - - iY2Z sm[5(i)(yi - y)]}, E2)(y) = -CH ~^р cos[8(2)(y2-y)] ms a) ~(i)(i;) = CH cos[8(2)(y^-yi)] x W(yi, yi) И прПс. - /гое ai) х {i'Zy28(i)cos[8(i)(yi - y)]- -Y28(i)cos[e(yi-y)] + iζγ2 — sin (8(i)yi )sin(Py) - 8(i)х × cos ;(8(i)yi )cos(e,y) + 8(i) [y2 cos(ey )х х cos(8(i) y)- в8(i) sin^y )sin (8(i) y)]}, Ez(2)(y) = CH -i^sin[8(2)(y2 - y)]. roSa) Д Ch = A^ /cos(s(2)У2), W (s1, s2) = P8(1)cos(s (1)s1 )sin(ps2)+ + у2sin(8(1)s1 )cos(ps2). В случае продольно-электрических волн можно ограничиться решением одного дифференциального уравнения. Подставляя (10) в уравнение (9), записанное в проекции на ось x, и отбрасывая слагаемые второго порядка малости, имеем d2 E Xm) d2 E xm) ∂y2 + ∂z2 - 2 (m) (m) (m) d Ex εaμa ∂t2 - (m) (m)dEx / _ 1 Ha Hnpn0 , (m= 1,2) ■ ∂t Уравнение (28), записанное относительно комплексной функции EX(m), (m = 1; 2), имеет следующий вид 2 ~(m) + (^(m))2 E~jm)= 0, (m = 1;2). (29) dy x Решение уравнения (29) E~xm)(y) = aE) cos(j(m)y) + BEm) sin(^(m)y), (m = 1; 2) содержит неопределенные постоянные A^), bE), (m = 1; 2). Используя граничные условия на металле E~X1)(0) = 0, E~X2) (У2) = 0, (30) получаем E^ (y) = BE1) sin (S(1)y), EX2)(y) = CE sin[8(2)(У2 - У)], где CE = -BE2 / cos(s(2)y2). Соотношения ~ (m) ~(m) _ Y~(m) ~(m) _ ~ i dE x H y Ex , H z y rnp am) юр vm) dy (m = 1; 2), следующие из уравнения Максвелла (2),позволяют найти компоненты напряженности магнитного поля LE-волны.Дисперсионноеуравнение дляопределения постоянных распространения LE-волн ПВДЗ ПД cos(S(1)У1) sin[S(2)(y2 - У1)] + to^®S^ sin(8(1)yi)cos[8(2)(У2 -yi)] + 8(1) ro^a2) получается из условий непрерывности компонент Ex , Hz напряженностей на границе раздела полупроводник-диэлектрик EX11 (yi)- EX2) (.yi)=0, й Z' (У1)- HH X2) (У1)- 0. При этом координатные зависимости компонент напряженностей LE-волн принимают следующий вид E^X1) (y) = CE z sin (s(1)y), E~X2)(y) = CEsin[8(2)(У2 - y)], HHУ1)(y) = Ce sin(8(1)y), ®pa) HHУ2)(y) = CE sin[8(2)(y2 - y)], ro^a) HHZ1)(y) =-Ce i8-^ cos(8(1)y), ro^a) HHZ2) (y ) = CE i8"^ COs[8(2) (y2-y)], ro^a) Анализ численных результатов При выполнении расчетов числовые значения параметров краевой задачи были выбраны следующим образом:расстояние между экранирующими металлическими пластинами y2= 2 -10 4 м; толщина слоя полупроводника у1 = 0,5 • у2; температура полупроводника T = 300 К; концентрация донорной примеси в полупроводнике Nд = 1021м-3; (рП1с>= -eNд); подвижность электронов проводимости в полупроводнике рn= 0,85 м2/(В -С); относительные диэлектрическая и магнитная проницаемости полупроводника е(1)= 13,1, р(1)= 1 (материал полупроводника – арсенид галлия); проницаемости диэлектрика е(2)= 9,05 , р(2)= 1 (материал диэлектрика – ГБ-7). На рис.2-3 изображены дисперсионные характеристики LM- и LE-волн ПВДЗ ПД. Здесь к = го / c – волновое число свободного пространства, c – скорость света в вакууме.Как следует из графиков,при k > 0 все собственные волны линиипередачиявляют-ся комплексными,действительные и мнимые части их постоянных распространения отличны от нуля.Пара-метры Re(Y) и Im(y) любой волны различаются по знаку.Этотфакт свидетельствует о том,что амплитуды компонент напряженностей убывают в направлении распространения волн.Условия дляусиления в данной направляющей структуре отсутствуют. Назовем волну квазираспространяющейся, если в ее постоянной распространения γ действительная часть преобладает над мнимой Под квазизатухающей будем понимать волну, постоянная распространения которой удовлетворяет условию Частоту ωкр, на которой действительная и мнимая части параметра γ равны по модулю, назовем критической частотой волны. Рис.2.Дисперсионные характеристики LM-волн ПВДЗ ПД Рис. 3. Дисперсионные характеристики LE-волн ПВДЗ ПД Очевидно, что определения (35)-(36) квази-распространяющихся и квазизатухающих волн можно также записать в виде - — < arg(y) < 0 и ππ - 2 < aw) <--• Индексацию LM- и LE-волн ПВДЗ ПД будем производить в порядке увеличения их критических частот. Нормированные значения критических волновых чисел ккр= гокр/ c некоторых волн приведены в таблице 1. Таблица 1. Тип волны LM1 LM2 LM3 LE1 LE2 kкр y2 0 0,92 1,89 0,97 1,88 На основании рис. 2-3 можно сделать следующие выводы. Волна LM является квазирас-пространяющейся на любой частоте го > 0. Остальные LM- и LE-волны ПВДЗ ПД в частотных диапазонах (0 < го < гокр) и (го > гокр) следует квалифицировать, соответственно, как квазизатухающие и квазираспространяющиеся. Действительные части постоянных распространения всех волн возрастают с увеличением частоты. Мнимые части постоянных распространения всех волн, за исключением волны LM , возрастают с увеличением числа k от нуля. На некоторых частотах, превышающих критические, параметры Im(y) достигают максимальных (минимальных по модулю) значений, вновь убывая при дальнейшем увеличении k. Например, максимальные значения мнимых частей постоянных распространения волн LE1 и LM2 достигаются, соответственно, при ky2 = 1,66 и ky2 = 2,49. Определим предельные значения постоянных распространения волн при неограниченном уменьшении частоты. Умножая уравнение (32) на го и полагая го = 0, получаем: Н ^ Y = 0. y н a2) В случае равенства магнитных проницаемос-тей полупроводника и диэлектрика Н ^ = Н(2) = На (39) это уравнение принимает вид sh(Y.y2)/(рaY) = 0-Отсюда Рис. 4. Распределения амплитуд (а) и фаз (б) компонент напряженностей поля волны LM : ky2 = 2 ; верхней точке оси ординат на рис. а соответствуют ∨∨ ∨ значения: H~x = 11, E~y = 2,5, E~z =2,5 Знаки «–» и «+» в равенстве (40) соответс-твуютпредельным значениям постоянныхрас-пространения LE-волн, распространяющихся, соответственно,в направлении оси z и в противоположном направлении. Корни уравнения (32) будут также определяться равенством (40) в случае, если условие тождественности магнитных проницаемостей полупроводника и диэлектрика (39) заменить требованием идентичности размеров частичных областей 1 и 2 на рис. 1 y1 = y2 - у1 или уг = 2y1. Рис. 3 позволяет убедиться в справедливости соотношения (40). Что касается LM-волн, то для них предельное соотношение, аналогичное (40), не выполняется,хотя на основании рис.2и может возникнуть такая иллюзия. Уравнение (26) позволяет лишь доказать аналитически, что при ω → 0 постоянная распространения γ волны LM неограниченно уменьшается по модулю. На рис. 4-10 изображены распределения амплитуд и фаз нормированных компонент напряженностей электрических и магнитных полей семи волн ПВДЗ ПД. В случае LM-волн безраз-V V мерные функции H , E и ρ~ n введены следующим образом: ∨∨ — — — — H = H / CH , E = E д/80 / ^0 / CH , рn = pncy2 I CH . Нормировочные соотношения для LE-волн имеют вид: ∨∨^* ^* ^* ^* Рис. 5. Распределения амплитуд (а) и фаз (б) компонент напряженностей поля волны LM2: ky2= 2 ; верхней точке оси ординат на рис. а соответствуют значения: H~x=1, E~y= 0,38, E~z= 0,38 Рис. 6. Распределения амплитуд (а) и фаз (б) компонент напряженностей поля волны LM3: ky2 = 2 ; верхней точке оси ординат на рис. а соответствуют ∨∨ ∨ значения: Hx = 1,1, Ey = 0,35, Ez = 0,35 Рис. 7. Распределения амплитуд (а) и фаз (б) компонент напряженностей поля волны LM4: ky2 = 2 ; верхней точке оси ординат на рис. а соответствуют ∨∨∨ значения: Hx = 1,5, Ey = 0,6, Ez =0,6 Рис. 8. Распределения амплитуд (а) и фаз (б) компонент напряженностей поля волны LE1: ky2= 2 ; верхней точке оси ординат на рис. а соответствуют ∨ ∨∨ значения: E~x = 2,5, H~y =7, H~z =7 Рис. 10. Распределения амплитуд (а) и фаз (б) компонент напряженностей поля волны LE3: ky2 = 2 ; верхней точке оси ординат на рис. а соответствуют ∨∨∨ значения: Ex = 1,1, Hy = 5,2, Hz = 5,2 Рис. 9. Распределения амплитуд (а) и фаз (б) компонент напряженностей поля волны LE2: ky2 = 2 ; верхней точке оси ординат на рис. а соответствуют ∨ ∨∨ значения: E~x = 1,1, H~y = 3, H~z =3 Рис. 11. Распределения амплитуд (а) и фаз (б) компонент напряженностей поля волны LM1 вблизи границ слоя полупроводника: ky2= 2 ; s = 0,01 ; верхней точке оси ординат на рис. а соответствуют значения: ~∨ ~∨ ∨ ∨ IHx| = 11, |ey| = 2,5, |E~z| = 2,5, |~n| = 8.104. Компоненты напряженностей должны удовлетворять граничным условиям (22), (30) на поверхности идеальных проводников, условиям (23)-(25), (33)-(34) на границе раздела полупроводник-диэлектрик, включая условие непрерывности перпендикулярной составляющей магнитной индукции н № !"CУ1)-t^H. !2|CУ1)=0, а также граничному условию на омическом контакте (21). Выполнение всех перечисленных условий, за исключением (21) и (24), с очевидностью следует из рис. 4-10. Чтобы снять все сомнения относительно компоненты Ey , следует построить аналогичные распределения компонент напряженностей вблизи границ полупро- водникового слоя (см. рис. 11). Приведенные на рис. 1 1а графики, позволяют убедиться в том, что компонента Ey волны LM1 удовлетворяет условию (21). Кроме того, из рис. 4б и 11б следует непрерывность фазы компоненты Ey на границе раздела полупроводник-диэлектрик благодаря чему обеспечивается выполнение граничного условия (24). Можно заметить, что, в большинстве случаев, фазы компонент напряженностей полей LM- и LE-волн возрастают в направлении оси y . Однако есть и исключения из данного правила. Прежде всего, это компоненты Ey LM-волн, аргументы которых немонотонны в слое полупроводника вблизи границы его раздела с диэлектриком. Наиболее наглядно подобную немонотонность иллюстрирует рис. 11б. Кроме того, например, при числовых значениях параметров краевой задачи, соответствующих рис. 7, функция arg[E~z(1)(y)] волны LM4 достигает минимума в точке у / у2 = 0,026. Обращает на себя внимание тот факт, что в окрестностях точек, в которых амплитуды компонент напряженностей достигают минимальных значений, фазы соответствующих компонент быстро изменяются с увеличением координаты y. Например, фазы компонент Hx и Ey напряженностей поля волны LM3 (рис. 6) проявляют значительную координатную зависимость в точках y / y2 = 0,22 и y / y2 = 0,73, соответствую- щих минимальным значениям амплитуд этих компонент. Максимальное значение функции d / dy{arg[ez (y)]} и минимальное значение функ- ции |Ez (у) достигаются в точке у / у 2 = 0,44. Данную закономерность легко обосновать. Если бы область 1 на рис. 1, вместо полупроводника, была заполнена идеальным диэлектриком, то в некоторых продольных сечениях линии передачи y = y0 амплитуды компонент напряженностей тех или иных волн не просто достигали бы минимальных значений, а обращались бы в ноль. По обе стороны от указанных сечений (в точках y = y0 - Ay и У = У0 + Ay) соответствующие компоненты напряженностей совершали бы колебания в противофазе. Иными словами, фазы данных компонент испытывали бы разрывы в точках y = y0 . Причем левый и правый односторонние пределы фаз в этих точках различались бы на 180о. В нашем случае направляющая структура частично заполнена средой с потерями. Поэтому, вместо нулей амплитуд компонент напряженностей, мы имеем их минимумы; вместо точек разрыва фаз, имеем точки, в которых фазы существенно зависят от координаты y . Напряженность магнитного поля любой LM-волны имеет единственную компоненту Hx. Тем самым, магнитные поля LM-волн ПВДЗ ПД линейно поляризованы. Аналогичным свойством обладают электрические поля LE-волн, векторы E которых ориентированы параллельно оси x. Очевидно, что электрическое поле LM-волны будет линейно поляризовано в тех точках, в которых фазы компонент Eyи Ezего напряженности будут удовлетворять условию arg [E y (y )]-arg \tz (y )] = ±nn, (n = 0;l_). Иначе поляризация электрического поля волны будет эллиптической. В последнем случае вектор E будет вращаться по часовой стрелке, если смотреть в направлении оси x, при условии: и против часовой стрелки при условии: Как следует из рис. 4б и 11б, при выбранных числовых значениях параметров краевой задачи электрическое поле волны LM эллиптически поляризовано в любой точке. В соответствии с рис. 5, электрическое поле волны LM2 линейно поляризовано в точке y / y2= 0,29, в которой В этой точке угол наклона напряженности E относительно оси z имеет два возможных значения: arctg|E~y(y)/ E~z(y) = 29,64° и На интервалах (y < 0,29) и (y > 0,29) за период колебаний конец вектора E описывает эллипс в плоскости (y, z), вращаясь,соответственно,против часовой стрелки и по часовой стрелке, если смотреть в направлении оси x. Электрическое поле волны LM3 (см. рис. 6б) линейно поляризовано в трех точках: y / y2 = 0,24 , y I y2 = 0,42 , y I y2 = 0,746 . В этих плоскостях положительные углы наклона вектора E относительно оси z составляют, соответственно, 5,848о, 44,65о, 6,25о. Сведения о поляризации магнитных полей LE-волн ПВДЗ ПД со- держатся в таблице 2. При этом числовые значения параметров линии передачи и частота колебаний соответствуют рис. 8-10. Таблица 2. Тип волны Точки линейной поляризации маг нитного поля y/y2 Положительный угол наклона напряженно сти H относительно оси z LE1 0,36 80,10о LE2 0,22 62,71о 0,48 11,27о 0,70 67,23о LE3 0,12 58,98о На основании рис. 8-10 можно сделать вывод о том, что сдвиг фаз между компонентами Ex и H y напряженностей поля любой LE-волны не зависит от координаты y и удовлетворяет условию 0 < {arg[E~x(У)]-arglHHy (y)]}<2 Действительно, исходя из второго уравнения Максвелла, можно получить следующее соотношение, свя- зывающее комплексные амплитуды этих компонент (m = 1; 2). Тем самым, в обеих частичных областях (рис. 1) аргументы комплексных чисел Hyи Exудовлетворяют условию В соответствии с определением (37), формула (41) дает условие 0 < {arg[E~x(У)]" arg[HHу(У)]}< 4 выполняющееся для квазираспространяющихся продольно-электрических волн. При ky2= 2 таковыми являются волны LE1 и LE2 (см. рис. 8-9). Используя определения (38), для квази-затухающих LE-волн получаем П < {arg[E~x (у )]" arg\.Hу (у )]}< 2- Последние неравенства справедливы для волны LE3 (см. рис. 10). Первое уравнение Максвелла, записанное для слоя диэлектрика, дает - yHX2)= tos^EE^V Тем самым, в частичной области 2 (см. рис. 1) сдвиг фаз между компонентами Eyи Hxнапряженностей LM-волн не зависит от координаты y и определяется соотношением Отсюда, аргументы комплексных функций ~ (2) ~ (2) Eу ) и Hу квазираспространяющихся и квазизатухающих LM-волн должны удовлетворять условиям 3П < {arg[^2)(у)]- arg[HHХ2)(у)]}< К (42) и П < (argЙ2)(у)1- arglHHХ2)(у)]}< 3П, (43) соответственно. При ky2= 2 неравенствам (42) удовлетворяют волны LM , LM2, LM3 (см. рис. 4б, 5б, 6б), неравенствам (43) удовлетворяет волна LM4 (рис. 7б). В частичной области 1 (рис. 1) сдвиг фаз между компонентами Eyи Hxнапряженностей LM-волн зависит от координаты y. Это обусловлено тем, что в слое полупроводника протекает ток. При выбранных числовых значениях параметров линии передачи и нормированном волновом числе ky2= 2 мнимая часть параметра β , определяемого равенством (17), удовлетворяет условию Im(Py2) << —1, поскольку (^ )2+(г^2 )2 = kDyl (с-0= = -(2,13727 + 5,45716 i)-106 == 5,86076 -106 exp(- 0,61882 п i). В данном случае, уже при небольших значениях координаты y справедливы следующие приближенные представления: Аналогичным образом можно записать: cos[p(yi - y)]« 2 exp{i Re[p(yi - y)]}x Подстановка выражений (44)-(45) в (27) дает x exp{- Im[e(У1 - у)]}- - Z i—sin(8(1)У] )+8(1) cos(s( × Слагаемое в правой части (46), содержащее множитель exp[- Im(Py)], быстро возрастает с увеличением координаты y; слагаемое, содержащее множитель exp{- Im[p(у1 - у)]}, так же быстро убывает. В результате, при удалении точки наблюдения вглубь слоя полупроводника, комплексная амплитуда ρ~n быстро убывает по абсолютному значению, что иллюстрирует рис. 11 а. Вблизи этих границ функция ~n (у) описывается приближенными выражениями i — sin (s(1) уг )+8(1) β1 /s(i) cos(ov)У1 × которые следуют из (46). Тем самым любая LM-волна возмущает электронную плазму полупроводника только в очень тонких приповерхностных слоях. В таблицах 3-4 приведены нормированные значения координат yp1и ур2точек, в которых амплитуда переменной составляющей плотности заряда электронов проводимости I~n (У) на порядок меньше, чем на границах раздела полупроводник-металл и полупроводник-диэлектрик: Таблица 3. Нормированное волновое число ky 2= 2 Тип волны LM1 LM2 -ypy У2 0,00115143099194 0,00115143132163 Урл~ У2 0,00115143099215 0,00115143132188 Ур2 У2 0,49884856900806 0,49884856867837 у^ У2 0,4988485690078 0,49884856867812 Как следует из рис. 1 1б, на границе раздела металл-полупроводник совпадают фазы переменной составляющей плотности заряда электронов проводимости в полупроводнике p^V и перпендикулярной составляющей напряженности электрического поля E^1) волны LM1 агд[рП1) (°)]=:'rg[E~y" (0)]- (49) Таблица 4. Тип волны – LM1 ky2 0,1 1 ^р,1 У2 0,00157183437282 0,00137565645622 Ур1~ У2 0,00157183437312 0,00137565645594 Ур2 У2 0,49842816562718 0,49862434354378 Уд^ У2 0,49842816562688 0,49862434354406 Рп (0) Рп (Ур,1 Рп (У1) Рп (Ур,2. = 10. Значения величин ур1 и ур,2 вычислены с использованием формулы (27) для ~n (у). Кроме того, в таблицах 3 и 4 приведены приближенные значения УрД~ и УрЛ~ величин Урд и Ур,2 , определяемые равенствами полученными из (47)-(48). Как можно убедиться, значения величин УрД, УрД ~ и Ур^, УрЛ~ совпадают с точностью до 10-12 значащих цифр, соответственно. Результаты расчетов показывают, что данная закономерность справедлива и для других LM-волн линии передачи. Для обоснования указанного свойства запишем третье уравнение Максвелла для функций ET^1)(у), ЕТ9) (у) и ~П1)(у): ^Ef dy ~ (1) Представим входящие сюда комплексные величины следующим образом: В результате уравнение (50) принимает вид ~(1) ~(1) 1 |~(1) ~(1) Полагая y = 0 и используя условия (21)-(22) на границе раздела металл-полупроводник, получаем I ^E11(y) ⎝ dy ⎠ expi argE1) (0)]}= y=0 Приравнивая аргументы комплексных чисел, стоящих в левой и правой частях равенства, приходим к доказуемому фазовому соотношению (49).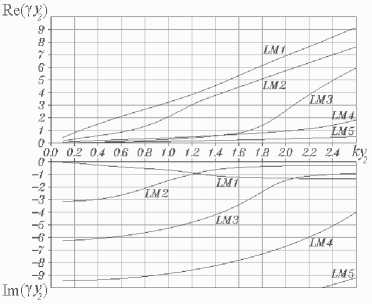
0 < {arg[E~y(У)]" arg[E~z(У)]}< n
- n < {arg[E~y (y)]- arg[E~z(y)]}< 0.
Список литературы Исследование полей собственных волн экранированного плоского волновода с двухслойным заполнением полупроводник-диэлектрик
- Кац Л.И., Попов В.В., Ревзин Р.М. К расчету невзаимных устройств для субмиллиметрового диапазона//Радиотехника и электроника. Т.22, №6, 1977. -С. 1107-1113.
- Захаров В.А. О медленных волнах плоскопараллельного волновода, заполненного двухслойной структурой диэлектрик -поперечно намагниченная полупроводниковая плазма//Радиотехника и электроника. Т.26, №4, 1981. -С. 673-682.
- Гусаков В.В., Кац Л.И. Модуляция миллиметрового излучения в МДП структуре//Журнал технической физики. Т.49, №6, 1979. -С. 13061309.
- Гусаков В.В., Кац Л.И. МДП-модулятор СВЧ-диапазона на основе пленок InSb//Радиотехника и электроника. Т.28, №8, 1983. -С. 1671-1673.
- Барыбин А.А. Волны в тонкопленочных полупроводниковых структурах с горячими электронами. М.: Наука, 1986. -288 с.


