Исследование поверхностной структуры твердых тел и жидкостей методом эллипсометрии с учетом математической некорректности обратной задачи. 5. О реальных возможностях метода последовательных приближений в решении обратной задачи

ВВЕДЕНИЕ. ПОСТАНОВКА ЗАДАЧИ

В работах [1–4] для решения математически некорректной обратной задачи эллипсометрии предложен метод последовательных приближений. Данный метод демонстрирует надежность и хорошие возможности при исследовании отражающих систем типа "полупроводниковая под-ложка—прозрачная сверхтонкая пленка". При этом речь идет об определении всех 4 параметров таких систем. Однако метод последовательных приближений не является окончательно завершенным. Его необходимо привести к более простому и удобному для практических применений виду. Для более четкой постановки задачи кратко остановимся на основных моментах метода.

Метод последовательных приближений выдвигает определенные требования к выбору начальных значений n0(0) , κ0(0) оптических постоянных подложки для каждого шага этого метода. При этом особое внимание должно быть уделено выбору начальных значений n0(0) , κ0(0) для первого шага метода. Фиксируя эти начальные значения, мы определяем параметры d и n пленки в точке абсолютного минимума функционала обратной задачи S0 , а на траектории, ведущей к точке абсолютного минимума, путем использования соответствующих правил отбора (cм. [1]) устанавливаем первичные оптимальные значения параметров пленки. Этот вопрос подробно обсуждается в работах [3–5], но ввиду его важности к нему необхо- димо снова вернуться. Сформулированные в работе [3] правила выбора начальных значений для первого шага имеют следующий смысл. Начальное значение n0(0) должно обеспечивать для показателя преломления n пленки в точке абсолютного минимума функционала обратной задачи S0 выполнение условия nmin ^ 1, или nmin = 1 + а , а « 1.      (1)

Что касается параметра κ ₀ ⁽⁰⁾ , то для него при таком подходе к выбору начальных значений оптических постоянных подложки целесообразно остановиться на нулевом значении

^ 00) = 0.                          (2)

Определенные таким образом начальные значения n ₀ ⁽⁰⁾ , κ ₀ ⁽⁰⁾ не зависят явным образом от типа экспериментальных ошибок и вследствие этого не дают четкого представления о выраженности математической некорректности обратной задачи. В принципе, можно добиться, чтобы величина n ₀ ⁽⁰⁾ достаточно слабо отличалась от точного значения показателя n ₀ , однако данный факт сам по себе особого интереса не представляет. Важен только процесс по сближению точек

( d _min , n _min ) и ( d_opt , n_opt ),             (3)

из которых первая представлена параметрами пленки в точке абсолютного минимума функционала S0 , а вторая — оптимальными значениями данных параметров. Очевидно, обеим точкам соответствуют одни и те же фиксированные значения параметров n0(0) , κ0(0) . Таким образом, выбор начальных значений n0(0) , κ0(0) носит относительный характер. Здесь важно лишь, чтобы на первом шаге при любом типе экспериментальных ошибок обязательно выполнялось условие nmin < nopt . (4)

Что касается условия n00) < (n0)true , где (n ) — точное значение показателя пре-0 true ломления n0 , то при таком подходе к выбору начального значения n0(0) данное условие, вполне соответствующее условию (1), не является обязательным, точнее, оно может и не выполняться. По поводу начального значения κ0(0) отметим только, что, начиная с некоторого шага метода, необходимо рассматривать последовательность значений κ0(0) из некоторого интервала. А до этого, последовательно увеличивая параметр n0(0) , для величины κ0(0) можно использовать наравне с другими значение (2).

В работе [5] предложен другой способ определения (для первого шага) начальных значений n0(0) и κ0(0) оптических параметров подложки по точке абсолютного минимума функционала S0 , определенной в пространстве всех четырех параметров однослойной отражающей системы d , n , n0 , κ0 . (5)

В связи с отмеченной выше ролью начального значения n ₀ ⁽⁰⁾ этот способ не имеет особых преимуществ, и от него следует отказаться. В то же время процедура по определению точки абсолютного минимума функционала обратной задачи S ₀ играет очень важную роль в другом плане. По точке абсолютного минимума устанавливаются типы экспериментальных ошибок, а также определяется степень выраженности математической некорректности обратной задачи в зависимости от величины и типа экспериментальных ошибок.

При использовании метода последовательных приближений наиболее простая ситуация возникает, когда коэффициент поглощения подложки считается известным. Если же этот коэффициент также подлежит определению, задача значительно усложняется. Для этого общего случая в работе [4]

предложена дополнительная процедура, обеспечивающая выбор однозначного решения. Речь идет о процедуре, направляющей процесс сходимости к оптимальным значениям параметров, наиболее приближенным к их точным значениям. Смысл данной процедуры сводится к следующему.

Основную роль в перемещении точки минимума ( d _min , n _min ) играет показатель n ₀ , т. е. его изменение вдоль некоторой возрастающей последовательности начальных значений показателя преломления подложки

{ n 0 ⁽⁰⁾ }. (6)

Вследствие этого переход точки минимума ( d _min , n _min ) через точку оптимальных значений ( d_opt , n_opt ) наблюдается при любой величине κ ₀ ⁽⁰⁾ , определенной на последовательности физически разумных значений этой величины

{ κ 0 ⁽⁰⁾ }. (7)

Задача состоит в том, чтобы из множества переходов точки минимума ( d _min , n _min ) через точку оптимальных значений ( d_opt , n_opt ) выбрать тот переход, которому соответствует оптимальное решение, наиболее приближенное к точному решению обратной задачи. И поскольку каждому такому переходу соответствует определенное значение κ ₀ ⁽⁰⁾ , то правильный выбор перехода означает и выбор величины κ ₀ как одного из параметров решения обратной задачи. Установление совокупности переходов точки минимума ( d _min , n _min ) через точку оптимальных значений ( d_opt , n_opt ) , отвечающих набору параметров κ ₀ ⁽⁰⁾ из последовательности (7), принципиальных затруднений не представляет. Что касается выбора из этой совокупности перехода, которому отвечает оптимальное значение коэффициента κ ₀ , то это довольно сложная задача. В работе [4] для этой цели используется сравнительный анализ функций

• ^dopt = ^{f (} n 0 ), n opt = ^f 2 ⁽ n 0 ). ⁽⁸⁾

Поведение кривых, соответствующих функциям (8), определяется значениями параметра κ ₀ из последовательности (7). Для оптимального значения κ ₀ кривые (8) в пределах некоторого сравнительно небольшого интервала для параметра n ₀ с центром в точке перехода являются наиболее пологими. Иначе говоря, приращения функций (8) в пределах указанного интервала относительно его центра для оптимального значения κ ₀ минимальны.

Определив по данному признаку оптимальное значение κ ₀ , остальные параметры решения обратной задачи находим с помощью простых соотношений. В результате полное решение обратной задачи запишется:

^d ” d min » d opt ,   n » n min » n opt ,

(0)                         (0)

n 0 ~ n 0 ,          ^K 0 ~ ^K 0 ,

где величины d _min , d_opt , n _min , n_opt , n ₀ ⁽⁰⁾ , κ ₀ ⁽⁰⁾ соответствуют выбранному переходу. Однако описанная процедура по выявлению оптимального значения коэффициента поглощения подложки довольно трудоемка [4]. В этом случае для каждого параметра κ ₀ ⁽⁰⁾ из последовательности (7) приходится определять точку минимума и точку оптимальных значений, причем для набора значений n ₀ ⁽⁰⁾ из последовательности (6). Это обеспечивает определение функций (8) и момент перехода одной точки через другую. Кроме того, сам критерий отбора оптимального значения κ ₀ , основанный на изучении поведения функций (8), носит несколько размытый характер, а это может заметно снизить точность решения обратной задачи.

В связи с изложенными соображениями основной целью настоящей работы является максимальное упрощение метода последовательных приближений для решения обратной задачи для случая отражающей системы с прозрачной сверхтонкой пленкой. Данное упрощение касается как выбора начальных значений n ₀ ⁽⁰⁾ и κ ₀ ⁽⁰⁾ оптических параметров подложки, так и процедуры по определению оптимального значения коэффициента поглощения κ ₀ подложки. При этом для иллюстрации основных положений метода воспользуемся результатами численного эксперимента для той же модели отражающей системы, что и в работах [1–5]:

d = 2.50 нм, n = 1.50, n ₀ = 3.865, k ₀ = 0.023.

Длина световой волны определяется значением 1 = 632.8нм, а углы падения ф₀ светового пучка изменяются от 50 до 75 град с шагом 2.5º. В численном моделировании экспериментальных ошибок максимальные отклонения (в ту или другую сторону) поляризационных углов Т и А от их точных значений определяются величинами ξ ₀ и η ₀ .

Для начала рассмотрим наиболее простую ситуацию, когда коэффициент κ ₀ считается известным.

РЕШЕНИЕ ОБРАТНОЙ ЗАДАЧИ ДЛЯ ОДНОСЛОЙНОЙ ОТРАЖАЮЩЕЙ СИСТЕМЫ С ИЗВЕСТНЫМ КОЭФФИЦИЕНТОМ ПОГЛОЩЕНИЯ ПОДЛОЖКИ

Мы используем здесь основные положения методики, изложенной в работе [4], в то же время максимально упростим соответствующую процедуру. При этом упрощение будет обусловлено не только тем, что известен коэффициент поглощения подложки. Упрощенная процедура будет использована и для общего случая, когда определению подлежат все четыре параметра однослойной системы с прозрачной сверхтонкой пленкой.

Прежде всего остановимся на выборе начального значения n ₀ ⁽⁰⁾ показателя преломления подложки для первого шага метода. Использование для этой цели условия (1) является излишним. При выборе данного параметра важно только, чтобы при любом типе экспериментальных ошибок обязательно выполнялось условие (4), причем данное условие не должно быть столь сильным, как это следует из (1). В связи с отмеченным свойством условия (4) процесс выбора начального значения n ₀ ⁽⁰⁾ может быть значительно упрощен. Этот вопрос для случая сверхтонких пленок решается довольно просто. Необходимо принять для толщины пленки нулевое значение d = 0, а в этом случае показатель преломления n перестает играть какую-либо роль и найти решение для параметров n ₀ и κ ₀ . Найденный таким образом параметр n ₀ в отличие от коэффициента поглощения κ ₀ довольно слабо отличается от его точного значения. Для определенности воспользуемся результатами численного эксперимента для модели отражающей системы (10). Для рассмотренных в предыдущих работах четырех вариантов экспериментальных ошибок имеем:

^ о = П о = 1мин: n ₀ ~ 3.8535, к ₀ = 0.2044, ^₀ = п ₀ = 3 мин : n ₀ ~ 3.8540, к ₀ = 0.2049, ^₀ = п ₀ = 5 мин: n ₀ ~ 3.8527, к ₀ = 0.2028,

^ о = П ₀ = 10 мин : n ₀ ~ 3.8546, к ₀ = 0.2049.

Как видим из (11), параметр n0 в рассмотренном приближении действительно слабо отличается от его точного значения (10), в то время как коэффициент поглощения κ0 увеличивается на порядок. Однако значение коэффициента κ0 из выражений (11) интереса не представляет, данный коэффициент в настоящем разделе считается заданным, а в общем случае он определяется совершенно другим способом. Интерес представляют значения показателя n0 из выражений (11). Выберем значение n0 , например, для второго варианта из (11):

n 0 = 3.8540.                 (12)

Фиксируя для параметра n0 значение (12) и используя известную величину κ0 , определим затем для данной ситуации путем решения обратной задачи величины dmi n и nmi n , а также оптимальные значения параметров пленки dopt и nopt . Рассматриваемая процедура строится относительно показателей преломления n0 и n , поэтому толщина пленки нас пока не интересует. Если найденные величины nmi n и no p t не удовлетворяют условию (4) или же удовлетворяют данному условию, но разность этих величин слишком велика, то в этом случае значение (12) для величины n0 не может определять начальное значение n0(0) . Второй случай как раз и реализуется для величины n0 , определенной выражением (12). Однако для такой ситуации величина no p t может служить некоторым ориентиром. Учитывая такую роль первичной величины n , зададим для показателя пленки не-o p t которое граничное значение ng r , удовлетворяющее условию ngr < nopt .                       (13)

При этом разность величин ngr и nopt не должна быть слишком малой. Смысл этого требования станет понятным чуть ниже. Будем решать обратную задачу для случая фиксированных величин n0 и κ0 , введя ограничитель ng r для параметра n . Смысл данного ограничителя сводится к следующему. В математической программе, предназначенной для решения обратной задачи, предусмотрена процедура, согласно которой последовательность точек (d, n) , определяемая при некоторых фиксированных значениях n0 и κ0 , или обрывается, как только первый раз выполнится условие n > ngr ,                       (14)

или же естественным образом сходится к точке минимума, для которой nmin < ngr .                      (15)

В первом случае или величина nmi n , не определенная из-за обрыва последовательности, слишком близко приближается к значению no p t , удовлетворяя условию (4), или же при любой величине разности (nmin -nopt) условие (4) не выполняется. И то, и другое делают невозможным использование соответствующей величины n0 в качестве начального значения n0(0) . Во втором случае величина nmi n , удовлетворяющая неравенству (15), очевидно, обеспечивает в силу (13) выполнение условия (4). Но здесь еще необходимо, чтобы величины из неравенства (15) были достаточно близки nmin » ngr .                    (16)

Это означает, что соответствующая величина n ₀ , обеспечивающая выполнение соотношений (15) и (16), может быть принята за начальное значение n ₀ ⁽⁰⁾ . Выше отмечалось, что разность величин n_{g r} и n_{o p t} не должна быть слишком малой. Такое требование должно обеспечивать сохранение условия (4) для величин n _{mi n} и n_{o p t} , соответствующих установленному значению n ₀ ⁽⁰⁾ . Отметим также, что введение граничного значения n_{g r} призвано уменьшить трудоемкость вычислительного процесса, связанного с определением начального значения n ₀ ⁽⁰⁾ .

Фиксируя затем найденное начальное значение n0(0) и используя известную величину κ0 , определим для данной ситуации новую точку оптимальных значений (dopt, nopt) . При этом соответствующая точка минимума (dmin, nmin) находится повторно. Новое оптимальное значение no p t в общем случае не совпадает с первичным значением этого параметра. Поэтому условие (4) должно быть проверено заново относительно новых значений nmi n и no p t . Если условие (4) по-прежнему выполняется, то за счет некоторого последовательного увеличения параметра n0 можно значительно сблизить с соблюдением условия (4) значения n и n . Необходимо отметить, что сте-m n        o p t пень такого сближения определяется возможностью разделения параметров nmi n и no p t при использовании критерия отбора оптимального решения [1]. Дело в том, что при их сближении возникают затруднения с определением точки оптимальных значений, однако на практике это не сказывается на точности метода. В то же время необходимость в максимальном сближении величин nmi n и no p t чаще всего не возникает, т. к. требуемая точность решения обратной задачи реализуется гораздо раньше.

В работе [4] изучается переход точки минимума ( d _min , n _min ) через точку оптимальных значений ( d_opt , n_opt ) , причем рассматривается не только сближение, но также и процесс расхождения этих точек. Мы не будем здесь затрагивать особенности такого перехода, для практических целей они не имеют существенного значения. В то же время в том же духе, как это сделано выше для процесса сближения точки минимума и точки оптимальных значений, целесообразно рассмотреть процесс расхождения этих точек. Данный процесс происходит при выполнении условия, противоположного условию (4)

n min >  n opt .                     ⁽¹⁷⁾

При задании параметров n ₀ и κ ₀ в двумерном пространстве ( d , n ) определяется траектория, ведущая к точке минимума ( d _min , n _min ) . На этой траектории устанавливается точка оптимальных значений ( d_opt , n_opt ). Параметры n _min и n_opt , удовлетворяющие условиям (17), соответствуют одной из таких траекторий.

Для удобства для некоторых параметров введем новые обозначения, позволяющие легко различать процессы схождения и расхождения точек. Для параметров, определяющих процесс схождения точек, включая начальное значение n ₀ ⁽⁰⁾ , оставим прежние обозначения. В то же время введем параметры, определяющие степень принятого максимального сближения точки минимума и точки оптимальных значений:

n 0-),     nm-in,     nop.

Величины (18), очевидно, удовлетворяют условиям n 0-) ^ n 00),    nmin < nop.

Для описания процесса расхождения точек введем параметры n0+),    nmL    n^t.(20)

Для них имеют место соотношения, аналогичные условиям (19):

nо+) > nо-),    nmin > nop.(

Определим величины (20), исходя из соображений симметрии по параметру nmi n относительно точки перехода. При этом будем иметь в виду, что величина n(-). и величина n(0)., отвечающая точке пе-o pt                        o pt рехода, различаются слабо. Их разность сущест- венно меньше разности nm^n - nOpt|. Поэтому величину nm+i)n можно определить соотношением

^{( + )        ( - )} Ги^{( - )       ( - )             (} )        ^{( - )}

ⁿ min n opt ' ⁽ n opt n min) n Opop t ⁿ min, v^-^v практически не нарушающим указанной симметрии.

Затем, аналогично тому как это сделано для процесса схождения точек (см. (13)–(16)), находим величину n 0 ^{+ )} , обеспечивающую значение n m ⁺ i) _n для параметра n в точке минимума. При этом на соответствующей траектории устанавливается точка оптимальных значений

( d o + 1 , n opt ),                          (23)

где величина n(+), относительно слабо отличается o pt от аналогичной величины no-p)t. Однако такой прием имеет в основном ориентировочное значение. На практике важно только, чтобы величина n0+), с которой связан скачок через точку перехода, незначительно отличалась от величины n0-). А в этом случае соотношение (22), определяющее параметр nm+i)n, может заметно нарушиться, что практически не скажется на положении точки (23).

В качестве примера рассмотрим второй вариант (см. (11)) экспериментальных ошибок. Как следует из работы [1], в идеальном случае, когда известны точные значения оптических параметров подложки, данный вариант приводит к следующим значениям параметров пленки в точке минимума:

d min = 2.825 нм; n min = 1.3877.       (24)

В рассматриваемом в настоящем разделе случае показатель преломления n0 подложки в отличие от коэффициента поглощения κ0 неизвестен. Определяя его выражением (12), т. е. принимая для него значение, меньшее точного, мы еще в большей мере снижаем величину nmi n , приближая ее к единице. Как выше отмечалось, значение (12) для параметра n0 нельзя использовать в качестве начального значения n0(0) . Но здесь нас интересует другое. Увеличивая параметр n0 до его точного значения, мы всего лишь повышаем величину nmi n до ее значения (24). Поэтому начальное значение n0(0) , подводящее величину nmi n к точке перехода, должно удовлетворять условию n0о) > (nо)tru.                   (25)

Для второго варианта экспериментальных ошибок можно остановиться на следующем начальном значении n0(0) :

n 00) = 3.86544.                (26)

Начальное значение (26) обеспечивает такое сближение точки минимума и точки оптимальных значений, которое целесообразно принять за максимальное сближение. Ему соответствуют сле- дующие величины:

n 0-) = n00) = 3.86544,(27)

dm-n = 2.5246, n» = 1.4914,(28)

dO-t = 2.5150, nop = 1.4957.(29)

Величину n0+) определим значением n0+) = 3.86550.(30)

Данной величине соответствуют параметры d■ = 2.493 8, n» = 1.5060,(31)

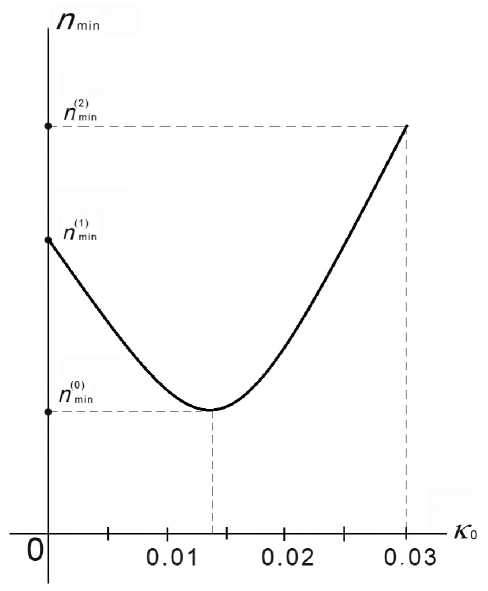
d

Как следует из выражений (27)–(29) и (30)–(32), ввиду близости величин n0^-)и n0⁺⁾отвечающие им оптимальные значения параметров сверхтонкой пленки различаются слабо. Сблизить их еще больше, сближая очень близкие величины n0^-)и n0⁺⁾, практически невозможно. Поэтому можем сразу, усредняя соответствующие величины, записать окончательные выражения для оптимальных значений показателя преломления подложки и параметров пленки

(n0)opt = 3.86547, dopt = 2.5149, nopt = 1.4959. (33)

Таким образом, показатель преломления подложки определяется с очень хорошей точностью. В то же время результаты (33) для параметров пленки несколько хуже тех, которые определены в работе [1] для случая подложки с известными оптическими константами. Это объясняется естественным понижением точности с увеличением числа неизвестных параметров.

Рассмотрим теперь общий случай, когда неизвестны все четыре параметра однослойной системы.

РЕШЕНИЕ ОБРАТНОЙ ЗАДАЧИ ОТНОСИТЕЛЬНО ВСЕХ ПАРАМЕТРОВ ОДНОСЛОЙНОЙ ОТРАЖАЮЩЕЙ СИСТЕМЫ

Основой для решения этой задачи являются результаты предыдущего раздела. Поскольку коэф- фициент поглощения подложки также подлежит определению, необходимо рассмотреть набор значений коэффициента κ0 , образующих некоторую последовательность (7). Имея в виду модель (10) отражающей системы, рассмотрим последовательность значений данного коэффициента, начиная от нуля и кончая значением 0.030. При этом от 0.00 до 0.020 коэффициент κ0 меняется с шагом 0.005, от 0.020 до 0.025 — с шагом 0.001, а после 0.025 сразу идет значение 0.030, — всего 11 значений. Для определенности по-прежнему будем рассматривать второй вариант из (11) экспериментальных ошибок. Как и в предыдущем разделе, необходимо определить параметры n00) и n0 1, n0+), а также nm-,),, no-pt и nm^, n,( p), имеющие тот же смысл. Это означает, что для этих параметров должны выполняться условия (19) и (21). Но при этом возникает очевидный вопрос, для каких значений κ0 должны определяться указанные параметры. Чтобы сравнить влияние различных значений к на величины nт-,)п, nopt и n», n' p), параметры n00) и n0-), n0+) должны быть определены для какого-то одного значения κ0 . В предыдущем разделе они определены для значения к0 = 0.023, и, поскольку здесь мы также рассматриваем второй вариант экспериментальных ошибок, целесообразно определить данные параметры для того же значения коэффициента κ0 . В соответствии с этим для параметров n00) и n0 1, n0+) примем значения (27) и (30). Что касается величин nm-^n, n^t и nт+,)п, np, то их необходимо определять для всех принятых значений κ0 . Однако очень важно, чтобы при любом значении к0 величины nm-,),, nO-,)t и nт+,)п, nO+>)t удовлетворяли условиям (19) и (21). Задав параметры n00) и n0-), n0+) выражениями (27) и (30), мы сохраним условия (19) и (21) для любого значения κ0 .

Определенный интерес представляет поведение величин nm-i), и nm+^n как функций параметра к₀

nm-.^Ki) и nткк,).            ⁽³⁴⁾

Поведение функций (34) изображено на рисунке. При переходе от одной функции к другой общий вид кривой не меняется, несколько изменяются только значения величин nm(0i)n , nm(1)in и nm(2i)n , а вот положение точки минимума на оси κ0 практически не сдвигается. Такой же вид имеет кривая nmin (κ0) для идеального случая, когда

Схематическое изображение зависимости nmin (κ0) показателя преломления n пленки в поляризационные углы V и А, определенные по параметрам (10), заданы без ошибок, параметры d , n и n0 также заданы их точными значениями, а неизвестным считается только коэффициент поглощения κ0 . И в этом случае положение точки минимума на оси κ0 остается практически тем же.

Необходимо установить признак, по которому может быть найдено оптимальное значение коэффициента κ0 . Исходя из общих соображений, предположим, что оптимальный коэффициент κ0 определяется тем значением, при котором наблюдается максимальное сближение соответствующих величин п^, и п^. Это предположение подтверждается поведением функций n^pt (ко) и n^pt (ко). (35)

Кривые, соответствующие этим функциям, пересекаются в одной точке, которой соответствует какое-то значение κ0 . При остальных значениях κ0 данные кривые заметно расходятся. По сделанному предположению точка пересечения кривых (35) и определяет оптимальное значение коэффициента κ0 . Если рассмотреть идеальный вариант, когда экспериментальных ошибок нет, а параметры, определяемые все теми же соотношениями (10), считаются неизвестными, то использование описанного признака позволяет определить параметры однослойной системы (10) с огромной точностью. Это подтверждает справедливость сделанного предположения.

Наравне с функциями (35) можно рассматривать также и функции do-t (kJ и do +t (ko).                 (36)

Кривые, соответствующие функциям (36), пересекаются в точке, которая также определяет оптимальное значение коэффициента κ₀. Кривые (36) в их относительном расположении могут быть даже более выразительными, нежели кривые (35).

Используя описанный признак, определим оптимальное значение коэффициента поглощения κ₀ подложки для второго варианта экспериментальных ошибок. Точка пересечения кривых (35), как и точка пересечения кривых (36), дает следующее значение

(Ko)opt « 0.0232.                (37)

Те же точки пересечения кривых дают окончательные выражения и для оптимальных значений d_{o pt} и n_{o pt} пленки. Показатель преломления n₀ подложки определяется так же, как и в предыдущем разделе. Окончательные выражения для параметров системы следующие:

(no)opt = 3.86547, (Ko)opt « 0.0232,      (38)

dopt = 2.5180, nopt = 1.4950.             (39)

Таким образом, метод последовательных приближений, разработанный ранее, не только упрощен, но и значительно усовершенствован. Это касается прежде всего признака, по которому устанавливается оптимальное значение коэффициента поглощения подложки. Новый вариант метода может быть успешно применен для исследования поверхностной структуры различных объектов. Следующая работа будет посвящена исследованию, причем на основе реального эксперимента, поверхностной структуры жидкостей.