Исследование процесса контактной приспособляемости при кулоновском трении упругих тел

следней необходимо принимать во внимание максимальное значение f. Для изучения условий возникновения приспособляемости многие авторы использовали численные методы и прежде всего МКЭ [3, 5, 6]. Однако, до сих пор не был решен вопрос обоснованности выбора размера конечно-элементной сетки. В качестве минимального значения рекомендуется принимать 6÷6.5 мкм [5, 6], но какие-либо физические аргументы или вычислительные аспекты этого выбора отсутствуют.

В данной статье методом конечных элементов моделируется взаимодействие двух упругих тел с различной геометрией краев и при различных сочетаниях свойств материалов. На основе этих результатов обосновывается целесообразность и выполняется обобщение теоремы контактной приспособляемости на случай взаимодействия многих тел.Для решения задачи определения условий, при которых система приводится в состояние контактной приспособляемости, методом конечных элементов в программном комплекс ANSYS анализировалась контактная задача взаимодействия двух тел (рис.1). Нижнее тело закреплено по боковым линиям и снизу. Производится нагружение верхнего тела. На первом шаге нагружения к верхней поверхности этого тела прикладывается вертикальная равномерно распределенная нагрузка P . На последующих шагах эта нагрузка остаётся постоянной, а знакопеременная горизонтальная нагрузка Q прикладывается к верхней или боковой поверхностям (рис. 1).

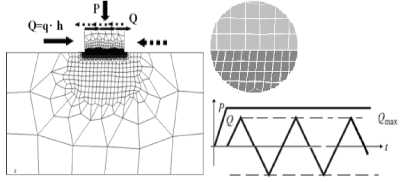
Рис. 1 . Конечно-элементная модель взаимодействия двух тел.

Нижнее тело закреплено по боковым линиям и снизу, а нагружение верхнего тела соответствует графику: нормальная сила Р постоянна, касательная сила изменяется линейно в диапазоне ±Q max . Касательная нагрузка прикладывается к верхней поверхности или к вертикальным граням верхнего тела. Отдельно показана сетка конечных элементов в зоне контакта.

Из результатов расчетов, показанных на рис. 2, следует, что в координатах (Q/P) max – f можно выделить области с различным характером контактного взаимодействия. При относительно больших значениях коэффициента трения первоначальное нагружение не приводит к возникновению на контактной поверхности зон частичного скольжения – имеет место сцепление по всей поверхности. Эта область на диаграммах (Q/P) max – f ограничена сверху линией 1. При малых значениях коэффициента трения полного сцепления при первоначальном нагружении не наблюдается – сразу возникает частичное скольжение. Выше линии 1 находится область частичного скольжения, в которой имеет место частичная или полная контактная приспособляемость при циклическом нагружении силой Q . Частичная приспособляемость состоит в уменьшении зоны проскальзывания и его величины с ростом числа циклов. Эта область сверху ограничена линией 2 (рис.2). Выше линии 2 располагается область, где при циклическом нагружении имеет место проскальзывание, не уменьшающееся с числом циклов. Область полного скольжения находится выше прямой 3, для которой выполняется равенство (Q/P) max =f .

Кроме того, на рис. 2 проведена линия 4, разделяющая области с разным характером скольжения. Выше неё находится область, для которой скольжение в любой момент времени наблюдается вблизи обоих краёв контактной поверхности. Ниже линии 4 проскальзывание отмечается только с одной стороны: при малых коэффициентах трения проскальзывание только с передней по направлению силы Q стороны, при больших – только с задней стороны.

Сравнение графиков показывает, что характер контактного взаимодействия зависит не только от отношения внешних сил, но и от места приложения силы Q . При реверсном нагружении горизонтальной внешней силой, приложенной к верхней плоскости, система воспринимает без частичного скольжения более высокие значения соотношения (Q/P) mах (рис. 2а, б). Это объясняется разным характером распределения контактных усилий при нагружении по этим двум схемам.

Рассмотрим влияние размера сетки конечных элементов. На рис. 2в показаны результаты расчета для случая задания на контактной линии 1000 элементов; 2г – 50 элементов. Для модели, расчеты которой представлены рисунком 2г, в области между линиями 1 и 2 наблюдается наступление сцепления по всей контактной поверхности, что соответствует полной контактной приспособляемости.

При увеличении числа конечных элементов в зоне контакта (рис. 2в) приспособляемость – исчезновение зоны скольжения – не достигается, хотя и происходит уменьшение этой зоны. Частичное проскальзывание возникает при значениях касательных сил близких к Q max .

Заметим, что избежать это проскальзывание можно, если максимальная нагрузка первого цикла будет превышать её значение на последующих циклах. Таким образом, наступление полной контактной приспособляемости в рассмотренных случаях происходит только тогда, когда поверхность контакта имеет соответствующий относительно небольшой линейный размер.

Из графиков видно также, что приспособляемость наблюдается при относительно больших значениях коэффициента трения.

Как уже указывалось, f значительно возрастает в процессе циклического проскальзывания. Например, для сплава Al/4%Cu коэффициент трения увеличивается от 0,2 до 0,6 ÷ 0,75, а для сплава Ti-6Al-4V – от 0,45 до 0,55 за 5000 циклов [2, 4]. Поэтому при оценке возможности контактной приспособляемости следует учитывать возросшее значение коэффициента трения.

Взаимодействие упругих тел идеальной прямоугольной формы не позволяет оценить возможность приспособляемости на крае контактной поверхности из-за возникающей здесь сингулярности. При аппроксимации прямоугольного края мелкими КЭ наблюдается резкое возрастание касательных напряжений и край скользит. Моделью реального контактного взаимодействия может послужить тело, край которого скруглён. Результаты расчетов представлены в координатах (Q/P)_max – f на рис. 2д.

Сопоставление результатов моделирования трения тел с одинаковыми и различающимися упругими свойствами (рис. 2б, е) показывает важность учёта этого фактора. Из рисунка видно, что для тел, обладающих разными упругими свойствами, область контактной приспособляемости сдвинута в сторону больших значений f и соответствует большим значениям отношения (Q/P) max . Результаты моделирования подтверждают возможность наступления контактной приспособляемости, как на это указывают теоретические результаты [2, 3]. При этом оказывается, что полное прекращение частичного проскальзывания при циклическом нагружении зависит от размера контактной поверхности: полная приспособляемость наступает при малых размерах.

Когда поверхность контакта имеет большие размеры, то вместо полной приспособляемости при циклическом нагружении наблюдается существенное уменьшение зоны и величины частичного проскальзывания, то есть наступает частичная приспособляемость. Однако, даже частичное уменьшение размера зоны и величины контактного проскальзывания представляется важным для обеспечения долговечности деталей при фреттинге.

Теоремы приспособляемости, сформулирован- ные в работах [1, 7], записаны для случая контакта двух тел. Ниже приводится обобщение этих теорем на случай системы, состоящей из произвольного числа контактирующих между собой упругих тел.

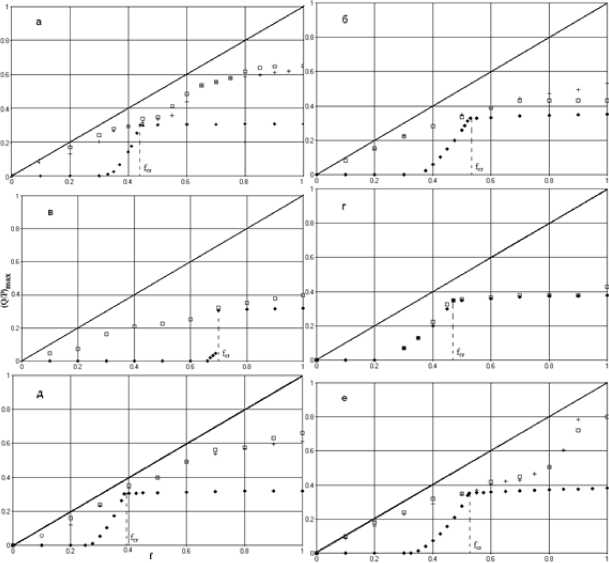
Рис. 2. Области с различным характером контактного взаимодействия двух телв координатах (Q/P) max – f : * * * * – линия 1 – верхняя граница зоны полного сцепления при первоначальном приложении силы Q;

□ □ □ D – линия 2 – граница зон полного сцепления и частичного проскальзывания при циклическом нагружении;         – линия 3 – граница между зонами частичного и полного скольжения;

+ + + + – линия 4 – граница между зонами одностороннего и многостороннего проскальзывания;

а - к верхней поверхности прикладываются распределенные силы P и Q. Тела прямоугольной формы, упругие свойства тел одинаковы ( E =2.1^.10¹¹H/м², μ =0.3). На контактной линии 100 элементов; б - сила Q распределена по вертикальной грани. Тела прямоугольной формы, упругие свойства тел одинаковы ( E =2.1^.10¹¹H/м², μ =0.3).

На контактной линии 100 элементов. в - сила Q распределена по вертикальной грани. Тела прямоугольной формы, упругие свойства тел одинаковы ( E =2.1^.10¹¹ H/м², μ =0.3). На контактной линии 1000 элементов;

г - сила Q распределена по вертикальной грани. Тела прямоугольной формы, упругие свойства тел одинаковы( E =2.1^.10¹¹H/м², μ =0.3). На контактной линии 50 элементов. д - сила Q распределена по вертикальной грани. Край контактной линии имеет скругление, упругие свойства тел одинаковы ( E =2.1^.10¹¹H/м², μ =0.3). На контактной линии 100 элементов.е - сила Q распределена по вертикальной грани. Тела прямоугольной формы, упругие свойства различны (верхнее тело – E =2.1^.10¹¹H/м², μ =0.3; нижнее тело – E =3.5^.10¹⁰H/м², μ =0.15). На контактной линии 100 элементов.

Рассмотрим конструкцию, состоящую из N упругих элементов, между которыми реализуются контактные условия сухого трения. В предположении линейной упругости для элемента α, где α =1,2,.., N ,

α

можно записать связь тензоров деформаций ε

и

α

напряжений σ в виде закона Гука:

α  αα

8α Aα a ,      i, j, k, l = 1,2,3, ij        ijkl kl где A α – компоненты обратного тензора Гука.

На конструкцию действуют некоторые постоянные или циклически изменяющиеся внешние силы.

Пусть r – распределенные по контактной поверхно-

α*

сти силы, а s – перемещения. Напряжения a со ответствуют состоянию конструкции, при котором проскальзывание всех элементов по контактным поверхностям отсутствует – они «сварены» друг с ~α другом, a –дополнительное самоуравновешенное поле напряжений, соответствующее случаю отсут-α ствия проскальзывания, a – самоуравновешенное поле напряжений без этого условия. Тогда для безопасное поле напряжений в конструкции, отвечающее условию отсутствия скольжения по контактным

Л     Л Ct _ гх        _ поверхностям: S = 0, 8- — 0 всех а записывается

α α* α в виде e σ     σ ; а поле напряжений при на личии скольжения: S ^ 0, 8a Ф 0 в виде

ij

α   α*α

σ σ ij       klkl

Определим меру разности смещений, вызванных скольжением по отношению к «сваренному» состоянию, и смещений, соответствующих безопас- ным силам, в функционала N Π

α 1Ωα виде положительно определённого

α ααα α

^A ijkl ^{( σ} ij   ^eij^{)( σ} kl   ^ekl^{)dΩ 0}

Дифференцируя по времени и учитывая теорему о взаимности работ, получаем

N

11 = 2 X f ( ° j-ej)8“dQ .

α 1Ω _α

Введем следующие обозначения: p , τ – нормальное и касательное составляющие контактных усилий, υ , ω – нормальное и касательное составляющие перемещения s . Вектора безопасных сил – когда скольжение отсутствует – лежат внутри конуса трения Кулона τ f p .

Как уже указывалось, в работах [1, 7] доказательство теоремы о контактной приспособляемости получено в предположении, что нормальная составляющая поверхностных сил не зависит от касательных смещений и, следовательно ~p   p .Очевидно, что данное условие можно заменить более слабым требованием, состоящим в том, что вектор сил взаимодействия в каждой точке контактной поверхности не выходит за пределы такие, что (г - ~) • s < 0 (рис. 3).

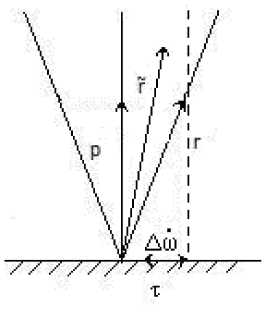
Рис. 3. Безопасные силы r~ принадлежат области конуса трения Кулона: проекция вектора r  r~направлена внутрь круга радиуса f p для ~p  p , причем ~p  p .

Для каждого элемента справедливо равенство α αα

( ° kl  ekl^{) e} kld^ ^и

Ωα

J(,P   ~)U)dS + j( т -~)cbdS , a = 1 ,2,..., N , где Q_a

S

S

– область, занимаемая элементом,

S_a - его поверхность, тильдой отмечены значения, соответствующие случаю отсутствия проскальзывания.

Поскольку на границах двух элементов усилия взаимно уравновешены, зависимость (2) с учётом (3) можно переписать в виде

П = 25 J (т в -~в )АсЬв dS, β Sβ где - номер контактной поверхности между эле ментами, Р = 1,., АсЬ^ - скорость скольжения.

Таким образом, для упругих систем с кулонов- ским ния,

трением в условиях цикли-ческого нагруже- если

скалярное

произведение

(( т р “ ~в ), АЬв^ отрицательно, что равнозначно условию (г - 7) • s < 0, то скорость П < 0 . Поскольку функционал П >  0, то условие отрицательности его скорости в данном случае является необходимым и достаточным условием контактной приспособляемости.

Численный расчет с использованием МКЭ для системы из большего двух числа упругих тел подтверждает возможность наступления в этом случае контактной приспособляемости. В качестве модели использовалась конструкция из тел прямоугольной формы, имеющих как горизонтальные, так и вертикальные контактные поверхности (рис._4).

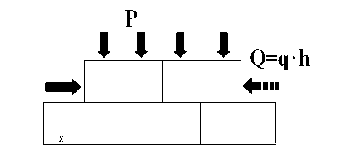
Рис. 4. КЭ модель контактного взаимодействия нескольких элементов прямоугольной формы, имеющих как горизонтальные, так и вертикальные контактные поверхности.

При количестве КЭ менее 50 на каждой поверхности наблюдается наступление полной приспособляемости в случае, когда, например, изменение нормальных и ка-сательных сил при f=0.75 находится в диапазоне значений, ограниченном сверху (Q/P)_max = 0.43.

Полученные результаты используются при моделировании поведения элементов шарошечной сборки. Характерными видами износа шарошечных долот является выпадение зубков и образование трещин в шарошке. Под действием длительного циклического нагружения между элементами сборки в области контакта возникают зоны сцепления и скольжения. Наличие скольжения в контакте – одна из причин указанных разрушений. Следуя теории фрикционного взаимодействия в данном случае можно значительно уменьшить зону скольжения в контакте, тем самым увеличить срок эксплуатации шарошки. В целях изучения полей трения между элементами шарошечной сборки в программном комплексе ANSYS построена конечно-элементная модель. На поверхностях взаимодействия генерировались контактные элементы. Твердосплавные зубцы в венцах шарошки имеют предварительный натяг. В расчете скольжения зубца относительно отверстия конуса прикладывалась реверсная нагрузка к его вершине. На контактной поверхности (рис.5) отмечены поля скольжения и сцепления.

Рис. 5 . Контактная поверхность отверстия шарошки долота под зубком.

Уменьшение одних и увеличение других соответственно, от цикла к циклу является предпосылкой для повышения износостойкости шарошек бурового долота.