Исследование процесса кристаллизации влаги в кирпиче
Автор: Желдаков Дмитрий Юрьевич, Козлов Владимир Владимирович, Кузнецов Дмитрий Валерьевич, Синицин Дмитрий Александрович
Журнал: Нанотехнологии в строительстве: научный интернет-журнал @nanobuild
Рубрика: Строительное материаловедение
Статья в выпуске: 6 т.12, 2020 года.
Бесплатный доступ
Решение вопросов поведения влаги в материале ограждающих конструкций особенно при знакопеременных температурах очень важно для обеспечения правильного расчета сопротивления теплопередаче ограждающей конструкции и в конечном счете создания комфортных условий проживания. Однако до настоящего времени в практике исследований характеристик материалов, применяемых в ограждающих конструкциях зданий, нет методики определения температуры кристаллизации влаги в материале, находящемся в твердой фазе. В основу исследований положен тезис, что вода, поступающая в материал ограждающей конструкции, в результате процесса гидролиза некоторых элементов, находящаяся в материале конструкции в виде оксидов и солей, представляет собой эвтектический раствор с непостоянным составом и концентрацией. Таким образом исследование процесса кристаллизации влаги переходит из области микро (при рассмотрении вопроса определения температуры кристаллизации по размерам пор материала) в область нано при исследовании эвтектического раствора при условии возможного образования гидратов. Для лабораторного исследования процесса замерзания влаги, с учетом того, что процесс замерзания и оттаивания влаги в твердом теле изучается при значительной разнице в массе жидкой и твердой фаз, разработана методика эксперимента. Методика максимально упрощена с учетом широкого применения в производственных условиях. Простота методики получения экспериментальных результатов компенсируется разработанным математическим аппаратом обработки результатов исследований. Математическое решение задачи основано на сравнении поведения кривых замерзания образца в сухом и насыщенном влагой образцах. Разработанный метод позволил кроме температуры замерзания влаги получить дополнительные характеристики состояния влаги, такие как количество незамерзшей влаги в материале конструкции, температура переохлаждения, теплоемкость влаги в жидком и твердом состояниях,концентрация растворенных веществ. Знание концентрации растворенных веществ в материале, даже при условии отсутствия точного состава этих веществ, позволит управлять температурой замерзания влаги на уровне нанотехнологий.
Поровая структура материала, кристаллизация влаги, температура переохлаждения, математическое моделирование процесса теплообмена
Короткий адрес: https://sciup.org/142225545
IDR: 142225545 | УДК: 666.972.16 | DOI: 10.15828/2075-8545-2020-12-6-305-312
Текст научной статьи Исследование процесса кристаллизации влаги в кирпиче
Предметом исследования является изучение поведения влаги в ограждающих конструкций при знакопеременных нагрузках. Объектом исследования – материал строительной керамики. Вопрос увлажнения материала ограждающей конструкции – один из основных вопросов, решаемых в области строительной физики. От его решения во многом зависят долговечность, гигиеничность и энергоэффективность ограждающих конструкций [1, 2, 3]. Наличие влаги в материале кирпичной кладки значительно влияет на ее прочность [11, 12, 13]. Среди прочего при расчете влажностного режима ограждающей конструкции необходимо знать количество незамерзшей влаги в конструкции при любой температуре.
СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ
Задачей данной работы является создание методики математической обработки результатов лабораторных исследований процесса замерзания влаги в материале кирпича.
До настоящего времени в практике исследований характеристик материалов, применяемых в ограждающих конструкциях зданий, нет методики определения температуры кристаллизации влаги [4, 5]. Уникальность поставленной задачи исследований состоит в следующем:
-
• во-первых, изучается процесс замерзания и оттаивания влаги в твердом теле при значительной разнице в массе жидкой и твердой фаз;
-
• во-вторых, влага рассматривается как раствор сильных электролитов с очень низкой концентрацией [6,7,8];
-
• в-третьих, учитывается, что состав растворенных в воде элементов постоянно меняется в зависимости от наружных условий и исходного элементного состава твердого материала [9, 10, 14, 15, 16].
До настоящего времени при переходе температуры ограждающей конструкции через ноль процесс кристаллизации рассматривался как процесс замерзания воды в порах материала. Изменение количества незамерзшей воды в материале при разных отрицательных температурах объяснялось размерами пор материала. В данной работе влага в материале рассматривается как эвтектический раствор, полученный в процессе гидратации некоторых оксидов и солей, входящий в состав материала. Такой подход определяет изучение процесса кристаллизации воды из раствора при условии образования нановеществ в виде гидратов солей. При условии возможности определения концентрации солей в растворе возникает возможность управления процессом замерзания влаги в ограждающих конструкциях на основе нанотехнологий изменения исходного состава материала.
Целью исследования является разработка методики лабораторного эксперимента и методики математической обработки полученных в эксперименте данных для определения температуры кристаллизации влаги, количества незамерзшей влаги в материале, температуры переохлаждения, концентрации растворенных веществ, теплоемкости влаги в жидком и твердом состояниях.
В данной статье описывается только методика математической обработки результатов эксперимента. Описание методики и результатов самого эксперимента, а также результаты, полученные с применением описываемой методики математической обработки, будут опубликованы авторами позже.
Математическое описание эксперимента
В общем случае процесс теплопереноса в исследуемом образце описывается трехмерным уравнением теплопроводности с граничными условиями третьего рода:
dt d dt \ d dt \ d dt \
CY~ = ~ T~ Ц1T" “7“ ^2 7— “ — Цз ' dz дхг к 1 дхх) Эх2 к z дх2) дх3 к 5 дх3)
где x 1, x 2, x 3 – координаты, м;
-
λ1, λ2, λ3 – расчетные теплопроводности по соответствующим направлениям, Вт/(м•oC);
с – удельная теплоемкость материала, Дж/ (кг•oC);
γ – плотность материала, кг/м3;
z – время, с.
На границе образца происходит теплообмен с воздухом в морозильной камере. Предполагается, что образец имеет форму параллелепипеда и на всех гранях образца теплообмен протекает одинаково (поскольку более детальной информации об этом процессе нет). Поэтому ниже приведено граничное условие только для одной из граней.
При расположении осей системы координат вдоль ребер образца граничное условие принимает вид:
λ (∂ t /∂ x ) = αн ( t н– t ), (2)
где t н – температура в морозильной камере, оС;
αн – коэффициент теплообмена в морозильной камере, Вт/(м2•оС).
По сути формулы (1), (2) описывают перераспределение теплоты по образцу вследствие теплообмена с окружающей средой. В качестве начальных условий принимается равномерное распределение по образцу температуры t0, измеренной в эксперименте.
На гранях расчетного участка, контактирующих с воздухом морозильной камеры, будут выполняться граничные условия (2). На гранях расчетного участка, разрезающих образец, вследствие симметрии задачи записываются граничные условия второго рода, поток теплоты равен нулю, т.е. в условиях исследуемой задачи производная температуры по координате равна нулю:
Аналогично записываются условия по остальным координатам.
Вследствие симметрии системы решение уравнения и граничных условий ищутся с помощью разделения переменных. Для краткости опустим ход решения и запишем сразу конечную формулу:
СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ
, (4)
где коэффициенты η1, η2, η3 находятся из граничных условий, а коэффициент B – из начальных.
Для практического использования достаточно только первого члена ряда, т.е. формулы (4), в которой коэффициенты η1, η2, η3 были определены из уравнения (5) на первом периоде тангенса в положительной полуплоскости:
V^h^ta^V^h^) = ^. (5)
Доказано, что разброс температуры по образцу не оказывает существенного влияния на исследуемые закономерности вне участка фазовых переходов. Единственный процесс, при котором разброс температур может оказать искажающее воздействие – фазовый переход. Но фазовые переходы характерны только для увлажненных образцов, теплопроводность которых значительно больше, чем у сухого образца. Теплопроводность существенно влияет на разброс температур по образцу, сглаживает его. Не приводя всех выкладок вновь, укажем только, что для исследованного увлажненного образца разброс температур между самой теплой и самой холодной точками составил всего 14% от общего температурного перепада. Средняя температура и температура в месте расположения датчика в точности совпали.
Влияние разброса температур на точность измерения фазового перехода требует дополнительного изучения. Но благодаря полученным решениям уже сейчас можно указать организационные мероприятия, способствующие повышению точности измерений.
Используя испытуемые образцы достаточно малых размеров и с высокой теплопроводностью, можно пренебречь отклонением температуры в разных точках образца от среднего значения.
Это позволяет упростить математическое описание задачи, сведя его к теплообмену материальной точки с заданными свойствами теплообмена и теплоемкости.
Математическая модель для теплообмена материальной точки сводится к линейному дифференциальному уравнению первой степени:
cm •(∂ t /∂ z ) = S αн ( t н– t ), (6)
где m – масса образца, кг;
S – общая площадь поверхности образца, участвующей в теплообмене, м2.
Нужно дополнительно заметить, что под cm в уравнении (6) понимается обобщенная теплоемкость образца, которая из-за фазовых переходов в процессе эксперимента меняется. Аналогично Sαн – это обобщенный коэффициент теплообмена образца, который может меняться в процессе эксперимента из-за особенностей работы морозильной камеры.
Из соображений удобства далее часто будет использоваться сдвинутая температура
τ = tн+t.(7)
Для решения уравнения (6) требуется только одно граничное условие. Это начальное условие
t(0) = t0.(8)
Общий вид решения:
t(z) = tн+(t0–tн) e–kz,(9)
где k – показатель экспоненты, определяемый по формуле k = Sαн/cm.(10)
Зависимость температуры от времени (9) должна получаться при проведении измерений на сухих образцах, для которых изменения характеристик образца и морозильной камеры за время проведения испытаний малы.
Постановка и результаты лабораторного эксперимента
Для проведения исследований был отобран кирпич марки М 100 с известным элементарным химическим и кристаллическим составом.В соответствии с условиями разработанной программы исследований испытания проводились на сухих образцах и образцах со 100% водонасыщением. Результаты эксперимента для сухих образцов представлены на рис. 1, для водонасыщенных образцов – на рис. 2.
На рис. 1 показано распределение температуры, полученное в эксперименте для сухого образца. На рис. приведен график сдвинутой температуры и аппроксимация зависимости экспонентой. Видно, что экспериментальные точки практически идеально ложатся на экспоненту. На графике опущены начальные и конечные точки, так как процесс в эти моменты времени сильно искажен. В начальный момент возмущение, связанное с установкой в камере теплого образца, приводит к значительному изменению температуры в камере. Пока эта температура восстанавливается, t н быстро изменяется, а значит на этом участке формула (9) не является решением уравнения (6). На конечном участке нарастает
СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ
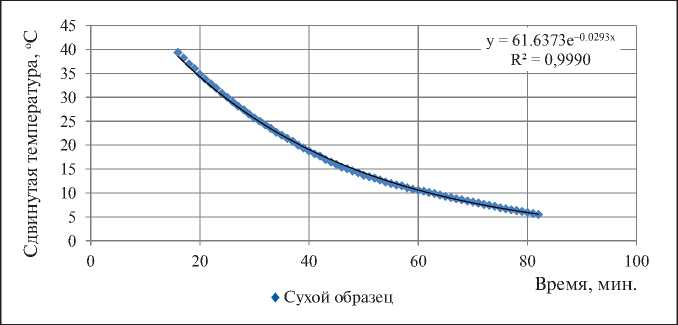
Рис. 1. Зависимость сдвинутой температуры от времени для сухого образца
погрешность, связанная с двумя факторами. Первый – температура в камере не постоянна, а переменная с периодическим изменением на ±1,5оС (период изменений 44 минуты). Второй – погрешность округления. Температура фиксируется датчиками с точностью до одной десятой градуса. Это не имеет значения, когда общий перепад температуры между образцом и камерой составляет десятки градусов, но со сближением этих температур погрешность округления начинает составлять все большую часть от общего перепада и на последнем участке приводит к погрешностям в десятки процентов.
Для влажного образца должно происходить сразу несколько изменений в графике. Сплошной экспоненциальный график должен разделиться на три участка. Два участка также экспоненциальные более пологие, чем для сухого образца, так как показатель экспоненты уменьшится за счет добавочной тепло- емкости воды (на участке отрицательных температур льда), и один участок горизонтальный во время замерзания воды в порах материала около 0оС. Так график должен был бы выглядеть для дистиллированной воды в достаточно крупных порах. Но на практике в большинстве строительных материалов вода превращается в раствор, поры в том числе и мелких размеров, и возможен еще ряд факторов, влияющих на замерзание.
Оценим погрешность вычислений, возникающую при нахождении показателя экспоненты по формуле (10). При этом принимаются следующие значения первичных погрешностей. Температуры измеряются с погрешностью 0,05оС, время – с погрешностью 0,5 с. При вычислениях все погрешности величин обозначены добавлением символа δ.
Проведенная обработка позволяет найти местные значения с намного большей определенностью. Отклонение от среднего значения меньше 2,5%
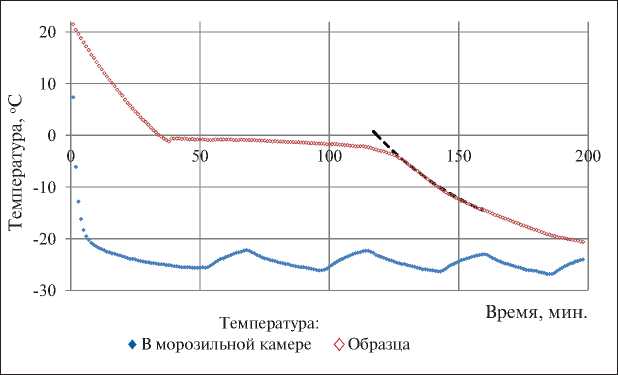
Рис. 2. Изменение температуры в камере (синие маркеры) и температуры образца (красные полые маркеры) в ходе испытаний полностью увлажненного образца
при температуре образца выше 5оС, и меньше 4% при температуре образца от –5оС до 5оС, что значительно лучше неопределенности в нахождении k по рис. 2.
Масса образца и его размеры известны с высокой точностью. Поэтому, зная удельную теплоемкость материала образца, по формуле (11) можно определить коэффициент теплообмена в морозильной камере. И наоборот, зная коэффициент теплообмена в морозильной камере, можно определить удельную теплоемкость материала образца.
Исследование влажного образца
Протекание процесса замораживания совместно со значениями температуры в морозильной каме-
СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ ре показано на рис. 3. Температура в морозильной камере, за несколько минут скомпенсировав возмущение от установки теплого образца, далее изменяется пилообразно с амплитудой в 1,5оС и периодом примерно 45 минут. Колебания температуры в морозильной камере снижают точность измерений, особенно при температуре образца, приближающейся к температуре камеры. В связи с этим результаты, при которых температура образца отличалась от температуры в морозильной камере, менее чем на 5оС не использовались.
На рис. 2 показано изменение температуры в камере (синие маркеры) и температуры образца (красные полые маркеры) в ходе испытаний полностью увлажненного образца.
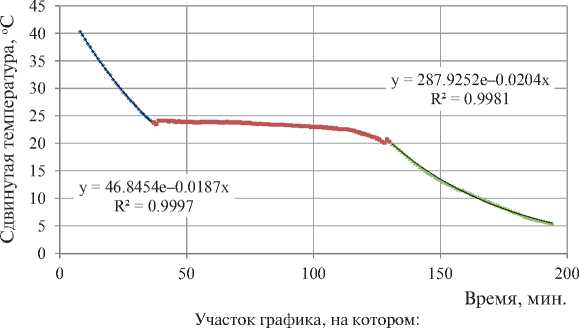
♦ Незамерзший раствор ■ Переходная фаза ▲ Замерзший раствор
Рис. 3. Зависимость сдвинутой температуры образца от времени в ходе испытаний полностью увлажненного образца
Видно, что замерзание раствора не начинается при 0оС. Образец сначала охлаждается до –1,3оС, а затем происходит почти мгновенный отскок до –0,6оС.
Первым шагом обработки результатов эксперимента необходимо убедиться, что на участках вне фазовых превращений температура образца изменяется по экспоненциальному закону. На рис. 3 показана зависимость сдвинутой температуры образца от времени в ходе испытаний. Ориентировочные участки экспоненциального развития и фазового перехода выделены цветами. Особенность графика в том, что для экспоненциальных участков с положительной и отрицательной температурами выбраны разные температуры морозильной камеры t н. Это сделано для повышения точности нахождения коэффициентов экспоненты, так как при проведении эксперимента температура в камере изменялась. Выбранные t н найдены осреднением соответствующих участков графика.
Визуально смена температуры в морозильной камере при обработке приводит к вертикальному сдвигу графика на 128 минуте. Этот сдвиг обусловлен не протеканием процесса, а особенностями обработки результатов.
Как видно из рис. 3 крайние участки с высокой точностью описываются экспонентой. Здесь в отличие от графика для сухого образца показатель экспоненты изменяется и равен 0,0187 мин–1 до фазового перехода и 0,0204 мин–1 после фазового перехода. Изменение показателя экспоненты, очевидно, связано с изменением теплоемкости образца за счет замерзания раствора (теплоемкость воды примерно в 2 раза выше теплоемкости льда).
Так как температура в морозильной камере в процессе измерений постоянно изменялась в сумме на несколько градусов, для повышения точности определения показателя экспоненты необходимо перейти к местным значениям, определяемым по формуле (10). Такая обработка проведена отдельно для участка с положительными температурами (незамерзшим раствором) и участка с отрицательными температурами (полностью замерзшим раствором). При обработке учитывался обнаруженный ранее эффект изменения теплообмена при работе и отключении холодильной машины.
На рис. 5 черная пунктирная линия показывает экспоненциальную аппроксимацию значений для температуры образца ниже –8оС. Место, где происходит расхождение экспоненциальной линии и результатов измерения (–4,5оС), укрупненно показано на рис. 4. Эта точка приблизительно указывает на момент полного замерзания раствора. На самом деле стопроцентное замерзание раствора происходит при эвтектической температуре и не зависит от начальной концентрации, поэтому скорее всего в этом месте точность исследований становится недостаточной для суждения об остаточных фазовых переходах в материале.
Более полно и точно изучить процесс замерзания раствора, в том числе место стопроцентного замерзания, можно прямым расчетом количества незамерзшей влаги из теплового баланса на участке фазового перехода. Все подготовительные работы для этого проведены, вспомогательные величины найдены по экспериментальным данным с максимальной достижимой точностью.
В общем случае за 1 минуту между измерением температуры образца замерзает масса раствора, которую можно найти по формуле
СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ
_ S aH(/H -r)Az-(cBmK +cBmB +с„(тв0 mj)A/ . an
, (11)
s где λр – удельная теплота плавления раствора, Дж/кг.
Формула (11) находится из предположения, что вся разница между энергией, отданной образцом в морозильную камеру, и энергией остывания образца получена от кристаллизации раствора. Если использовать эту формулу непосредственно, то погрешность нахождения коэффициента теплообмена и удельной теплоемкости будет суммироваться с погрешностью удельной теплоты плавления и прочими более мелкими погрешностями. Из-за этого погрешность результата будет очень велика.
Формулу (11) можно преобразовать так, чтобы исключить параметры с наибольшей погрешностью нахождения:
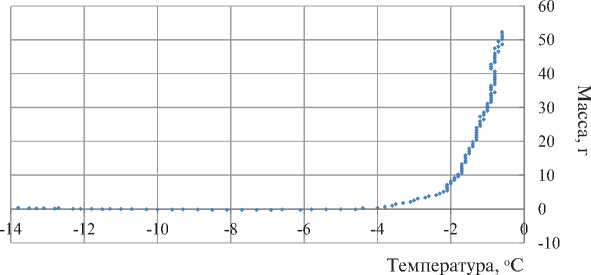
t _t_w±±w±±s^ _ ” 5aHAz AmB=---------------, (12) p 5ан Az 1 . tB-t--Af _ k(mB)kz AmB =--------. (13) p 5aH Az Показатель экспоненты изменяется в процессе замерзания раствора, так как удельная теплоемкость воды и льда отличается. Величина, обратная к показателю экспоненты, линейно зависит от массы незамерзшей воды. Таким образом, достаточно точно зная показатель экспоненты в двух точках, мы можем провести прямую линию и находить обратную величину без потери точности. Используя экспериментальные данные, можно определить показатель экспоненты при 0оС k1 = 0,00031 с–1 и показатель экспоненты при –6оС k2 = 0,00035 с–1. Тогда 1 I m - + B -2857 + 6827mE. (14) k(mB) кг kjm^ Формула (14) соответствует включенной холодильной машине. При выключенной холодильной машине значения, полученные по формуле (14), нужно умножать на 1,1. Формула (14) позволяет построить график зависимости незамерзшей воды от температуры. Во многом нам заранее известна форма этой кривой, поэтому ее построение помогает уточнить неопределенные параметры. Для построения кривой необходимо задаться значением λр/Sαн, детализировать изменения этого параметра изменением температуры слишком сложно, и возникающая при этом погрешность превысит выигрыш, в точности получаемый при детализации. Исходя из ранее проведенных исследований для сухого образца и табличного значения теплоты плавления чистого льда, равной 330 кДж/кг, λр/Sαн = 1997000оС•с/кг. Из-за невысокой точности определения коэффициента теплообмена предварительную погрешность нахождения параметра λр/Sαн можно оценить в 10%. График зависимости массы незамерзшей воды от температуры показан на рис. 5. Красная пунктирная линия показывает начальную массу раствора. Асимптота совпадает с нулем. Отклонение Рис. 4. Точка полного замерзания раствора в порах материала СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ ♦ Незамерзший раствор Рис. 5. График зависимости массы незамерзшего раствора от температуры точек на горизонтальном участке графика от нуля показывают реальную погрешность расчетов. Они составляют ±0,3 г и по большей части вызваны ограничением точности датчика температуры. Видно, что основное замерзание раствора заканчивается при –4,5оС. После этого процесс если и продолжается, то он трудно отличим от погрешности измерений и захватывает не более 1 грамма (2%) вещества. ЗАКЛЮЧЕНИЕ (ВЫВОДЫ) 1. Разработана методика проведения эксперимента по определению температуры кристаллизации влаги в материале кирпича. Значимость данной методики определяется в первую очередь тем, что она позволяет исследовать процесс кристаллизации при значительной разнице масс твердой и жидкой фаз. Эксперимент разработан с учетом возможности его проведения с использованием доступного лабораторного оборудования. 2. При разработке методики применен новый подход, который определяет изучение процесса кристаллизации воды из раствора при условии образования нановеществ в виде гидратов солей. Влага 3. Разработана математическая методика обработки результатов эксперимента. Результаты анализа, проведенные с использованием разработанной методики, показали высокую достоверность результатов. Погрешность расчетов не превышает 1%. 4. Анализ разработанной методики позволяет выявить направление увеличения точности расчетов. 5. Применение разработанных лабораторного эксперимента и математической методики позволяют определить важные для теплотехнических расчетов и расчетов долговечности материалов значения количества незамерзшей воды в материале, температуры начала и конца кристаллизации влаги в кирпиче, концентрацию электролита во влаге, а также доказать принципиальный механизм поведения влаги в материале кирпича с точки зрения физикохимических процессов. 6. Возможность определения концентрации солей в растворе создает условия для разработки нанотехнологий управления процессом замерзания влаги в ограждающих конструкциях на основе изменения исходного состава материала. в материале рассматривается как эвтектический раствор, полученный в процессе гидратации некоторых оксидов и солей, входящий в состав материала.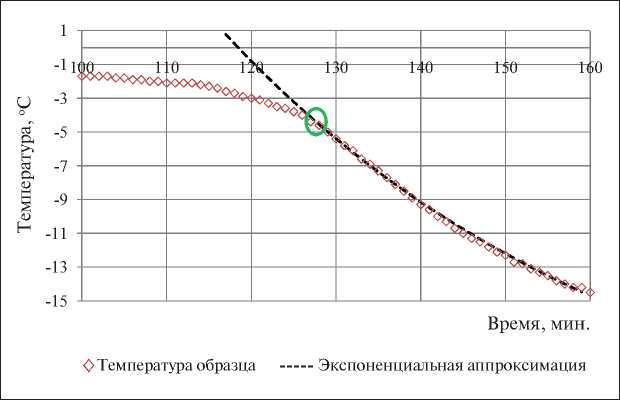
Список литературы Исследование процесса кристаллизации влаги в кирпиче
- Фокин К.Ф.Строительная теплотехника ограждающих частей зданий. - М: АВОК-ПРЕСС, 2006. - 256 с.
- Gagarin V.G. Thermal performance as the main factor of energy saving of buildings in Russia // Procedia Engineering "8th International Cold Climate HVAC 2015 Conference". - Dailan: Elsevier, 2016. - Р. 112-119.
- Gagarin V., Akhmetov V., Zubarev K. Assessment of enclosing structure moisture regime using moisture potential theory // MATEC Web of Conferences. - Ho Chi Minh City: EDP Science, 2018. - P. 3053.
- Коновалов В.В. Общие закономерности развития экогеосистем (деформационная модель). - Saarbrucken: Palmarium academic publishing, 2012. - 252 с.
- Bermejo-Pareja F., Benito-Leon J., Vega S. at al. Incidence and subtypes of dementia in three elderly populations of centralSpain // J. Neurol. Sci. - 2008. - V. 264. - P. 63-72.
- Желдаков Д.Ю. Методы исследования кинетики процесса химической коррозии материалов кирпичной кладки // Известия высших учебных заведений. Строительство. - 2019. - № 11. - С. 74-86.
- Mirnik M. Electrostatic and chemical interactions of ions in electrolytes and in ionic point-charge double layers II // Progress in Colloid and Polymer Science. - 2000. - V. 115. - P. 334-341. 10.1007/3-540-46545 6 64.
- DOI: 10.1007/3-540-46545664
- Properties of porous silicon / Ed. by L. Canham. - London: EMIS Datareviews. Ser. №.18, 1997. - 400 p.
- Желдаков Д.Ю. Химическая коррозия кирпичной кладки. Протекание процесса // Строительные материалы. - 2019. - № 4. - С. 36-43.
- Butterworth B., Baldwin L.W. Laboratory test and the durability of brick: The indirect appraisal of durability (continued) // Transactions of the British Ceramics Society. - 1964. - №. 63(11). - Р. 647-661.
- Orlovich R.B., Nowak R., Vatin N.I., Bespalov V.V. Strength evaluation of the Prussian vaults made from brick aggregate concrete // Magazine of Civil Engineering. - 2018. - №. 82(6). - Р. 95-102.
- DOI: 10.18720/MCE.82.9
- Bespalov V., Orlovich R., Zimin S. Stress-strain state of brick masonry vault with an aperture // MATEC Web of Conferences. - 2016. - №. 53. Art. no. 01009.
- DOI: 10.1051/matecconf/20165301009
- Franchi A., Crespi P., Ronca P., Pizzamiglio F. An in situ diagonal compression test for brick walls with displacement control on the two external layers // International Journal for Housing Science and Its Applications. - 2014. - №. 38(1). - Р. 25-35.
- Loganina V.I., Skachkov Y.P., Lesovik V.S. Quality control of building materials according to uncertainty of measurement and stability of the technological process of production. No. 1161. P. 86-97. 10.4028/www. scientific.net/SSP.299.1161.
- DOI: 10.4028/www.scientific.net/SSP.299.1161
- Perovskaya K., Petrina D., Pikalov E., Selivanov O. Polymer waste as a combustible additive for wall ceramics production // E3S Web of Conferences. - 2019. - №. 91. Art. no. 04007.
- DOI: 10.1051/e3sconf/20199104007
- Vitkalova I., Torlova A., Pikalov E., Selivanov O. Development of environmentally safe acid-resistant ceramics using heavy metals containing waste // MATEC Web of Conferences. - 2018. - №. 193. - Art. no. 03035.


