Исследование процесса пробития алюминиевых преград сферическим ударником в диапазоне от 460 до 700 м/с

Процессы, протекающие в твердых телах при динамических нагрузках, являются предметом фундаментальных и прикладных исследований во всем мире. В работах [1–5] приведены последние достижения в области физического и математического моделирования процессов пробития и проникания ударников в конструкции из перспективных материалов. Там же указаны границы применимости аналитических методов и представлены верифицированные аналитические зависимости для расчета ударной стойкости конструкций и пробивного действия ударников. Несмотря на все многообразие методик моделирования, все еще актуальным является разработка и модификация уже имеющихся численных методов путем усовершенствования алгоритмов расчетов, критериев разрушения и т. п.

Обзор научно-технической и патентной литературы в настоящее время показывает, что как у нас в стране, так и за рубежом малоизученными являются вопросы динамики деформирования и разрушения материалов при действии ударных и ударно-волновых нагрузок. Основное достоинство развиваемого авторами подхода заключается в том, что он позволяет проследить по времени процесс деформирования и разрушения материала, а также иметь полную информацию о напряженно-деформированном и термодинамическом состоянии элементов конструкции в любой момент времени. Для задач соударения представляется возможным получить во времени всю картину внедрения, пробития и образования осколков с учетом ударно-волнового характера деформирования и разрушения как материала ударника, так и преграды.

В работах [6–7] классифицированы многослойные преграды и показано, что в некоторых случаях они обладали большей ударной стойкостью, чем монолитные. Проявлялась зависимость от типа ударника, его носовой части и начальной скорости, а также угла соударения. Авторы от- мечают, что, по-видимому, такие металлы, как алюминий и сталь еще долго будут играть роль основных материалов в защитных конструкциях. Использование модифицированного лагранжева подхода в настоящее время представляет определенный интерес с точки зрения расширения научных знаний и определения границ его применимости. В дополнение к проведенным исследованиям ниже изучено влияние двукратного увеличения прочностных характеристик алюминиевых преград на процесс пробития их стальным сферическим ударником при скоростях от 460 до 700 м/с.

Такой диапазон прочностных характеристик выбран в связи с возможностью достижения указанных значений в практике разработки перспективных материалов. При этом математическое моделирование процесса соударения играет важную роль для оценки результатов прогнозирования свойств создаваемых материалов.

Математическая модель и численный метод расчетов

Поведение материалов описано с позиций феноменологической макроскопической теории механики сплошных сред. Материал моделируется пористой, сжимаемой, упруго-пластической средой с учетом свойств прочности и ударно-волновых явлений. Определяющие соотношения задаются уравнениями Прандтля–Рейса при условии текучести Мизеса. При описании разрушений используется детерминированный подход, в рамках которого в материалах образуются разрушения по типу сдвига и по типу отрыва. Это достигается одновременным учетом нескольких критериев разрушения. С точки зрения авторов, это позволяет моделировать ударно-волновые процессы в твердых телах наиболее приближенно к реальным [8].

В качестве основного инструмента исследований использовался численный лагранжев метод, расчетная часть которого дополнена механизмами расщепления расчетных узлов и разрушения расчетных элементов. Согласно терминологии [4], метод содержит оригинальный способ выделения поверхностей разрыва сплошности материалов, который не накладывает серьезных ограничений на решение пространственных задач пробития и проникания. Одним из достоинств метода является возможность моделирования процессов сквозного пробития и глубокого внедрения ударников сложной геометрии из различных материалов. Расчеты проведены некоммерческом программном комплексе «Удар.Ос.2», разработанном в Томском государственном университете [9]. Программный комплекс, выполненный на языке Си++, содержит программы подготовки данных, решатель и просмотрщик.

Тестовые расчеты

Достоверность результатов численного моделирования установлена путем решения ряда тестовых задач. Вначале результаты сравнивались с аналитическим решением Ренкина–Гюгонио. Далее численные результаты сопоставлялись с экспериментальными данными, в том числе по величине запреградной скорости ударника, глубины его внедрения и диаметров пробоины (входной и выходной диаметр), относительного укорочения ударников и т. п. Наконец, численные результаты сравнивались с результатами, полученными другими исследователями в части определения доминирующего механизма разрушения и пробития.

Анализ чувствительности сетки

На начальном этапе тестовых расчетов был проведен анализ чувствительности расчетной сетки. Анализ проведен с целью достижения консервативного результата, включая морфологию разрушения, характера баллистических кривых, а также значений некоторых интегральных характеристик процесса взаимодействия. Как показано в [10], это является важнейшим этапом верификации алгоритмов расчетов. Всего было построено три конечно-элементные модели взаимодействующих тел, отличающиеся количеством элементов в преграде. Рассмотрены конечноэлементные модели с частой разбивкой (модель 1), средней (модель 2) и редкой (модель 3). Количество элементов варьировалась от 5 000 до 10 000, использовался трехузловой элемент типа «равнобедренный треугольник». В автоматическом режиме было сделано сгущение элементов в преграде в области, приблизительно равной трем радиусам ударника. При расположении области сгущения элементов авторы ориентировались на экспериментальные результаты из [6].

На рис. 1 показаны результаты, полученные по всем трем моделям. Видно, что характер баллистических кривых и морфология разрушения преград были схожи. На временных кривых ско-

Механика

рости отчетливо видны интервалы ее быстрого (до 15 мкс) и медленного (с 15 мкс) снижения. Кривые скорости отражали также установившееся движение ударника и, как следствие, выход его из преграды. В морфологии разрушения также не обнаружено значительных различий, а именно, отсутствие пластической деформации ударника и сильно поврежденная выбитая алюминиевая пробка. Размер осколков зависел от размера триангуляционных элементов в преграде, но в обоих случаях соответствовал экспериментальным данным.

Профили скорости свободной поверхности приведены на рис. 1. Отчетливо видно, что по- следняя конечно-элементная модель не выявила осцилляций на кривых после выхода ударной волны на свободную поверхность. Скорее всего, на наличие осцилляций на графике влияло состояние выбитой откольной тарелки, которая во всех трех случаях была сильно разрушена. В целом профили скорости свободной поверхности близки к экспериментальным. Сопоставляя полученные результаты с экспериментальными и учитывая морфологические особенности процесса разрушения и затраченное время счета, выбрали конечноэлементную модель 2. В данном случае консервативный результат достигался в случае, когда размер элемента в преграде был почти в два раза меньше, чем в ударнике, при этом область сгущения в преграде составляла не менее трех радиусов ударника.

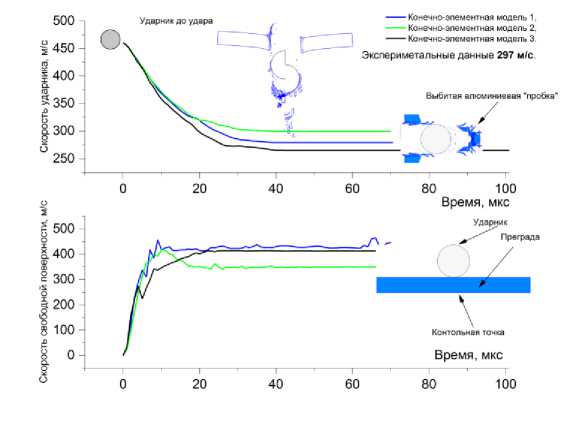
Рис. 1. Расчеты процесса пробития преграды из Д16 стальным шариком со скоростью 460 м/с

Ударник и объекты исследования

Объектом исследования выбрана однородная пластина из сплава Д16 размерами 60×6 мм в продольном сечении. В работе изучено влияние увеличения прочностных характеристик пластины при взаимодействии со стальным шариком диаметром 12,7 мм в диапазоне от 460 до 700 м/с. Материалом шарика была упрочненная сталь ШХ15.

Рассмотрены пластины с увеличенными в два раза относительного исходного варианта критическими значениями предела текучести, откольной прочности и удельной работы сдвиговых пластических деформаций. Две последние величины являются критериями разрушения материала, отвечающими за образование отрывных и сдвиговых разрушений соответственно. Таким образом, серия вычислительных экспериментов состояла из восьми вариантов. Для удобства введены обозначения образцов как (пр. тек. × 2), (отк. проч. × 2) и (сдвиг. проч. × 2), соответственно.

Физико-механические характеристики исходного образца были следующие: начальная плотность 2,78 г/см3, объемная скорость звука 5380 м/с, модуль сдвига 25,8 ГПа, эквивалентная пластическая деформация 1,2, предел текучести 0,42 ГПа, откольная прочность 0,5 ГПа, удельная работа сдвиговых пластических деформаций 35 кДж/кг.

Исследование процесса пробития базовых и упрочненных алюминиевых преград стальным ударником при 460 и 700 м/с

Влияние двукратного увеличения предела текучести материала преграды на процесс пробития

Вначале изучено влияние двукратного увеличения предела текучести материала преграды на процесс ее пробития. На основе численных результатов был воспроизведен сценарий разрушения исходных преград и преград с завышенным значением предела текучести. Для выявления основных различий процесс пробития преград при 460 м/с условно был разделен на стадии и детально проанализирован. Предел текучести исходного материала равен 0,42 Гпа.

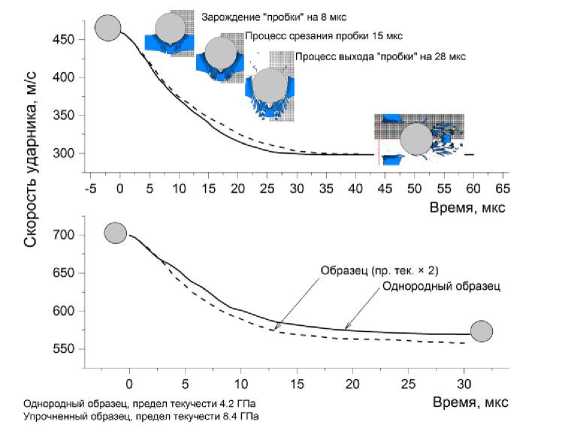
На первой стадии отмечается пластическая деформация преграды (выход фронта пластической деформации на тыльную поверхность), на второй и третьей стадии формировалась «пробка» в преграде, на четвертой и пятой полностью образовавшаяся «пробка» выбивалась из преграды. Фрагменты конфигураций «ударник–мишень» соответствующие некоторым стадиям пробития изображены на рис. 2.

В однородной преграде первая стадия длилась не более 8 мкс, при этом зарождение будущей пробки там завершилось уже к 12-й мкс. Полностью сформировавшаяся пробка диаметром почти 10 мм начинает выходить из преграды на 15-й мкс, что сопровождается ее дальнейшим разрушением и формированием облака лидирующих осколков. С 28-й по 44-ю мкс фиксировался выход ударника, при этом его задняя часть достигала тыльной поверхности преграды на 65-й мкс, что соответствовало окончательному выходу из преграды. Скорость шарика после пробития преграды составила 299 м/с. В эксперименте ее значение равнялось 313 м/с. На верхнем графике штрихпунктиром показана кривая скорости для усиленного образца, имеющая незначительные отличия от кривой скорости для однородного образца. Расчетным путем установлено, что после пробития усиленного образца скорость ударника составляла 297 м/с.

Итак, сравнение баллистических кривых для скорости 460 м/с показало, что кривые совпадали только на первой и последней стадиях, расхождение между ними было только в середине про- цесса.

С увеличением начальной скорости ударника было установлено, что серьезных различий об- наружено не было. В обоих случаях ударник не теряет своей первоначальной формы, выбивая из преграды сильно разрушенную пробку. Как показывают расчеты, диаметр пробки несколько меньше исходного диаметра ударника, а края пробоины разрушены. Все очаги разрушения сосредоточены возле нее, радиальных трещин, распространяющихся от края пробоины к тыльной боковой поверхности, не обнаружено. Основным отличием можно считать размер внутреннего диаметра пробоины. Получено, что скорости ударника после пробития однородного и усиленного образцов почти совпадали и составили 569 и 558 м/с соответственно. При этом баллистические кривые для этих вариантов расчетов полностью совпадали только на начальной стадии пробития.

Образец (пр. тек * 2)

, Однородный образец го

0       5      10

Однородный образец, предел текучести 4.2 ГПа

Упрочненный образец, предел текучести 8 4 ГПа

25     30

Время, мкс

Зарождение "пробки" на 8 мкс

. я»щпрснесс срезания пробки -5 мкс к А ' Процесс выхода "лообки" на 28 мкс

-5 0   5 10 15 20 25 30 35 40 45 50 55 60 65

Время, мкс

Рис. 2. Результаты расчетов процесса пробития базовой алюминиевой и алюминиевой преграды с удвоенным значением предела текучести

Влияние двукратного увеличения откольной прочности материала преграды на процесс пробития

Далее изучено влияние двукратного увеличения откольной прочности в материале преграды на процесс ее пробития. В данном случае, рассмотренная величина является одном из критериев разрушения в используемой модели. Очевидно, что образец будет больше сопротивляться от-кольным разрушениям. Откольная прочность исходного материала равна 0,5 ГПа.

Воспроизводя процесс пробития однородных и усиленных откольной прочностью преград, существенных отличий не обнаружили. Преграды были насквозь пробиты шариком без его пластической деформации. Все разрушения сконцентрированы по краям пробоины, а из преграды была выбита «пробка», которая в зависимости от скорости имела разрушения средней и сильной степени.

Для проведения сравнительного анализа все баллистические кривые были расположены на одном графике на рис. 3. По аналогии с предыдущем случаем вверху были представлены расчетные кривые для скорости 460 м/с, а внизу - для скорости 700 м/с. Видно, что баллистические

Механика

кривые для базового и усиленного откольной прочностью образцов практически полностью совпадали. При этом совпадения с кривой относящейся к образцу с усиленным значением предела текучести, имели место только на начальных и конечных стадиях процесса пробития. Установлено, что при скорости ударника 460 м/с его запреградная скорость равнялась 300 м/с и практиче ски полностью совпадала с предыдущими рассчитанными значениями.

При начальной скорости ударника, равной 700 м/с, наблюдалась похожая картина. Однако

все три баллистические кривые совпадали только на начальной стадии, а на конечной стадии они становились параллельными друг другу. Что касается баллистических кривых для усиленных образцов, то они совпадали еще и в середине процесса до 8 мкс включительно. Таким образом, ударная стойкость образца с завышенным значением от-кольной прочности была выше, чем однородного образца и образца с завышенным значением предела текучести. Однако, судя по рассчитанному значению запреградной скорости, равной 554 м/с, весьма незначительно. Полученные результаты являются предсказуемыми и объясняются тем, что в процессе пробития откольное разрушение не являлось доминирующим.

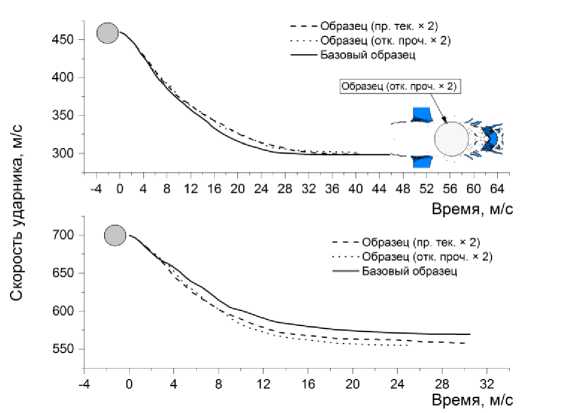
Рис. 3. Результаты расчетов процесса пробития базовой алюминиевой и алюминиевой преграды с удвоенным значением откольной прочности

Влияние двукратного увеличения удельной работы сдвиговой пластической деформации преграды на процесс пробития

В завершение проанализируем процесс пробития преград с удвоенным значением сдвиговой прочности. Согласно логике проводимых исследований, данный образец должен больше сопротивляться сдвигу. Однако расчеты показали, что все преграды были пробиты ударником насквозь без заметной пластической деформации по уже вышеописанному механизму. Время процесса пробития незначительно отличалось от времени пробития однородного образца, а состояние выбитой пробки можно охарактеризовать как средней степени разрушения.

Баллистические кривые для всех рассмотренных образцов приведены на рис. 4. Видно, что все кривые совпадали только на начальной стадии пробития, причем при скорости 460 м/с этот период был в два раза дольше и составил почти 8 мкс. Нетрудно заметить, что кривые скорости упрочненного сдвиговой прочностью образца расположены ниже остальных. Таким образом, можно утверждать в процессе пробития доминировал сдвиговой механизм, «пробка» как бы срезалась под действием ударника, однако сам образец не смог его остановить.

При начальной скорости ударника 460 м/с его запреградная скорость составляла 253 м/с, что явля-

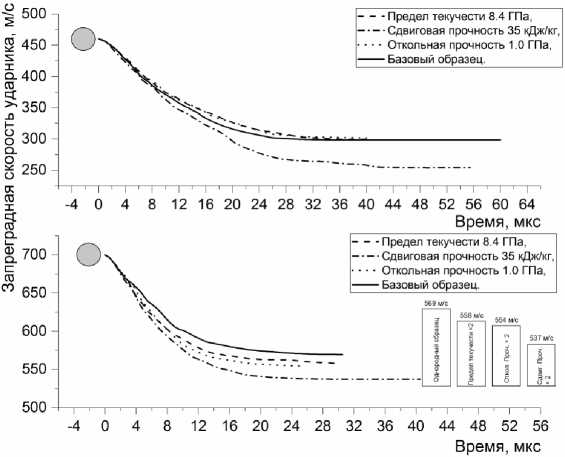
Рис. 4. Результаты расчетов процесса пробития базовой алюминиевой и алюминиевой преграды с удвоенным значением сдвиговой прочности

лось минимальным значением и на 15 % меньше скорости, зафиксированной в варианте расчетов базового образца. При начальной скорости 700 м/с также получено минимальное значение, равное 537 м/с. Однако расхождение с базовым образцом здесь уменьшилось до 5 %.

Результаты расчетов

В таблице представлены результаты расчетов для всех рассмотренных вариантов. Результаты дают количественное и качественное представление о процессе пробития базового алюминиевого и упрочненных образцов при скоростях 460 и 700 м/с. В таблице приведены начальная скорость ударника, время пробития (момент полного его выхода из преграды), запреградная скорость ударника (скорость его центра масс), величины входного и выходного диаметров пробоины и энергии поглощения ударника. Кроме того, качественно оценено состояние выбитой из преграды «пробки».

Установлено, что упрочнение образцов одной из выбранных прочностных характеристик во всех случаях приводило к повышению ударной стойкости преграды по сравнению с базовым образцом. Это выражалось в уменьшении запреградной скорости ударника, в незначительном увеличении времени процесса пробития и в увеличении выходного диаметры пробоины. Других значимых отличий в морфологии разрушения образцов обнаружено не было. При этом ударник насквозь пробивал все преграды, не теряя своей исходной сферической формы.

Путем прямого сравнения получено, что при скорости 460 м/с наибольшей ударной стойкостью обладал образец с увеличенным значением сдвиговой прочности. После пробития этого упрочненного образца запреградная скорость ударника составила 253 м/с, что почти на 15 % меньше, чем после пробития базового. После пробития образцов с завышенными значениями отколь-ной прочности и предела текучести отмечено незначительное расхождение в расчетных значениях. Запреградные скорости в этих вариантах были меньше на 2,6 и 1,7 % соответственно. Такая же тенденция сохранилась при начальной скорости 700 м/с, однако расхождение в запреградных скоростях уменьшилось до 5 %.

Установлено, что упрочнение образцов слабо влияло на время процесса пробития. Так, при скорости 460 м/с время пробития получилось от 69 до 73 мкс, а при скорости 700 м/с – от 37 до 40 мкс. Время пробития рассчитывалось как время полного выхода ударника из преград.

Расчетным путем было установлено, что в некоторых усиленных образцах с тыльной стороны вблизи пробоины выбивался дополнительный осколок. С точки зрения авторов, данный факт говорил о том, что образец сильнее сопротивлялся пробитию. Наиболее разрушенные края пробоины наблюдались после пробития базового образца. Установлено, что во всех усиленных образцах выходной диаметр пробоины был больше, чем выходной диаметр, наблюдаемый после пробития базового образца. Наибольшие диаметры выходных пробоин обнаружены в образцах с увеличенным значением предела текучести и удельной работы сдвиговых пластических деформаций.

Установлено, что при пробитии базового образца при скоростях 460 и 700 м/с поглощалось энергии 510 и 698 Дж соответственно. При пробитии образцов с увеличенным значением сдвиговой прочности эти затраты энергии увеличивались до 619 и 846 Дж. В образцах с увеличенным значением откольной прочности отмечен средний уровень разрушения выбитой «пробки». В данном случае вместо алюминиевых осколков наблюдался фрагмент преграды в виде выбитой «пробки».

Заключение

На основании полученных результатов были сделаны следующие выводы. В целом характер баллистических кривых, морфология разрушения преград и механизм пробития были примерно одинаковыми как для базовой преграды, так и для всех упрочненных образцов. В рассмотренном диапазоне скоростей сферический ударник не деформировался пластически, и выбивал из преграды «пробку». Разрушения «пробки» можно охарактеризовать как средние (фрагмент выбитой пробки и осколки) и высокие (только осколки алюминия).

Наибольшее сопротивление пробитию оказывали преграды с увеличенным значением сдвиговой прочности. В этих вариантах расчетов отмечено незначительное увеличение времени пробития и уменьшение запреградной скорости ударника. Баллистические кривые практически совпадали с баллистической кривой для базового образца. Основное различие было в наличие совпадений кривых вначале и конце процесса пробития.

Механика

Результаты расчетов процесса пробития алюминиевых преград

Преграда Исходный образец обозначался как Д16, в обозначении упрочненного образца стоял символ «×2)»	о о о О о И Я се К	о X ю О о и к	о о (Я К се о	Диаметр пробоины, мм		Энергия поглощения, Дж	НН НН со о се н СО ~ Л зЯ Я Я я
				X со	Й О И о X м
Преграда исходная Д16	460	69	300	13	13,4	510	Высокий
Пр-да Д16 (пр. тек. × 2)	460	73	299	14,5	14,24	513	Средний
Преграда исходная Д16	700	37	569	14,2	14,3	698	Высокий
Пр-да Д16 (пр. тек. × 2)	700	40	558	14,1	14,9	750	Средний
Пр-да (Отк.проч × 2)	460	69	301	13,4	13,3	509	Средний
Пр-да (Отк.проч. × 2)	700	39	554	13,1	13,7	768	Средний
Пр-да Д16 (сд. проч× 2)	460	71	253	13,2	12,7	619	Средний
Пр-да Д16 (сд. проч× 2)	700	39	537	13,3	13,6	846	Высокий

Скорее всего, откольная прочность и предел текучести также влияли на процесс взаимодействия, но только в другом интервале начальных скоростей, возможно, ниже предела сквозного пробития.

Созданные средства математического моделирования могут быть полезны при проведении фундаментальных и прикладных исследований. Предложенный подход позволяет выяснять механизмы и закономерности процесса высокоскоростного деформирования и разрушения конструкционных материалов и, кроме того, получать результаты в недоступной для эксперимента области начальных условий. При проведении комплексного рационального проектирования реализуется возможность прогнозирования поведения перспективных ударостойких защит различных объектов и техники для облегчения поиска оптимального варианта защитной конструкции.

Исследование выполнено за счет гранта Российского научного фонда № 23-29-00257,