Исследование процессов переупаковки клеток в эпителиальных листах in silico. Часть I. Одноосное растяжение ткани

RUSSIAN JOURNAL OF BIOMECHANICS

Научный интерес к исследованиям по поведению многоклеточных тканей методами in silico не угасает.

Об этом можно судить по работам, которые выходят из года в год по данному направлению [1–7]. Это связано с тем, что, используя компьютерные технологии, возможно проводить исследования без вреда для реальных

0000-0002-2629-521X

0009-0002-5969-6893

Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International

License (CC BY-NC 4.0)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

живых тканей и организмов. Кроме этого, математическое моделирование позволяет проследить эволюционную динамику всей многоклеточной ткани, что в некоторой степени ограничивает экспериментальные методы исследования.

Переупаковка клеток – это важный процесс при развитии тканей, особенно в эпителиальных тканях. Эпителиальные клетки образуют сплошной слой, который выстилает поверхности органов и полостей тела. Переупаковка клеток играет ключевую роль в том, как такие ткани развиваются, восстанавливаются и приспосабливаются к изменениям [8]. Становится ясно, что процессы переупаковки клеток, возникающие при ремоделировании тканей, способствуют адаптации клеток к изменениям при механической нагрузке или воздействии со стороны внешней среды. При этом клетки могут изменять свою форму и взаиморасположение, чтобы оптимально распределить нагрузку либо реагировать на другие внешние стимулы. Также переупаковка клеток способствует их механической интеграции [9]. Эпителиальные клетки соединены плотными контактами и десмосомами, что обеспечивает тканям механическую прочность. Переупаковка клеток сопровождается перестройкой этих контактов. Благодаря этому эпителиальные ткани остаются устойчивыми к деформациям и поддерживают целостность при изменении формы или при росте. Также в случае повреждения эпителия возникающие процессы регенерации сопровождаются переупаковкой клеток [8]. Клетки эпителия на границе раны могут растягиваться, делиться и замещать погибшие клетки, одновременно поддерживая структурные связи с окружающими клетками. Таким образом, переупаковка способствует быстрому закрытию повреждённых участков и восстановлению барьерных функций. При морфогенезе на ранних этапах развития эмбриона (от дробления до нейруляции) клетки эпителия переупаковываются, что формирует структуры будущих органов [9; 10]. Таким образом, процессы переупаковки клеток при развитии эпителиальных тканей имеют важное значение.

Использование методов живой микроскопии, лазерной абляции и атомно-силовой микроскопии позволило детально исследовать, как клетки реагируют на механические стимулы и какие молекулы участвуют в этих процессах [11–14]. Эти методы также помогли изучить эпителиально-мезенхимальный переход (ЭМП) [15; 16], важный для миграции клеток в рамках ремоделирования тканей или опухолевых процессов [16; 17]. В контексте онкологии переупаковка клеток играет ключевую роль в метастазировании – процессе, при котором клетки опухоли теряют свои адгезивные свойства и приобретают подвижность. Этот процесс пока изучен недостаточно, и это является одним из важных направлений исследований для разработки методов борьбы с онкозаболеваниями. Переупаковка клеток при заживлении ран – это активная тема исследований. Ученые обнаружили ключевые молекулы [18; 19], такие как

TGF -β, которые регулируют процесс миграции клеток, чтобы закрыть повреждения. Изучение заживления ран с помощью in vivo моделей показало, что клетки могут не только мигрировать, но и активно перестраиваться, сохраняя при этом прочные клеточные связи.

Однако, несмотря на значительный прогресс, многие аспекты процессов клеточной переупаковки до сих пор остаются неясными, так как они сложны и многогранны. Переупаковка клеток может отличаться в зависимости от типа ткани, стадии развития или наличия патологий. Понимание этих контекстных различий требует более глубоких исследований. А применение полученных знаний для разработки новых методов лечения заболеваний, связанных с нарушениями эпителиальной ткани (например, рака, фиброза), требует дополнительных исследований.

Применение математических моделей и компьютерных симуляций к процессам клеточной переупаковки является мощным инструментом, особенно в последнее десятилетие. Математические модели позволяют предсказать, как клетки будут вести себя в ответ на изменения внутренней или окружающей среды, или генетические мутации. Симуляции могут моделировать сложные процессы, такие как переход клеток из одного состояния в другое [20], рост злокачественных образований [21; 22], заживление ран [23; 24], начальные стадии морфогенеза [25–27], образование регулярных клеточных сеток [28–30].

Для разработки математических моделей эволюции тканей применяются два подхода: континуальный и дискретный. Несмотря на то, что континуальный подход был разработан давно, он всё ещё остаётся актуальным и широко применяется при математическом моделировании развития многоклеточных тканей [3; 31; 32]. Однако, несмотря на свою простоту и широкую распространённость, этот подход уступает дискретному в том, что не позволяет учитывать индивидуальную динамику элементов системы. В контексте многоклеточной ткани таким элементом является клетка. Учёт всех изменений, происходящих с клеткой, важен, так как они определяют полную картину эволюции живой материи. В рамках дискретного подхода выделяют клеточные автоматы [33], модель Поттса [2], модели молекулярной динамики [34] и вершинные модели [29; 30].

На наш взгляд, последний является наиболее подходящим для математического моделирования поведения эпителиальных тканей. Это связано с двумя ключевыми аспектами. Во-первых, этот метод позволяет достаточно точно описать элементарную единицу живой материи – клетку. В рамках данного подхода клетка представлена в виде многоугольника, который динамически изменяет свою форму и размеры при взаимодействии с другими клетками. Взаимодействие этих клеток в ансамбле формирует эпителиальную ткань, где клетки плотно прилегают друг к другу. Во-вторых, этот метод пользуется широкой популярностью для моделирования эпителиальных тканей [1; 7; 23; 26; 35–38]. Значитель- ное преимущество этого подхода заключается в том, что взаимодействия элементов системы определяет потенциал, составляющие которого легко интерпретируются с физической точки зрения. В недавнем обзоре [37] подробно рассмотрены преимущества этого подхода по сравнению с другими, такими как континуальные модели, клеточные автоматы и методы молекулярной динамики.

Что касается работ по математическому моделированию переупаковки клеток в эпителиальных тканях, то такие встречаются достаточно редко. В работе [39] авторы с использованием вершинной математической модели исследовали процессы интеркаляции в эпителиальных тканях. Было получено удовлетворительное соответствие результатов моделирования с экспериментальными данными. Результаты работы демонстрируют, что координация процессов интеркаляции зависит от когерентности в локальных конфигурациях натяжения, количественно определяемых определённым параметром порядка в пространстве натяжения. С помощью представленной модели были воспроизведены существенные особенности удлинения зародышевой полосы в масштабе ткани и клеток во время гаструляции Drosophila, в частности замедление потока ткани после приблизительно двукратного расширения, сопровождающееся потерей порядка в конфигурациях натяжения. В другой недавней работе [40] авторы представили математическую модель развития эпителиальных листов. При разработке модели был использован подход episcale [41]. Такой подход описывает клетку из набора частиц, которые составляют её внешнюю оболочку и внутреннюю часть. Данный подход напоминает комбинацию методов молекулярной динамики и вершинную модель. Необходимо прописывать потенциал взаимодействия для всех частиц, внутренних и внешних. Это усложняет разработку модели, но позволяет описывать клетку на различных пространственных масштабах. Сравнивая результаты моделирования работ [40; 41] с работой [29], где при моделировании используется классическая вершинная модель, можно заключить, что результаты моделирования качественно и количественно соответствуют друг другу. Интересно отметить, что клеточная сетка с клетками-пузырями также наблюдается в работе [40], образование которой подробно описано с физической точки зрения в работе [29]. Но при этом в работе [29] используется классическая вершинная математическая модель. Это показывает, что моделирование процессов в многоклеточной ткани более сложным методом episcale избыточно. Также есть и немногие другие работы, в которых используют вершинную математическую модель при исследовании процессов переупаковки клеток. Например, в работе по моделированию переупаковки клеток ткани [28] наблюдалось образование различных клеточных сеток в процессе ремоделирования зрелых эпителиальных тканей вследствие хемомеханических взаимодействий. В работе авторами рассмотрено взаимодействие клеток без учёта их способности к самовоспроизведению путём деления.

Мы продолжаем развивать предложенную нами ранее математическую модель [21; 22; 26; 29] на случай исследования переупаковки клеток при развитии эпителиальной ткани. В данной работе с её помощью мы исследуем влияние механизмов переупаковки клеток на развивающуюся эпителиальную ткань. Особое внимание при моделировании мы уделяем структурной единице многоклеточной ткани, клетке как элементу большой сложной системы. Модель включает в себя реальные процессы развития живой ткани, такие как деление и интеркаляция клеток, обмен химическими и механическими сигналами, а также клеточные процессы синтеза белков. Процесс деления клетки в модели реализован таким образом, что является симметричным, как это зачастую происходит в реальных здоровых тканях. Помимо этого, разработанная модель отличается от упомянутых выше потенциалом взаимодействия. Введённый нами потенциал учитывает не только эластичность периметра и площади, а также и эластичность внутренних углов клетки. Разработанная математическая модель в полном виде описана в разделе «Математическая модель». Численное исследование переупаковки клеток при одноосном растяжении многоклеточной ткани представлено в разделе «Результаты математического моделирования». В разделе «Заключение» приведены дальнейшие перспективы развития математической модели, обсуждены перспективы применения результатов и приведены выводы.

Математическая модель

Перед моделированием процессов переупаковки клеток в эпителиальной ткани следует рассмотреть её строение. Эпителиальная ткань представляет собой совокупность полярных дифференцированных клеток, плотно прилегающих друг к другу и образующих пласт, который расположен на базальной мембране. Эпителий выполняет барьерную функцию на границе внешней или внутренней среды организма и составляет большую часть желез. Например, эпителий покрывает поверхность кожи, роговицу глаза, серозные оболочки, а также выстилает внутреннюю поверхность полых органов пищеварительной, дыхательной и мочеполовой систем. В эпителиальной ткани отсутствует межклеточное вещество, а клетки эпителия образуют непрерывный пласт, получающий питание через базальную мембрану. Клетки связаны друг с другом молекулами адгезии вдоль общих границ и взаимодействуют как друг с другом, так и с окружающей средой. Эти сложные взаимодействия могут вызывать значительные морфогенетические изменения развивающихся тканей, такие как складки, растяжения или сужения, что играет ключевую роль в формировании многоклеточного организма. Понимание механизмов коллективного поведения клеток при решении данной задачи является важным аспектом на пересечении физики, химии, биологии развития и компьютерных технологий. Важно отметить, что клетки эпителия не способны к свободному перемещению, что определяет их фенотип как эпителиальный [42]. Это означает, что их поведение полностью контролируется тканью. Противоположным является мезенхимальный фенотип, при котором клетки могут перемещаться свободно [42]. Такое поведение характерно, например, для раковых клеток [17], которые не подчиняются системным сигналам ткани. Здоровые клетки эпителиального фенотипа также могут временно переходить к мезенхимальному фенотипу, например, в процессе заживления раны. Внутренние клеточные напряжения в эпителии генерируют силы, которые изменяют форму клеток. Цитоскелет играет ключевую роль в создании этих напряжений [43]. Актиновая кора, в частности, создаёт поверхностное и линейное натяжение, действующее вдоль клеточных мембран и опосредованное адгезией между клетками и внеклеточным матриксом [44; 45]. В ходе развития и в зрелом состоянии эпителиальные ткани подвергаются механическим воздействиям извне. Например, структуры, такие как базальная мембрана [46] или апикальная внеклеточная мембрана [47], могут оказывать механические ограничения на ткань.

Морфогенез является важным процессом, происходящим в ткани. Он включает изменение фенотипа клеток, деление или апоптоз клеток, а также изменение механических ограничений со стороны окружающей среды. Для понимания физики морфогенеза необходимо учитывать законы механики, согласно которым силы, действующие на ткань, должны быть уравновешены. Внутренние и внешние силы, деформирующие ткань, компенсируются силами трения или вязкими силами. Количественные физические модели тканей позволяют описать, как генерация и баланс механических сил управляют морфогенезом [48].

В нашей модели каждая клетка представлена в виде многоугольника. Существуют три типа покрытия плоскости правильными многоугольниками: треугольник, квадрат и шестиугольник [49]. Для решения нашей задачи наиболее подходящей формой клетки является правильный шестиугольник, поскольку он энергетически наиболее выгоден, будучи близок к форме окружности.

Для моделирования динамики всей системы задаётся уравнение потенциальной энергии (1). Первое слагаемое описывает эластичность площади клетки с коэффициентом упругости п, где Ai (t) - текущая площадь клетки, а A о - среднее (эталонное) значение площади, вычисляемое по формуле (2), в которой 10 длина ребра правильного шестиугольника. Значение площади Ai (t) в модели вычисляется по формуле (3), где n число

A 0       2   ¹ 0 ,

1     n ( t )

A (t) = 7 Й(xj(t) + x+(t))■(yj(t)-yj+1(t))] ,

² j = 1

вершин многоугольника, а x и y координаты, образующие стороны клетки.

Второе слагаемое в (1) описывает сократимость периметра клеток с коэффициентом ц, интерпретируемым как способность цитоскелета к сокращению. Третье слагаемое отвечает за эластичность рёбер клетки с коэффициентом о, где lij (t) - длина j-ребра i-клетки, а 10 -средняя (эталонная) длина ребра правильного шестиугольника. Четвёртое слагаемое в (1) описывает эластичность углов клетки с коэффициентом ф, aij(t) - текущее значение j-угла i-клетки в радианах, рассчитываемое по формуле аj (t) = arccos(cos(aj (t))), (4)

где cos(a ,j ( t )) определяется через скалярное произведение рёбер, образующих угол в клетке, а а₀ - среднее (эталонное) значение угла в правильном шестиугольнике (а₀ = 2п / 3). Клетки в основном имеют округлую форму, и только в определённых состояниях углы могут становиться отрицательными [50]. В связи с этим предполагается, что коэффициент ф принимает значения, строго превышающие ноль (ф > 0). Это означает, что чем больше значение φ, тем меньше отклонения угла a j ( t ) от среднего значения а₀. Таким образом, можно ограничивать эластичность клеток, чтобы избежать появления многоугольников с отрицательными углами.

N ( t )                                                                      n ( t )                                      n ( t )

U ( t ) = E n ( A ( t )^- A o ) + vP ²( t ) + ° E ( l j ( t )^{- 1} о ) + ф Е ( ^a j ( t )^{- a}o )   .

n ⁽ t )

n ⁽ t )

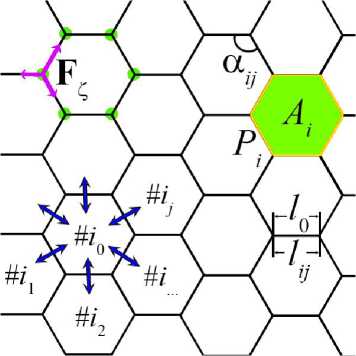
Рис. 1. Схематическое представление клеток математической модели

Ткань эволюционирует посредством перемещения вершин клеток (они отмечены зелёными точками на рис. 1). Вектор механической силы, действующей на вершину клетки (розовые стрелки на рис. 1), вычисляется стандартным образом для механики потенциальных сил как градиент со знаком минус от потенциальной энергии по радиус-вектору ζ-узла дЩЛ F =--(— z      dR?

.

Скорость перемещения клетки определяется средним арифметическим скоростей перемещения её вершин. Уравнение перемещения для вершин мы записываем в рамках механики Аристотеля, где сила определя- ет скорость

V = ^{k F} z H (I

F .l - F 0 ) .

Этот подход был выбран, поскольку клеточная ткань представляет собой сильно диссипативную среду. Это означает, что любое движение клеток происходит без эффекта инерции. Например, в работе [51] было показано, что иммунная клетка при перемещении в эпителии имеет нулевую или почти нулевую скорость, а пиковое значение скорости достигает 10 мкм/с. Также следует учитывать, что эпителиальные клетки связаны десмо-сомами и плотно прилегают друг к другу, что делает перемещение мезенхимальных клеток в эпителии затруднённым из-за низкой проницаемости среды, то есть без инерционных эффектов. Именно по этой причине уравнение движения было записано в рамках механики Аристотеля. Здесь k – коэффициент мобильности клетки, H – функция Хэвисайда, а параметр F 0 определяет критическую силу, ниже которой узел остаётся неподвижным.

Важный механизм функционирования любой живой материи – это способность к самовоспроизведению за счёт деления клеток. В модели мы вводим механизм деления клеток, который случается с распределением вероятности (7).

p div ( t ) = p о q n ⁽ t   .

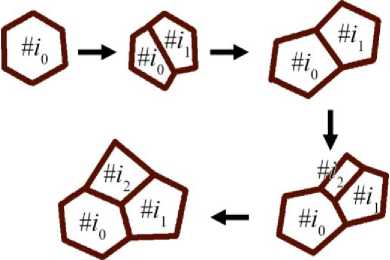
Рис. 2. Схематическое представление процесса деления клеток математической модели

Здесь p 0 и q – параметры, определяющие частоту деления клеток. Из уравнения (7) видно, что при q ≥ 1 деление наиболее вероятно для клеток, имеющих число вершин n ( t ) ≥ 6. Механизм деления в модели реализован следующим образом:

• 1)    определяется самое длинное ребро в клетке;

• 2) определяется противоположное ребро;

• 3) в центрах этих рёбер создаются новые

вершины;

• 4)    вершины соединяются новым общим ребром;

• 5)    обновляется список клеток.

Так формируется дочерняя клетка, которая включается в систему и начинает свою эволюцию с мгновенными параметрами, аналогичными материнской клетке. Такой алгоритм позволяет моделировать симметричное митотическое деление клеток (рис. 2).

Ещё один важный механизм – это интеркаляция, то есть клеточная перестройка при возникновении локальных избыточных напряжений. Она происходит, когда длина ребра l ij ( t ) между соседними клетками становится меньше критического значения d int (рис. 3). При этом общая граница между клетками поворачивается на 90^о.

Помимо механических взаимодействий клеток, в системе вводится обмен химическими сигналами. В роли химического сигнала может выступать концентрация кислорода, который необходим клеткам для поддержания их жизнедеятельности. Или процессы генной регуляции, которые зарождаются в ядре клетки, например, синтез белков семейства RhoA , которые регулируют сократимость цитоскелета. Клетки должны поглощать и перераспределять химические сигналы между соседями (синие стрелки на рис. 1). Эти процессы описываются системой уравнений:

J,(t ) = (C i (t)-Cj (t)) 8lj (t),(8)

dC (t)

- = ZJi, (t)-ec(t).(9)

dt

Первое уравнение (8) описывает межклеточную диффузию химических сигналов между соседями i -й клетки.

Здесь δ – коэффициент диффузии, а C ( t ) – вектор концентраций химических сигналов, участвующих в процессах жизнедеятельности клетки. Второе уравнение (9) описывает потребление и перераспределение этих сигналов, где суммирование потока ведётся по общему числу соседних клеток n ( t ), а β – коэффициент

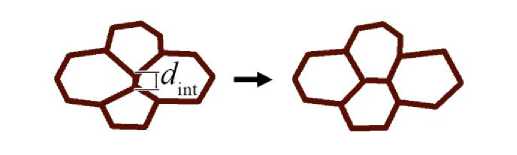
Рис. 3. Схематическое представление процесса интеркаляции клеток математической модели

деградации сигнала, интерпретируемый как скорость потребления питательного вещества или распада белковых групп.

Введение системы уравнений (8)–(9) позволяет учитывать хемомеханическое взаимодействие клеток. Это также даёт возможность описывать самый малый масштаб клеточной ткани – уровень ядра клетки, где происходят процессы генной регуляции с последующим синтезом белка. Построив несложную зависимость (10) механических параметров от химических сигналов, перед нами открывается возможность имитировать эволюцию живых тканей, которые по своей природе являются хемоэластомерами:

n = n(C(t)); ц = и(C(t)); °=°(C(t)). (10)

Разработанная математическая модель предоставляет возможность отслеживать полную историю изменений каждой клетки в рассматриваемом ансамбле. Количество клеток в модели ограничивается лишь вычислительными ресурсами. Эту модель можно классифицировать как сложную дискретную систему на основе вершинной модели. Несмотря на свою простоту, она позволяет с высокой точностью описывать динамику клеток, их деление, интеркаляцию и обмен химическими сигналами.

Результаты математического моделирования

Подробно исследован процесс переупаковки клеток в зависимости от параметра интеркаляции d int . Проведён ряд расчётов по этому параметру в диапазоне от 0,0 до 0,70 с шагом ∆ d int = 0,05. Далее будут представлены и описаны результаты моделирования по переупаковке

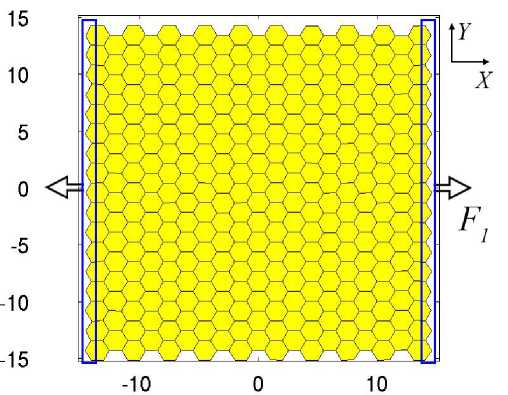
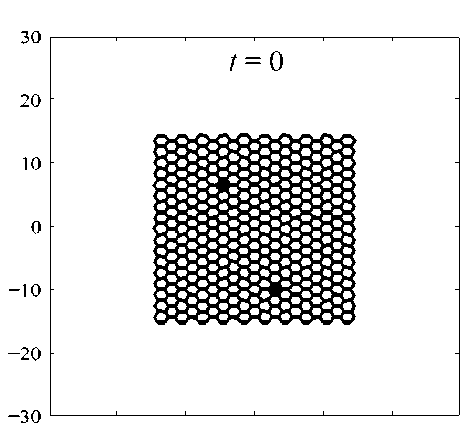
Рис. 4. Начальные условия при моделировании одноосного растяжения ткани. В синей рамке отмечены узлы клеток, на которые действует постоянная сила F1 = 0,1 вдоль оси X клеток при одноосном растяжении вдоль оси X. Начальные условия: 314 клеток расположены в центре расчётной области X (–15; 15), Y (–15; 15) (рис. 4). Верхняя и нижняя границы свободные. На узлы, которые находятся на правой и левой границах (выделено синей рамкой на рис. 4), приложена постоянная по модулю сила F1 = 0,1. На правую границу сила действует в положительном направлении, на левую – в отрицательном. Все результаты численного моделирования получены при одинаковых управляющих параметрах (таблица).

На рис. 5 и 6 представлены поля потенциальной энергии клеточной ткани. Каждое поле состоит из 16 кадров через равные промежутки времени ∆ t = 18,75. Эволюция системы занимала 300 единиц времени. Читать каждое поле нужно слева направо сверху вниз, начиная с верхнего левого угла, который соответствует кадру #1 со временем t = 0.

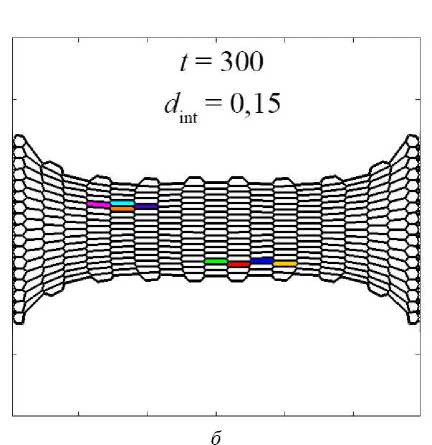
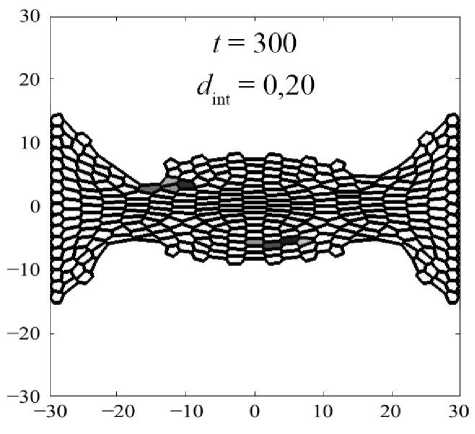
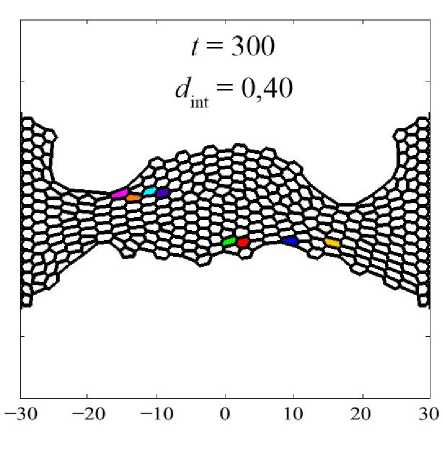
Видно, что при малых значениях параметра интеркаляции до d int = 0,15 включительно (рис. 5, а и б ) потенциальная энергия в ткани во время эволюции системы не отличается от случая к случаю. Это говорит о том, что при таких значениях d int не происходит интеркаляции клеток в ткани, о чём свидетельствует отсутствие графика на рис. 7 для случая d int = 0,15. Интеркаляция клеток наблюдается при d int = 0,20 (см. рис. 5, в и рис. 6) в последние моменты времени эволюции системы. Стоит отметить, что первые процессы интеркаляции клеток наблюдаются в областях с наибольшей потенциальной энергией в ткани (см. рис. 5, в ). А при значении d int = 0,25 наблюдается уже качественно другая картина в распределении потенциальной энергии? и форме ткани (см. рис. 5, г ) в конечный момент времени. При последующем увеличении параметра интеркаляции наблюдается уменьшение потенциальной энергии и стремление к равновесному состоянию происходит быстрее (см. рис. 5, д – е , и рис. 6). Также отметим, что при d int > 0,40 (см. рис. 6, б – г ) в ткани возникает эффект образования «узких» мест, дальше в тексте будем называть их «перемычками».

Эти перемычки связывают два участка ткани, первый – на который действует постоянная сила F 1 , второй – центральный, клетки которого практически не деформируются. Первый участок находится в постоянном

Параметры математической модели

μ	η	σ	φ	A 0	l 0	α 0
0,0	2,0	1,0	5,0	3√3 / 2	1,0	2π / 3

k	F 0	F 1	p 0	q	δ	β
0,5	0,1	0,1	5 ∙ 10–5	0,0	1,0	0,04

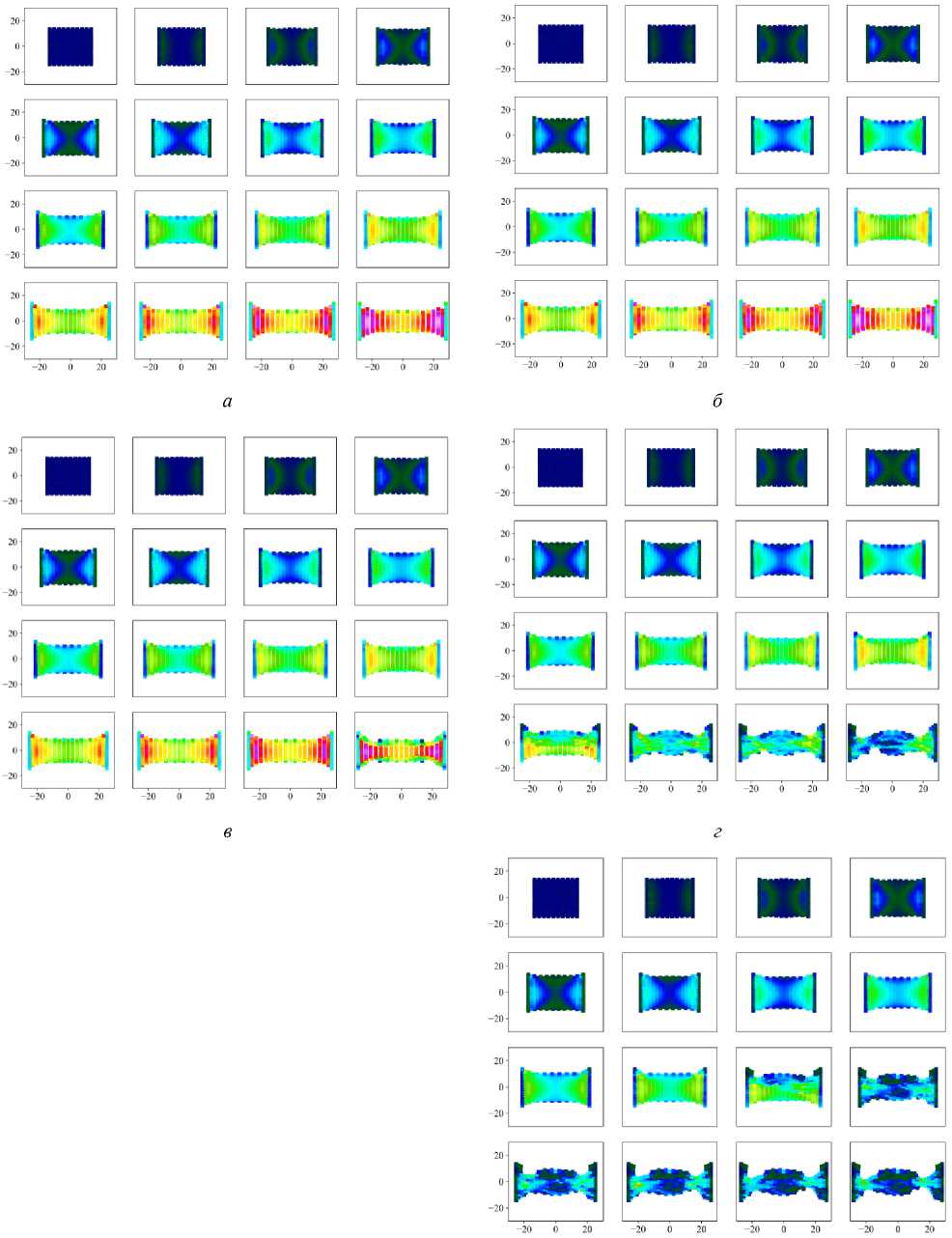
д                                                       е

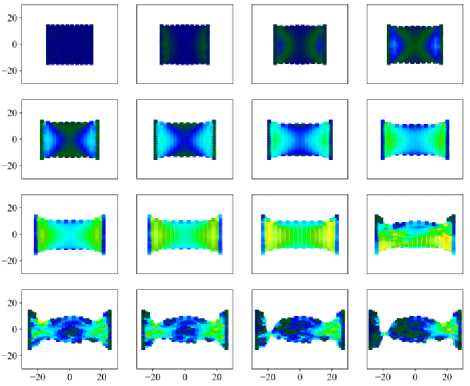
Рис. 5. Поле потенциальной энергии эпителиальной ткани при различных параметрах интеркаляции: а – d int = 0,00 и 0,05; б – d int = 0,10 и 0,15; в – d int = 0,20; г – d int = 0,25; д – d int = 0,30; е – d int = 0,35

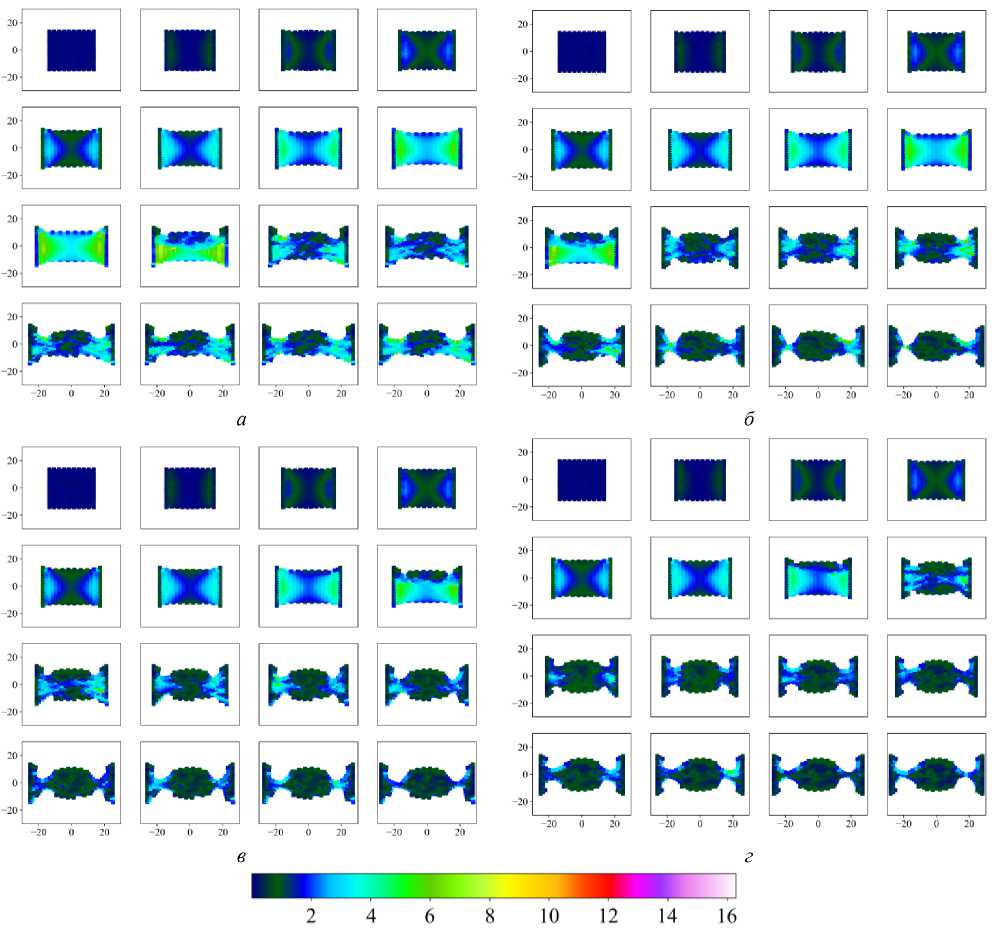
Рис. 6. Поле потенциальной энергии эпителиальной ткани при различных параметрах интеркаляции: а – d int = 0,40; б – d int = 0,45; в – d int = 0,50; г – d int = 0,55; 0,60; 0,65; 0,70

движении, а второй покоится и составляет большую часть недеформированной клеточной ткани. Вывод о недеформированных клетках в центральной части можно сделать на основе поля потенциальной энергии. Видно, что клетки в этой области имеют минимальные значения потенциальной энергии (см. рис. 6, б–г). Точно такие же значения потенциальной энергии наблюдаются в начальный момент времени. Так же, как и в случае с dint = 0,20 (см. рис. 5, в), при больших параметрах интеркаляции клетки начинают процессы переупаковки в областях с наибольшей потенциальной энергией – на рис. 6, б, начиная с 9-го кадра, на рис. 6, в, начиная с 8-го кадра, и на рис. 6, г начиная с 7-го кадра. Именно интеркаляционные процессы в этих областях способствуют формированию упомянутых выше перемычек. Их характерные масштабы по оси Y достигают 1–3 клеточных размеров, что меньше на 91–97 % от исходного размера ткани. Можно предположить, что скорее всего такие перемычки способствуют разрыву ткани, как говорится «где тонко, там и рвётся». С учётом всего вышесказанного сосредоточим внимание на подробном изучении ткани при параметрах dint от 0,15 до 0,40.

График на рис. 7 показывает общее количество интеркаляций клеток в каждом случае. Интересно отметить следующее. При d int = 0,30 в последние моменты времени происходит быстрое увеличение количества интеркаляций, т.е. в системе возникают достаточно высокие значения упругой энергии, клетки сильно деформируются (см. рис. 5, д ), что способствует интенсивной переупаковке клеток. Именно это обусловливает формирование узкой перемычки в данном случае. Также отметим, что процессы интеркаляции клеток возникают раньше при увеличении параметра интеркаляции d int . В работах [52–54] было показано, что относительное удлинение площади клеток, которое не приводит к её повреждению, составляет 30–40 %. Так мы можем

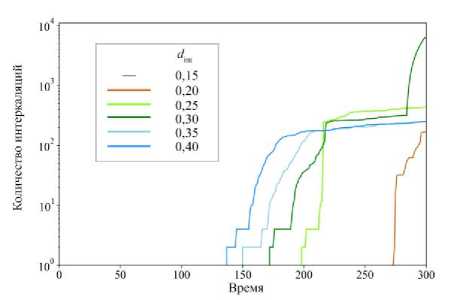
Рис. 7. Количество совершённых интеркаляций между клетками в ткани при различных параметрах интеркаляции d int . Время указано в расчётных единицах

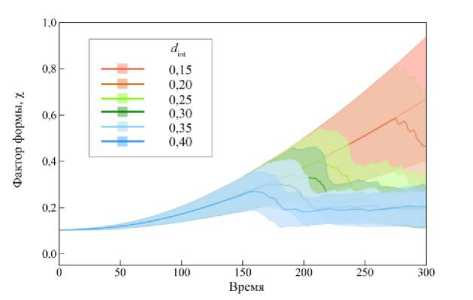
Рис. 9. Среднее значение фактора формы χ клеток ткани при различных параметрах интеркаляции d int (жирная линия). Закрашенной областью отмечено

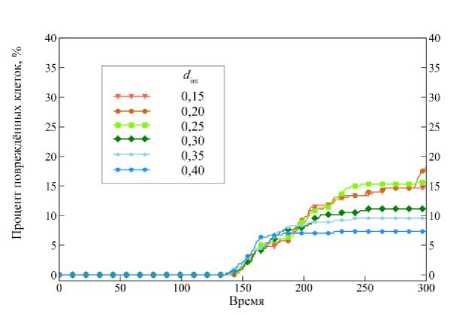
Рис. 8. Процент повреждённых клеток в ткани при различных параметрах интеркаляции d int . Время указано в расчётных единицах

оценить количество клеток, которое было повреждено в ходе одноосного растяжения при различных параметрах интеркаляции (рис. 8). За критическое значение площади было принято A крит = 7 / 5 ∙ A 0 . Мы считаем, что если площадь клетки больше, чем критическое значение ( A i >  A крит ), т.е. текущая площадь A i больше на 40 % равновесного значения A 0 , то она повреждена.

Из рис. 8 видно, что кривые при параметрах d int от 0,15 до 0,25 имеют примерно одинаковый процент повреждённых клеток, около 15 %. А при дальнейшем увеличении параметра интеркаляции процент повреждённых клеток уменьшается. Хорошо видно, как при d int = 0,40 наиболее интенсивно клетки изменяют свои размеры в интервале времени от 140 до 160 расчётных единиц, а в дальнейшем их число практически не изменяется. То есть можно сказать, что система устремилась к состоянию с минимальной потенциальной энергией.

Показательным параметром является фактор формы χ, определяемый следующим соотношением

X i =

P ² i

4πA

i

- 1

среднеквадратичное отклонение. Время указано в расчётных единицах

Если параметр χ → 0, это значит, что клетка имеет форму близкую, к окружности, и наоборот, если χ → 1, значит форма клетки сильно отклонена от формы окружности. Для правильного шестиугольника этот параметр имеет значение χ 0 ≈ 0,103. На рис. 9 представлен график изменения среднего значения параметра χ от параметра интеркаляции клеток d int . При параметре d int = 0,15 фактор формы χ в конце эволюции системы имеет максимальное отклонение от значения χ 0 , а при d int = 0,40 этот параметр вначале возрастает, а после момента времени t > 150 расчётных единиц устремляется к χ 0 . Это говорит о том, что при d int = 0,40 ткань развивается наиболее естественным образом, т.е. когда клетки ткани могут свободно перестраиваться, чтобы минимизировать испытываемую нагрузку и сохранить свою форму. Можно заключить, что моделирование наиболее естественного роста и развития эпителиальной ткани происходит при параметре d int = 0,40.

На рис. 10 показано, как произошла переупаковка двух клеточных ансамблей относительно их начального расположения в ткани (см. рис. 10 а ). Нижний ансамбль – клетки под номерами 43, 44, 52, 53, верхний ансамбль – клетки под номерами 221, 230, 231, 240. Данные ансамбли хорошо иллюстрируют два типа кластеров: которые образуют линии – нижний, которые образуют округлое скопление – верхний. Отчётливо видно, что при малых значениях параметра d int клетки не интерка-лируют друг с другом и остаются с таким же микроокружением, которое было в начальный момент времени (см. рис. 10, б ). При параметре d int = 0,20 хоть клетки и начинают перемещение в ткани посредством интеркаляции, отмеченные ансамбли не изменили своего положения друг относительно друга (см. рис. 10, в ), но их микроокружение изменилось. Из паттерна клеточной сетки на рис. 10, в , отчётливо видно, что клетки, расположенные вблизи горизонтальной оси симметрии ( Y = 0), очень сильно растянуты. Это говорит, что клетки в этой области не интеркалируют друг с другом,

в

г

Рис. 10. Переупаковка клеточных ансамблей при различных параметрах интеркаляции d int

а значит, эта область аккумулирует в себе избыточную потенциальную энергию. Значение параметра фактора формы χ у клеток в этой области стремится к максимальному отклонению от значения χ 0 . Наконец, при параметре d int = 0,40 (см. рис. 10, г ) отмеченные ансамбли сменили своё положение и микроокружение за счёт процессов интеркаляции. А паттерн клеточной сетки соответствует сетке с клетками одинаковых размеров [29].

Всё это свидетельствует, что клетки интенсивно меняют своё положение в ткани за счёт процесса интеркаляции. Что, в свою очередь, способствует эффективному устранению избыточных локальных напряжений во всей ткани. Данный процесс позволяет ткани развивать ся нормально и без возможных патологий, которые возникают из-за сильного растяжения клеток.

Также интересно обсудить траектории перемещения клеток (рис. 11). При параметре d int = 0,40 для нижнего ансамбля (клетки под номерами 43, 44, 52, 53),

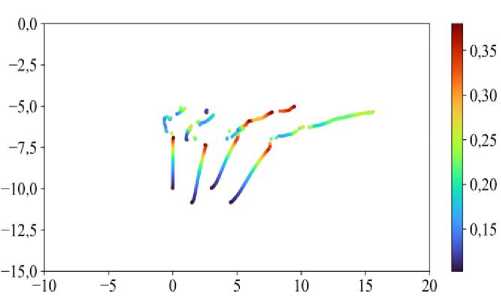
Рис. 11. Траектории перемещения центра масс клеток под номерами 43, 44, 52, 53 при параметре интеркаляции d int = 0,40. Цветом отмечено изменение индекса формы клетки χ в зависимости от её положения. Начальное положение клеток

соответствует минимальному значению χ 0

обсуждаемого на рис. 10, г . Из рис. 11 видно, что значение индекса формы клеток χ увеличивается до определённого момента времени. Это показывает, что клетки вытягиваются – увеличивается периметр. А начиная с некоторого времени t > 150 (см. рис. 9) значения параметра χ уменьшаются с последующими изменениями (рис. 11). При этом видно, что значение параметра χ при перемещении клеток в ткани стремится к минимальному значению у 3 клеток из 4. Такое скачкообразное изменение параметра χ говорит о том, что клетка совершила акт интеркаляции. Минимальное значение χ = χ 0 , а максимальное χ ≈ 0,38.

Таким образом, можно заключить, что при математическом моделировании развития эпителиальной ткани наиболее оптимальным параметром интеркаляции является d int = 0,40. Также можно предположить, что нормальная, не патологическая, эпителиальная ткань и её клетки ведут себя аналогичным образом как в наших численных экспериментах при d int = 0,40.

Заключение

В данной работе предложена и исследована математическая модель, описывающая процессы переупаковки клеток в эпителиальных тканях при механических воз-