Исследование процессов переупаковки клеток в эпителиальных листах in silico: часть II. Развитие ткани в условиях различных границ

RUSSIAN JOURNAL OF BIOMECHANICS

Компьютерные технологии позволяют исследовать биологические процессы in silico , исключая прямое вмешательство в живые ткани и организмы. Математическое моделирование позволяет прогнозировать эволюцию эпителиальной ткани, дополняя экспериментальные методы [1–7], и позволяет лучше понять биомеханику изменений в ткани при её развитии.

Переупаковка клеток – важный процесс, влияющий на морфогенез, регенерацию и адаптацию эпителиальных тканей к механическим воздействиям. Этот процесс становится особенно значимым при математическом моделировании развития тканей в различных условиях. Одним из ключевых направлений является изучение срастания клеточной массы, развивающейся в другой ткани. Здесь можно выделить работу [8], в которой рассматривается феноменологическая модель структурной перестройки костной ткани, основанная на критерии дифференциации клеток под воздействием внешнего механического стимула периодического характера. Для моделирования применяются уравнения колебаний сплошной среды, описываемой моделью пористого материала. Они решаются численно, с учётом жидкостного насыщения. Процесс образования клеток и их миграция в процессе сращения перелома принимаются случайными и ненаправленными, что описывается уравнением диффузии. Стоит отметить, что процесс срастания клеточной массы, развивающейся в другой ткани, связан с межтканевыми взаимодействиями, изменениями механических свойств границ между тканями и возможными особенностями миграции клеток в новую среду. Это значит, что при моделировании подобных процессов необходимо учитывать адгезионные свойства клеток, механические напряжения и динамику перестройки межклеточных контактов.

Другим важным аспектом является развитие эпителиальной ткани в условиях упругих и твёрдых границ. В этом случае поведение клеток определяется механическими свойствами окружающей среды, что приводит к различным сценариям деформации, упорядоченности клеточных структур и изменению характера переупаковки. Применение математических моделей позволяет изучить влияние жёсткости границ на распределение механического напряжения в ткани и предсказать возможные пути её морфогенетического развития. Примером может служить работа [9], в которой исследуется, как дифференциальные напряжения на клеточном уровне влияют на механическое поведение эпителиальных тканей. Авторы разрабатывают континуальную теорию для двумерной эпителиальной ткани, моделируемой с различными поверхностными натяжениями на апикальной, базальной и латеральных сторонах клеток. Исследование показывает, как клеточные свойства приводят к линейному, нелинейному и нелокальному эластическому поведению на уровне ткани. Особое внима- ние уделяется анализу потери устойчивости (баклинг) эпителия при сжатии, что имеет прямое отношение к пониманию влияния механических свойств окружающей среды на морфогенез эпителиальных тканей.

Развитие эпителиальной ткани также зависит от характера клеточного деления и интеркаляции. В условиях неравномерного деления клеток формируются различные паттерны роста, которые могут быть смоделированы с использованием дискретных методов, таких как клеточные автоматы, модель Поттса или вершинные модели [10]. В этом контексте важно учитывать параметры упругости клеточных мембран, межклеточных взаимодействий и влияние факторов, регулирующих пролиферацию. Стоит отметить, что работы по математическому моделированию неравномерного деления клеток эпителиальных тканей в ходе их развития встречаются крайне редко. Здесь мы можем выделить некоторые из наших работ [11; 12]. Как показано в нашей работе [13], интеркаляция клеток играет ключевую роль в ремоделировании ткани, обеспечивая её устойчивость и способность к адаптации под воздействием механических факторов.

Кроме того, моделирование процессов миграции клеток в ткани имеет особое значение для понимания механизмов заживления ран, морфогенеза и метастазирования опухолевых клеток. Использование численного моделирования позволяет проанализировать, как изменяются адгезивные свойства клеток, как организуется их движение и как формируются новые клеточные структуры. Например, в эпителиально-мезенхимальном переходе (ЭМП) математические модели помогают понять ключевые механизмы, определяющие подвижность клеток и их способность к инвазии.

Для математического моделирования описанных процессов применяются континуальные [14; 15] и дискретные подходы. Мы сосредоточили внимание на втором подходе. В дискретных методах математического моделирования, таких как вершинные модели, клетка представляется в виде многоугольника с динамически изменяющейся формой и размерами при взаимодействии с соседями. Этот подход особенно удобен для моделирования эпителиальных тканей, так как позволяет учитывать геометрию клеток, их межклеточные связи и механические свойства ткани [1; 16–20].

Недавние исследования показали, что вершинные модели позволяют качественно и количественно воспроизводить процессы клеточной переупаковки. В частности, в недавней работе [21] с их помощью было смоделировано интеркаляционное поведение клеток эпителиальной ткани в условиях механического растяжения, что позволило выявить ключевые параметры, определяющие организацию клеточной структуры. В другой работе [22] представлена модель epi-scale, комбинирующая элементы молекулярной динамики и вершинного подхода, что позволило учитывать взаимодействия на различных масштабах ткани. Сравнение с классическими вершинными моделями [23] показало, что усложнение модели не всегда оправданно, поскольку основные характеристики клеточной структуры могут быть успешно воспроизведены с использованием стандартных подходов.

Таким образом, мы продолжаем развивать предложенную ранее математическую модель [11; 12; 23; 24] для исследования механизмов клеточной переупаковки при различных условиях развития эпителиальной ткани. В данной работе рассматриваются процессы срастания разобщённых клеточных тканей, развитие ткани в условиях упругих и твёрдых границ, влияние неравномерного клеточного деления и интеркаляции, а также динамика клеточной миграции. Особое внимание уделяется анализу структурных изменений в ткани, роли механических и химических сигналов в её морфогенезе и устойчивости к внешним воздействиям. Разработанная модель учитывает процессы клеточного деления и интеркаляции, межклеточного взаимодействия, механической интеграции и биохимической регуляции.

Математическая модель

Подробно математическая модель описана в предыдущей работе [13]. Здесь мы изложим лишь её основные особенности.

Клетка в модели представлена в виде многоугольника. Существует три типа правильной мозаики плоскости: треугольная, квадратная и шестиугольная [9]. Оптимальной формой для моделирования клеток является правильный шестиугольник, поскольку он наиболее энергетически выгоден и приближен к окружности.

Для описания динамики системы используется уравнение потенциальной энергии:

N ( t )

U ( t ) = £N ( A ( t ) — A o ) + ^ P ² ( t ) +

= 1

+4: (l,(t) — lo )2 + ФХ (a,( t) — ao )2

J = 1                                  J = 1

Первое слагаемое отражает эластичность площади клетки с коэффициентом упругости n, A о — эталонное значение площади, а A i ( t ) вычисляется по формуле:

1     n ( t )

4⁽ tx ⁽ t ^{)+ x} j + 1 ⁽ t ) ) ■ ( J t ^)- y j + i ⁽ t ) ) ] ,    ⁽²⁾

² J = 1

где n - число вершин многоугольника, а x и y - координаты, образующие стороны клетки. Второе слагаемое в (1) описывает сократимость периметра клетки с коэффициентом ц, отражающим способность цитоскелета к сокращению. Третье слагаемое отвечает за эластичность рёбер клетки с коэффициентом G, где lij (t) - длина j -го ребра i-й клетки, а 10 - эталонная длина ребра шестиугольника. Четвёртое слагаемое характеризует эластичность углов с коэффициентом ф. aij(t) - текущее значение j-го угла i-й клетки в радианах, рассчитывается по формуле:

a.j ( t ) = arccos ( cos ( а._} ( t ) ) ) .                   (3)

Здесь cos(a j ( t )) определяется через скалярное произведение рёбер, образующих угол, а a₀ = 2п / 3 - эталонное значение угла. Для предотвращения появления многоугольников с отрицательными углами ф > 0. Суммирование в уравнении (1) для третьего и четвёртого слагаемых ведётся по числу рёбер клетки n ( t ), а общее суммирование ведётся по всем клеткам в системе N ( t ).

Эволюция ткани осуществляется за счёт перемещения вершин клеток. Вектор механической силы, действующей на вершину клетки, определяется как градиент потенциальной энергии:

F =-

J

д U ( t ) ^RT

Скорость перемещения клеток рассчитывается по механике Аристотеля, где сила определяет скорость движения:

V J = k F J H (I F j |- F o ) .                  (5)

Этот подход оправдан высокой вязкостью эпителиальной ткани, что подтверждается экспериментальными данными о низкой скорости перемещения иммунных клеток в эпителии.

Механизм клеточного деления вводится с вероятностью:

p div ( t ) = p o q" ⁽ t ^{)- 6},

где p ₀ и q - параметры, определяющие частоту деления. Если q > 1, деление более вероятно для клеток с n ( t ) > 6. Деление в модели реализовано следующим образом:

• 1.    определяется самое длинное ребро клетки;

• 2.    выбирается противоположное ребро;

• 3.    в их центрах создаются новые вершины;

• 4.    вершины соединяются новым ребром;

• 5.    обновляется список клеток.

Важный процесс в реальной ткани - интеркаляция. Этот процесс происходит при уменьшении длины ребра l ij ( t ) ниже критического значения d _mt, что приводит к повороту общей границы клеток на 90^о (рис. 1).

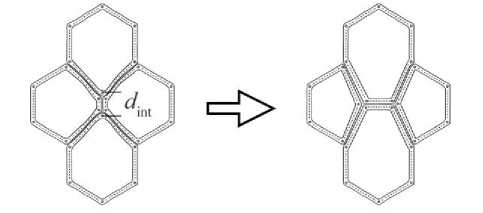
Рис. 1. Схематическое изображение процесса интеркаляции клеток в эпителиальной ткани

Кроме механических взаимодействий, модель учитывает химические процессы. Химические сигналы, такие как кислород или белки семейства RhoA , регулирующие цитоскелет, диффундируют между клетками согласно уравнениям:

Mt) = (Q(t)-c,(t))5lj (t),(7)

dC

' = SMt)-ec, (t),(8)

dt где δ – коэффициент диффузии, а Ci(t) – концентрация вещества, β – коэффициент деградации вещества. Хе-момеханическое взаимодействие описывается зависимостью механических параметров от концентрации химических сигналов:

n = n ( ^c i ( t ) ) ;   и = и ( ^c i ( t ) ) ;   ° = ° ( ^c i ( t ) ) ;

ф = ф (ci(t));   k = k (ci(t));   pо = pо (ci (t)).     ()

Предложенная математическая модель позволяет отслеживать динамику клеточной ткани, моделировать процессы деления, интеркаляции и межклеточного обмена сигналами. Эта модель относится к классу дискретных вершинных моделей и обеспечивает высокую точность описания клеточных процессов.

Результаты математического моделирования

Все результаты численного моделирования получены при одинаковых управляющих параметрах (таб. 1). Стоит отметить, что все величины указаны в произвольных единицах измерения, что позволяет легко перенастроить математическую модель под конкретный случай.

Установление контактов разобщённых тканей

Здесь мы исследуем скорость срастания двух отростков одной ткани, которая развивается в эпителии. В работе [13] нами было показано, что оптимальным параметром интеркаляции для переупаковки клеток развивающейся ткани является d int = 0,4. В этом случае

Таблица 1

Параметры математической модели

μ	η	σ	φ	A 0	l 0	α 0
0,0	2,0	1,0	5,0	3√3 / 2	1,0	2π / 3

k F0 p0 q dint δ С0 β 0,5 0,1 5 ∙ 10–6 1,4 0,4 1,0 10 0,04 мы имеем два типа развивающейся ткани: первая начинает рост из красной клетки в центре, и вторая, где происходит рост, жёлтые клетки (рис. 2, а). Здесь мы изучаем характеристики растущей ткани в зависимости от параметров интеркаляции для красной группы клеток. Для жёлтых клеток параметр интеркаляции принимает значение dint = 0,4, а для красных клеток этот параметр варьируется в диапазоне dred ϵ [0,1; 0,4] с шагом 0,1. Также дополнительно был проведён расчёт с dred = 0,05

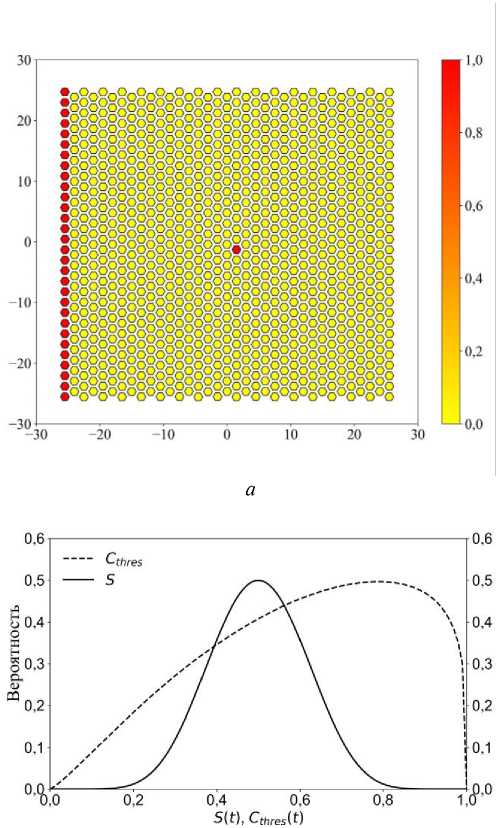
Начальные условия: в центре находится одна красная клетка, на левой границе – ансамбль красных клеток. Красные клетки, расположенные на левой границе, не испытывают процесс деления, а являются источником химического сигнала, который распространяется по ткани (рис. 2, б ).

Другие красные клетки, которые находятся в центре ткани, растут по градиенту этого химического сигнала. Функция вероятности для деления красных клеток записана в следующем виде:

pded (t ) = pdiv (t)+pc (t)+ps (t). (io)

Здесь p C ( t ) определяется выражением (11) и описывает вероятность деления клеток в зависимости от уровня химического сигнала C thres ( t ) в них. Значение функции C thres ( t ) определяется отношением (12), где C i ( t ) – значение концентрации химического сигнала в клетке, а C 0 – максимально возможное значение концентрации сигнала. Коэффициент k 1 – нормировочный коэффициент, равный k 1 = 3,0. График, показывающий распределение вероятности деления клеток (11), представлен на рис. 2, в , пунктирная линия.

(1 - Ch. (t))"    Clh2s (t)

11+(1 - c_ (t ))“i+cthis (>).

Сt

Ches (t ) = Y2.

C0

Третье слагаемое в уравнении (10) p S ( t ) определяется выражением (13) и показывает зависимость деления клетки от её микроокружения. Здесь мы полагаем, что красные клетки, которые находятся в контакте с жёлтыми, должны делиться интенсивнее, так как им поступает большее количество химического сигнала. Параметр S ( t ) определяется в зависимости от микроокружения по формуле (14), где n r ( t ) – количество красных клеток вокруг текущей. Из формулы (14) видно, что значение индекса S изменяется от 0 до 1. Значение «0» соответствует случаю, когда красная клетка полностью окружена красными клетками, а «1» соответствует случаю, когда красная клетка окружена жёлтыми. Все промежуточные значения соответствуют различному микроокружению клетки. Иначе говоря, значение этого индекса S ( t ) показывает положение красной клетки относительно других красных клеток. Коэффициент k 2 в

в                                                                  г

Рис. 2. а – Поле функции состояния клеток в момент времени t = 0; б – поле концентрации постоянного химического сигнала; в – график распределения вероятностей деления клеток для уравнений (11) – пунктирная линия и (13) – сплошная линия; г – график распределения вероятности деления клеток для уравнения (6)

уравнении (13) является нормировочным и принимает значение k 2 = 33000. График распределения функции (13) показан на рис. 2, в , сплошная линия.

Ps ( t ) = ^k 2

( 1 - s ( t ) ) 8      s ( t ) 8

1 + ( 1 - S ( t ) ) 8 1 + s ( t ) 8 .

^s ( t ) =

n ( t ) - n r ( t ) n ⁽ t )

На рис. 2, г , представлено распределение вероятности деления для выражения (6). Уравнение (10) является суммой трёх вероятностей (6), (11) и (13).

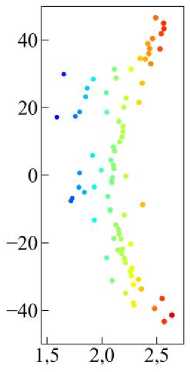
График смещения центра масс (рис. 3) растущей ткани наглядно показывает, по какой траектории происходит движение развивающейся клеточной массы из красных клеток. Клетки в модели представлены в виде многоугольников. Тогда центр масс ткани из красных клеток можно рассчитать стандартным методом разбиения:

r ( ^t )                                      N r ( t )

x, A(t)xi(t)          E, AAt)y>(t)

i = 1                                         = 1

A total ( t )      ’ cm =       A total ( t )

Здесь A i ( t ) – площадь i -й клетки, x i ( t ) и y i ( t ) – координаты центра i -й клетки, A total ( t ) – сумма площадей всех красных клеток, N r ( t ) – число красных клеток в системе. Таким образом для каждого момента времени мы можем рассчитать положение центра масс ткани X cm и Y cm , состоящей из красных клеток.

Из рис. 3 отчётливо видно, что при низком значении параметра интеркаляции dred = 0,05 наблюдается максимальное смещение центра масс в направлении источника химического сигнала. Этот эффект обусловлен тем, что при столь низкой подвижности красные клетки оказываются механически «жёсткими», и вся нагрузка перераспределяется на жёлтую ткань. Поскольку жёлтые клетки имеют высокую интеркаляционную подвижность dint = 0,4, они начинают активно перестраи- ваться под действием избыточного давления, создавая благоприятные условия для продвижения красной ткани к источнику химического сигнала.

По мере увеличения параметра d ^red от 0,1 до 0,3 наблюдается поступательное снижение скорости смещения центра масс. Это можно объяснить тем, что с ростом интеркаляционной способности красных клеток часть механического напряжения начинает компенсироваться внутри самой красной ткани, тем самым сни жается передача давления на жёлтую ткань, и прорастание замедляется

Наибольшее снижение динамики прорастания фиксируется при d ^red = 0,5 (см. рис. 3), что также подтверждается графиком изменения энергии на одну клетку U 1 на рис. 4. Здесь кривая для d ^red = 0,5 демонстрирует заметно более низкие значения U 1 по сравнению с остальными случаями. Это указывает на то, что при высокой интеркаляционной подвижности клетки эффективно перераспределяют внутренние напряжения, снижая накопление потенциальной энергии в системе. Однако такая энергетическая гибкость одновременно приводит к тому, что красная развивающаяся ткань теряет направленность движения – силы, приводящие к перестройке ткани в сторону химического градиента, рассеиваются внутри неё.

Интересно отметить, что на графике энергии (рис. 4) кривые для d ^red располагаются очень близко друг к другу, кроме d ^red = 0,5. Это говорит о наличии некоторого плато – диапазона значений интеркаляции, в котором изменения энергии системы минимальны, несмотря на выраженные различия в кинематике прорастания (см. рис. 3). Такое поведение можно интерпретировать как переходную зону между режимами «выталкивания» красной ткани жёлтой и самодвижения красных клеток.

Таким образом, можно заключить, что максимальное прорастание обеспечивается при низких значениях интеркаляции красной ткани, когда основную роль в перестройке играет жёлтая ткань. При высоких значениях интеркаляции происходит перераспределение напряжений внутри красной ткани, что снижает как среднюю энергию системы, так и степень направленного движения.

Случай d ^red = 0,4 особенно интересен, потому что он представляет собой своего рода оптимальный баланс между подвижностью клеток и способностью ткани к целенаправленному прорастанию. Рассмотрим его подробнее. На рис. 3 (зелёная линия) видно, что смещение центра масс находится примерно посередине между случаями с низкой d ^red = 0,05 и высокой подвижностью d ^red = 0,5. То есть прорастание красной ткани не такое интенсивное, как при низкой подвижности, но и не тормозится, как в случае, когда красная ткань «размягчается» и теряет направленность движения ( d ^red = 0,5). Это говорит о том, что при d ^red = 0,4 клетки обладают достаточной гибкостью для адаптации к механическим

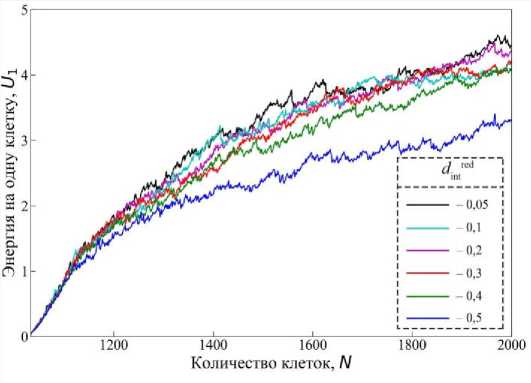
Рис. 4. График энергии на одну клетку U 1

при различных параметрах интеркаляции для красных клеток. Энергия на одну клетку U1 указана в произвольных единицах

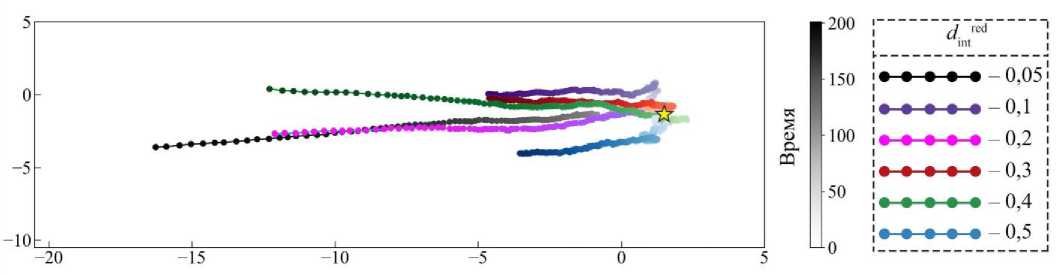
Рис. 3. График смещения центра масс развивающейся ткани из красных клеток при различных параметрах интеркаляции d ^red . Жёлтым символом отмечено начальное положение первой красной клетки. Градиентным

изменением цвета от белого к насыщенному представлено время эволюции системы. Представленные траектории являются осреднёнными для 10 расчётов в каждом случае. Время указано в произвольных единицах нагрузкам, но при этом сохраняют способность к коллективному смещению по градиенту химического сигнала. Из рис. 4 видно, что в этом случае значения энергии на одну клетку Ui находятся ниже, чем в случаях с меньшей интеркаляцией (чёрная, розовая, бирюзовая, красная линии), но выше, чем при d^ = 0,5 (синяя линия). То есть система испытывает умеренное напряжение: не такое высокое, как при низкой интеркаляции, но и не столь низкое, как при высокой. Это подтверждает наличие эффективной механической адаптации ткани без потери направленности движения. Такой параметр интеркаляции представляет собой компромиссное значение, при котором красная ткань сохраняет высокую подвижность, позволяющую эффективно перераспределять внутренние напряжения. Одновременно с этим ткань не теряет координации и может прорастать в сторону источника химического сигнала. Можно сказать, что это режим синергии подвижности и направленности роста, когда ткани взаимодействуют не конфликтно, а согласованно. Следовательно, ключевым фактором в описываемой динамике является не столько изменение энергетического ландшафта, сколько уровень локальной подвижности клеток на границе двух тканей.

Рост ткани в условиях упругих и твёрдых внешних границ

В этом разделе приводятся результаты моделирования роста эпителиальной ткани в условиях упругих и твёрдых внешних границ. Были рассмотрены случаи наличия в системе всех четырёх твёрдых границ с постепенным добавлением по одной упругой границе. Начальные условия: ткань состоит из 1033 правильных гексагональных клеток, клетки делятся согласно

распределению вероятности (6), внешние границы определены квадратной областью X е [-27; 27], Y е [-27; 27] (рис. 5).

Для случая твёрдых границ наблюдается картина постепенного роста упругой потенциальной энергии в системе (см. рис. 6). В такой геометрии интересно оценить возникающие в системе максимальные касательные напряжения. Большой интерес эта информация представляет в области тканевой инженерии в направлении разработки скаффолдов. В данном случае мы не рассматриваем рост эпителиальной ткани в скаффолдах, а её развитие в ограниченном пространстве, что по сути является частным случаем упомянутого направления.

Для того чтобы оценить максимальные касательные напряжения в упругопластической системе, необходимо вычислить собственные значения Х₁ и Х₂ тензора напряжений Коши для каждой клетки. Тензор напряжений g i для каждой i -й клетки рассчитывается по данным координат вершин клетки R ij = ( x ij , y ij ) и силам F y = ( F ijx , F ij ), действующим на эти вершины, по следующей формуле:

1 n ( t )

°'= — 2^ 5 R — R i l’ Fl’ ⁽¹⁶⁾

Здесь A i ( t ) - это площадь клетки, R ij - координаты вершины клетки, R i - координаты центра клетки, суммирование ведётся по всем вершинам клетки-многоугольника. Поскольку у нас двумерная задача, то тензор g i будет иметь вид матрицы 2*2:

ст     ст xx      xy

ст     ст yx       yy

Рис. 5. Начальные условия системы

где g xx и g yy - нормальные напряжения вдоль осей x и у , а g xy и g yx - касательные напряжения. Собственные значения Х₁ и Х₂ можно найти, решив характеристическое уравнение вида:

det (ст, -XI) = 0,

где I - единичная матрица. Подставив (17) в характеристическое уравнение (18) и раскрыв определитель, получим квадратное уравнение:

X2-(ст +ст )Х + (ст ст -ст ст ) = 0,     (19)

xx       yy             xx yy       xy yx         ,

корни которого:

Xu

ст +ст xx       yy

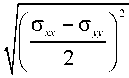
+ ст ст xy yx

,

и будут собственными значениями Х₁ и Х₂ тензора напряжений g i . Добавим пару слов о интерпретации собственных значений. Если Х₁, Х₂ > 0, то будут наблюдаться растяжения в клетке по двум осям, если Х₁, Х₂< 0, то в этом случае будет наблюдаться сжатие по двум осям, а если Х₁ и Х₂ имеют разные знаки, то в этом случае будут наблюдаться сдвиговые деформации.

Тогда максимальные касательные напряжения в клетках ткани можно определить следующим образом:

.   = ^1 -^2

max

На рис. 7 представлена карта максимальных касательных напряжений τ max для конечного момента времени t = 500 в случае развития эпителиальной ткани в условиях твёрдых границ с областью X и Y ϵ [–27; 27]. Отчётливо видно, как распределена интенсивность сдвиговых деформаций в ткани – повышенные значения локализованы вдоль верхней и нижней границ. В центральной части клетки находятся в механическом равновесии, и значительных внутренних сдвигов не наблюдается. Эпителиальные ткани, особенно в моделях роста на фиксированной подложке или между жесткими стенками, показывают характерную картину распределения напряжений: в центре – покой, на краях – напряжённые зоны.

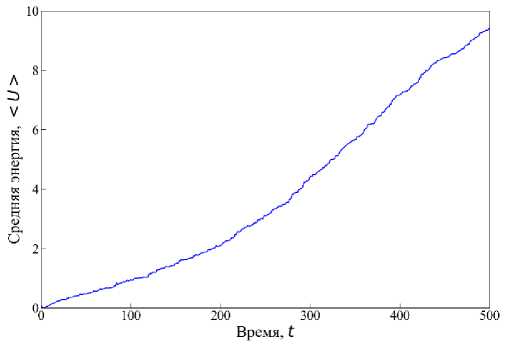
Рис. 6. Изменение средней энергии < U > ткани, развивающейся в условиях твёрдых границ. Время и средняя энергия указаны в произвольных единицах

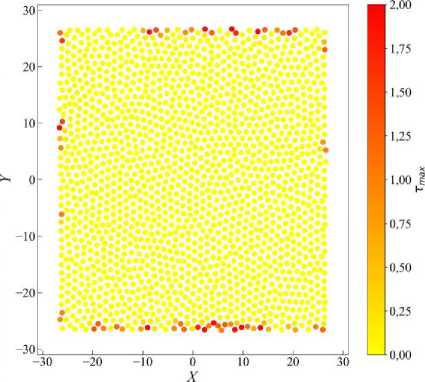
Рис. 7. Карта максимальных касательных напряжений в клетках эпителиальной ткани, развивающейся в условиях твёрдых границ. Карта представлена для конечного момента времени эволюции системы t = 500

Такие зоны могут быть потенциальным местом, где активируются механочувствительные сигнальные пути (например, активация кадгеринов или интегринов, связанных с восприятием напряжений) [25].

В реальных биологических системах локальные повышения τ max могут инициировать процессы ремоделирования ткани, апоптоза или активной миграции клеток к краю. В жёстко ограниченных тканях краевые зоны испытывают максимальное напряжение, что может запускать апоптоз. Центральные области, оставаясь менее напряжёнными, могут избегать гибели клеток [26].

Проведём сравнение результатов со случаем комбинированных граничных условий: твёрдые границы слева и снизу, упругие – справа и сверху. Упругие границы были заданы с помощью закона линейной упругости:

F border =± z ( x - x ^border ) ,

border                       border

где z – коэффициент упругости, X ^border, Y ^border – координаты границы, а X и Y – координаты узлов клетки. Таким образом, появляется сила со стороны границ, направленная по нормали в толщу ткани. Был исследован рост ткани в зависимости от коэффициента упругости границ z . Коэффициент принимал значения из интервала z ϵ [0,5; 1,0] с шагом 0,05. Рассмотрим распределение касательных напряжений T max в эпителиальной ткани при различных коэффициентах упругости z .

На рис. 8 представлены карты распределения максимальных касательных напряжений T_max в эпителиальном монослое в конечный момент времени t = 500 для двух случаев с различным коэффициентом упругости верхней и правой границ: z = 0,5 (рис. 8, а ) и z = 1,0 (рис. 8, б ). Каждая точка на карте соответствует отдельной клетке, а цвет отражает значение T_max, характеризующее локальные сдвиговые деформации.

При относительно мягких упругих границах z = 0,5 (см. рис. 8, а ) наблюдается более равномерное распределение напряжений по ткани. Зоны повышенных значений T_max (оттенки оранжевого и красного) располагаются не только вдоль твёрдых границ, но и в периферийных областях, включая верхнюю часть ткани. Это указывает на активную переработку механических сигналов клетками в ответ на локальные деформации и рост, согласующуюся с известной механосенситивностью эпителиальных клеток [27]. Гибкость границ способствует частичной релаксации напряжений и увеличивает вариативность локальных механических состояний. С увеличением жёсткости упругих границ z = 1,0 (см. рис. 8, б ) картина заметно изменяется. Максимальные значения T_max концентрируются преимущественно вдоль нижней твёрдой границы и верхней упругой. В это же время центральная часть ткани становится более механически напряжённой Об этом можно судить по наличию кластера клеток с T_max > 0 в центральной области ткани.

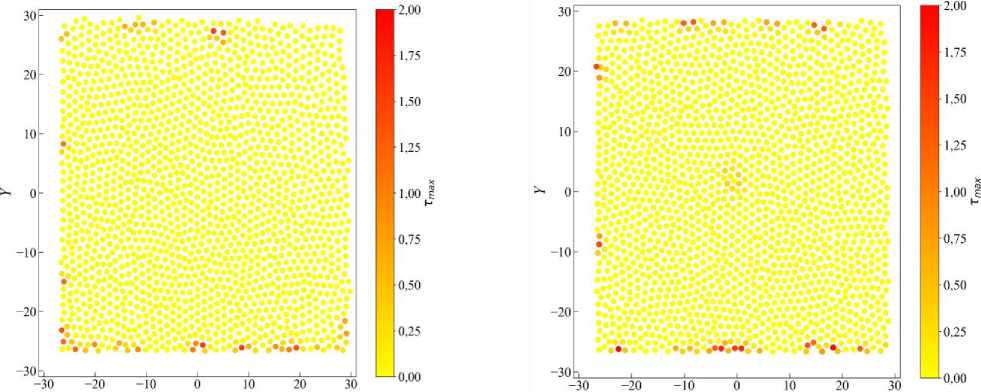
A'

а                                                    б

Рис. 8. Карты максимальных касательных напряжений в клетках эпителиальной ткани в случае комбинированных граничных условий: твёрдые границы слева и снизу, упругие – справа и сверху. Карты представлены для конечного момента времени эволюции системы t = 500. Коэффициент упругости для границ: а – z = 0,5; б – z = 1,0

Количество клеток с высоким значением максимальных касательных напряжений T max увеличилось. Это указывает на ограничение перераспределения механической энергии через жёсткие границы, что способствует локализации сдвиговой деформации на периферии [28] и в центральной области. Наблюдаемые различия обусловлены характером механического взаимодействия клеток с окружающей средой. При меньшей жёсткости границ эпителий способен компенсировать внутреннее давление и локальные деформации посредством смещений упругих стенок.

Однако при более жёстких границах происходит аккумуляция напряжений вблизи фиксированных краёв, что создаёт локальные механически активные зоны и усиливает сдвиговую нагрузку на клетки у периферии. Это может оказывать влияние на процессы коллективной миграции, апоптоза, пролиферации и морфогенеза [29; 30]. Полученные результаты согласуются с экспериментальными наблюдениями касательных напряжений в эпителии in vitro. Сравнивая развитие ткани в условиях комбинированных границ и абсолютно твёрдых, можно заключить следующее. В случае абсолютно твёрдых границ наблюдается выраженное накопление касательных напряжений вдоль периметра ткани (см. рис. 7), особенно в верхней и нижней частях. Пространственное распределение напряжений характеризуется высокой симметрией и резкими градиентами на границах, что указывает на ограниченные возможности перераспределения механической энергии клетками эпителия. Локальные максимумы Tmax достигают предельных значений, занимая относительно широкие зоны вдоль границ. При переходе к условиям упругих границ (см. рис. 8) наблюдается снижение интенсивности и локализации касательных напряжений у упругих сторон (вверху и справа). При z = 0,5 (см. рис. 8, а) напряжения су- щественно сосредоточены вблизи твёрдых границ (внизу и слева), тогда как в случае z = 1,0 (см. рис. 8, б) происходит частичное перераспределение напряжений, и зона их повышенной концентрации расширяется. Таким образом, с увеличением жёсткости упругих границ система демонстрирует рост симметрии в распределении fmax, однако общая степень локализации остаётся ниже, чем при полностью твёрдых границах. Биофизически такие различия объясняются тем, что при наличии упругих границ клетки имеют возможность деформировать внешнюю среду, снижая внутренние напряжения и препятствуя их накоплению в пограничных областях. В условиях жёстких ограничений, наоборот, ткань вынуждена накапливать касательные напряжения вблизи периферии, что может приводить к повышенному риску механически индуцированных событий – таких как морфогенетические перестройки, пролиферация или апоптоз клеток [31; 32].

Развитие ткани в условиях неравномерного деления клеток и их интеркаляции

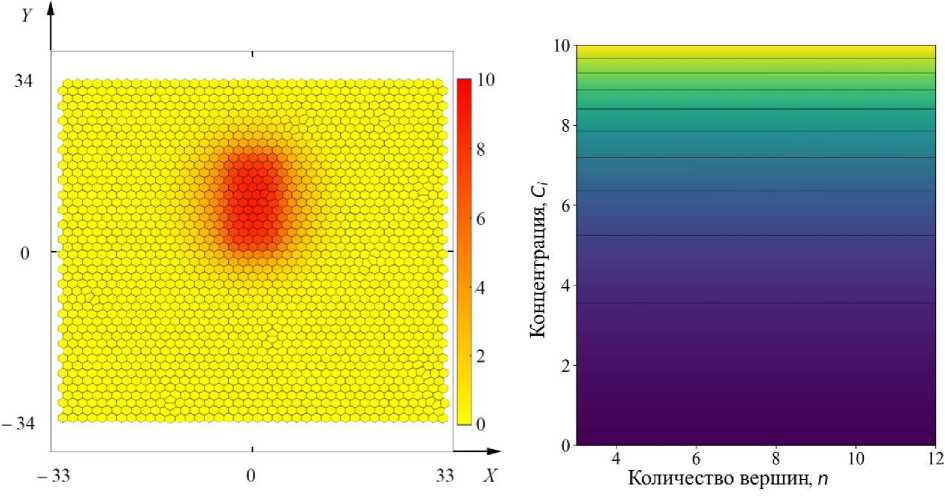
Было исследовано влияние неравномерного процесса деления и интеркаляции на структуру ткани в ходе её развития. Т.к. в математической модели деление клеток происходит вероятностным образом, то под равномерным делением понимается равновероятное деление для каждой клетки. Неравномерный (неравновероятный) процесс деления был реализован следующим образом. В прямоугольной области ткани X ϵ [–5; 5], Y ϵ [0; 20] был задан источник химического сигнала:

dC = ( C 0 - C i ) u ( t ) ,

где u ( t ) – функция, управляющая скоростью выравнивания концентрации к предельному значению C 0 .

0,1356

0,1227

0,1098

0,0969

0.0841 £ о

0,0712 | о

0.0454

0.0325

0,0196

0,0067

б

а

Рис. 9. а - Поле концентрации химического сигнала (24) в клетках в начальный момент времени t = 0 эволюции системы; б - карта значений вероятности деления клеток (25)

Функция выравнивания концентрации задана линейной зависимостью от времени u ( t ) = 0,1 1 . Вероятность деления (6) клеток, в которых происходит превышение концентрации химического сигнала C i ( t ) > 2,5, была записана в следующем виде:

n ( t ) - 6 , 0.3 C ( t ) - 5

p div ( t ) = p о q + e , (25)

т.е. клетки в области X е [-5; 5], Y е [0; 20] и прилегающие к ним с концентрацией больше 2,5 единицы делятся вероятнее, чем остальные клетки. Состояние клеточной ткани в начальный момент времени t = 0 и карта значений вероятности деления клеток (25) представлены на рис. 9. Был рассмотрен случай активации и ингибирования деления клеток химическим сигналом. В случае ингибирования в уравнении (25) экспоненциальное слагаемое вычитается. Рассмотрим и сравним эти случаи друг с другом. На рис. 10 представлены границы ткани в начальный момент времени (серый контур), а также в случае активации (красный контур) и ингибирования (синий контур) в конечный момент времени t = 300 эволюции системы. Наблюдается значительное различие в геометрии ткани между двумя режимами. В случае активации деления клеток (анизотропное деление с высоким уровнем пролиферации) ткань демонстрирует выраженное расширение за пределы изначального прямоугольного контура, принимая округлую, радиально симметричную форму. Это указывает на усиленный радиальный рост, обусловленный как пролиферацией, так и ориентацией митозов в направлении, благоприятствующем расширению. В противоположность этому, при ингибировании деления ткань сохраняет общую форму прямоугольного контура.

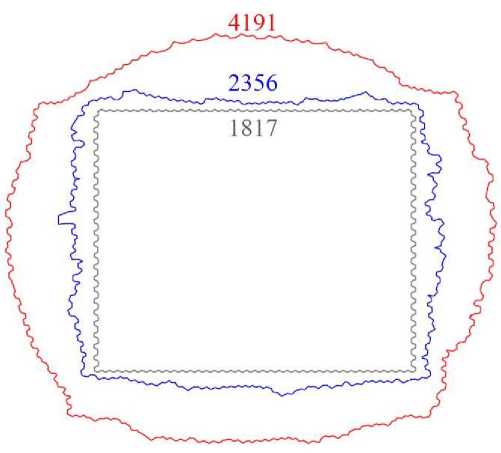
Рис. 10. Границы ткани в начальный момент времени t = 0 (серая линия) и в конечный момент времени t = 300 (красная и синяя линии). Красная граница соответствует случаю активации деления клеток, синяя граница -ингибированию деления. Цифрами указано количество клеток в системе для каждого из этих сценариев

В то же время она демонстрирует меньшую степень тканевого расширения и выраженную пространственную анизотропию в распределении размеров клеток.

На рис. 11 представлены срезы распределения размеров клеток вдоль центральной вертикальной оси X е [-1; 1] в ткани для случаев активации (рис. 11, а ) и ингибирования (рис. 11, б ) деления.

В активированном режиме (см. рис. 11, а ) наблюдается увеличение среднего размера клеток от центра к периферии, что связано с усиленным делением в центральной зоне и меньшей плотностью клеток на периферии вследствие расширения.

При ингибированном делении (см. рис. 11, б ) сохраняется более равномерное распределение размеров клеток вдоль оси, однако заметна градиентная структура, указывающая на влияние механических ограничений на клеточный рост. Можно заключить, что активное деление клеток и его направленность оказывают существенное влияние на форму, размер и механическую гетерогенность эпителиальной ткани. Анизотропное деление способствует экспансивному росту и усилению тканевого давления, тогда как ингибирование приводит к уплотнению и замедлению морфогенеза.

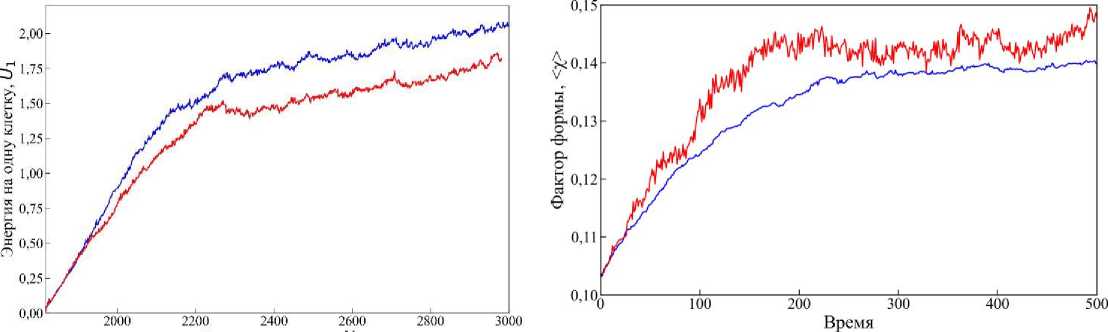
Интересным параметром в этом случае является энергия, приходящаяся на одну клетку U1. Из рис. 12 видно, как изменяется U1 в каждом случае. В случае ингибировании энергия U1 растёт монотонно (синяя линия), а в случае активации наблюдается рост быстрыми темпами (красная линия). При достижении одинакового числа клеток в каждом сценарии значение U1 для случая активации больше примерно в 4 раза, чем в случае ингибирования. Как указано на рис. 10, в конечный момент времени t = 300 для случая ингибирования деления клеток в системе наблюдается N = 2356 клеток, а для случая активации – N = 4191. На врезке рис. 12 представлен график изменения U1 для случая активации до конечного момента времени t = 300. Видно, что рост энергии в такой системе прекращается после достижения определённого числа клеток, и даже немного уменьшается при дальнейшей эволюции ткани и выходит на постоянное значение. Это говорит о том, что клеточная ткань приходит в равновесное состояние, несмотря на продолжающееся деление клеток. Такой выход на стационарный уровень удельной энергии свидетельствует о наличии эффективного механизма перераспределения механических напряжений в ткани, который компенсирует локальные деформации, возникающие в результате пролиферации [33]. Кроме того, достижение плато в кривой U1 может быть связано с геометрическим насыщением плотности клеток и ограниченной возможностью дальнейшего уплотнения ткани без существенной перестройки клеточной топологии [16; 23].

В противоположность этому, в случае ингибирования деления клеток энергия на клетку растёт медленно, но устойчиво на протяжении всей эволюции системы. Отсутствие активного прироста клеточной популяции не приводит к механической перегрузке системы, однако не даёт ей также перераспределить напряжения через обновление клеточной конфигурации. В этом случае ткань медленно накапливает механическую энергию из-за роста клеток и ограниченных возможностей их перемещения в плотной среде [28].

Таким образом, сравнение сценариев активации и ингибирования деления демонстрирует два различных механизма самоорганизации эпителиальной ткани. В условиях активации деления система использует клеточную пролиферацию для перераспределения энергии и выхода на стабильное состояние. В условиях ингибирования отсутствует такой канал релаксации, и ткань постепенно накапливает механическое напряжение, что может иметь последствия для её морфогенеза, устойчивости и отклика на внешние воздействия.

Рассмотрим неравномерный процесс интеркаляции клеток в развивающейся ткани. Неравномерный процесс интеркаляции был реализован аналогичным образом, как это было сделано в случае неравномерного

а

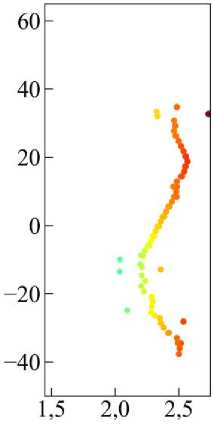
Рис. 11. Срезы распределения размеров клеток вдоль центральной вертикальной оси X ϵ [–1; 1] в ткани для случаев: а – активации деления клеток; б – ингибирования деления клеток

процесса деления клеток. В той же прямоугольной области ткани X ϵ [–5; 5], Y ϵ [0; 20] был задан источник химического сигнала уравнением (24), который определяет параметр интеркаляции dint. В случае активации процесса интеркаляции этот параметр принимал значение dint = 0,5, а в случае ингибирования – dint = 0,1, т.е. при активации процесса интеркаляции клетки, в которых уровень химического сигнала Ci > 2,5, более склонны к перезамыканию, чем клетки, в которых отсутствует этот сигнал. И наоборот в случае ингибирования.

Состояние клеточной ткани в момент времени t = 0 соответствует тому, что представлено на рис. 9, а . В каждом случае деление клеток было реализовано согласно распределению (6). Рассмотрим каждый из них подробнее. Из рис. 13 видно, что размеры ткани для каждого случая в конечный момент времени имеют одинаковые размеры. Аналогичный вывод можно сделать из распределения размеров клеток вдоль центральной вертикальной оси X ϵ [–1; 1] в ткани (рис. 14). Из представленных графиков на рис. 14 видно, что клетки имеют одинаковые размеры. В центральной части ткани наблюдается скопление клеток малых размеров, а ближе к периферии – более крупные клетки. В целом, картина выглядит так, как будто ткань в каждом случае развивается одинаково. Но вот график изменения энергии на одну клетку U 1 (рис. 15) демонстрирует другую картину. Видно, что в случае активации интеркаляции клеток значение U 1 оказывается меньше (рис. 15, красная линия), чем в случае ингибирования интеркаляции (рис. 15, синяя линия). Это говорит о том, что в случае активации интеркаляции ткань способна эффективнее перераспределять механическое напряжение за счёт изменений топологии клеточного слоя.

В отличие от этого, при ингибировании интеркаляции ткань ограничена в возможности топологических

Среднее значение параметра <χ> рассчитывается

как	N ( t ) E x ,
	~ N ( t ) ,	(26)
где	x =      - 1. '    4 n A.	(27)

Фактор формы χ i (27) отражает степень округлости клетки, при этом значения ближе к нулю соответствуют более круглым клеткам, а большие значения указывают на вытянутые или деформированные формы клеток.

На графике для случая ингибирования интеркаляции (синяя линия на рис. 16) наблюдается плавный, монотонный рост среднего значения фактора формы от начального значения χ 0 ≈ 0,103, соответствующего для правильного шестиугольника, до значения <χ> ≈ 0,14 к конечному моменту времени t = 500. При этом характер кривой относительно сглажен, без выраженных скачков и флуктуаций.

Это может свидетельствовать о стабильной, медленной перестройке клеточной структуры без существенных локальных перестроек формы клеток. В отличие от этого, график для случая активации интеркаляции (красная линия на рис. 16) демонстрирует более динамичное поведение. Среднее значение фактора формы также растёт со временем, достигая значений <χ> ≈ 0,15, однако процесс сопровождается ростом напряжений, особенно в центральной части, где наблюдается наибольшая плотность клеток. Это сказывается на более высоком среднем значении U 1 и может приводить к менее стабильному состоянию ткани на поздних этапах её развития.

перестроек, что приводит к накоплению локальных

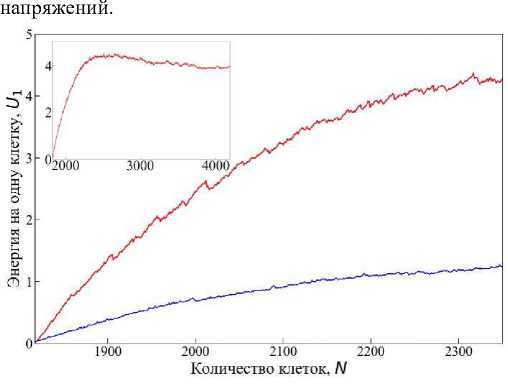
Рис. 12. Энергия на одну клетку U 1 для случая активации (красная линия) и ингибирования (синяя линия) деления клеток. На врезке представлен график энергии на одну клетку U 1 для случая активации до конечного момента времени t = 300. Энергия на одну клетку U 1 указана в произвольных единицах

Рис. 13. Границы ткани в начальный момент времени t = 0 (серая линия) и в конечный момент времени t = 500 (красная и синяя линии). Красная граница соответствует случаю активации интеркаляции клеток, синяя граница – ингибированию интеркаляции. Цифрами указано количество клеток в системе для каждого из этих сценариев

а

б

Рис. 14. Срезы распределения размеров клеток вдоль центральной вертикальной оси X е [-1; 1] в ткани для случаев: а - активации интеркаляции клеток; б - ингибирования интеркаляции клеток

Количество клеток. N                                                                            .

Рис. 16. Среднее значение фактора формы <х> клеток

Рис. 15. Энергия на одну клетку U 1 для случая           эпителиальной ткани для случая активации (красная

активации (красная линия) и ингибировании (синяя линия) интеркаляции клеток. Энергия на одну клетку U1

линия) и ингибировании (синяя линия) интеркаляции клеток. Время указано в произвольных единицах указана в произвольных единицах

Показательным параметром для сравнения этих двух случаев является среднее значение фактора формы клеток <х>. На рис. 16 приведены графики изменения среднего значения фактора формы клеток <х> от вре-мевыраженными флуктуациями. Видны участки резких изменений плато и нестабильностей. Это указывает на более активную морфогенетическую перестройку ткани.

С биофизической точки зрения различия между графиками объясняются спецификой действия интеркаляции клеток. Интеркаляция - это процесс, при котором клетки перемещаются относительно друг друга, что приводит к изменению связей с соседними клетками и способствует перераспределению механических напряжений в ткани. В случае активации интеркаляции клетки чаще изменяют своё микрокоружение, что способствует перераспределению формы клеток и, как следствие, приводит к менее регулярной, но более активно адаптирующейся структуре.

Это отражается в более высоком среднем значении фактора формы и его нестабильной динамике. Напротив, при ингибировании интеркаляции клеточные связи остаются более постоянными, ткань развивается более упорядоченно, и процесс деформации клеток идёт равномерно и медленно.

Несмотря на схожие макроскопические размеры ткани и распределение размеров клеток, внутреннее механическое состояние системы оказывается существенно различным. Этот результат подчёркивает важность клеточной интеркаляции как механизма релаксации, обеспечивающего снижение внутренней энергии и, как следствие, более устойчивое морфогенетическое поведение ткани. Таким образом, результаты моделирования демонстрируют, что активация интеркаляции способствует более интенсивному морфогенетическому ремоделированию ткани, сопровождающемуся временными и пространственными флуктуациями формы клеток. Это может быть важным биофизическим механизмом адаптации ткани к механическим нагрузкам и необходимым условием для нормального развития структуры эпителия, что также подтверждается экспериментальными данными в литературе [34; 35].

Миграция клеток в ткани

Клеточная миграция представляет собой ключевой процесс в развитии, регенерации тканей и метастазировании опухолей. В контексте эпителиальных листов наиболее часто наблюдаются два принципиально различных типа клеточного перемещения: мезенхимальный и амебоидный. Оба механизма характеризуются уникальными биофизическими особенностями, связанными с типом клеточного движения, взаимодействием с внеклеточным матриксом и организацией цитоскелета. Нами разработана модель миграции клеток в эпителиальной ткани, которая имитирует мезенхимальный и амебоидный тип миграции. Основные особенности мезенхимального типа миграции клетки заключаются в следующем: относительно медленная, но направленная скорость движения; низкая степень деформации тела клетки; сильная адгезия; клетка перемещается с помощью тяги, создаваемой ламеллоподиями на переднем краю; характер движения – равномерный. Схематическое изображение мезенхимального движения клетки представлено на рис. 17. В первый акт клетка выпячивает «голову», во второй акт – подтягивает «хвост». Для мезенхимального типа миграции характерны небольшие выпячивания относительно длины клетки. Для амебоидного типа миграции характерны следующие особенности: высокая и менее направленная скорость движения; высокая степень деформации тела клетки, возникновение блеб (выпячивания мембраны); слабая адгезия; клетка перемещается путём быстрой деформации собственного тела – формируются блебы с последующим сокращением хвоста; характер движения – пульсации. Схематическое изображение амебоидного движения клетки представлено на рис. 17.

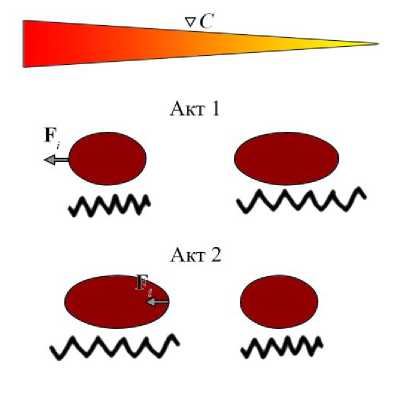
Рис. 17. Схематическое изображение мезенхимального и амебоидного типа миграции клетки. Чёрными пружинами проиллюстрировано, что происходит с клеткой на

Отметим, что для амебоидного типа миграции характерны большие выпячивания относительно длины клетки, чем в мезенхимальном случае. Кратко опишем нашу реализацию этих механизмов.

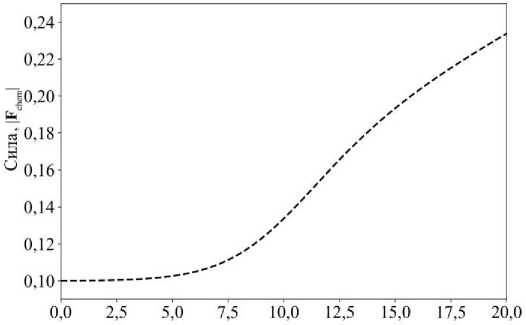
Начальные условия системы следующие. В момент времени t = 0 в системе находится 1817 шестиугольных клеток. Клетка с порядковым номером 827 имеет способность к движению и расположена у правой границы ткани (её координаты: X = 28,5; Y = 3,7). Именно за ней ведётся наблюдение. Вдоль всей левой границы задан поток химического сигнала, распространяющийся по ткани согласно уравнению (24). В случае мезенхимального типа миграции на вершины клетки действует химическая сила, определяемая логистической зависимостью:

Y C       , max i

F chem 1 + e- k ⁽ Ci - C H )             ,

которая описывает постепенное усиление чувствительности клетки к химическому сигналу с выходом на насыщение. В уравнении (28) γ max определяет чувствительность клетки к градиенту химического сигнала C , k – регулирует крутизну перехода между низкой и высокой чувствительностью, С H – пороговая концентрация, b – коэффициент смещения. На рис. 18 представлен график значений | F chem | от концентрации C i . Так, под действием силы клетка движется по градиенту химического сигнала и интеркалирует со своим микроокружением. В случае амебоидной миграции механизм перемещения реализован другим образом. Рассчитываем поток химического сигнала в наблюдаемой клетке. Сторона клетки, через которую поток положительный и максимальный, является ближней к источнику сигнала. С этой стороны происходит первый акт интеркаляции клетки, как проиллюстрировано на рис. 17, – акт 1, т.е. клетка выпячивается в сторону источника химического сигнала.

Концентрация, C

Рис. 18. Зависимость |Fchem| от концентрации Ci, представленная уравнением (28), для движущейся клетки в эпителиальной ткани. Значения силы и концентрации указаны в произвольных единицах каждом акте

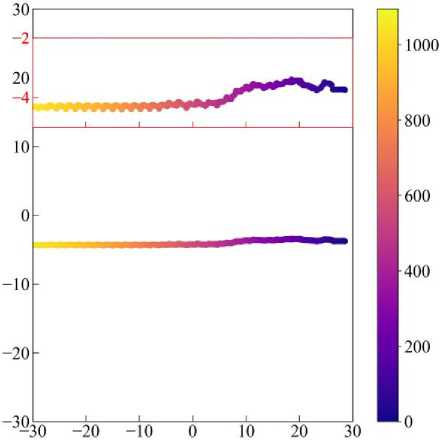
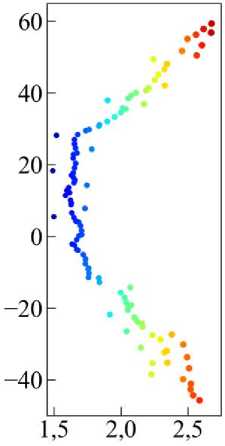
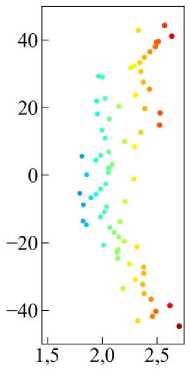
Рис. 19. Траектория перемещения клетки в случае мезенхимальной миграции, цветом отмечено время. На врезке показана траектория в увеличенном масштабе по вертикальной оси (выделено красным цветом).

Время указано в произвольных единицах

Затем происходит второй акт интеркаляции с противоположной стороны клетки: так она подтягивается, сохраняя свои размеры (рис. 17 – акт 2). За счёт таких выпячиваний и сокращений происходит ретракция клетки в ткани. Описанный механизм воспроизводит амебоидный тип миграции клетки в эпителии по градиенту химического сигнала [36].

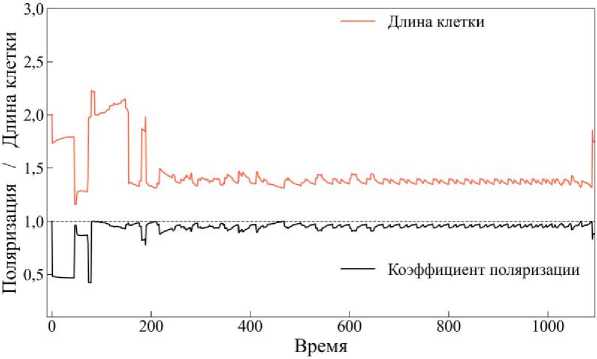
Рассмотрим мезенхимальный тип миграции подробнее. На рис. 19 показана траектория перемещения клетки. Видно, что перемещение происходит вдоль прямой, которая перпендикулярна потоку химического сигнала от источника с левой границы. Это говорит о том, что клетка имеет высокую степень поляризации, что подтверждается графиком на рис. 20, а (чёрная линия). Под поляризацией здесь понимается ориентация клетки в ткани относительно градиента химического сигнала. Коэффициент поляризации рассчитывается как значение cos( d , n ), где d – вектор, направленный от «хвоста» клетки к её «голове» и численно равный её длине, а n – вектор нормали к градиенту химического сигнала.

б

Рис. 20. Графики для случая мезенхимальной миграции: а – длины (красная линия) и поляризации (черная линия) клетки; б – скорости (красная линия) и фактора формы (чёрная линия) клетки. Зелёной пунктирной линией отмечено среднее значение скорости клетки <υ>, розовой пунктирной линией – среднее значение фактора формы <χ>.

Скорость, длина клетки и время указаны в произвольных единицах

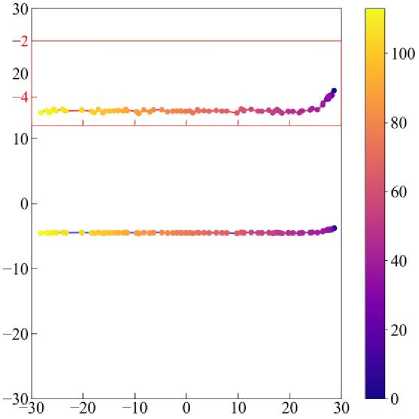
Рис. 21. Траектория перемещения клетки в случае амебоидной миграции, цветом отмечено время. На врезке показана траектория в увеличенном масштабе по вертикальной оси (выделено красным цветом).

Время указано в произвольных единицах

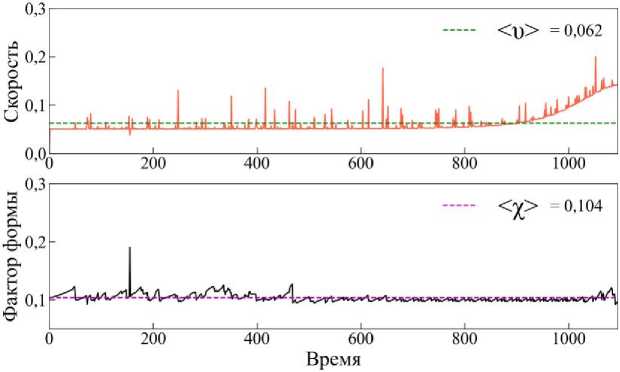
Таким образом значение cos(d, n) = 1 соответствует максимальной степени поляризации, т.е. клетка движется по нормали к градиенту сигнала. А значение cos(d, n) = 0 соответствует минимальной степени поляризации клетки. Из графика поляризации на рис. 20, а (чёрная линия) видно, что клетка поляризована в наибольшей степени на протяжении всего времени эволюции. А длина клетки |d|, начиная с момента времени t > 200, уменьшается и увеличивается примерно на одинаково малые значения (см. рис. 20, а (красная линия)). Это хорошо соответствует особенностям мезенхимального типа миграции. Интересную информацию также показывают и другие микроскопические параметры -скорость и и фактор формы клетки х (см. рис. 20, б). Движение происходит с небольшой скоростью, с редкими скачками, в основном в пределах и < 0,1. Средняя скорость <и> = 0,062 (см. рис. 20, б зелёная пунктирная линия), что соответствует плавному, равномерному перемещению. А среднее значение фактора формы <Х> = 0,104 (см. рис. 20, б розовая пунктирная линия), что близко к значению для правильного шестиугольника Х0 ~ 0,103.

б

Рис. 22. Графики для случая амебоидной миграции: а - длины (красная линия) и поляризации (черная линия) клетки; б - скорости (красная линия) и фактора формы (чёрная линия) клетки. Зелёной пунктирной линией отмечено среднее значение скорости клетки <и>, розовой пунктирной линией - среднее значение фактора формы клетки <х>.Скорость, длина клетки и время указаны в произвольных единицах

Это подтверждает, что клетка на протяжении всего времени сохраняет шестиугольную форму, характерную для ламеллоподиального механизма передвижения – без выраженных деформаций.

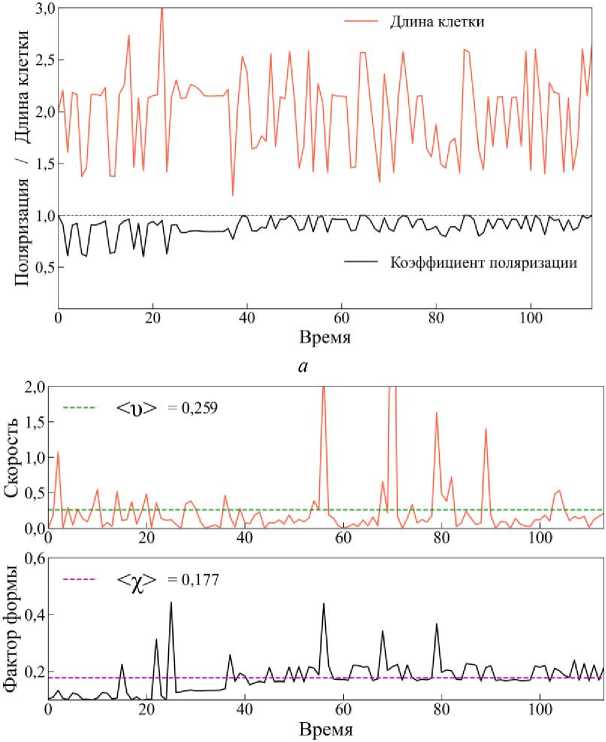
Для случая амебоидной миграции наблюдается иная картина. Из траектории перемещения клетки (рис. 21) видно, что время, за которое клетка преодолела такое же расстояние, как и в предыдущем случае, уменьшилось примерно в 10 раз. Траектория движения клетки осталась также перпендикулярной к источнику химического сигнала, но график коэффициента поляризации (см. рис. 22, а (чёрная линия)) показывает сильные отклонения от нормали, нежели в случае мезенхимальной миграции. Это свидетельствует о том, что клетка часто меняет свою траекторию движения по отношению к нормали градиента химического сигнала, что является характерным для амебоидного типа миграции. Длина клетки достаточно сильно меняется относительно начального значения (см. рис. 22, а (красная линия)), нежели в случае мезенхимальной миграции (см. рис. 20, а (красная линия)).

Средняя скорость <υ> перемещения клетки (см. рис. 22, б зелёная пунктирная линия) в этом случае больше, чем в случае мезенхимальной миграции, примерно в 4 раза, что указывает на высокую активность движения. Отмечается высокая вариабельность значений скорости с резкими пиками, достигающими значений более 2 единиц. Что касается динамики фактора формы клетки χ, характеризующего степень отклонения формы клетки от правильного шестиугольника, то картина следующая. Среднее значение <χ> = 0,177 превышает значение для регулярной формы χ 0 ≈ 0,103, что говорит о значительной деформации тела клетки. Регулярные колебания формы соответствуют пульсирующему, блебообразующему типу движения, характерному для амебоидной миграции.

Проведённый численный анализ показывает, что предложенная модель эффективно воспроизводит ключевые особенности амебоидной и мезенхимальной миграции клеток. Амебоидный тип характеризуется высокой скоростью и сильной деформацией клеточной формы, в то время как мезенхимальный – устойчивой