Исследование прочности монолитной бетонной крепи шахтного ствола в условиях переменных тепловых нагрузок

В настоящее время наиболее распространённым способом повышения прочности вертикальных шахтных стволов является искусственное возведение монолитного бетонного сооружения — крепи — по всему периметру ствола [1, 2]. Крепь служит для восприятия горного давления и тем самым предохраняет породные стенки от возможных обрушений [3].

Температурный режим бетонной крепи при длительной эксплуатации ствола определяется, прежде всего, температурой воздуха в нем [4, 5], которая может сильно варьироваться в зависимости от времени года. Одним из факторов резкого и значительного изменения температуры воздуха в стволе может стать реверсирование воздушной струи на руднике с целью проветривания. При запуске реверсивного режима проветривания происходит изменение направления воздушной струи во всех выработках рудника, в частности, в стволе, что при возникновении аварийной ситуации (например, пожара) даёт возможность кратчайшим путём через воздухоподающие стволы, надшахтные сооружения, подземные переходные

тоннели для движения горнорабочих, галереи и другое отвести вредные газы на поверхность и предотвратить отравление людей, застигнутых в шахте [6, 7]. Однако запуск реверсивного режима в зимнее время года может создать существенный перепад температуры между теплыми стенками крепи и холодным воздухом, нагнетаемым снаружи. Перепад может превышать 50°C (что наиболее характерно для рудников крайнего Севера). Это связано с тем, что вентиляционные стволы не оборудуются системами воздухоподготовки [8, 9], которые за счёт нагрева воздуха в теплообменных аппаратах позволили бы в случае реверсирования сохранить температуру воздуха в стволе. В данной ситуации отрицательный перепад температур может оказывать неблагоприятное воздействие на крепь шахтного ствола и вызывать в ней большие температурные деформации. О возможности такого явления упоминается в работах [10–12].

С учётом того, что монолитная бетонная крепь имеет низкую прочность на растяжение (на порядок ниже, чем на сжатие) [13], возникающие растягивающие напряжения при резком понижении температуры могут приводить к опасной ситуации её растрескивания или разрушения. Поэтому большую актуальность приобретает вопрос определения предельно допустимых изменений температуры в вертикальных шахтных стволах, при которых монолитная бетонная крепь сохраняет свою целостность и несущую способность.

Целью работы является исследование напряжённо-деформированного состояния (НДС) бетонной крепи и породного массива, окружающих шахтный ствол, и оценка прочности бетонной крепи при реверсировании воздушной струи в шахтном стволе в зимнее время года.

2.    Постановка задачи 2.1.    Концептуальная постановка

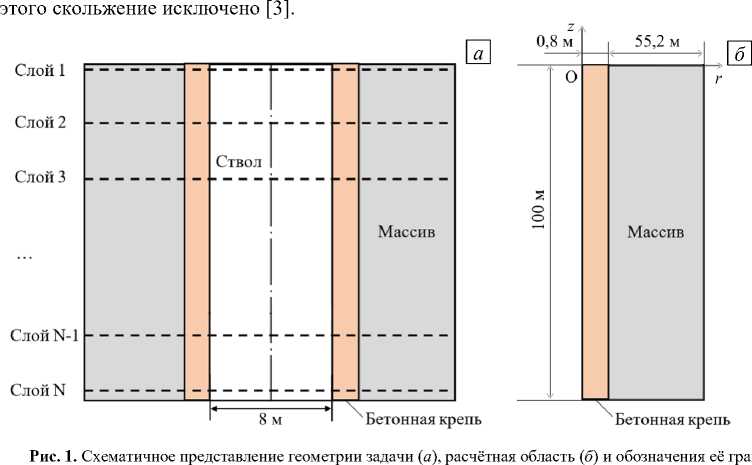
Рассматривается воздухоподающий ствол в форме цилиндра диаметром 8 м с окружающей его бетонной крепью и породным массивом на отрезке глубин от 0 до 100 м. Принимается, что массив и бетон являются изотропными и однородными. Данное допущение приемлемо как для использования по отношению к породному массиву, поскольку на выбранных глубинах он состоит из базальтовых пород с близкими теплофизическими и механическими свойствами, так и к бетону. Бетон считается изотропным и однородным материалом исходя из применяемой технологии возведения монолитной бетонной крепи с использованием опалубки (в заопалубочное пространство укладывается однородная бетонная смесь). Также, ввиду ограниченности исходных данных, полагается, что термодинамические свойства массива и бетона не зависят от температуры. Дополнительно учитывается условие полного сцепления между бетонной крепью и породным массивом на их границе. Полное сцепление на границе обусловлено тем, что поверхность контакта породного массива с бетонной крепью в действительности неровная, и вследствие

( в )

Указанные гипотезы позволяют использовать свойство пространственной симметрии и тем самым понизить пространственную размерность задачи до двух (Рис. 1). Все расчёты выполнены в цилиндрический системе координат O r ϕ z .

В задаче не учитывается влияние горизонтального давления пород. Это связано с тем, что в задаче рассматривается приповерхностный участок шахтного ствола сравнительно небольшой протяжённости, а также то, что на данных глубинах породный массив представлен относительно крепкими скальными породами (базальтами) со сравнительно низким коэффициентом бокового распора. В результате предварительных качественных оценок получено, что боковое давление на бетонную крепь [14] на порядок ниже напряжений, соответствующих температурным деформациям при перепаде 50°С. Таким образом, перепад температуры на границе бетонной крепи и породного массива является единственным значимым фактором, влияющим на НДС крепи и массива. Следует отметить, что это будет не так при анализе более глубоких участков ствола.

При расчёте распределения температуры в бетонной крепи и массиве учитывается кондуктивный теплоперенос в объёме пород и крепи ствола, теплообмен крепи и пород с атмосферным воздухом и теплообмен крепи с шахтным воздухом. Принимается, что в породном массиве не содержится влаги.

• 2.2.    Математическая постановка. Модель теплопереноса в бетонной крепи и породном массиве

Для расчёта теплопереноса в бетонной крепи и породном массиве используется уравнение баланса энергии в следующей форме:

д T д t

Здесь:   t — время, с; T - T ( r , z , t )  — температура,  °C;   a ( r ) -            — коэффициент

c(r)P(r)

температуропроводности, м2/с; X — коэффициент теплопроводности, Вт/(м^°С); c — удельная теплоёмкость, Дж/(кг^°С); р — плотность, кг/м3; r — радиальная координата, м; z — вертикальная координата, м.

В коэффициент температуропроводности заложена информация об изменении теплофизических свойств вдоль радиальной координаты при переходе из бетонной крепи в массив. Вследствие этого коэффициент задаётся с помощью приближённой функции Хевисайда H ( r ) :

a ( Г ) = а_с ( 1 - H ( Г ^- r cm ) ) + ^a m H ( Г ^- 1^ ) ,

H (r ) = 0,001 +

0,999

1 + exp ( - 5 r )

где a_c , a_m — коэффициенты температуропроводности бетонной крепи и породного массива соответственно (м²/с), r_cm — граница контакта бетонной крепи и породного массива. Такое представление функции Хевисайда необходимо для осреднения и сглаживания неровностей стенок ствола, которые образуются при его проходке. Подбор параметров функции основывается в работе на имеющихся данных о неровности стенок ствола в результате проходки: её средняя величина порядка ~0,1 м.

Уравнение (1) дополняется следующими начальными и граничными условиями:

д T дr д T дz

rin

T t =0 = T o ( z ) ,

= a s ⁽ T s ( z^T ) , T r - r out = T 0 ( z ) ,

^z = z air

-^T (z)-T),  —

X a^V ’    ’      дz

- 0.

^z = ^z - 100

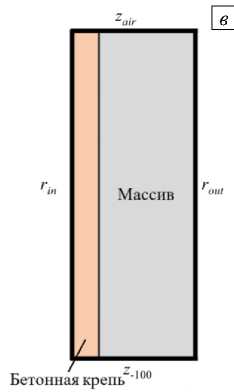
Здесь: T — температура бетонной крепи и породного массива в естественном залегании, °C; T ; T — температуры шахтного и атмосферного воздуха, соответственно, °C; a_s, a_o — коэффициенты теплопередачи через стенку ствола и через границу с атмосферным воздухом, Вт/(м² -° С); r_m — граница контакта бетонной крепи со стволом, м; r — внешняя граница породного массива, м; z — граница теплообмена с атмосферным воздухом, м; z ₁₀₀ — граница на глубине 100 м. Наглядное представление приведённых в (2) граничных условий можно видеть на рисунке 1 в .

Температура атмосферного воздуха задаётся в виде синусоидальной кривой сезонных колебаний от максимального значения +18,5°С в наиболее теплый период и до минимального -47°С, наблюдаемого в зимнее время:

T ( t ) -- 14,25 - 32,75sin

t       А п

-------------------- +--

365 ■ 24 ■ 60 ■ 60 )  2

Температура шахтного воздуха в нормальном режиме получена из решения сетевой задачи распределения расходов и температур воздуха в руднике, осуществлённого в аналитическом комплексе «Аэросеть» [15]:

T ( z ) = 19,84 - 0,0041 z .

Температура бетонной крепи и породного массива в естественном залегании представляется следующей зависимостью (исходя из экспериментальных данных о геотермии) [16]:

T _o ( z ) = - 2,53 - 0,024 z .

Описанная выше математическая модель теплопереноса и размеры расчётной области используются для нахождения температуры при нормальном режиме проветривания ствола. В случае реверсивного режима расчётная область при определении температуры имеет породный массив меньшей длины в радиальном направлении. Если для нормального режима длина породного массива принимается равной 55,2 м, то в реверсивном режиме длина массива составляет 2,3 м. Изменение расчётной области при моделировании реверсивного режима делается вследствие того, что время реверсирования невелико по сравнению со временем эксплуатации ствола в нормальном режиме проветривания, поэтому возмущения теплового поля не успевают пройти в массиве на большую глубину. На данной геометрии в дальнейшем и определяется НДС бетонной крепи и массива.

Помимо изменения расчётной области производится корректировка граничных условий: температура воздуха в стволе задаётся равной температуре атмосферного воздуха; на внешней границе массива фиксируется температура, которая получается из расчёта в нормальном режиме проветривания (последнее условие корректно по причине того, что изменение теплового поля не успеет достигнуть новой внешней границы массива). В остальном математическая модель теплопереноса для нормального и реверсивного режимов одинакова.

Теплофизические параметры, используемые при численном решении задачи теплопереноса, приведены в таблице 1.

Таблица 1. Теплофизические параметры

Параметр	Размерность	Значение
Диаметр ствола	м	8
Толщина бетонной крепи	м	0,80
Плотность породного массива, рт	кг/м3	2720
Удельная теплоёмкость породного массива, с	Дж/(кг∙°C)	850
Теплопроводность породного массива, Хт	Вт/(м∙°C)	1,95
Плотность бетонной крепи, рс	кг/м3	2400
Удельная теплоёмкость бетонной крепи, с	Дж/(кг∙°C)	880
Теплопроводность бетонной крепи, Хс	Вт/(м∙°C)	1,20
Скорость воздуха в стволе	м/с	9,12 (нормальный режим) 7,28 (реверсивный режим)
Коэффициент теплоотдачи на границе ствола, as	Вт/(м2∙°C)	13,75 (нормальный режим) 10,98 (реверсивный режим)
Коэффициент теплоотдачи на границе атмосферы, аа	Вт/(м2∙°C)	1,20
Время работы ствола в нормальном режиме	лет	6
Максимальное время работы ствола в реверсивном режиме	час	24

Таким образом, решая уравнение (1) вместе с граничными условиями (2) сначала для нормального режима проветривания, а после — для реверсивного режима, можно установить динамику температурного поля бетонной крепи и породного массива. В дальнейшем полученная информация используется для расчёта НДС в крепи и породном массиве.

• 2.3.    Математическая постановка. Деформационная модель бетонной крепи и породного массива

Задача определения НДС решается в двумерной осесимметричной постановке [17, 19]. Симметрия рассматривается относительно угловой координаты ф . В этом случае компоненты перемещений можно записать следующим образом:

u_r = u_r ( r , z ) ,     u _ф= 0, u z = U z ( r , z ) ,

где u , u , u — радиальные, угловые, вертикальные перемещения, м.

Связь деформаций и перемещений выражается позволяет воспользоваться уравнениями линейной осесимметричной постановки:

в предположении линейности деформаций, что теории упругости в рамках указанной выше

r

8 rr     л , dr

£ = 0,    £ r ф        ,          J

ur

£  = —   £ = — фф r       zz

• 1    (du .   du, A.

T I + T I ,    ^£ ф z ^{= 0}-

• 2    ^ dzd

где £_у ( i = ( r , z ) , j = ( r , z ) ) — компоненты тензора деформаций.

С учётом формул (4) и температурных напряжений можно записать уравнения состояния твёрдого тела в следующем виде:

° rr = । ^{K +} G G | ^£ rr ⁺ | ^K - G G । ( ^£фф ^{+ £} zz ) - ^{3 K aA} T ’ ° K + 4 G A £ фф + ^ K - 2 G A ( £ rr + £ zz ) - 3 к aA T , ° zz = ( K + 4 G A 8 zz ■ к - 2 G A ( 8 rr + 8 фф ) - 3 K aA T , □ = 0, □ = 1Gb , □ = 0. r ф        ,          rz             rz ,         ф z

При этом ° ( i = ( r , z ) , j = ( r , z ) ) — компоненты тензора напряжений K — объёмный модуль упругости, Па; G — модуль сдвига, Па; a — коэффициент линейного расширения, 1/°C; A T = T_reve-- T_normal — перепад температур, °C; T — температура расчётной области в момент окончания нормального режима проветривания, °C; T — температура расчётной области в заданный момент времени от начала действия реверсивного режима проветривания, °C.

Учитывая предположение о статическом состоянии бетонной крепи и породного массива, введённое в разделе 2.1, определить НДС крепи и пород можно с помощью уравнений равновесия:

8g 1 8g 8g □ — g u°rr +      rф + V° rz + rr '-'фф _ Q

8 r   r дф    d z       r

do rz . 1 ^д °ф z , ^д° zz , ° rz _=n

.

d r r дф d z r

Для упрощения решения уравнения (6) нужно переписать в перемещениях. Это легко сделать, если принять во внимание уравнения (4) и (5).

Поскольку при запуске реверсивного режима работы наибольший перепад температуры возникает на границе ствола (из-за быстрого охлаждения воздуха в стволе до атмосферной температуры), то изменение температурного поля в крепи и массиве будет происходить преимущественно в радиальном направлении. В таком случае можно предположить, что это скажется в основном на характере радиальной компоненты перемещений, и он обуславливается только радиальной координатой (данная гипотеза далее будет проверена). Тогда уравнения (3)–(5) можно представить в виде:

u_r = u_r ( r ) ,    u ф = 0,    u_z = 0;

d u _r

8 rr =      , dr

£ =0, r ф ,

ur фф         ,               ,

£ = 0, £ = 0;

rz      ,       ф z    ;’

° rr = ( K + 4 G Г rr Ч K - 2 G J S фф — 3 K ^aA T ,

°  = [K + j GJsw +^ K — з GJ srr — 3K«АT,

° zz = [ K — 2 G J(s rr +s,,)- 3 K аА T, °rф = 0,   °rz = 2Gsrz ,   °фz = 0.

На основании (9) уравнения равновесия редуцируются до одного:

Ra а —а

= 0.

^и ° rr | rr     фф

5 r       r

Для завершения формулировки модель дополняется граничными условиями отсутствия радиальных напряжений на стенке ствола и нулевыми радиальными перемещениями на внешней границе породного массива:

° rr L- г = 0, Ur\_r- г = 0. (11) ' ' in ' r out

Система уравнений (8)-(10) в итоге сводится к обыкновенному дифференциальному уравнению второго порядка относительно одной неизвестной функции ( u_r ) и двум граничным условиям (11), следовательно, задача является определенной.

Следует отметить, что изначально речь идёт о двумерной постановке задачи, согласно которой на рассматриваемую систему в общем случае необходимо, помимо условий (11), наложить два дополнительных граничных условия — нулевое касательное напряжение °_гф на границе r_in и нулевое угловое перемещение м_ф на границе r_out . Записанные выше соотношения (7)-(9) свидетельствуют, что данные условия выполняются.

Уравнение (10) вместе с граничными условиями (11) разрешается относительно перемещений, что позволяет найти поле компоненты u_r и далее, с помощью соотношений (8), (9) — поля компонент деформаций и напряжений.

Для оценки прочности бетонной крепи при воздействии на неё тепловых напряжений использовалась первая теория прочности — опасное состояние наступит в том случае, когда наибольшее по абсолютной величине нормальное напряжение превысит заданное допустимое значение [13]. Поскольку в данной работе бетонная крепь из-за понижения температуры в наибольшей степени испытывает растягивающие напряжения, то за величину допустимого напряжения берется максимальное значение неразрушающего напряжения на осевое растяжение бетона. Таким образом, критерий прочности можно записать в виде следующего неравенства:

°

max

n

‘ p ,

где Gm™ — наибольшее нормальное растягивающее напряжение, Па; R_p — допустимое напряжение на осевое растяжение, Па.

Если в бетонной крепи возникает область напряжений, при которых нарушается условие (12), то данная область считается областью её предразрушения. При этом не учитываются нелинейные процессы, которые могут иметь место в данной области. Также, если ширина зоны предразрушения превышает m % толщины бетонной крепи, то ситуация считается опасной для несущей способности крепи (величина параметра m будет конкретизирована далее).

В таблице 2 представлены механические параметры, используемые при расчёте НДС и оценке прочности бетонной крепи. Ввиду отсутствия проектных данных о физико-механических свойствах пород, в которых пройден ствол, объёмный модуль упругости и модуль сдвига у породного массива и бетона принимаются одинаковыми.

Далее с помощью описанной в разделе 2.1 модели теплопереноса и сформулированной в данном разделе деформационной модели проведено численное моделирование динамки температуры и НДС в бетонной крепи и массиве породы, в которой находится воздухоподающий ствол, и рассмотрено, как сказывается запуск реверсивного режима проветривания на прочности бетонной крепи. Для численного расчёта применялся метод конечных разностей. Подробнее о численной реализации задачи см. в разделе 3.

Таблица 2. Механические параметры бетонной крепи и породного массива

Параметр	Размерность	Материал
		Бетон	Породный массив
Объёмный модуль упругости, K	ГПа	34,40	34,40
Модуль сдвига, G	ГПа	37,50	37,50
Коэффициент теплового расширения, α	1/°C	1∙10-5	6,50∙10-6
Допустимое напряжение на осевое сжатие, R	МПа	1,56	–
Индикатор нарушения несущей способности крепи, m	%	50	–

• 2.4.    Построение деформационной модели бетонной крепи и породного массива в программном комплексе ANSYS

Деформационная модель бетонной крепи и массива строится на предположении, что перемещение бетонной крепи и массива происходит только в радиальном направлении (см. Раздел 2.2). Для проверки величины погрешности получаемого при этом решения дополнительно рассчитывалось НДС в программном комплексе ANSYS. Постановка задачи в ANSYS является двумерной, осесимметричной, с учётом того, что перемещения зависят как от радиальной, так и от вертикальной координаты. Поскольку считается, что бетонная крепь и породный массив находятся в квазистатическом состоянии, то для расчёта НДС использовался модуль Static Structural, в который подгружался внешний файл с полем температур, полученным из решения задачи теплопереноса методом конечных разностей.

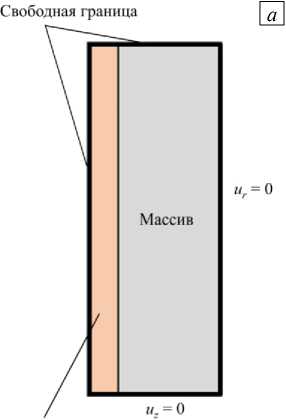
Бетонная крепь

Рис. 2. Деформационная модель в граничных условий (а); вид расчётной сетки (б)

ANSYS: схематичное изображение

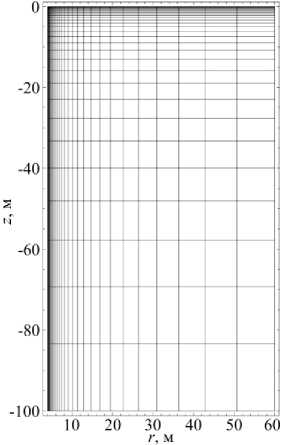
Рис. 3. Пример расчётной сетки для моделирования теплопереноса

Задавались следующие граничные условия: поверхности контакта бетонной крепи со стволом и с атмосферным воздухом считались свободными; поверхность контакта породного массива с атмосферным воздухом считалась свободной; на горизонте –100 м нормальная компонента перемещений приравнивались нулю (см. Рис. 2 а ). Механические свойства бетона и породного массива брались из таблицы 2.

3.    Численная реализация

Динамика теплопереноса и НДС определялась на основе уравнений (1), (2), (7)–(11); для их решения использовался метод конечных разностей. Дискретизация по времени проводилась по неявной схеме Эйлера. В задаче теплопереноса расчётная область покрывалась неравномерной регулярной сеткой со сгущением вблизи границы контакта бетонной крепи и ствола, а также окрестности границы теплообмена с атмосферой (см. Рис. 3). При нахождении НДС сетка была равномерной. Для реализации метода конечных разностей был написан специальный модуль в пакете компьютерной алгебры Wolfram Mathematica.

При расчёте НДС в программном комплексе ANSYS область решения задачи разбивалась нерегулярной и неравномерной сеткой из треугольных элементов со сгущением вблизи границы контакта бетонной крепи и ствола и вблизи границы с атмосферой (см. Рис. 2 б ).

В таблице 3 приведены числовые параметры, используемые при расчёте с помощью модуля, созданного в Wolfram Mathematica, и в программном пакете ANSYS. Видно, что при вычислениях в Wolfram Mathematica требуется гораздо меньшее количество узлов для решения задачи теплопереноса, чем при определении НДС. Это является следствием того, что для расчёта поля температуры используется неравномерная сетка со сгущением в областях с наибольшими градиентами температуры. Это позволило значительно сократить количество узлов в применяемой сетке.

Таблица 3. Параметры численной реализации

Параметр	Размерность	Значение
Задача теплопереноса
Начальный размер шага по радиальной координате	м	0,050 (нормальный режим) 0,001 (реверсивный режим)
Начальный размер шага по вертикальной координате	м	0,050
Коэффициент увеличения шага по радиальной координате	%	5
Коэффициент увеличения шага по вертикальной координате	%	10
Шаг по времени	час	1051.2 (нормальный режим) 0,48 (реверсивный режим)
Общее количество узлов	–	4788 (нормальный режим) 3306 (реверсивный режим)

Определение НДС (Wolfram Mathematica)

Шаг по радиальной координате	м	0,0006
Шаг по вертикальной координате	м	10
Общее количество узлов	–	50000

Определение НДС (ANSYS)

Минимальный характерный размер сетки	м	0,02
Максимальный характерный размер сетки	м	0,08
Общее количество элементов	–	141446

4.    Результаты

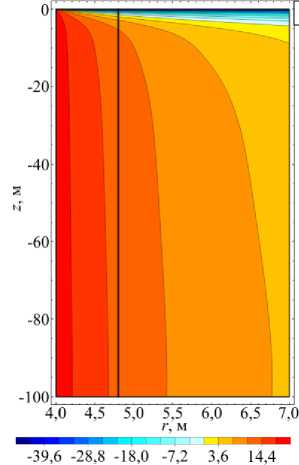
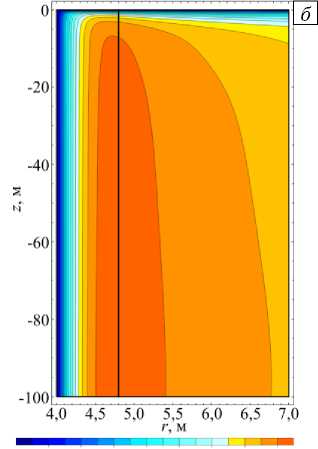
По результатам численных расчётов температуры бетонной крепи и массива установлено, что до начала реверсирования воздуха в стволе наибольшее значение температуры наблюдалось на границе их контакта со стволом и равнялось 20°C (см. Рис. 4 а ). После начала реверсирования воздуха на границе контакта ствола с крепью из-за интенсивного теплообмена, обусловленного высокой скоростью воздуха в стволе, в течение очень короткого времени устанавливается температура атмосферного воздуха (см. Рис. 4 б ).

39,6 -28,8 -18,0 -7,2 3,6 14,4

Рис. 4. Поле температуры бетонной крепи и породного массива (вертикальная линия – граница их контакта): через 6 лет после начала работы ствола при нормальном режиме проветривая ( а ) и спустя 24 часа после запуска реверсивного режима проветривания ( ( б )

По полученным температурным полям при нормальном и реверсивном режимах проветривания были рассчитаны перепады температуры при реверсировании воздуха в стволе через различные промежутки времени после начала реверсирования. Данные вычислений только для области бетонной крепи приведены на рисунке 5. Из-за того, что после запуска реверсирования на границе контакта крепи со стволом устанавливается температура атмосферного воздуха, возникает значительный перепад температуры, наибольшее значение наблюдается вблизи границы ствола с крепью. Максимально достигаемое значение перепада температур по абсолютной величине равняется 67°C. Во всей расчётной области перепад температур имеет отрицательные значения, то есть происходит только охлаждение бетонной крепи и массива. Также полученные поля свидетельствуют, что фронт перепада температуры распространяется преимущественно вдоль радиального направления с незначительными отклонениями от вертикали вблизи границы контакта с атмосферой.

Далее полученные перепады температуры использовались для расчёта напряжений в бетонной крепи и массиве в Wolfram Mathematica. На рисунке 6 показаны результаты после 24 часов реверсирования. Положительный знак напряжений означает, что они растягивающие.

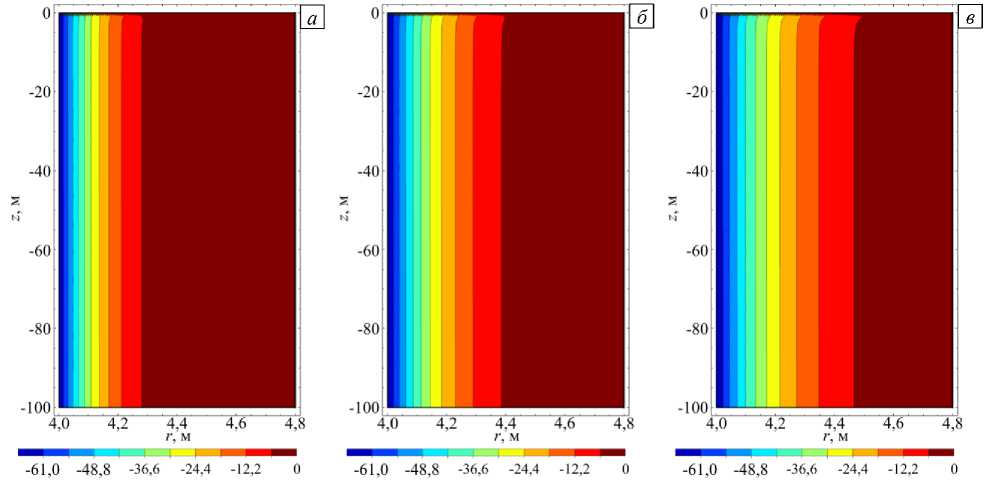
Рис. 5. Поле перепада температуры в бетонной крепи при реверсивном режиме проветривания в различные моменты времени: через 8 часов ( а ); через 16 часов ( б ); через 24 часа ( в )

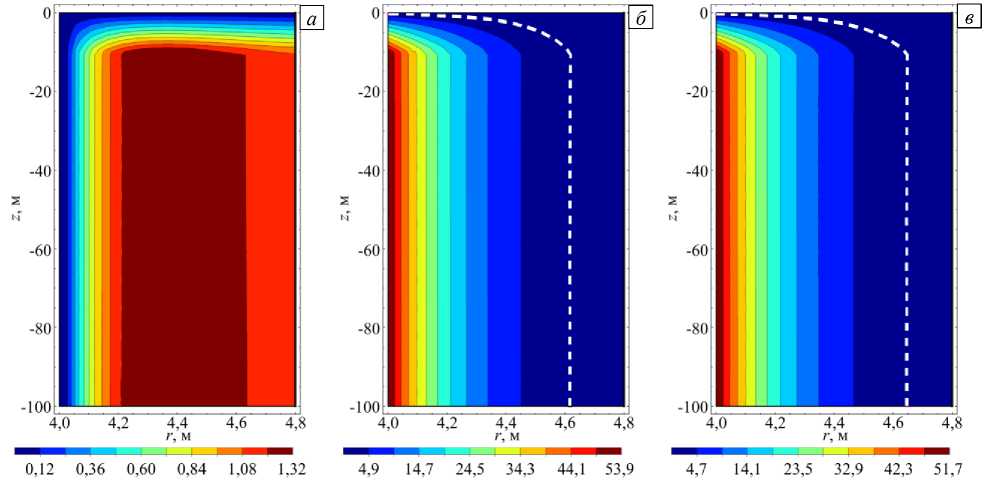
Рис. 6. Поля напряжений (МПа) в бетонной крепи после 24 часов реверсивного проветривания: радиальных σ  (а), угловых σ  (б) и вертикальных σ  (в); штриховой линей обозначена граница зоны предразрушения

Из анализа полей на рисунке 6 следует, что после 24 часов реверсирования воздуха в стволе все напряжения, возникающие в расчётной области, являются растягивающими. При сравнении компонент можно видеть, что максимальное значение радиальных напряжений ( σ ) на порядок ниже максимальных значений угловых ( σ ) и вертикальных ( σ ) напряжений. Кроме того, поля угловых и вертикальных напряжений практически совпадают друг с другом. В связи с этим возникает вопрос: можно ли данные напряжения считать полностью эквивалентными и любое из них принимать за максимальное при оценке прочности бетонной крепи по условию (12)? Для ответа на данный вопрос была построена граница зоны предразрушения для угловых (см. Рис. 6 б ) и вертикальных (см. Рис. 6 в ) напряжений. В итоге зона предразрушения в поле вертикальных напряжений оказывается на 4 см шире, чем в поле угловых напряжений.

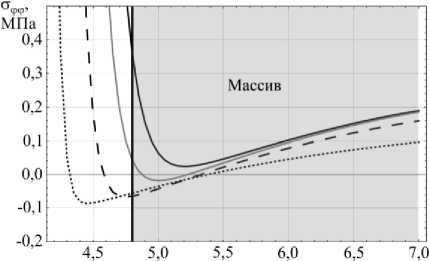
В дополнение проведен более детальный анализ графиков напряжений вдоль радиальной координаты на некоторой глубине (см. Рис. 7). Из рисунка видно, что угловые напряжения при приближении к границе контакта крепи и массива снижается быстрее, чем вертикальные. Кроме того, если вертикальные напряжения при любой длительности реверсирования выходят на асимптоту, то у угловых напряжений при времени реверсирования от 2 до 8 часов можно наблюдать локальные области со сжимающими напряжениями. Таким образом, на основании данного анализа было решено принимать за максимальное напряжение при оценке прочности бетонной крепи напряжение, действующее в вертикальном направлении.

г, м

Рис. 7. Зависимость угловых и вертикальных напряжений на

24,      16,      8,      2

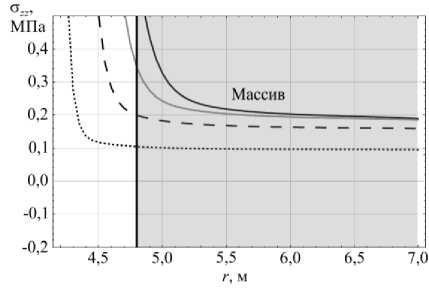
глубине -50 м от длительности реверсирования, час:

Далее НДС бетонной крепи и массива, рассчитанные в Wolfram Mathematica, сравнивались с результатами, вычисленными в ANSYS. Графики напряжений сопоставлялась для длительности реверсирования 24 часа (см. Рис. 8). По кривым на рисунках 8 б , в можно видеть, что угловые

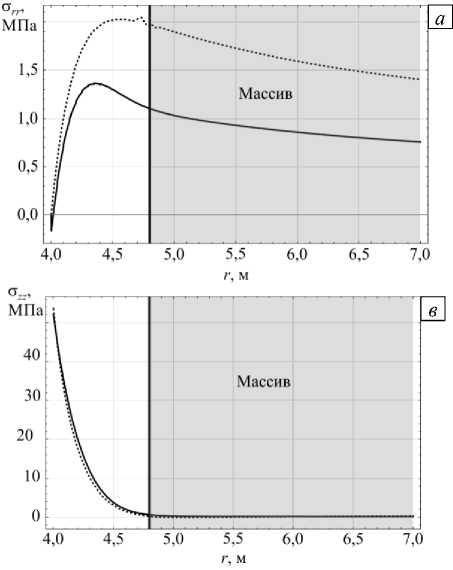
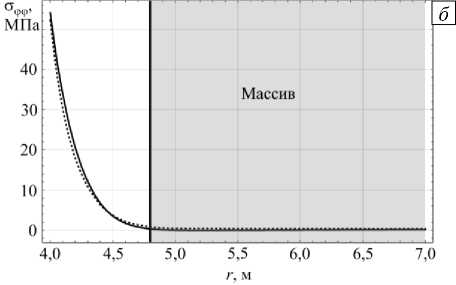
Рис. 8. К сравнению графиков напряжений в бетонной крепи и породном массиве на глубине -50 м, построенных по данным расчёта в Wolfram Mathematica (сплошная линия) и ANSYS (пунктирная линия): радиальные напряжения ( а ); угловые напряжения ( б ); вертикальные напряжения ( в )

и вертикальные напряжения, полученные при расчётах в Wolfram Mathematica, практически совпадают с найденными в ANSYS. При сравнении радиальных напряжений (см. Рис. 8 а ) между двумя моделями наблюдаются значительные различия. Однако различия в большей степени носят количественный характер, чем качественный. Значения радиальных напряжений, полученные в ANSYS, в среднем в 1,8 раз выше, чем значения, рассчитанные в Wolfram Mathematica.

Таким образом, в условиях решаемой задачи можно пользоваться упрощённой моделью для расчёта НДС, описываемой уравнениями (7)–(11), поскольку получаемые на её основе вертикальные напряжения (используемые при оценке прочности бетонной крепи) качественно и количественно практически совпадают с данными расчёта с использованием полноценной двумерной осесимметричной постановки.

В итоге по полученным результатам построен график зависимости ширины зоны предразрушения от времени реверсирования и различной температуры воздуха в стволе (см. Рис. 9). В результате анализа рисунка 9 установлено, что ширина зоны предразрушения нелинейно зависит от длительности реверсирования. При этом уже при малой длительности реверсирования (не более 1 часа) её ширина может превышать 0,1 м при всех рассмотренных значениях температуры воздуха. С увеличением времени реверсирования в значениях ширины зоны предразрушения для разных температур воздуха в стволе различия нарастают.

Поскольку в данном исследовании принимается, что несущая способность бетонной крепи нарушается, если ширина зоны предразрушения достигает m = 50% ширины бетонной крепи в радиальном направлении (0,4 м в данной задаче), то в дополнение к графику на рисунке 9 был построен график зависимости допустимой продолжительности реверсирования воздушной струи от температуры воздуха в стволе, при которой состояние бетонной крепи достигает 50%-ного предразрушения (см. Рис. 10).

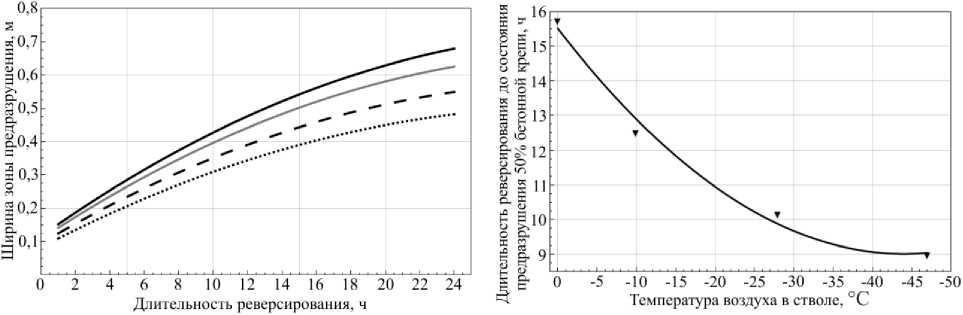
Рис. 9. Зависимость ширины зоны предразрушения от времени реверсирования воздуха в стволе и его температуры, °C: -47, -28, -10, 0

Рис. 10. Зависимость длительности реверсирования до состояния 50%-ного предразрушения бетонной крепи от температуры воздуха в стволе

Полученный график свидетельствует: длительность реверсирования до состояния 50%-ного предразрушения бетонной крепи с увеличением температуры растёт нелинейно (в данном случае — по гиперболическому закону); с ростом температуры воздуха в стволе от -47 до 0°C необходимое время реверсирования для доведения бетонной крепи до состояния 50%-ного предразрушения увеличивается на 57%.

4.    Заключение

Основные результаты данной работы:

• 1.    Построены двумерная термодинамическая и деформационная модели шахтного ствола, позволяющие рассчитать НДС бетонной крепи и породного массива по фактору температуры. Термодинамическая модель включает: кондуктивный теплоперенос в крепи и массиве пород, теплообмен крепи с воздухом в стволе; теплообмен крепи и породного массива с атмосферным воздухом; сезонные колебания атмосферной температуры; вариацию температуры при реверсировании воздуха в стволе. В деформационной модели принимается в расчёт только влияние перепада температуры на напряжённо-деформированное состояние бетонной крепи и породного массива. Горизонтальное давление пород не учитывается вследствие того, что рассматривается участок шахтного ствола вблизи поверхности, его протяжённость вглубь относительно невелика, а породный массив представлен крепкими скальными породами со сравнительно низким коэффициентом бокового распора. Также не учитывается боковое давление на бетонную крепь, поскольку в результате предварительной оценки величина бокового давления на порядок ниже величины напряжений, соответствующих температурным деформациям при перепаде 50°С.

• 2.    Результаты расчёта НДС бетонной крепи по фактору температуры при реверсировании воздуха в шахтном стволе в зимнее время года показали, что бетонная крепь в большей степени испытывает растягивающие напряжения, а максимальные абсолютные величины напряжений возникают в основном в вертикальном направлении.

• 3.    Принятое при оценке прочности бетонной крепи с учетом лишь температурных напряжений предположение о зависимости перемещений только от радиальной составляющей и отсутствии перемещений вдоль угла и вертикали допустимо. Однако стоит иметь в виду, что в этом случае значение радиальных напряжений снижается в среднем в 1,8 раза.

• 4.    С ростом температуры воздуха в стволе ширина зоны предразрушения бетонной крепи уменьшается. Но наибольшее влияние на ширину зоны предразрушения оказывает одновременное увеличение как температуры, так и длительности реверсирования.

• 5.    Получена нелинейная зависимость от температуры воздуха в стволе длительности реверсирования до состояния 50%-ного предразурешения крепи. Согласно ей при увеличении температуры воздуха в стволе от -47 до 0°C длительность реверсирования до состояния предразрушения бетонной крепи на 50% увеличивается на 57%.