Исследование прогнозирования производительности многофазной системы массового обслуживания методом машинного обучения

Многофазные системы массового обслуживания - это системы, в которых заявки обслуживаются последовательно на многих этапах. Системы такого типа адекватно моделируют компьютерные сети с линейной топологией. Например, в [1-4] приведено применение многофазной системы для моделирования таких сетей. Производительные характеристики системы массового обслуживания можно вычислить, решив ее систему уравнений баланса, однако для сложных систем это непрактично, поскольку потребность в вычислительных ресурсах растет экспоненциально. Поэтому на практике системы массового обслуживания исследуются методом имитационного моделирования (Монте-Карло). В последнее время появилось много исследований [5-9], в которых изучались идеи использования подхода машинного обучения для оценки производительности системы массового обслуживания.

Распространенным явлением в компьютерных сетях является ретрансляция, то есть повторная отправка пакетов, потерянных во время передачи данных. В теории массового обслуживания это явление моделируется очередями с орбитой. Подробный обзор работ

(с) Данг М.К., 2024

• (с) Федеральное государственное автономное образовательное учреждение высшего образования

  «Московский физико-технический институт (пациопальпый исследовательский университет)», 2024

2.    Модель системы массового обслуживания

на эту тему можно найти в [10]. Однако существует относительно немного работ, в которых изучалась многофазная система массового обслуживания с орбитой (которая является общей для всех станций в системе) [11-13].

В предыдущей статье мы исследовали многофазную систему массового обслуживания с орбитой, пуассоновским входным потоком и экспоненциально распределенным временем обслуживания [14]. Для такой системы массового обслуживания использование аналитического метода возможно только в случае очень малого количества фаз и размера буферов. Кроме того, среднее время отклика системы не может быть рассчитано аналитическим методом. С другой стороны, метод имитационного моделирования может дать результаты для любого случая, однако имитация системы с большим количеством фаз выполняется медленно. Поэтому в этой статье мы исследуем возможность использования методов машинного обучения для оценки производительности многофазной системы массового обслуживания, описанной в нашем предыдущем исследовании.

Мы рассматриваем сеть, состоящую из N станций, где N — 1 обычных станции соединены в линейной топологии, а одна станция соединена со всеми обычными станциями. Мы обозначаем эту специальную станцию как станцию 0, а обычные станции - как станции от 1 до N — 1. Каждая станция г имеет сервер с экспоненциально распределенным временем обслуживания с параметром ц и буфер с ограниченным размером ki. Пуассоновский поток с параметром А поступает в систему на станции 1, последовательно обслуживается станциями с 1 по N и выходит из системы на станции N — 1. Например, на рис. 1 показана схема системы с п станциями.

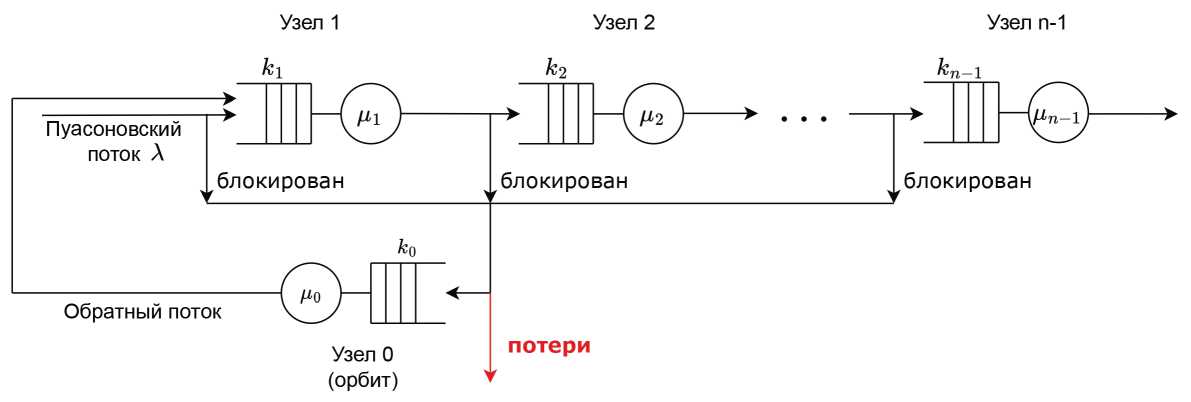
Рис. 1. Схема многофазной системы с орбитой

Если буфер на станции г заполнен, входящие пакеты на станции г отправляются на станцию 0. Если буфер на станции 0 также заполнен, то пакеты теряются. После завершения ожидания на станции 0 пакеты отправляются обратно на станцию 1, если в буфере на станции 1 есть свободные места, в противном случае они по-прежнему продолжат ожидать. Это отличается от системы в [14], где пакеты всегда отправляются обратно на станцию 1 независимо от того, заполнен буфер станции 1 или нет.

Пусть X = (А,цо,ко,Ц1 ,ку...,цу-уку -1) - параметры, представляющие систему массового обслуживания, а у - показатель производительности системы, который необходимо оценить, например, среднее времени отклика или среднюю вероятность потери пакетов. Наша цель - обучить модель машинного обучения, которая принимает входной X и возвращает соответствующий выходной у.

• 3.    Нейронные сети для прогнозирования производительности системы массового обслуживания

  3.1.    Обучающие данные

Чтобы сгенерировать синтетические данные для обучения нейронных сетей, мы провели имитации системы массового обслуживания со случайными параметрами:

• •    N (число станций) - дискретная равномерно распределенная случайная величина на интервале [2,16].

• •    X, щ - непрерывная равномерно распределенная случайная величина на интервале (0,1024].

• •    к{ - дискретная равномерно распределенная случайная величина на интервале [0,16].

Для каждого случайного параметра X мы получили обратную величину среднего времени отклика у системы массового обслуживания из имитационной программы. Причина, по которой мы выбираем обратную величину, заключается в том, что она имеет одинаковую размерность с X и ц; (пакетов в секунду). Это привело к тому, что результаты обучения стали намного лучше, чем без него.

Затем мы собрали и разделили результаты имитации на различные наборы данных:

• •    Datasetl28k: Датасет из 131072 точек данных (Х,у) для целей обучения.

• •    Test32k: Датасет из 32768 точек данных (X, у) для целей проверки.

Кроме того, мы подготовили два небольших набора неслучайных данных:

• •    Samplel: Датасет из 11 точек данных (X,у), где все X и ц; равны 1, а к; изменятся от 0 до 10.

• •    Sample512: Датасет из 11 точек данных (X,у), где все X и ц равны 512, а к; изменятся от 0 до 10.

3.2.    Модель многослойного перцептрона

Эти два набора данных теоретически одинаковы, поскольку умножить все Хи ц; наш раз -значит разделить среднее время отклика на т раз. Однако Sample512 можно рассматривать как среднюю величину обучающих данных, a Samplel как выброс.

Многослойный перцептрон (MLP) - это классическая модель нейронной сети в области глубокого обучения. Ее структура, состоящая из входного слоя, одного или нескольких скрытых слоев и выходного слоя, позволяет моделировать сложные нелинейные взаимосвязи между входами и выходами. Это делает ее универсальным инструментом для задач регрессии или классификации. Кроме MLP, существуют и другие классические методы машинного обучения, такие как метод опорных векторов (SVM), градиентный бустинг, случайный лес и т.д. SVM имеет квадратичную временную сложность по отношению к количеству данных, поэтому в нашем случае (более 100 тысяч точек данных) процесс обучения был слишком долгим, чтобы быть практичным. Используя библиотеку scikit-learn, мы провели обучение методами градиентного бустинга и случайного леса, однако их результаты были ненамного лучше, чем при использовании нейронных сетей (табл. 2). Недавно появилась новая форма нейронных сетей, называемая сетями Колмогорова - Арнольда (KAN) [15]. В отличие от MLP, где изучаемыми параметрами являются веса линейных преобразований, в KAN изучаемыми параметрами являются нелинейные функции активации. Однако, поскольку К AN является новым методом, ему не хватало стабильной реализации в библиотеках программирования по сравнению с другими классическими и популярными методами машинного обучения.

Поэтому наше исследование началось с модели MLP, показанной на рис. 2. Это MLP модель с 16 скрытыми слоями, каждый из которых состоит из 256 нейронов. Поскольку нейронная сеть MLP принимает только ввод фиксированного размера, то для значения X, которое имеет число станций N <  16, мы добавим к нему 0 (например, если N = 5, то ц_г = 0,ki = 0 для всех г = 5,..., 15).

Скрытые слои (16 слоев)

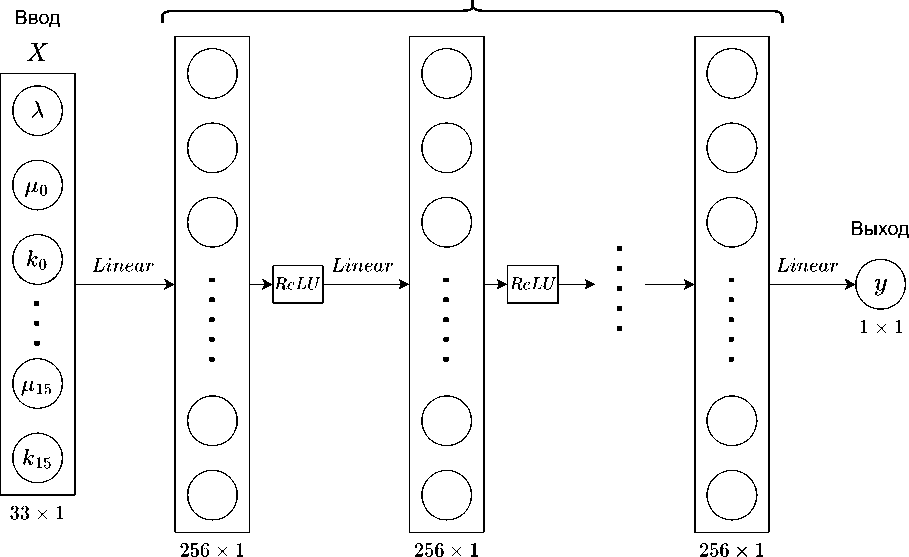
Рис. 2. Схема нейронной сети MLP

Нейронная сеть была реализована с использованием библиотеки PyTorch и обучалась на видеокарте NVIDIA RTX 3070 Ti. Параметры обучения выбраны следующим образом: числовой формат модели - FP32, скорость обучения lr = 10^-4, время обучения epochs = 1024. Мы обучили три модели, одна из которых использовала критерии среднеквадратичной ошибки (MSE), другая - критерии средней абсолютной ошибки (LILoss), и последняя -критерии HuberLoss с 5 = 0.5. HuberLoss по определению является комбинацией MSE и LILoss: п

HuberLoss(y,y) = ^^/д i=1

/ = |0,5(й - уг)2,         если\уг - уг\ <5, г     [5(\уг - уг\ - 0,55),   если\уг - уг\ > 5.

После завершения обучения мы проверяем предсказательную способность моделей на наборах данных Test32k, Samplel и Sample512 (табл. 1). Обратите внимание, что из-за отсутствия модуля ReLU на последнем слое сети прогнозирования моделей могут принимать отрицательные значения. Поэтому перед выполнением сравнения мы изменили все отрицательные прогнозы на 0.

Из таблицы 1 видно, что модели работали не очень хорошо. Наилучший результат был получен в наборе данных Sample512, где средний процент ошибок всех моделей (MSE, LILoss и HuberLoss) составил 35,42%; 32, 94% и 45, 98% соответственно. Поэтому мы предложили модифицированную структуру нейронной сети, которая позволила бы добиться лучших результатов прогнозирования.

Результаты проверки модели MLP

Таблица 1

Критерий обучения	Test32k		Samplel		Sample512
	Средняя ошибка(%)	*(%)	Средняя ошибка(%)	^(%)	Средняя ошибка(%)	^(%)
MSE	128,52	2152,19	12450,42	28019,28	35,42	15,72
LILoss	110,51	2763,02	15163,80	11222,45	32,94	22,81
HuberLoss	113,87	3275,21	10907,50	17916,92	45,98	15,76

Т а б л и ц а 2

Результаты проверки других методов машинного обучения

Метод обучения	Test32k		Samplel		Sample512
	Средняя ошибка(%)	^(%)	Средняя ошибка(%)	^(%)	Средняя ошибка(%)	^(%)
Градиентный бустинг	650,38	8884,92	136298,59	27461,09	46,22	5,63
Случайный лес	152,97	4052,79	9603,09	1425,89	50,89	12,86

3.3.    Предложенная модель нейронной сети

В отличие от модели MLP, где весь входной слой X связан с первым скрытым слоем, в нашей модели мы разделили X на 15 частей: Вход1 = (X, го,ко, тДД Вход2 = (Д2Д2), ..., Вход15 = (г15, к15). Вход1 связан с первым скрытым слоем. Затем первый скрытый слой объединяется с Входом2, становясь входом для третьего скрытого слоя, и так далее (рис. 3). Эта модель напоминает процесс роста исследуемой системы массового обслуживания, когда сначала у нас есть только одна станция и орбита, а затем мы постепенно добавляем в систему новую станцию.

Мы снова обучили модифицированную нейронную сеть с теми же параметрами обучения, что и в предыдущем разделе, и получили результаты проверки (табл. 3). Очевидно, что предложенная модель показала значительно лучшие результаты, чем модель MLP. Более того, мы заметили, что модель, обученная с использованием критериев LILoss, также показала значительно лучшие результаты, чем модель, обученная с использованием MSE. Причина в том, что наши выходные значения у находятся в интервале от очень малых до очень больших значений, но MSE отдает приоритет большим значениям из-за своей квадратичной природы. Это приводит к тому, что модель, обученная с использованием MSE, работает хуже, чем модель с LILoss. Удивительно, хотя результат модели с HuberLoss был хуже, чем LILoss в Teest32k, HuberLoss был значительно лучше, чем LILoss в Sample512.

Т а б л и ц а 3

Результаты проверки новой модели

Критерий обучения	Test32k		Samplel		Sample512
	Средняя ошибка(%)	^(%)	Средняя ошибка(%)	^(%)	Средняя ошибка(%)	^(%)
MSE	51,79	937,16	7398,59	18257,48	39,10	7,30
LILoss	24,30	570,60	1409,20	3676,93	26,75	8,45
HuberLoss	32,35	729,39	1617,98	1509,40	15,72	9,14

Этот вывод привел нас к проведению эксперимента с критерием, который более устой- чив к выбросам, чем LILoss, то еств MSLE (среднеквадратичная логарифмическая ошибка):

MSLE(у, у) = ][2ln(1 + yi) - ln(1 + у^ i=1

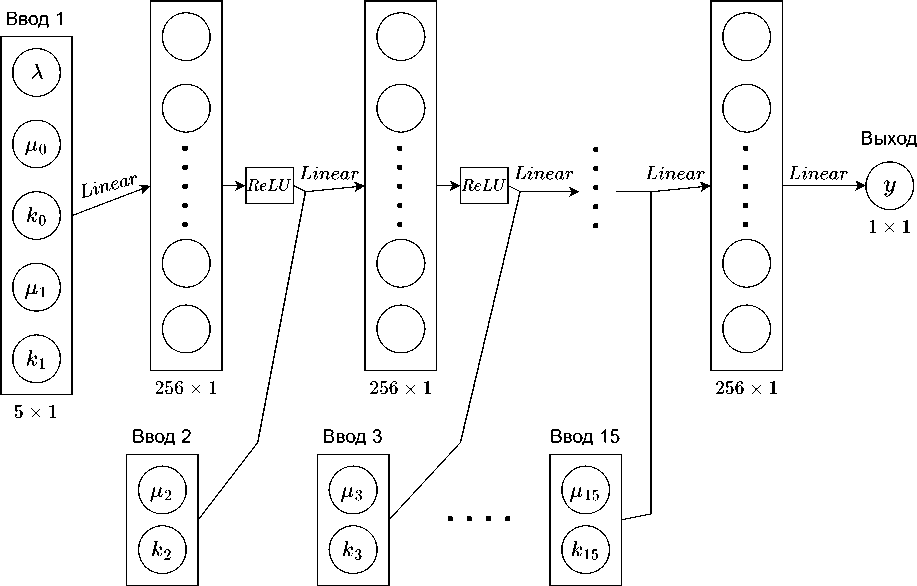
2x1           2x1              2x1

Рис. 3. Схема модифицированной нейронной сети

Посколвку функция логарифмирования не определена при отрицательных значениях, мы внесли небольшую модификацию в структуру нейронной сети на рис. 3, добавив модуль ReLU перед выходным слоем у. Таким образом, функция MSLE всегда определялась в процессе обучения. Как и ожидалось, из табл. 4 видно, что модель, обученная с MSLE, в целом лучше, чем с LILoss, однако для датасета Sample512 она показала те же результаты (27, 65 и 26, 75). Чтобы еще больше улучшить результаты, мы заново обучили модель, применив следующий режим изменения скорости обучения:

10-4,        если epoch < 192,

1г

< 10-5,        если 192 < ероch < 512,

Д,5 х 10-5, если epoch > 512.

Использование режима изменения скорости обучения позволило добиться наилучших результатов (табл. 4). Однако даже в этом случае прогноз для Samplel оставался неприемлемым (средняя ошибка = 257,14%). И с учетом того факта, что стандартное отклонение при проверке датасета Test32k все еще очень велико ( a = 218, 85%), мы можем заключить, что модель не смогла обработать случаи с выбросами. Улучшение возможностей модели для учета исключительных случаев станет предметом дальнейших исследований.

Хотя результаты нейросетевых моделей неточны по сравнению с результатами имитационного моделирования, скорость выполнения нейронной сети значительно выше, чем скорость выполнения имитационного моделирования. Например, на компьютере с процессором Xeon Е2680 V4 потребовалось 76 часов (в одном потоке), чтобы сгенерировать Datasetl28k путем имитационного моделирования. С другой стороны, нейронной сети на том же компьютере потребовалось всего 7 секунд, чтобы завершить предсказание для Datasetl28k. Это разница на пять порядков.

Т а б л и ц а 4

Результаты проверки новой модели, обученной по критериям MSLE

	Test32k		Samplel		Sample512
	Средняя ошибка(%)	^(%)	Средняя ошибка(%)	^(%)	Средняя ошибка) %)	^(%)
Неизменная скорость обучения	18,79	454,30	428,06	361,99	27,65	5,74
Измененная скорость обучения	12,27	218,85	257,14	336,82	9,16	3,91

4.    Заключение

В этой статье мы экспериментировали с использованием моделей нейронных сетей для прогнозирования производительности многофазной системы массового обслуживания с орбитой и обратной связью. Мы показали, что прямое использование модели многослойного персептрона без внесения изменений не даст хороших результатов даже при большом количестве нейронов и слоев. Поэтому мы предложили специфическую структуру нейронной сети и параметры обучения, которые за короткое время обучения (epochs = 1024) и небольшое количество обучающих данных (128 тыс.) позволили создать модель с хорошей способностью к прогнозированию. Однако наша модель по-прежнему не справлялась с предсказанием некоторых случаев в датасете, поэтому в будущем мы будем стремиться улучшить модель нейронной сети для таких случаев.