Исследование пространственно-временной структуры поля электромагнитного импульса с крутым фронтом при распространении в вакууме

Целью настоящей работы является исследование эволюции пространственно-временной структуры поля импульса с крутым передним и задним фронтом при распространении в вакууме. Обращено внимание на процессы установления и спада поля импульса. Из-за специфики исследуемых процессов (быстрота изменения во времени) не применим традиционно используемый в оптике метод медленно меняющихся амплитуд [1]. Исследование проводилось на основе решения дифракционного интеграла Френеля для функции частотного спектра первоначального импульса [2]. Представленный в данной работе метод и полученные результаты справедливы для импульсов, длительностью не меньше двадцати периодов.

Основные уравнения

В данной работе рассматривается распространение импульса в вакууме. Использовалась следующая нормировка: скорость света c и период несущего колебания T ₀ приравнивались к единице. Все временные переменные выражались через количество периодов, а пространственные переменные через количество длин волн несущего колебания.

Зададим поле во входной плоскости в виде E ( x , y , z = 0, t ) = p ( x , y )y( t ) . Эволюция пространственно-временной структуры поля импульса в скалярном приближении при распространении в вакууме описывается уравнением [1, 3, 4]

7 - I to          f. z      )

E ( x , y , z , t ) = j----- g ( ю ) exp l iC— i C t lx

0 2 n cz        X   c      )

от от             f r c x j j p(u, v)expl 5 i----(u - x)2 +

-от-от            X ^{L 2} cz

+ ( v - У ) 2 } dudvd c

где ю ₀ = 2 п - несущая частота; p ₀ = л) 2 для обеспечения условия y ( + T ) = 0; 2T - длительность импульса.

Частотный спектр импульса (2)

g ^{( ю} ) = ^{1 [ ex}P ⁽ i P 0 ) ~ ^{( ю , ю} 0 ⁾⁺               (3)

+ ^exp ^(- i P 0 ) ~ ^{( ю , - ю} 0 ^)]

где х 1 Sin (ю - ю0 )t

g ( c , ю 0 )=-------—               (4)

п to - Ю ₀

Функция (3) удовлетворяет условию для частотного спектра реальных импульсов g ( - с ) = g * ( ю ) [3].

Для упрощения дальнейших выкладок проанализируем функцию (3) и способ ее использования в (1). Первое слагаемое в (3) существенно отлично от нуля при положительных значениях ю ( ю ₀ >  0), в то время как второе при отрицательных ю . При выполнении условия

j| g(ю,®0)|2de

'----------------- << 1

от j| ~(ю,®0 )|2 de

и учитывая, что интегрирование в (1) ведется только по ю >  0 , предлагается второе слагаемое в (3) приравнять к нулю. Условие (5) выполняется для T >  10. С учетом всего вышесказанного, рассмотрим временную зависимость первоначального импульса в виде

1 ”

где g(ю) =—j у(t) exp(ict)dt - частотный спектр 2п -от входного импульса. При этом не накладывается никаких ограничений на исходное пространственновременное распределение поля.

Рассмотрим импульс с ярко выраженными передним и задним фронтами

~ ⁽ t ) =

exp ( i p 0 - i C 0 1 ) ;

0;

t | <  T t\ > T

(2а)

/(t ) =

Cos ^p P 0 - ® 0 t ); | t | <  T

0;

1 t | >  ^T

Частотный спектр (2а) равен (4).

Т.к. ~ ( ю , ю ₀ ) в области отрицательных частот принимает значения мало отличные от нуля, то нижний предел интегрирования в (1) можно положить равным минус бесконечности. Подставляя (4) в (1) и интегрируя по d e , получаем интегральное представление для поля импульса

где

E ( x , y , z , t ) =-----exp ( i ф ₀ + i ® ₀ t ) x

2ncz to to xJ J ^(n + TMu,v)dudv -

-to-to

-—exp ( i ф ₀ - i ® ₀ t ) x                       (6)

2ncz toto xj JYn -TY(u,vdudv —

-to -to

- ® " JJ ~ ⁽ П 1 M u , v ) dudv

^{2 n cz} G ( U , v )

E ( x , y , z , t ) = - iA ⁰ ® ⁰ x

2 zc

f x expl iф0 - i®0n

I

x

^P I P ² It Y Г Р Yz 2

J exp l ^-2Y Ы ² -у | d p ²

^J 2 V a ² J v c ² J

(7.3)

z   ( u - x ) ²    ( v - y ) ²

c 2 cz      2 cz

Первое и второе слагаемое в (6) описывают поле, создаваемое передним и задним фронтами первоначального импульса соответственно. При выполнении условия Im ( ^ ( u , v )) = 0, т.е. для начального импульса с плоским волновым фронтом, учитывая, что Re [ ~ ( ± T ) ] = 0, вклад первого и второго слагаемого в поле равен нулю. На область интегриро-

где p1 = 72 zc (n + T) - радиус окружности во входной плоскости с центром в точке (u = x, v = y), с которой начальное поле уже влияет на поле в точке наблюдения (x, y, z, t);

P 2 = 4 ² zc ( n - T ) - радиус окружности во входной плоскости, с которой начальное поле уже не влияет на поле в точке наблюдения;

П = t - z - "бегущее время";

c

1 ₀ ( ... ) - модифицированная функция Бесселя [5];

вания третьего слагаемого наложены ограничения из условия |т | <  T , возникающего при задании временного профиля первоначального импульса (2а).

Из полученного интегрального представления поля следует, что временная структура импульса влияет на эволюцию пространственно-временного распределения поля при его распространении.

Рассмотрим импульс с гауссовским распреде-

r = V x ² + y ²

11 i ® ₀

= . a ² ( z ) c ²    2 zc

Формулы (7) дают окончательное выражение поля импульса вида (2а) при z > 0 для любого мо-

мента времени.

В случае c ^ to (что соответствует бесконечному в поперечном сечении импульсу) из (7) получаем

лением

^ ( u , v ) = exp l

в поперечном

u ² + v ²

c

. Из (6) получаем

сечении следую-

lim E ⁽ x , y , z , t ) = A 0 / ⁽ П ) c ^to

щие выражения для поля:

П < - T

- т.е. импульс распространяется без изменения.

При p ₁ ^to , т.е. когда поле в исследуемой точке формируется всем первоначальным импульсом, получаем обычный гауссов пучок в параболическом приближении [1], что и следовало ожидать

E ( x , y , z , t ) ^ 0 - поле не дошло

E_c ( x , y , z , t ) =

до этой точки

IП <  T

(7.1)

c p2 (z)

f exp

V

r ²

P^(z) J

~ (n)

где p ( z ) = c 1 + i — z— ]    ^K 0 ^c

E ( x , y , z , t ) = - A®- x

2 zc

f x expl iф0 - i®0n2 | x

I

Поле на оси определяется выражениями

|n| < T

(7.2)

E ( x , y , z , t ) = - iA 0 ® 0- a ² ( z ) x

2 zc

x

^p f

J exp

0 v

^p li e ^f 2 ^P | d p ² a J V c J

x exp ( i ^ ₀ - i ® ₀ n ) 1 -

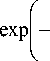
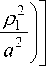
(9.1)

П > T

П >  T

E ( x , У , z , t ) = - A ^ ⁰- a 2 ( z ) x

2 zc

x exp ( i p ₀ - i ro ₀ n ) exp l

-

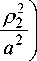
(9.2)

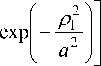
Время нарастания амплитуды поля на оси ( и время спада ) равно

. ст ^г

Nn «---

2 zc

Видно, что длительность процесса установления и спада амплитуды поля обратно пропорционально расстоянию до входной плоскости. Элементарные оценки показывают, что эти процессы могут занимать от нескольких периодов до долей периода.

Перед обсуждением результатов моделирования следует сделать замечание о величинах, которые следует рассматривать в нашем случае.

При стандартном рассмотрении поля в скалярном приближении его задают в виде E = A exp ( i p ) .

Плотность энергии электромагнитного поля Q [6], величина, регистрируемая приборами, определяется уравнением

1 c ²

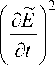
+ ^{( v} E ) ²

~      \ _ 8   8

где E = Re(E), V = —+--- для полей с цилиндри-' '       8z 8 r ческой симметрией. Получаем, что

E _t = A t Cos ( p ) + A p t Cos ( p + n /2 )        (12.1)

E _z = A z Cos ( p ) + A p z Cos pp + n /2 )      (12.2)

E _r = A r Cos ( p ) + A p r Cos ( р + n /2 )       (12.3)

где p ~ rot - k z . Учитывая малость длин волн для электромагнитного спектра, первыми слагаемыми в первых двух уравнениях пренебрегают по сравнению со вторым, что эквивалентно применению метода медленно меняющихся амплитуд.

Значение слагаемых третьего уравнения так же малы по сравнению с оставленными членами. Учитывая, что среднее значение Cos ² ( р + П 2 ) за период равно 0.5, получаем - плотность энергии электромагнитного поля для длинных импульсов про- 2 порциональна A ² или E .

В случае же переходных процессов метод медленно меняющихся амплитуд не применим. Для данных процессов следует рассматривать I Re ( E ) , т.е. действительное значение поля.

При помощи полученных уравнений (7) исследуем эволюцию пространственно-временной структуры импульса со следующими параметрами: T = 10, a ₀ = 10 ³ .

На рисунках 1-3 представлены распределение действительной части и амплитуды поля рассчитанного по формуле (7) для различных расстояний от входной плоскости. Видно, что в пространственновременном распределении амплитуды поля наблюдаются ярко выраженные процессы установления и спада, их длительность оценивается формулой (10). На переднем фронте наблюдается всплеск амплитуды, который уменьшается по мере удаления от входной плоскости. В ходе выхода амплитуды поля на стационарное значение, она претерпевает осцилляции с частотой го ₀ . На периферии пучка переходные процессы начинаются позже и длятся дольше, чем на оси. В пространственно-временном распределении I Re ( E )| не наблюдается сколь либо заметных переходных процессов. Можно сделать вывод, что для физически наблюдаемых параметров электромагнитного импульса процесс установления и спада происходит мгновенно.

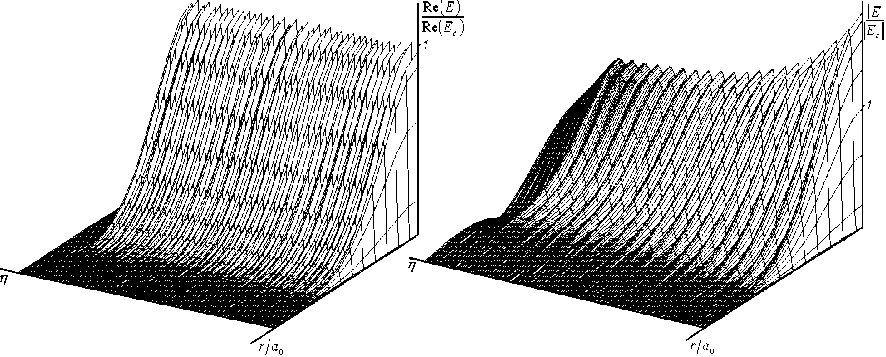
Рис.1. Радиальное распределение | Re( E ) | и | E | для импульса (2а) на расстояние z = 100 ■ a ₀ .

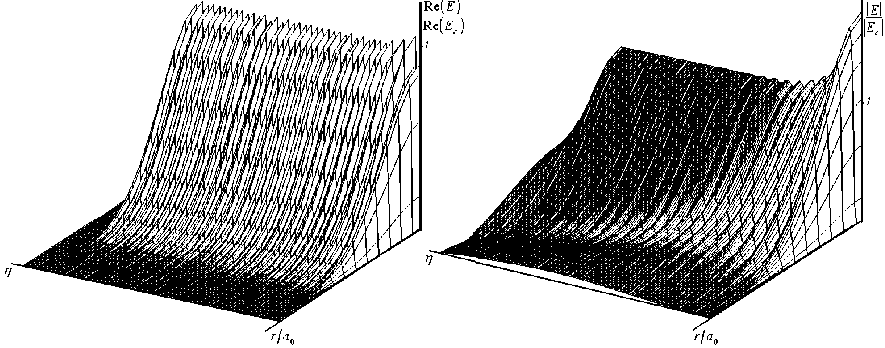
Рис.2. Радиальное распределение Re( E )

и | E | для импульса (2а) на расстояние z = 300 ■ a ₀ .

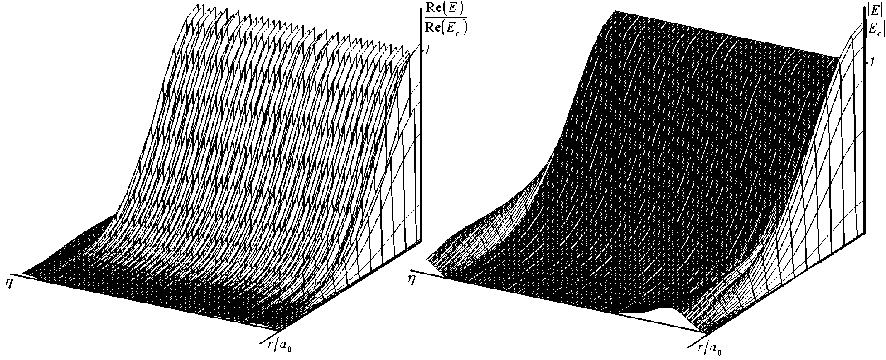
Рис.3. Радиальное распределение | Re( E )| и |Е| для импульса (2а) на расстояние z = 1500 ■ a ₀

Вывод

Специальным подбором функции временного профиля с крутым фронтом удалось получить удобное интегральное представление для поля импульса с гауссовым распределением в поперечном сечении. Показано, что для поля импульсов, длительностью более двадцати периодов, отсутствуют ярко выраженные переходные процессы (амплитуда переходных процессов пренебрежимо мала по сравнению с абсолютным значением |Re(E)|).

Результаты, представленные в данной статье, являются справедливыми для любых волновых процессов описываемых волновым уравнением.