Исследование рабочих процессов в рекуператоре энергетической микрогазотурбинной установки

Газовоздушный рекуператор энергетической микрогазотурбинной установки (МГТУ) предназначен для повышения коэффициента полезного действия (КПД) установки за счёт дополнительного подогрева воздуха, выходящего из компрессора. Нагрев воздуха в рекуператоре происходит за счёт тепла выхлопных газов (продуктов сгорания), выходящих из турбины. На рис. 1 представлен цикл МГТУс регенерацией теплоты и сгоранием топлива при постоянном давлении.

Рис. 1. Схема цикла МГТУ

Исходное состояние воздуха на входе в компрессор определяется точкой 1. Сжатый воздух после компрессора (точка 2) подогревается в рекуператоре за счёт теплоты продуктов сгорания (процесс 2–5) и подаётся в камеру сгорания. Таким образом, часть отводимой теплоты возвращается в цикл. Точки 7 и 8 соответствуют полной регенерации, точки 5 и 6 соответствуют частичной регенерации. Полнота регенерации характеризуется степенью регенерации

При заданных степени регенерации и температуры Т4 после турбины из (1) можно найти температуру воздуха после рекуператора

T5 = T2 +°(T4 - T2 ) .

Оба теплоносителя в рекуператоре МГТУ – газы, расходы которых отличаются незначительно. Так как коэффициенты теплоотдачи к газам невелики, для передачи тепла требуется развитая поверхность теплообмена (значительно большая, чем в теплообменниках, реализующих схемы

«жидкость – жидкость» или «жидкость – газ».

Рассматривается кольцевой рекуператор пластинчатого типа, схема которого представлена на рис. 2. Схема пластин рекуператора представлена на рис. 3.

Рис. 2. Принципиальная конструктивная схема кольцевого противоточного пластинчатого рекуператора (стрелками показано движение горячих газов и воздуха)

Кириллов В.В., Карташев А.Л.

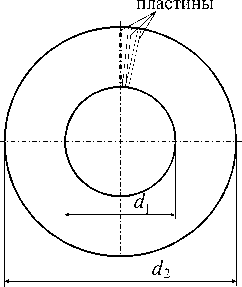
Рис. 3. Схема пластин рекуператора

пластина

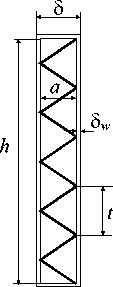
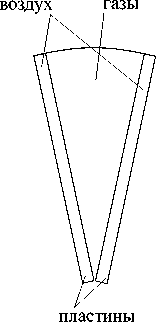
Пластины располагаются внутри цилиндрического корпуса. Воздух движется внутри прямоугольных пластин, продукты сгорания в режиме противотока движутся между пластинами. Количество пластин теплообменника определяется по формуле

N — ^,

где d 1 - внутренний диаметр, 5 - толщина пластины (см. рис. 3).

Для увеличения тепловых потоков в таких теплообменниках широко применяется оребрение поверхности теплообмена. С этой целью внутри воздушной пластины устанавливается гофрированная вставка (воздух движется в каналах треугольной формы).

Количество тепла, передаваемое воздуху, определяется по уравнению баланса тепла

Q = G в С р в ( T ₅ - T 2 ) = G _г С р _г ( T 4 - Т б ) ,                                                            (4)

где G – расход, c p – удельная теплоёмкость; T – температура; индексы: в – воздух; г – продукты сгорания (далее, газы). Теплоёмкости воздуха и газов рассчитываются по средним температурам.

Высота пластины h при заданной толщине 5 определяется следующим образом. Находят площадь сечения прохода газов Sг , предварительно задав их скорость wг

S г

G г

Р г ^ г

С другой стороны

пГ(dj + 2h)2 - d21

S = ^----------- ^ - Nh 5 = п h ².

г 4

Отсюда h=SF ■ п

Скорость воздуха в пластине находится по формуле

N Р в a ( h - 2 5 _w )"

Изменение температуры воздуха и газов по длине теплообменника можно определить из решения уравнений энергии dTв KвПв (Тг - Тв )

---- — ----------------- ;                                                                                    (8)

dx       Gвcpв dT = KгПг (Тг - Тв) dx       Gгcpг

здесь П – обогреваемый периметр; K – коэффициенты теплопередачи.

Краткие сообщения в Fb ^F + 1  ; г X "w + 1 Fl аН г '^w 2 г априв аг ^W априв 1 в

Коэффициенты, входящие в (10), приведены в работах [1, 2]

F_p /      \        th ( ml р/2 )

^а прив = ^а в ^П 0в ; ^П 0в = ¹ ^\1 - ^П р ) ; ^П р =      7 /о ; m =

F _в                 ml _р 2

^{2 а} в

N5pxp ’

здесь а - коэффициент теплоотдачи; F - площадь поверхности; lр - длина ребра; 5р - толщи на ребра; X - коэффициент теплопроводности; х - координата вдоль пластины; индексы: w -стенка, р – ребро.

Начальные условия для уравнений (8) и (9) задаются в виде

T b ( 0 ) = Т 2 ; Т ( 0 ) = Т б .                                                                        (11)

Коэффициенты теплоотдачи рассчитываются по критериальным уравнениям в зависимости от режима течения. В числах Рейнольдса в качестве характерного размера используются эквивалентные диаметры d _э = 4 8/ П. При течении в щелевых каналах при ламинарном режиме число Нуссельта рекомендуется принимать равным 7,55 [3]. При турбулентном режиме течения можно использовать уравнение Михеева [1, 4]: Nu = 0,021Re^0,8 Pr^0,43.

Изменение давления по длине теплообменника рассчитывается по уравнениям импульса для воздуха и газов

— f -G2L- ₊         5 ^П^в -

dx ISвРв pbb)    '' 8Sb2Pb • d Г G2 d s G2П

+ Pг Sг = г г , dx ( Sг Рг       J     8 Sг2рг здесь S - площадь сечения; p - давление; ^ - коэффициент гидравлического сопротивления; р - плотность.

Начальные условия для уравнений (12) и (13) записываются в виде: p _в ( 0 ) = p ₂; p _г ( L ) = p ₄.

Уравнения (8), (9), (12), (13) решались численно методом Рунге-Кутта 4-го порядка. Интегрирование ведётся до тех пор, пока температуры воздуха и газов не станут равными T ₅ и T ₄ , соответственно. При этом за длину пластины принимается значение координаты х .

В таблице представлены результаты расчёта противоточного рекуператора с оребрённой воздушной пластиной, шаг оребрения t = 3 мм, толщина 5 _р = 0,12 мм. Газовый канал без рёбер. Количество пластин - 523, высота пластины h = 0,19 м, толщина пластины 5 = 2,4 мм, толщина стенки 5 _w = 0,2 мм, диаметр d 1 = 0,4 м. Температуры: Т ₂ = 248,2 °С, Т ₄ = 603 °С. Давления: p ₂ = 0,55 МПа, p ₄ ® 0,1 МПа. Расходы воздуха и газов равны G _в = 1,04 кг/с и G _г = 1,05 кг/с.

Результаты расчёта рекуператора с оребрённой воздушной пластиной

ст	K в , Вт/м2К	_ K _г , Вт/м2К	L , м	A p в , кПа	A p г,кПа	F в , м2	F г , м2	2k Т , °C	Т 5 , °C	Т 6 , °C
0,6	27,7	73,6	0,117	0,698	0,48	61,6	23,3	159,6	461,1	403,9
0,7	27,5	73,1	0,180	1,15	0,74	95,3	35,9	123,6	496,6	370
0,8	27,3	72,4	0,306	2,06	1,25	161,8	60,96	87,3	532,0	336,0
0,9	21,2	72,3	0,676	4,87	2,79	357,1	134,5	49,3	567,5	301,5

Представленная математическая модель и метод расчета позволили провести исследование рабочих процессов в рекуператоре МГТУ, реализующем регенерацию тепловой энергии продуктов сгорания с целью повышения КПД установки. Приведены результаты математического моделирования рабочих процессов в кольцевом рекуператоре пластинчатого типа.