Исследование реального трафика в телекоммуникационных и компьютерных сетях

Как известно, в сетях NGN отсутствуют выделенные канальные ресурсы для передачи сигнального трафика. Последний в составе трафика протокола SIP обслуживается на основе общих транспортных механизмов, и в этом случае важным является вопрос исследования вероятностновременных характеристик трафика SIP-серверов. Сам же протокол SIP может использовать различные протоколы транспортного уровня, а для передачи голоса и видео в рамках организованного средствами SIP сеанса связи обычно используется протокол RTP. SIP-устройства для передачи звука и видео используют различные алгоритмы сжатия и кодирования данных (кодеки). Известно, что используемые для кодирования речи кодеки (G.711, G.723.1, G.729 и др.) порождают трафик, обладающий свойствами самоподобного случайного процесса [1]. Следовательно, такими же свойствами должен обладать и агрегированный трафик, обрабатываемый SIP-серверами, в чем мы и хотим убедиться.

Съем и анализ трафика

Были произведены измерения сигнального и агрегированного трафиков (числа пакетов в минуту) абонентов услуги IP-телефонии одного из самарских операторов по схеме, приведенной на рис. 1, а также пользователей внутренней сети вуза (университетский трафик) с помощью программы Netflow Analizer.

Из полученных трасс были выделены периоды активности пользователей, примерно с 8.30 до 20.30 местного времени. Сигнальный трафик одного такого периода активности представлен на рис. 2. Для него среднее значение равно 20,46; дисперсия – 3,6; коэффициент вариации – 0,04.

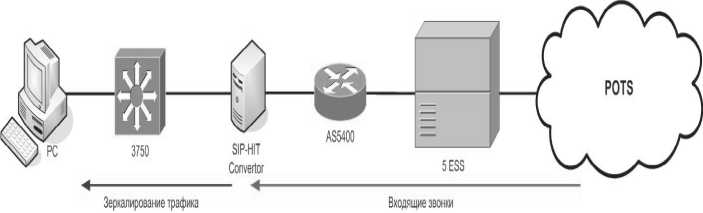
Рис. 1. Схема фиксации трафика IP-телефонии

Ввиду достаточной ровности почти регулярного сигнального трафика и его малой величины из рассмотрения его можно исключить. Для агрегированного SIP-трафика (см. рис. 3) среднее значение в пакетах 693,45; дисперсия – 155642,36; коэффициент вариации – 0,57.

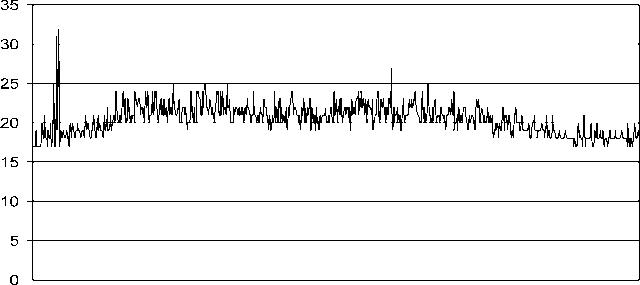
Рис. 2. Реализация сигнального трафика

Для трафика сети кафедры вуза (см. рис. 4) среднее значение 23,2; дисперсия – 595,36; коэффициент вариации – 1,05; а для сети двух факультетов вуза (см. рис. 5) среднее значение 191,67; дисперсия – 33502; коэффициент вариации – 0,955.

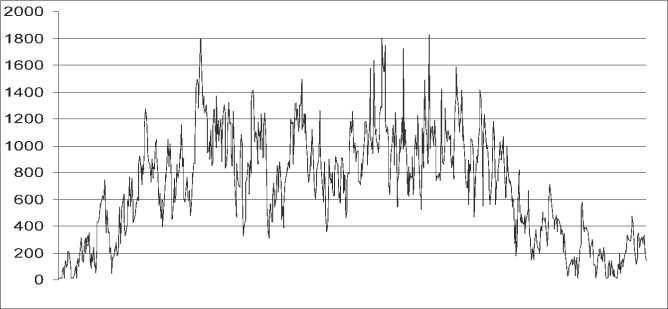
Рис. 3. Реализация агрегированного трафика

Учитывая, что для пуассоновского потока математическое ожидание и дисперсия случайного числа пакетов трафика должны совпадать, в нашем случае мы имеем, что все три вида трафика представляют собой далеко не пуассоновские потоки.

n

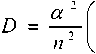
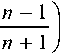
m

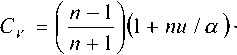
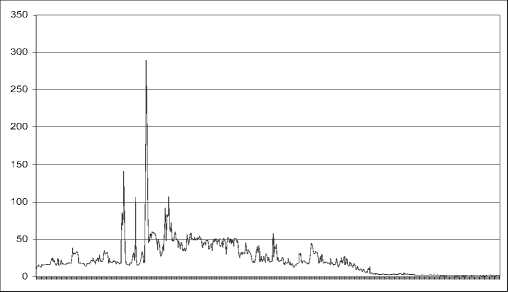
Рис. 4. Реализация трафика локальной сети кафедры

Отсюда следует важный вывод о том, что реальные трафики отличаются от пуассоновских потоков. Следовательно, для их анализа применение классических моделей массового обслуживания неправомерно, так как они занижают вероятностно-временные показатели функционирования системы (см. таблицы 1-3).

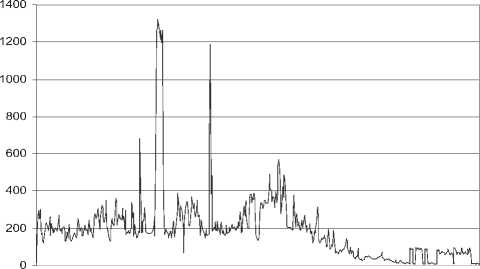
Рис. 5. Реализация трафика локальной сети вуза

Анализ вида распределений данных трасс показал, что для всех трех трафиков с наибольшей вероятностью в качестве модели подходит распределение Wakeby [6]. Это распределение используется, например, в гидрологии для исследования паводковых явлений:

F(x) = 1 - fl - -——) ■        (1)

V a )

Числовые характеристики (1) представляют собой

□ Histogram-Wakeby |

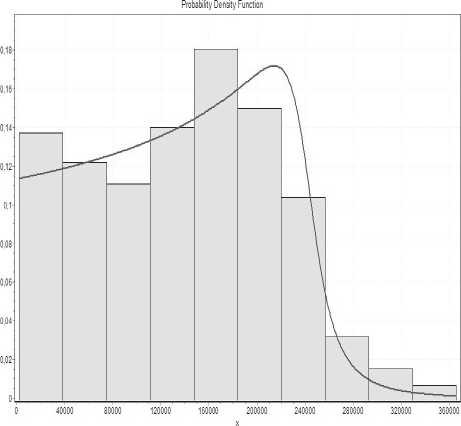
Рис. 6. Аппроксимация гистограммы распределением Wakeby

Для агрегированного SIP-трафика параметры этого распределения n = 8,197; u = 2,214; α = 4876,102. Вид распределения Wakeby применительно к SIP-трафику показан на рис. 6. Оно имеет среднее значение m = 611,7 и дисперсию D = 275014. Для трафика сети кафедры параметры распределения Wakeby: n = 0,132; u = 31,381; α = –0,756; а числовые характеристики равны m = =25,65; D = 456,4. Аналогично для сети двух факультетов: n = 1,62 • 10^-4; u = 0,023; α = 0,035; m = 218,45; D = 47708.

Сравнение числовых характеристик распределения Wakeby для всех трех типов трафика с их найденными выше моментными характеристиками показывает, что это распределение вполне подходит в качестве модели для исследования трафика. Для перехода от случайного потока к анализу интервалов времени между событиями в потоке были использованы приближенные соотношения из [3], которые позволяют оценить распределение интервалов времени на уровне двух первых моментов. Для этого обозначим N ( t ) – число событий (количество пакетов) за в ремя t .

Тогда среднее N ( t ): N = t / т , где т – среднее время между событиями в потоке N ( t ). Тогда дисперсия числа событий N ( t ) D_N=D_T.t/r выражается через среднее значение и дисперсию интервала времени между событиями [2].

Для сигнального трафика оценка математического ожидания составила 2,928 С, дисперсии – 0,00212; коэффициент вариации – 0,0156. Таким образом, мы снова убеждаемся в том, что сигнальный трафик является почти регулярным, и, как было отмечено выше, его далее можно не рассматривать.

Преобразование входного трафика применительно к системе массового обслуживания (СМО)

В связи с тем, что процессы поступления N ₁ и обслуживания N ₂ в СМО являются ступенчатыми вероятностными процессами с единичными приращениями в случайные моменты времени поступления пакетов (см. рис. 7) [2], исходный трафик, представляющий собой совокупность случайных отсчетов (количества пакетов) за минутные промежутки времени, должен быть соответствующим образом преобразован. Для этого на каждом промежутке времени длиной в одну минуту случайным образом генерируем количество интервалов, равное количеству пакетов за эту минуту, с использованием генератора СЧ random. После этого исходный трафик и преобразуется к ступенчатому процессу поступления.

N/Of

время

Рис. 7. Реализация процессов поступления и обслу- живания

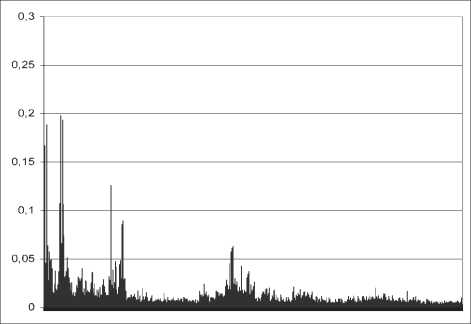
Рис. 8. К расчету коэффициента Херста

Результат такого преобразования для агрегированного SIP-трафика представлен на рис. 8. Для подбора типа СМО исследуем числовые характеристики распределения интервалов времени между пакетами преобразованных трафиков. В результате получили следующие статистические характеристики для агрегированного трафика: среднее значение – 0,0864; дисперсия – 0,0432; коэффициент вариации – 2,41. Для сети кафедры среднее значение – 2,4384; дисперсия – 0,3618; коэффициент вариации – 1,91. Для университетско-го-2 трафика среднее значение – 0,3126; дисперсия – 21,708; коэффициент вариации – 2,12. Таким образом, анализ вида распределений интервалов времени между пакетами показывает, что все они в данном случае имеют «тяжелые хвосты». Распознавание закона распределения интервалов времени между пакетами в трафике и проверка гипотезы о виде распределения не всегда могут дать конкретный результат с высокой вероятностью.

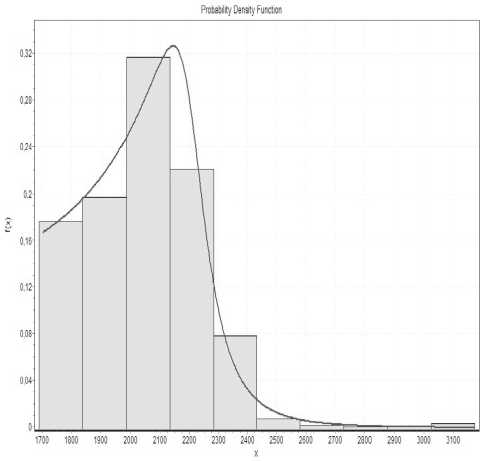
□ Histogram-Wakeby |

Рис. 9. Аппроксимация гистограммы распределением Wakeby для SIP-трафика

На рис. 9 показан результат распознавания закона распределения для интервалов времени между пакетами агрегированного SIP-трафика, в то же время для остальных двух трафиков подобрать распределение с достаточной вероятностью не удалось. Тем не менее, в данном случае мы располагаем достаточными сведениями о характере распределения рассматриваемых трафиков (среднее значение, дисперсия и коэффициент вариации). Кроме того, результаты [5] позволяют анализировать имеющиеся трафики на самоподо- бие. Для этого определим значения коэффициента Херста H.

Коэффициент Херста для агрегированного SIP-трафика составляет Н = 0,89 (см. рис. 10). Для университетских трафиков коэффициент Херста составил Н = 0,87 и Н = 0,89 соответственно. Следовательно, подтверждается гипотеза о том, что распределения с коэффициентами вариаций, большими 1, имеют показатель Херста выше 0,5.

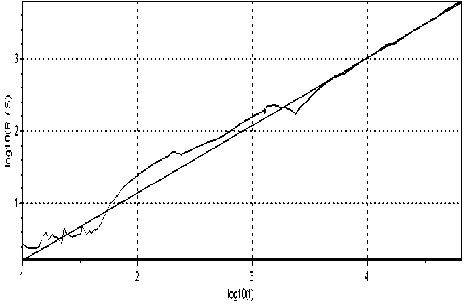
Рис. 10. К расчету коэффициента Херста для SIP-трафика

Результаты анализа приведенного SIP-трафика позволяют представить модель передачи данных между SIP-устройствами по IP-сети в виде соединения однолинейных СМО с неограниченным буфером типа G/D/1.

Таблица 1. Система G/D/1, Сv = 2,41

р	иш.	Результаты дифф. аппр.	Результаты M/D/1
0,1	1,223	1,167	1,056
0,3	2,211	2,122	1,214
0,5	3,789	3,646	1,50
0,7	7,021	6,498	2,167
0,9	21,434	19,95	5,5

Таблица 2. Система G/M/1, Сv = 1,91

Р	и»,	Результаты дифф. аппр.	Результаты М/М/1
0,1	1,420	1,275	1,111
0,3	2,138	2,099	1,429
0,5	3,574	3,473	2,0
0,7	6,729	6,381	3,333
0,9	21,578	20,36	10,0

Таблица 3. Система G/M/1, Сv = 2,12

Р	U им	Результаты дифф. аппр.	Результаты М/М/1
0,1	1,423	1,341	1,111
0,3	2,438	2,341	1,429
0,5	3,992	3,963	2,0
0,7	7,775	7,359	3,333
0,9	24,553	23,53	10,0

При помощи программы, описанной в [4], получим результаты, приведенные в таблицах 1-3. Здесь приведены расчетные данные для средней задержки (время ожидания плюс время обслуживания), причем среднее время обслуживания для удобства взято нормированным, то есть равно единице. Для сравнения в таблицах 1-3 приведены также результаты двумерного диффузионного приближения СМО [3] и классических СМО M/D/1 и M/M/1. Их сравнение показывает достаточную близость результатов двух разных подходов: метода Монте-Карло и метода двумерной диффузионной аппроксимации СМО для расчета характеристик СМО G/G/1/.

Выводы

Предложен подход к анализу трафика сети методами СМО, который требует соответствующего преобразования трафика для приведения его к ступенчатому процессу. Подтверждено, что реальные трафики отличаются от пуассоновских потоков и могут быть самоподобными. Сравнение полученных результатов с классическими моделями показывает, с одной стороны, их степень различия, а с другой – насколько классические модели могут занижать качественные и количественные показатели производительности системы. Следовательно, классические модели в случае самоподобного трафика показывают слишком оптимистичные результаты.