Исследование решений сингулярно возмущенных обыкновенных дифференциальных уравнений

Бюллетень науки и практики / Bulletin of Science and Practice Т. 9. №3. 2023

УДК 517.928                                      

В работе исследуется решения нелинейной задачи. Если неоднородная часть f ( t ) = 0 , то решению сингулярной задачи можно исследовать в действительной области. Собственные значения Жордановой матрицы определяют условия устойчивости. Например, если собственные значения состоит чисто мнимых частей, то действительная ось будет устойчивым. Соответственно исследования проводится по действительной оси. А также комплексно-сопряженные собственные значения определяют двухсторонняя устойчивая область, которая внутри этой области выполняется несколько раз смены условия устойчивости.

Цель исследования. Доказать асимптотическую близость решений сингулярно возмущенных обыкновенных дифференциальных уравнений и соответствующей невозмущенной уравнений, в случае смены устойчивости.

Материалы и методы исследования

Рассматривается    следующие    сингулярно    возмущенные    обыкновенные дифференциальные уравнения:

£ x ' ( t , £ ) = J ( t ) X ( t , £ ) + £ f ( t , X ( t , £ ))

X(10, £) = X° ||x0 11 = const где 0 < £ - малый параметр, t g [t0, T] , f (t, x(t, £)) = colon(f (t,x),..., f6 (t, x)) , x0 - const , J(t) = diag(J1(A1(t)),.J2(A2(t))), где

' A( t) 0 0 > f A( t) 0 0  > , x (t, £) — искомая неизвестная J 1(M t)) = 1 ACt) 0 , J 2(M t)) = 1 ^2 (t) 0 k 0 1 A( t) j k 0 1 A( t) j функция.

Для решения поставленной задачи от правых частей (1) потребуем выполнения следующих условий:

~          x        x

U1.  f (t,0) = 0 , f (t,x) - f (t,x) < M x x - x max|x||,||x|} ,  0 < M — некоторая постоянная, не зависящая от £ .

U2. Re A ( t ) <  0 , 1 ₀ <  t <  T₀ ; Re A ( T ) = 0; Re A ( t ) >  0 , T₀ <  t <  T , k = 12.

Определим область

Q = |(t, x)| t g [t0, T], |x| < a, k = 1, n}, где 0 < a - некоторая постоянная, не зависящая от £ .

Имеет место следующая теорема:

Теорема. Пусть выполнены условия U1-U2. Тогда V t g [ t ₀, T ] решение задачи (1)-(2)

существует, единственно и для него справедлива оценка

||x ( t , £ )|| <  C 3 ( £ ) ,                                                      (3)

где £ = o(5(£ )) , C - const .

Доказательство. Задачу (1)-(2) заменим следующим эквивалентным интегральным уравнением

t

k

t

t

t                           t              I t                   '

x ( t , £ ) = x ⁰ exp — j J ( s ) ds + j exp — J J ( s ) ds I f ( t , x ( t , £ )) d T

I ^£'         J   t ^J0     I ^£ T        J

k

t 0

)

t 0

Для доказательства существования решения уравнения (4) применим метод последовательных приближений.

Последовательные приближения определим следующим образом:

x 0 ( t , £ ) = 0 ,

t

k

t

t

k

^x m ⁽ t , ^£ ) =

x ^oexp ^j J ( s ) ds + jexp ^j J ( s ) ds f ( t , x m - 1 ( т , £ )) d T I ^£ t 0         )        k ^£ T        )

k

t 0

J

где x _m ( t , £ ) = colon ( x i m ( t , £ ), x 2 _m ( t , £ ),..., x 6 _m ( t , £ )) , m = 1,2,... .

Учитывая U1, первое приближения будет x j ( t , £ ) = x ⁰

k

t

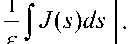
J k   t 0

Справедлива оценка

~

II x 1 ⁽ t , ^s )|| <  C W)

Малая величина конкретизируется завися от порядкой нули собственных значений

Жордановой матрицы.

~       ~     2

Оценим второе приближения x ₂ ( t , s ) <  C 8 ( s ) + ( C 8 ( s ) ) .

Для m -го приближения справедлива оценка

~       ~            /~            ~ xm (t, s) < C8(s) + (C8(s)) +... + (C^(s)) , где C — некоторая постоянная, m g N .

Действительно, это можно доказать, применяя метод математической индукции. При m = 1 мы уже доказали верность. Пусть т = k :

||x_k (t , s )|| <  C S ( s ) + ( C S ( s ))² + ... + ( C S ( s )) ^k .

Для ( k + 1 ) го приближения имеем:

II X k + 1 ( t , s )|| <  C 8 ( s ) + ( C 8 ( s ))² + ... + ( C 8 ( s )) ^{k + 1}.

Последовательные приближения равномерно ограничены, действительно,

~ vm e N: ||xm (t, £)|| < C8(£) .

Рассмотрим ряд

||^Xm ⁽ t , ^£ )|| = || ^X 1 ⁽ t , ^£ ОЦ ^{+ (}| ^X 2 ⁽ t , ^£ OH - || ^X 1 ⁽ t , ^£ 0| |^{)+ (}| ^X 3 ⁽ t , ^£ 0|| - || ^X 2 ⁽ t , ^{£ )}||⁾⁺ ... ^{+ (}| ^Xm ⁽ t , ^£ )|| - || ^Xm - 1 ⁽ t , ^£ 0||)

Так как

||X 1 ( t , £ )|| <  C< 5 ( s ) <  1 ,

||^X 2 ⁽ t , ^s ' ⁾||^-1| ^X 1 ⁽ t , ^s ОЦ <  C W^{)) 2}<  ¹ ,

||^X 3 ⁽ t , ^£ 0|| -I | ^X 2 ⁽ t , ^£ 0|| <  ( C W⁾⁾³ <  ¹ ,

II Xm (t , £0|| -||Xm-1( t , s0|| <(CW ))m 1 < 1 , то в рассматриваемой области последовательность {Xm (t, s)} является сходящимся и имеет предел x(t, s):

~

||^Xm ⁽ t , ^s °| <  ^C ^ ^{( s} ) ^X

Г

k

( ~     \m +1 Л

Jc^L

1 - C 8 ( s )    I

~ и при m ^® получим ||x(t, s)|| < C8(s).

Теорема доказана.

Определение. Если решения задачи (1)-(2) существует в - 1 ₀ <  t <  1 ₀ , ( 1 ₀ =+да не исключается) и ограничено, то это решение назовем двухсторонне устойчивым на [— 1 ₀, t ₀ ] .

Пример 1. Пусть собственные значения Жорданова матрица функция будет \ ( t ) = t ³ - 1 + i ( 2 1 ² - 1 )    ,     й ₂ ( t ) = t ² - 1 - i ( 2 1 ² - 1 )    . Действительная часть равна

Re \ ( t ) = Re ^ ( t ) = t ² - 1 . Действительная часть собственных значений определяет устойчивые и неустойчивые интервалы. Решаем, как уравнения имеем: ^ = - 1 , t₂ = 0 , t₃ = 1 . Re ^ ( t ) = Re ^ ( t ) <  0 при t e ( -да , - 1 ) о ( 0,1 ) , Re \ ( t ) = Re ^ ( t ) >  0 при t e ( - 1,0 ) о ( 1, +да ) , точка t = — 1 является точкой перехода от устойчивого к неустойчивым интервалам, а также точка t = 0 является точкой перехода от неустойчивой к устойчивому интервалу.

t

Найдем первообразную функцию   A;(t,t0) — j(s3 -s + i(2s2 - 1))ds   и также для t0

t

- s -

i ( 2 s ² - 1 )) ds . Находим действительную

сопряженных собственных значений A ₂ ( t , t ₀) = j (s³

t ₀

и мнимую часть Re A j ( t , t ₀) =

t ⁴ - 2 1² - (^ ⁴ - 2 1₀ ² )

, Re A ₂ ( t , £ ) =

t ⁴ - 2 1² - ( t 4⁴ - 2 1 2 )

,

( 2, I

Im A^ ( t , t^ ) — I — t - 1 I -

3 ^{t 0}

—

I                                I 2 ^2         I I 2 ^2

t I , Im A_? ( t , t ) — -I — t - 1 I +1 — t 0     20             0

—

t ₀

.

Действительную часть первообразную функцию решаем как уравнения. Тогда имеем Re A J t , 1 0 ) — Re A ₂( t , 1 0 ) — 0 или t ⁴ - 2 t ²- ( t 4⁴ - 2 t 22 ) — 0 , ( t ² - t ₀2 )( t ² + t ₀2 - 2 ) — 0 , имеем t ² - t ₀2 — 0 и t ² + 1 2 - 2 — 0 . Корни уравнения 1 1 — - 1 ₀ , 1 ₂ — 1 ₀ , 1 3 — -^2 - 1 2 , 1 ₄ — ^ 2 - 1 02 .

Выделим следующие случаи:

• 1) . Пусть t₀ — 0 . Тогда Re A ( t ,0) — Re A ₂ ( t ,0) <  0 при t e [ - 72,0 ] o [ 0,72 ] -устойчивый или регулярный интервал, Re A_{ ( t ,0) — Re A₂ ( t ,0) >  0 при t e ( -да , - 41 ) o ( 42,+A- неустойчивый или

• сингулярный интервал.

t e [- 72,0]o [0,72] интервал двухсторонне устойчиво, в каждой из этих интервалах собственные значения меняет условия устойчивости. Интервал t e[- 22,22] является двухсторонне приближений

устойчивый интервал. Уравнению (4), решаем методом последовательных xw(t, £) = 0

t

t

t

x 1 m ⁽ t , ^£ ) ^—

x ^oexp - рд s ) ds + jexp - j\( s ) ds f (t. V ^£           J 0 I ^£ T         J

V

J

, x m -1

( t , £ )) d r , m — 2,3,...

Оценим

I X -i ( t , £ )| <  C « i ( £ )

n t.

x 12 ⁽ t , ^£ ) <  x 11 ⁽ t , ^£ ) ⁺ J ^eXP “f ^{4 ( s} ) ^ds f ^{( t} £

t

t

\

t

t

V

t

J

, x ₁₁

x ₆₁

1 t-           1

) d r + — j exp — ^4 ( s ) ds £      £

V

t

J

x 21 ^{( r} , ^£ ) <

< 1 x 11 ⁽ t , ^£ ) ⁺ M 0

t       1 1

exp -Re

0    V ^£

t           I

J 4 ( s ) ds r        J

max { x 11 1,..., x 61 |} d

^{T + 1} l x 20 lj

^£     0

t

\

exp —Re J 4 ( s ) ds d r < V £   0         J

< I ^х 101 exp

t

V

1             t-

— Re j ^ ( s ) ds + M_o x⁰

£

J

t

1 J exp | £

V

j 4 ( s ) ds + j 4 ( s ) ds II d r +

V T             0           Jj

+ 1 x ’lJ ^£     0

exp

1Re

V ^£

t           I j 4 (s)ds dr < Ca, (£). Получим |xt2(t, £)| < Ca(£).

0        J

Собственные значения комплексно-сопряженные, поэтому аналогично получим оценку I x ₂₂( t , £ )| <  Ca(£ ) .

• 2) . Пусть t₀ — - 3 . В рассматриваемой области Re 4 ( t ) несколько раз меняет условия устойчивости. Оценку можно проводить в действительной области.

• 3) . Пусть t ₀ e ( - 72, - 1 ) и ( - 1,0 ) o ( 0,1 ) o ( 1,V2 ) . Тогда появиться две устойчивые области с затягиванием потеря устойчивости. Увеличить время задержки (потеря затягивания устойчивости) невозможно.

• 4) . Пусть t₀ = ± 1 . Тогда устойчивая область не существует, потому что появиться функция

  (t ir¹

  
  

всегда положительно.

Пример 2. Пусть \ ( t ) = t + i . За счет нелинейности, рассматриваемой уравнении можно увеличить затягивания потери устойчивости. Решения оценивается в действительной области.

Результаты и обсуждения. Выше рассматриваемый пример показывает, что если собственные значения удовлетворяет условию U 2, то они могут порождать двухсторонняя устойчивая область.

Двухсторонняя область состоит из двух частей. В каждой из них собственные значения сменить условия устойчивости.

Выводы

Если собственные значения Жордановой матрицы удовлетворяет условию U 2, то можно получить достаточно большое время задержки затягивания потери устойчивости. Это затягивание получается за счет нелинейности рассматриваемых уравнений.

Иногда собственные значения порождает двухсторонняя устойчивая область, которая раньше не рассматривалась.

Когда появиться двухсторонняя устойчивая область, тогда начальная точка дважды будет пограничной точкой, а ее окрестность дважды будет пограничным слоям.