Исследование резонансных магнитооптических свойств дифракционных структур, намагниченных в плоскости

Резонансные свойства металлодиэлектрических гетероструктур являются предметом интенсивных исследований [1]. Особый интерес представляют гетероструктуры, содержащие намагниченные материалы. Такие структуры наряду с резонансами пропускания и отражения могут обладать резонансными свойствами, связанными с преобразованием поляризации света.

В работах [2–6] исследовались магнитооптические свойства двухслойных гетероструктур, состоящих из дифракционной решётки и диэлектрического намагниченного слоя (вектор намагниченности перпендикулярен слою). В [2–6] показано, что такие структуры обладают как резонансами пропускания, так и резонансами углов Фарадея и Керра.

В работах [7, 8] рассмотрена двухслойная гетероструктура, содержащая металлическую дифракционную решётку и намагниченный слой. В отличие от [2–6], вектор намагниченности параллелен плоскости слоя и перпендикулярен штрихам решётки. В рамках численного моделирования в [7, 8] было показано, что в указанных структурах существует интенсивностный магнитооптический эффект, состоящий в резонансном изменении коэффициентов отражения и пропускания структуры при намагничивании слоя. В [7, 8] установлено, что условия возникновения магнитооптического эффекта совпадают с усло-

вием возбуждения TE- моды структуры. Однако, в [7, 8] не был подтвержден факт возбуждения моды, а представленные объяснения касались только уменьшения коэффициента пропускания, происходящего при намагничивании слоя. В [7, 8] также не рассматривались эффекты, связанные с преобразованием поляризации прошедшего света.

В данной работе показано, что интенсивнос-тный эффект носит более общий характер: перераспределение энергии между отражённой и прошедшей волнами может происходить произвольным образом и зависит от параметров структуры. В работе проведен анализ свойств структуры, обусловленных ее симметрией. В рамках численного моделирования впервые показано, что в подобных структурах наряду с эффектом резонансного изменения пропускания и отражения существуют резонансные эффекты, связанные с вращением плоскости поляризации.

1. ИНТЕНСИВНОСТНЫЙ

МАГНИТООПТИЧЕСКИЙ ЭФФЕКТ

Исследуемая структура состоит из металлической бинарной дифракционной решётки и намагниченного слоя (рис. 1). Вектор намагниченности слоя лежит в плоскости слоя и перпендикулярен штрихам решётки.

При указанном направлении намагниченности, тензор диэлектрической проницаемости материала слоя имеет вид [9, 10]

£   0

£M

ig

0   - ig

£

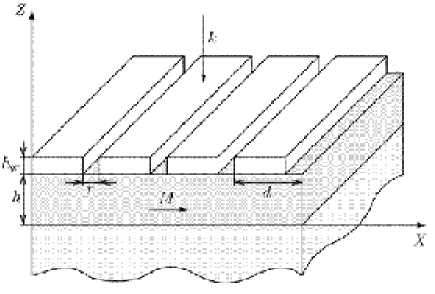
Рис. 1. Геометрия двухслойной структуры, содержащей дифракционную решётку и диэлектрический слой, намагниченный в плоскости где g — модуль вектора гирации среды, пропорциональный намагниченности. Магнитная проницаемость в видимом и ближнем ИК-диапазо-не считается равной единице [10].

Результаты численного исследования структуры на рис. 1 показывают, что при определённом сочетании геометрических параметров пропускание и отражение структуры сильно зависят от величины g [7, 8]. Структура предполагается субволновой, при этом под пропусканием и отражением понимаются интенсивности нулевых прошедших и отражённых порядков дифракции. На рис. 2 представлены расчётные спектры пропускания и отражения для намагниченного слоя и при отсутствии намагниченности. Расчёт спектров проводился по методу Фурье-мод [11, 12] для случая нормально падающей волны с ТМ-поляризацией. Расчёт проводился при следующих параметрах структуры: период решётки d = 552 нм , ширина отверстия r = 55 нм , толщина решётки hgr = 362 нм, толщина магнитного слоя h = 1935 нм. Для тензора диэлектрической проницаемости магнитного слоя (1) использовались параметры материала висмут-замещённый диспрозиевый феррит-гра-нат. В частности, при X = 1200нм, е=5.06+0.0004/, g = (1.53 - 0.003/)х10-2. В качестве значений диэлектрической проницаемости материала решётки использовались справочные данные для золота [13]. Диэлектрические проницаемости среды над структурой и материала подложки полагались равными 1 и 2.1, соответственно.

Рис. 2 показывает, что при намагниченном слое в спектре пропускания структуры появляется резкий минимум при длине волны X = 1200 нм . В спектре отражения на той же длине волны появляется симметричный максимум.

Под величиной рассматриваемого интенсив-ностного эффекта в пропускании (отражении) будем понимать разность коэффициентов пропускания (отражения) при намагниченном слое ( g * 0 ) и при отсутствии намагниченности ⁽ g = 0 ):

I r ( g ) = R ( g ) - R (0);           (2)

I t ( g ) = T 0 ( g ) — T 0 (0),            (3)

где T₀(g ), R 0 ( g ) — интенсивности прошедших и отражённых нулевых порядков дифракции.

Приведенные на рис. 2 спектры повторяют результаты работы [7]. В работах [7, 8] указано, что условия возникновения магнитооптического эффекта (2), (3) совпадают с условиями возбуждения волноводных TE-мод одним из порядков дифракции в намагниченном слое. Однако, сам факт возбуждения моды в [7, 8] не подтверждён. Кроме того, работы [7, 8] объясняют только провал в пропускании (рис. 2 а ), в то время как пик в отражении (рис. 2 б )являетсянеобъяснённым.

В общем случае резонансные свойства дифракционных структур определяются собственными квазиволноводными модами структуры [14]. Константы распространения собственных мод определяются полюсами матрицы рассеяния [14]. Резонансы возникают при приближении константы распространения одного из дифракционных

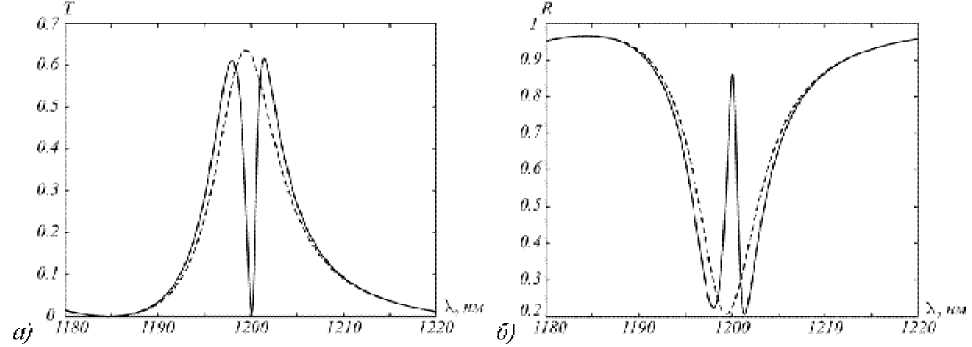
Рис. 2. Пропускание (слева) и отражение (справа) в случае намагниченного слоя (сплошная линия) и при отсутствии намагниченности (пунктирная линия)

порядков решётки к константе распространения собственной моды структуры. Дисперсионные соотношения для мод можно приближённо рассчитать, сделав следующие предположения: Во-первых, ввиду малости ширины отверстий в решётке можно считать, что над намагниченным слоем находится сплошной слой золота. Во-вторых, ввиду малости g , моды намагниченного слоя можно приближённо рассчитывать исходя из дисперсионных соотношений для TE- и TM-мод не-намагниченного планарного волновода. В первом приближении по g дисперсионное уравнение имеет такой же вид, как и для случая ненамагни-ченного волновода [8]. При сделанных предположениях константы распространения собственных мод структуры определяются константами распространения мод планарного немагнитного волновода, ограниченного сверху золотом, а снизу диэлектриком подложки.

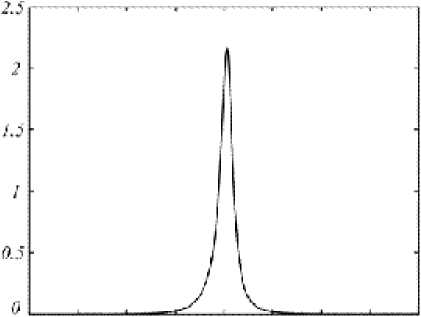
Резонанс на рис. 2 при λ = 1200 нм совпадает с условием возбуждения ТЕ-моды первым дифракционным порядком решётки [7]. При этом ТЕ-волны в отражённом и прошедшем поле отсутствуют. Для подтверждения факта возбуждения TE-моды были рассчитаны интенсивности TE-компонент электромагнитного поля на нижней и верхней границах намагниченного слоя. Для этого проводилось переразложение поля на нижней и верхней границах по TE- и TM-волнам ненамагниченного слоя. Это позволило рассчитать интенсивности TE- и TM-волн, соответствующих различным порядкам дифракции. На рис. 3 представлен спектр интенсивности TE-волны, соответствующей первому порядку дифракции. Спектр приведен для нижней границы намагниченного слоя, для верхней границы график имеет аналогичный вид. Резкий максимум интенсивности TE-волны в окрестности λ = 1200 нм подтверждает факт возбуждения в

??80      1190      1200 f2iu 3220

Рис. 3. Интенсивность TE-волны, соответствующей первому порядку дифракции на верхней границе намагниченного слоя рассматриваемой структуре моды TE-типа.

Рассмотрим TE- и TM-моды структуры с не-намагниченным слоем. В этом случае падающая волна с TМ-поляризацией может возбудить только ТМ-моды, а падающая волна с ТЕ-поля-ризацией — только TЕ-моды. В структуре с намагниченным слоем падающая волна с TМ- или ТЕ-поляризацией возбуждает моды обеих типов. При возбуждении падающей волной ТМ (ТЕ) типа моды слоя “противоположного типа” — TE (ТМ) происходит резонансное изменение характеристик отражённого и прошедшего полей.

Таким образом, резонансный магнитооптический эффект обусловлен возбуждением моды противоположного типа по отношению к поляризации падающей волны. Указанная мода возбуждается только в случае намагниченного слоя.

В случае на рис. 2 происходит перераспределение энергии между порядками, при котором энергия переходит из нулевого прошедшего порядка в нулевой отражённый порядок (рис. 2). Характер перераспределения зависит главным

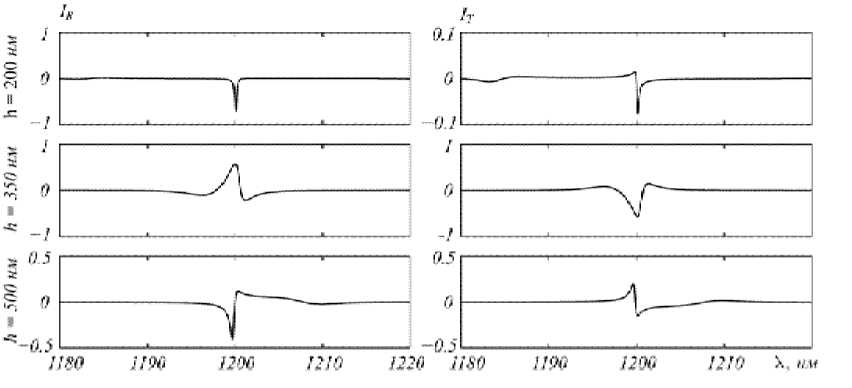
Рис. 4. Величина эффекта в отражении (слева) и пропускании (справа) при различных значениях высоты решётки (200 нм, 350 нм, 500 нм)

образом от таких параметров решётки как толщина и размер отверстия. Отметим, что изменение данных параметров не влияют на направления дифракционных порядков и поэтому в первом приближении не изменяют условий возбуждения мод в слое. Надлежащим выбором указанных параметров можно достичь как положительного, так и отрицательного изменения пропускания и отражения. На рис. 4 показаны величины интенсивностных эффектов (2), (3) в отражении и пропускании при разных значениях высоты решётки h_gr . Из рисунка видно, что в первом случае ( h_gr = 200 нм ) наблюдается провал, как в пропускании, так и в отражении, во втором случае ( h_gr = 350 нм ) энергия переходит из пропускания в отражение. В третьем случае ( h_gr = 500 нм ) виден более сложный характер перераспределения: при одних длинах волн в окрестности X = 1200нм энергия переходит из пропускания в отражения, при других — наоборот.

Возвращаясь к спектрам на рис. 2, отметим, что большой величины магнитооптических эффектов (2), (3) в данном случае удалось достичь за счёт совмещения магнитооптического эффекта с максимумом пропускания при X = 1200 нм для ненамагниченной структуры.

2.    ВЛИЯНИЕ СИММЕТРИИ НА МАГНИТООПТИЧЕСКИЕ ЭФФЕКТЫ

Проведем анализ свойств структуры на рис. 1, обусловленных ее симметрией. Как и ранее, рассматривается случай нормального падения волны с ТМ-поляризацией.

При повороте всей структуры на 180 градусов вокруг оси OZ у компонент отражённого и прошедшего поля изменяются только знаки. В этом случае интенсивности порядков и углы Фарадея и Керра, описывающие поворот плоскости поляризации, не изменяются. С другой стороны, поворот структуры эквивалентен замене направления вектора намагниченности на противоположное. При этом изменяется знак g в (1). Таким образом, при нормально падающей волне имеют место следующие соотношения:

ТЛg ) = T 0 ( - g ); R ( g ) = R ( - g ); (4)

I T ⁽ g ) = I T ^{( -} g ); I R ⁽ g ) = I R ^{( -} g ); ⁽⁵⁾

^ (g) = 00 (-g); o0 (g) = OR (-g), (6) где 00 ,00 — углы Фарадея и Керра, соответствующие нулевым порядкам дифракции. Угол Фарадея (Керра) определяет угол между главной осью эллипса поляризации в прошедшем (отражённом) пучке и направлением вектора поляризации в падающей волне [10]. С другой стороны эффекты, связанные с вращением плоскости поляризации, являются нечётными по величине g [10]:

0^Т 0 ( g ) = -0 T ( - g ); 0^R ( g ) = -0 R ( - g ). (7)

Согласно (6), (7)

O 0 ( ± g ) = O 0r ( ± g ) = 0.          (9)

Численный расчёт показывает выполнение условий (9) с высокой точностью. Рассматриваемая структура не проявляет магнитооптических свойств, связанных с вращением плоскости поляризации ни в прошедшем, ни в отражённом свете.

Согласно (5), интенсивностные магнитооптические эффекты в рассматриваемой структуре являются чётными по намагниченности. На рис. 5 показан модуль величины интенсивност-ного эффекта (3) в зависимости от g при X = 1200 нм . Значения на оси абсцисс на рис. 5 нормированы на величину Re ( g ) = 1.53 х 10 ^{- 2} при X = 1200 нм . Рис. 5 показывает, что рассматриваемый эффект является чётным по g . При малых g зависимость величины эффекта от g является квадратичной: I T ( g ) ~ ag ² . Аналогичные, квадратичные по гирации эффекты для однородных магнитных плёнок были экспериментально обнаружены в работах [15, 16]. Они были названы ориентационными из-за их зависимости от взаимной ориентации намагниченности плёнки и поляризации излучения. Описанные в [16] ориентационные эффекты являлись слабыми и наблюдались в отражённом свете. При этом относительное изменение коэффициента отражения в [16] составляло десятые доли процента. Рассматриваемый в данной работе эффект на несколько порядков сильнее.

При наклонном падении или для асимметричной структуры соотношения (6), (7), (9) не выполняются и в структуре должен появится магнитооптический эффект Фарадея.

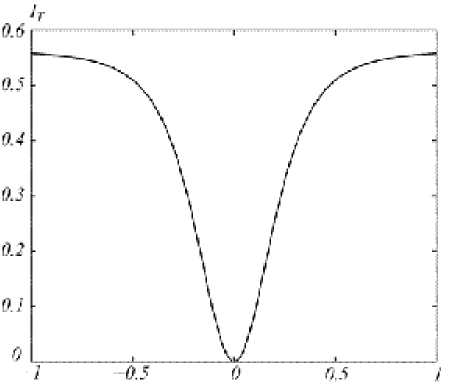
Рис. 5. Модуль величины интенсивностного эффекта в зависимости от намагниченности ( X = 1200 нм )

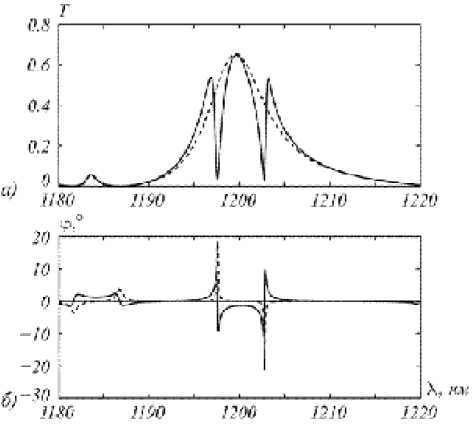
Рис. 6. Спектры в случае наклонного падения под углом 0.3 ° :

а – пропускание в случае намагниченного слоя (сплошная линия) и при отсутствии намагниченности (пунктирная линия); б – угол Фарадея (сплошная линия) и эллиптичность (пунктирная линия)

При нормальном падении волны на струкТУРУ дифракционные порядки с номерами ± m распространяются под одинаковыми углами и их влияние на спектр пропускания, ввиду симметрии, происходит при одной и той же длине волны. При наклонном падении модули констант распространения k_{x , m} для порядков с номерами ± m будут различаться. Соответственно, их влияние на спектр будет происходить при

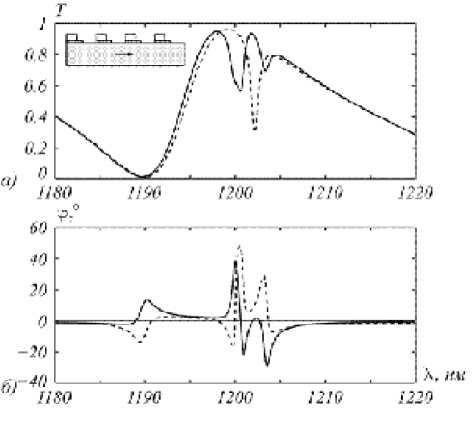
Рис. 7. Спектры несимметричной структуры (врезка) при нормальном падении:

а – пропускание в случае намагниченного слоя (сплошная линия) и при отсутствии намагниченности (пунктирная линия); б – угол Фарадея (сплошная линия) и эллиптичность (пунктирная линия)

двух различных длинах волн. Расчётный спектр пропускания приведен на рис. 6 а и показывает наличие двух разнесённых минимумов. При наклонном падении становится отличным от нуля угол Фарадея (рис. 6 б ). Значения угла Фарадея на рис. 6 б достигают ± 10 ° . Следует отметить, что вблизи резонансов угла Фарадея эллиптичность также принимает значительные значения (около ± 20 ° ). Тангенс угла эллиптичности определяет отношение длин осей эллипса поляризации. Соответственно только при малых углах эллиптичности угол Фарадея можно рассматривать как угол поворота плоскости поляризации падающей волны.

В рассматриваемой структуре фактически отсутствует эффект Керра. Это связано с тем, что металлическая решётка работает как поляризатор, не позволяя выйти волнам с ТЕ-по-ляризацией из намагниченного слоя в область над структурой.

Использование несимметричной решётки также позволяет создать асимметрию в распределении энергии между порядками с номерами ± m . Указанная асимметрия даже при нормальном падении приведёт к появлению эффекта Фарадея. В настоящей работе исследовалась несимметричная структура, состоящая из двух бинарных дифракционных решёток и намагниченного слоя (врезка к рис. 7). На рис. 7 приведены спектры пропускания и угла Фарадея указанной структуры, рассчитанные при нормальном падении волны с ТМ-поляризацией и следующих параметрах структуры: период d = 552 нм , толщина намагниченного слоя h = 1930 нм , толщина и размер отверстий верхней решётки h ^ ( ' ) = 200 нм , r ⁽¹⁾ = 359 нм , толщина и размер отверстий нижней решётки h g 2) = 10 нм , r ⁽²⁾ _ 248 нм . Значения резонансов углов Фарадея составляют от 10 до 40 градусов. В частности при X = 1200 нм угол Фарадея составляет более 35 ° при эллиптичности менее 1 ° . На этой же длине волны структура обладает интенсив-ностным эффектом (3), причем изменение пропускания составляет более 25%. Следует отметить, что резонансы угла Фарадея в несколько раз больше полученных в работах [2, 5, 6] для аналогичных гетероструктур со слоем, намагниченным в полярной геометрии.

ЗАКЛЮЧЕНИЕ

При определенных условиях изменение величины гирации магнитного слоя дифракционной структуры на рис. 1 вызывает магнитооптический эффект, заключающийся в изменении коэффициентов пропускания и отражения. Как и ориентационные магнитооптические эффекты для однородных плёнок, данный эффект квадратичен по намагниченности, однако на несколько порядков величины превосходит их. В случае падения TM-поляризованного света спектральное положение и величина этого эффекта определяются условиями возбуждения ТЕ-мод в диэлектрическом слое. Эффект связан с перераспределением энергии вследствие возбуждения волноводной TE-моды в намагниченном слое.

При наклонном падении и в структуре с асимметричной дифракционной решёткой существуют резонансные эффекты Фарадея, связанные с вращением плоскости поляризации прошедшей волны.

Рассмотренные структуры имеют прикладную значимость и могут быть использованы в новых устройствах интегральной оптики для модуляции интенсивности света посредством изменения внешнего магнитного поля.

Работа выполнена при поддержке грантов РФФИ № 09-07-92421, 08-07-99005, 0701-96602, 09-07-12147, гранта Президента РФ № НШ-3086.2008.9, “Фонда содействия отечественной науке”, Российско-американской программы “Фундаментальные исследования и высшее образование” (RUXO-014-SA-06).