Исследование шероховатости поверхностей конических роликовых подшипников

Долговечность подшипника в значительной степени определяется работоспособностью тел качения – роликов. Наиболее целесообразной формой рабочего торца конического ролика и упорного борта внутреннего кольца является сфера. При этом контакт происходит по площади, что обеспечивает благоприятное распределение напряжений.

Требования к качеству конических роликовых подшипников постоянно повышаются. Твердость рабочей поверхности ролика после термической обработки составляет 58…63 HRC. На основании анализа существующих схем шлифования и сферошлифовальных станков по критериям универсальности, производительности и качеству обработки рассмотрено исследование процесса непрерывного шлифования на станке для шлифования сферических торцов конических роликов подшипников качения, обеспечивающее заданное качество обработки при высокой производительности и в широком диапазоне радиусов сферы.

Качество поверхности конических роликов с точки зрения шероховатости поверхности во многих случаях является определяющим фактором, влияющим на долговечность и надёжность роликовых подшипников при их эксплуатации.

МЕТОДИКА ИССЛЕДОВАНИЙ

Технология производства конических роликов предусматривает на заключительных операциях технологического процесса применение операций шлифования. Окончательную обработку наружной конической поверхности дорожки качения осуществляют на бесцентрово- шлифовальных станках СВААКМ 25/1 абразивными кругами на вулканитовых связках (14А6НСМ2В1). Режимы шлифования были следующие:

• -    скорость абразивного круга 55 м/с;

• -    скорость вращения ведущего круга 70 м/мин;

• -    снимаемый припуск 0,01 мм;

• -    скорость продольной подачи 300 мм/мин;

• -    обработку проводили с охлаждением и периодической правкой алмазным карандашом.

Торцы роликов обрабатывались на двухстороннем торцешлифовальном станке ЗАЗ43 абразивными кругами размером 600 х 63 х 305 и характеристиками 14А 25П СМ1 10Б. Обработка торцов производилась на следующих режимах:

• -    окружная скорость шлифовального круга 35 м/с;

• -    общий припуск 0,01 мм;

• -    скорость подачи ролика в зону обработки

• 2,5 м/мин;

• - шлифование осуществлялось с подачей смазывающей охлаждающей жидкости (СОЖ) и периодической правкой круга алмазом в оправке.

На первом этапе исследования шероховатости поверхностей были выполнены на специализированном исследовательском комплексе, включающем профилограф модели SJ – 201P, компьютер и соответствующее программное обеспечение, позволяющее записывать и обрабатывать профилограммы. На торцах ролика профилограммы снимались в радиальном и окружном направлениях.

Одной из первых задач по повышению качества обработки сферических торцов роликов является подбор инструмента. Особенностью инструмента сферошлифовального станка является то, что он после правки по радиусу образует рабочую зону.

Шлифовальный круг профилируется по заданному радиусу алмазным карандашом. Существует два способа правки круга: от приводной головки со стороны рабочей зоны и по копиру в стороне (перпендикулярно или противоположно) от рабочей зоны.

Правка с приводной головки производится алмазным карандашом, расположенным в специальном гнезде сепаратора и закрепленным в одном из подающих дисков. Движение алмаза при правке осуществляется от гидроцилиндра. Карандаш устанавливается по середине жёлоба, образованного дисками приводной головки, и тем самым проходит через ось шлифовального круга.

Для правки с противоположной стороны от рабочей зоны применяют специальное приспособление, в котором алмазный карандаш крепится на скалке, а от гидроцилиндра получает качательное движение по радиусу. Скорость правки регулируется скоростью перемещения гидроцилиндра. В зависимости от типа обрабатываемого ролика изменяется положение скалки и соответственно радиус движения алмаза. Правка шлифовального круга осуществляется с продольной подачей 0,5 – 0,6 м/мин.

При определении радиуса правки шлифовального круга учитывалась жёсткость приводной головки, так как в процессе обработки торцов роликов под воздействием усилий резания детали вдавливались в пространство между дисками.

Радиус правки в данном случае определялся по формуле:

R _пр = R _д + h – k – T, где R _д - радиус дисков приспособления, мм;

• h – вылет ролика над дисками в месте загрузки, мм;

• k – величина осевого перемещения ролика в дисках, зависящая от податливости приспособления, принимает значение 0,2 – 1,0 мм;

T – припуск на обработку сферического тор- ца ролика, мм.

При исследованиях шлифовальный круг профилировался корригированным радиусом обработки:

R = Rc – ΔR, где Rc – радиус сферы, заданный чертежом, мм;

Δ R – величина корригирования радиуса, мм, определяемая по формуле:

ДпЛд 2 -г_в²-^

Д^= п=^=--- Н=>

1к 2 -Г в² -ДП-|Д²-Г²

где Δ П – величина погрешности профиля сферы торца, мм;

• r _p – радиус обрабатываемого торца ролика, мм ;

r _в – радиус технологической выемки на торце ролика, мм.

При исследованиях применялась смазочно-охлаждающая жидкость от цеховой системы. В зону шлифования СОЖ подаётся в количестве 7 л/мин.

Влияние режимов обработки на погрешность сферы при непрерывном шлифовании сферических торцов исследовались на станке модели БСШ-200М [1]. После выявления оптимальных режимов обработки проводились исследования точности, устойчивости и стабильности процесса.

Шлифовальный круг профилировался рассчитанным радиусом обработки и балансировался. Наблюдение за процессом обработки проводилось в течение 3-4 часов межправочного периода работы станка.

В процессе экспериментов исследовались факторы, характеризующие точность профиля сферической поверхности торца ролика: радиус сферы, торцовое биение, огранка и шероховатость сферического торца ролика.

На следующем этапе были выполнены исследования шероховатости выбранных участков рабочей и торцовых поверхностей ролика с помощью оптико-электронного комплекса и разработанной методики на основе использования ква-зиоптимального корреляционного алгоритма [2].

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

При шлифовании роликов 7606 на станке ВШ-680 корригированным радиусом обработки были получены хорошие результаты, а именно, в поле допуска находилось торцовое биение, огранка и шероховатость. Ролики шлифовались без правки круга в течение трёх часов, и при этом средняя величина радиуса сферы постоянно находилась в допуске. Исследование высоты микронеровностей по длине рабочей поверхности ролика показало, что среднее арифметическое отклонение профиля Ra по этой длине изменяется незначительно от: Ra =0,105 мкм до Ra =0,094 мкм.

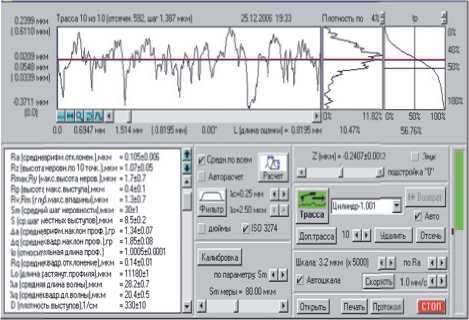
Рис. 1. Вид интерфейса с профилограммой и параметрами шероховатости для рабочей поверхности ролика

Исследование высоты микронеровностей поверхности торцов ролика во взаимно перпендикулярных направлениях показало, что параметр Ra по этим направлениям практически не отличается друг от друга для одной и той же поверхности.

Однако на разных торцах ролика формиру- бинарные изображения участков рабочей поверхности ролика, а также графики изменения коэффициента корреляции и корреляционные поверхности приведены на рис. 5 – 9. Результаты измерения средней амплитуды переменной составляющей корреляционных функций для выделенных участков дали следующие значения от Uср = 17,9 отн. ед.; до Uср = 16,3 отн. ед.;

Таким образом, все найденные значения U_ср попадают в диапазон 6 – 21 отн. ед., что предполагает использование зависимости Ra =0,0065 х и ср - 0,02 мкм для определения среднего арифметического отклонения профиля рабочей поверхности ролика. Подставляя найденные значения U_ср в это выражение, получим:

для участка №1 – Ra = 0,096 мкм;

для участка №2 – Ra = 0,089 мкм;

для участка №3 – Ra = 0,086 мкм;

для участка №4 – Ra = 0,094 мкм;

для участка №5 – Ra = 0,087 мкм.

Для определения доверительных интервалов I _в , в которые попадает случайная величина U_ср , зададим вероятность распознавания шероховатости поверхности, равной P =0,99. Про-

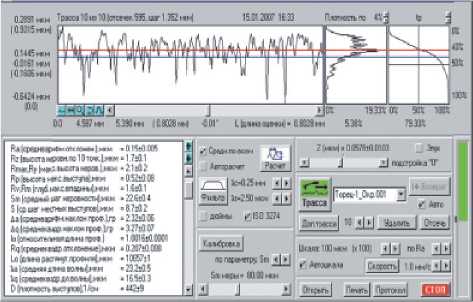
Рис. 2. Вид интерфейса с профилограммой и параметрами шероховатости для торца ролика 1 в радиальном направлении

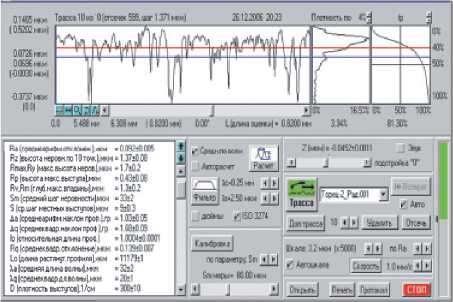
Рис. 3. Вид интерфейса с профилограммой и параметрами шероховатости для торца ролика 2 в осевом направлении

ется различный микрорельеф. При этом на торцевой поверхности №1 величина Ra составила 0,13 мкм в радиальном направлении и 0,15 мкм в осевом направлении, а для торцовой поверхности №2 Ra = 0,09 мкм в радиальном направлении и Ra = 0,105 мкм в осевом направлении. Отмеченная особенность микрорельефа торцов ролика приведена на рис. 4. Такое распределение высотных параметров микрорельефа по торцам ролика связано с тем, что угол захода конуса на шлифовальных кругах разный и в связи с этим с обрабатываемых торцовых поверхностей снимается различный припуск. В частности, с торца №1 снимается больший припуск.

На следующем этапе исследования шероховатости поверхностей ролика выполнены с помощью оптико-электронного комплекса и разработанной методики [2]. Полутоновые и

1 торец                       2 торец

Рис. 4. Шероховатость торцовых поверхностей ролика

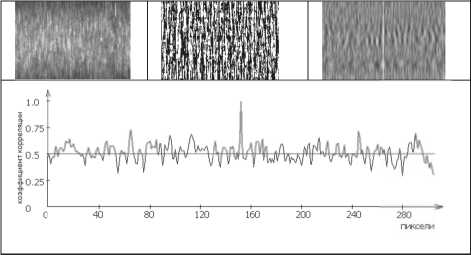
Рис. 5. Результаты обработки изображения участка №1 рабочей поверхности ролика

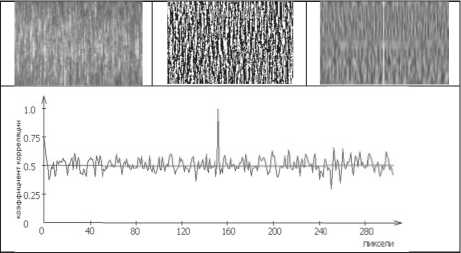
Рис. 6. Результаты обработки изображения участка №2 рабочей поверхности ролика

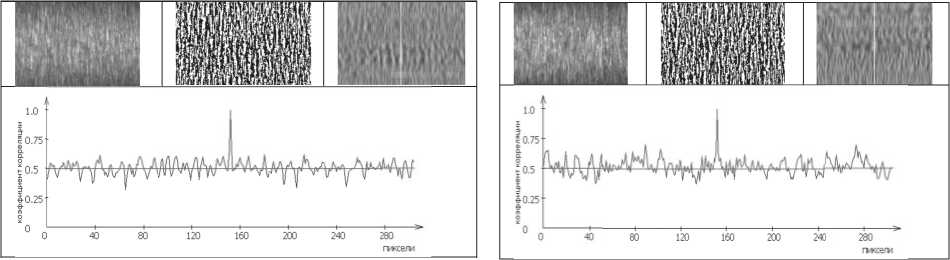
Рис. 7. Результаты обработки изображения участка №3 рабочей поверхности ролика

Рис. 8. Результаты обработки изображения участка №4 рабочей поверхности ролика ведённые исследования с использованием ква- зиоптимального корреляционного алгоритма позволили найти величины среднего квадратического отклонения (СКО) с от иср для образцов с шероховатостями:

Ra = 0,13мкм – U_ср =21,6 отн. ед.,

• с = 2,0 отн. ед.;

Ra = 0,084мкм – U_ср =13,2 отн. ед.,

• с = 0,8 отн. ед.;

Ra = 0,048мкм – U_ср =10,8 отн. ед.,

• с = 0,6 отн. ед.;

Ra = 0,025мкм – U_ср =6,8 отн. ед., с = 0.07 отн. ед.

При этом также было установлено, что сама случайная величина Uср подчиняется нормальному закону распределения. В этом случае число СКО, которое нужно отложить вправо и влево от центра рассеивания для того, чтобы вероят- ность попадания случайной величины Uср в полученный интервал была P=0,99, составляет tр = 2,576.

Для каждого образца было обработано по 30 изображений с различных участков иссле- дуемой поверхности, то есть n = 30. Тогда СКО оценки при определении Uср формуле:

с определяется по

^с t = n^

.

Следовательно, для образцов поверхности с шероховатостью Ra = 0,13 мкм имеем с _t =0,37 отн.ед., с шероховатостью Ra = 0,084

мкм - с _t = 0,15 отн.ед., с шероховатостью Ra = 0,048 мкм - с _t = 0,11 отн. ед. и с шероховатостью Ra = 0,025 мкм - с _t =0,013 отн. ед. Через величины t р и с _t доверительный интервал выражается в виде:

^АР = ( U cp - 1 р Х с t ; U p + 1 _р х с t ).          (2)

Округляя вычисленные значения I _р = t _в х с_t в сторону увеличения, получим для отмеченных значений шероховатости следующие величины доверительных интервалов:

Ra = 0,13мкм - 1 _в = 1,0 отн. ед.; 20,6 отн. ед. ^ U_ср ≤ 22,6 отн. ед.;

Ra = 0,084мкм - 1 _в = 0,4 отн. ед.; 12,8 отн. ед. ≤ U_ср ≤ 13,6 отн. ед.;

Ra =0,048мкм - 1 _в = 0,3 отн. ед.; 10,5 отн. ед. ^ U_ср ≤ 11,1 отн. ед.;

Ra = 0,025мкм - 1 _в = 0,03 отн. ед.; 6,77 отн. ед. ≤ U_ср ≤ 6,83 отн. ед.

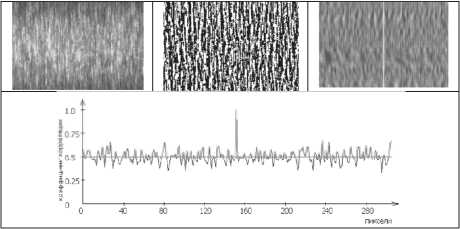
Рис. 9. Результаты обработки изображения участка №5 рабочей поверхности ролика

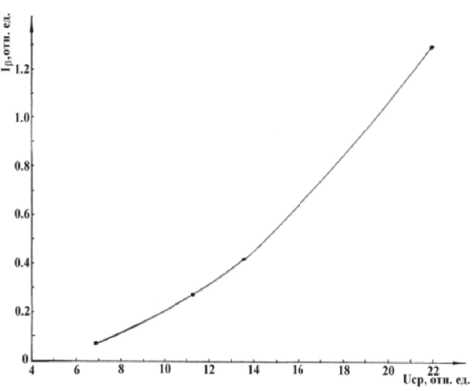
Рис. 10. Зависимость I _в от средней амплитуды переменной составляющей корреляционной функции U_ср при использовании формата 320 х 240 пикселей для изображения поверхности

Как видно из приведенных данных, доверительные интервалы для U_ср с увеличением шероховатости возрастают, и что очень важно, не перекрываются. График зависимости I _в = f ( и ср ) приведён на рис. 10.

Согласно приведённому графику, зависимость I р = f ( и ср ) имеет нелинейный характер. Используя метод наименьших квадратов, для данного доверительного интервала была получена аналитическая зависимость

Iв = (3,4 х U_cp² + 14,4 х и_ср + 1) х 10^-3. (3)

Подставляя в найденное выражение U_ср , получим:

от Iв = 1,35 отн. ед., до иср = 19,25 отн. ед., следовательно, Ra = 0,088 мmкaxм и Ra = 0,105 мкм; min max для участка №2 - Iв = 1,19 отн. ед., иср . = 15,51 отн. ед. и Uср = 17,89 отн. ед., следоватеmльn -но, Ra = 0,081 мкmмax и Ramax = 0,096 мкм;

для участка №3 - I _в = 1,14 отн. ед., и ср . = 15,16 отн. ед. и U_ср = 17,44 отн. ед., следовате ^m ль ⁿ -но, R_a = 0,079 мк ^m м ^ax и R_amax = 0,093 мкм;

для участка №4 - I _в = 1,29 отн. ед., и ср . = 16,21 отн. ед. и U_ср = 18,79 отн. ед., следов ^m а ⁿ тельно, R_a = 0,085 м ^m к ^a м ^x и R_a = 0,102 мкм;

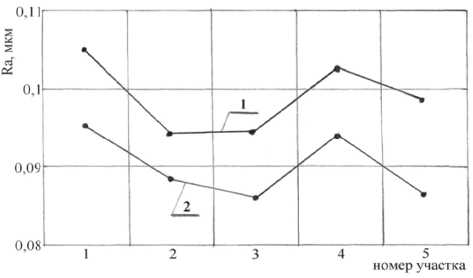
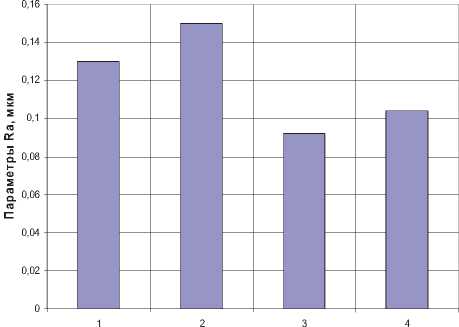
Рис. 11. Значения Ra на выделенных участках рабочей поверхности:

1 – полученные с помощью профилографа, 2 – полученные с помощью оптико-электронного комплекса для участка №5 - Iв = 1,16 отн. ед., иср . = 15,340 отн. ед. и Uср = 17,66 отн. ед., следоmваn -тельно, Ra = 0,08 мmкaмx и Ra = 0,095 мкм;

Найде ^m н ⁱ н ⁿ ые значения с ^m р ^ax еднего арифметического отклонения профиля рабочей поверхности ролика вполне согласуются со значениями, определёнными с помощью профилографа модели SJ – 201P. Графики зависимости средних значений Ra от исследуемого участка рабочей поверхности, полученные с помощью профилографа и оптико-электронного исследовательского комплекса, приведены на рис. 11. Незначительное расхождение ~0,1% в значениях Ra , полученных разными методами можно объяснить невозможностью абсолютно точно совмещения участков поверхности для записи профилограмм и видеосъёмки и, кроме того, разной размерностью профилограмм и видеоизображений.

Полутоновые и бинарные изображения характерных участков торцовых поверхностей ролика №1 и №2, а также графики изменения коэффициента корреляции и корреляционные поверхности для этих участков приведены на рис. 12 и 13.

Результаты измерения средней амплитуды переменной составляющей корреляционных функций для выделенных участков дали следующие значения:

• -    для торцового участка №1 U_ср = 23,6 мкм,

• -    для торцового участка №2 U_ср = 17,5 мкм.

  

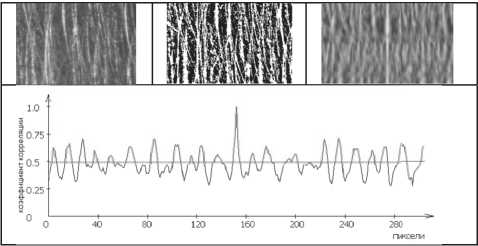
  Рис. 12. Результаты обработки изображения торцовой поверхности ролика №1

  
  
  

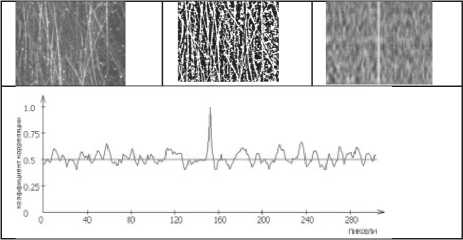
  Рис. 13. Результаты обработки изображения торцовой поверхности ролика №2

  
  

Используя найденные значения U_ср для определения I _e , Ra , R a . и R a по выражению (3) определили, что для т ^m о ⁿ рцов ^m о ^ax й поверхности №1 Ra = 0,13 мкм, R_a = 0,12 мкм и R_a =0,15 мкм. Для торцовой по ^m в ⁿ ерхности №2 Ra^m = ^ax 0,095 мкм, R_a = 0,086 мкм и R_a =0,10 мкм.

^mn Таким образом, ^ma в ^x этом случае, параметры шероховатости торцовых поверхностей ролика, найденные с помощью измерительного оптикоэлектронного комплекса, вполне согласуются с аналогичными параметрами, измеренными с помощью профилографа модели SJ-201P.

ВЫВОДЫ

Анализ полученных данных показывает, что с увеличением шероховатости поверхности средняя амплитуда колебания автокорреляционной функции Аср повышается. Обработка экспериментальных данных позволила получить регрессионные зависимости, связывающие амплитуду автокорреляционной функции и параметры шероховатости поверхности образца.

Получены регрессионные уравнения идентификации микрогеометрии поверхности прецизионных деталей подшипника на основе вычисления номинальных значений параметров шероховатости Ra , Rp , Rmax , S_m , t_m в зависимости от средней амплитуды автокорреляционной функции, вычисленной по изображению исследуемой поверхности. Для базового окна размером эталона 6х6 получены следующие аналитические зависимости:

Ra = 0,004 ^х А с - 0,016, мкм

Rp = 0,17 + 0,01 ^Х А с _р, мкм

Rmax = 0,88 + 0,052 ^х А ср , мкм (3.1)

Sm = 46,8 - 0,91 х Аср, мкм tm = 0,7 + 3,3 х Аср, %.

Для базового окна размером эталона 8х8 получены следующие аналитические зависимости:

Ra = 0,0391· А_ср – 0,4794, мкм

Rp = 0,16 + 0,013 ^х А_ср, мкм

Rmax = 0,84 + 0,056 х А ср , мкм     (3.2)

S m = 47,1 - 0,9 ^х А ср , мкм t m = ^0,8 + ^{3,5 Х} А ср , %

Для базового окна размером эталона 9х9:

Ra = 0,0644 · А_ср – 0,8082, мкм

Rp = 0,14 + 0,015 ^х А_ср, мкм

Rmax = 0,82 + 0,058 х А ср , мкм    (3.3)

S m = 46,5 - 0,93 ^х А_ср, мкм t m = 0,85 + 3,6 ^х А ср , %.

Анализ полученных данных показал, что с увеличением формата эталона от 6 × 6 до 9 х 9 пикселей разница в средней амплитуде переменной составляющей корреляционной функции Аср для образцов с различной шероховатостью остаётся постоянной.