Исследование сил резания, возникающих при ортогональном свободном точении сплава Д16, с помощью методик аналитического и конечно-элементного анализа

Процесс механической обработки материалов лезвийным инструментом сопровождается противодействующими силами, знание которых необходимо для выполнения расчетов на прочность, жесткость и виброустойчивость элементов конструкции станков и режущих инструментов.

Кроме того существует подход к оценке действующей температуры в зоне резания при точении, основывающийся на знании величин плотностей тепловых потоков, определить которые возможно при условии известных величин составляющих силы резания. Как известно, на формирование состояния поверхностного слоя деталей оказывают влияние силовой и температурный факторы. Причем, если температура в зоне резания достигает значений, соответствующих значениям критических точек аллотропических превращений в поверхностном слое материале заготовки, то влияние температуры на формирование поверхностного слоя существенно возрастает.

Остаточные напряжения, формируемые в поверхностном слое заготовок при резании и являющиеся одним из основных параметров, определяющих качество обработки, возникают в результате воздействия силового и температурных полей в зоне резания [1, 2, 3]. Также известно, что остаточные напряжения в значительной степени влияют на сопротивление усталости деталей. Существуют методики оценки остаточных напряжений в поверхностном слое заготовок наведенных после их

обработки. Такие методики обычно требуют знание величины силы резания и температуры, действовавшей в зоне резания [4].

Поэтому необходимо проводить исследования силы резания, применять различные методики для ее оценки, находить их недостатки и искать пути совершенствования существующих методик.

МЕТОДИКА АНАЛИТИЧЕСКОГО ОПРЕДЕЛЕНИЯ СИЛЫ РЕЗАНИЯ

При создании методики авторы работы [5] использовали схему распределения сил в зоне резания, которая была составлена Юджином Мёрчантом (M. Eugene Merchant). Для исследования, представленного в данной работе, в схему распределения сил были внесены изменения в виде добавленных составляющих силы резания, таких как N₃ и F₃ [6, 7]. Необходимость их присутствия объясняется наличием у неидеального режущего клина площадки его контакта по задней поверхности с заготовкой. Распределение сил показано на рис. 1.

В соответствии с методикой, изложенной в работе [5], касательная сила (сила сдвига), возникающая в плоскости сдвига АВ (рис. 1), определяется по формуле:

Р. =АВ■b■ тсд,

где b - ширина срезаемого слоя, Т_сд. - касательные напряжения, возникающие в зоне сдвига, АВ

– длина плоскости сдвига, которую просто вычислить, зная глубину резания t и угол сдвига β ₁ :

t

АВ =--—.

sin^

Угол сдвига β ₁ можно определить, используя зависимость А.Н. Резникова [7]:

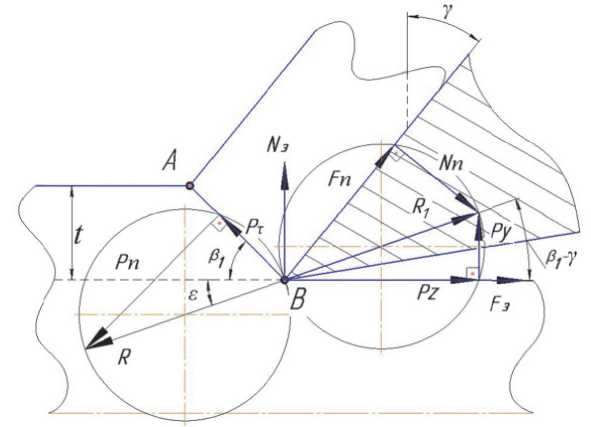
Рис. 1. Схема распределения сил в зоне резания

cosy

"'^  /=7=s^=T •   ⁽¹⁾

где к - коэффициент усадки стружки.

Определив силу сдвига Pт, по зависимости, представленной в работе [8] возможно вычислить величину нормальной силы Pn , перпендикулярной к Pт. Равнодействующей этих двух сил является сила R, а её реакцией, направленной в режущий клин - сила R 1 (R = R 1). Зная силу R 1 можно определить главную, тангенциальную Pz и радиальную Ру составляющую силы резания, а также нормальную силу Nn и силу трения Fn, действующие на передней поверхности режу- щего клина.

В методике, изложенной в работе [5] определение тангенциальной P_z и радиальной силы резания Р у сведено к следующим формулам: _{р =} ^р ■ ^{cos ( р} _ц - т ) _{р =} ^р ■ ^sin ( Р_н - у ) ^{Z    cos ( р} 1 + Р ^ ^- у ^{) У cos (} р _г + Р ^ ^- у ⁾

где Р_ц - угол действия силы давления [9].

Но как уже было сказано выше, к данным формулам были добавлены слагаемые в виде силы трения задней поверхности режущего клина о заготовку F₃ и силы упруго-пластического взаимодействия задней поверхности режущего клина с заготовкой N₃ . Оценить величину данных сил помогли рекомендации А.Н. Резникова [7], согласно которым сила F₃ принимается примерно равной силе N₃ и может быть определена по зависимости:

F ₃ « 0,252 ■ о₅ ■ b ■ 1 _Э , где ст B - предел прочности обрабатываемого материала, b - ширина срезаемого слоя, 1 З - длина участка контакта задней поверхности режущего клина с заготовкой.

При проведении исследования угол Р_ц был получен с использованием формулы Юджина

Мёрчанта [5], что стало возможным благодаря известному углу сдвига (1):

Р 1

^{л Р}н , т 4^-У ⁺ 2'

Далее, для определения всех представленных на рис. 1 сил, необходимо рассчитать значение силы сдвига P _т . Ее определение сводится к умножению величины касательных напряжений Т_сд . в плоскости сдвига AB на площадь плоскости сдвига. Для того чтобы определить величину касательных напряжений в плоскости сдвига AB авторами работы [5, 8] было использовано уравнение Джонсона-Кука:

^т ^^д =;т5 [^л+s (;^) " ][^1+cln Э^1-^,

0 при Т <ТС т-Т т _т при Тс < Т < ТпЛ Тпл Т С

1 при Т > Тпл где 8Сд - деформация сдвига; £Сд - скорость деформации сдвига; £0 - справочная скорость пластической деформации (обычно, перед тем как определять коэффициенты зависимости, данное значение принимается равным 1 с-1), что упрощает вычисление напряжений пластического течения по уравнению; Тс - справочная температура (принимается обычно равной комнатной температуре); Тпл - температура плавления обрабатываемого материала; А - предел текучести материала, соответствующий справочным скоростям деформации и температуры; B - модуль деформационного упрочнения; n -показатель степени деформационного упрочнения; m - экспонента термопластикации; C - показатель чувствительности к скорости деформирования.

РАЗРАБОТКА КОМПЬЮТЕРНОЙ МОДЕЛИ ДЛЯ ПРОВЕДЕНИЯ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ

В универсальной программной системе конечно-элементного анализа ANSYS была разработана компьютерная модель ортогонального свободного точения алюминиевого сплава Д16, применительно к установившемуся процессу резания. Модель представлена в виде двух виртуальных тел заготовки и режущего клина, для каждого из которых задано свое кинематическое описание движения и свое описание материала внутри компьютерной программы.

ОПИСАНИЕ ГЕОМЕТРИИ ВИРТУАЛЬНЫХ ТЕЛ КОМПЬЮТЕРНОЙ ПРОГРАММЫ

Заготовка имеет следующие геометрические параметры: высота 5 мм, ширина 2 мм, длина 10 мм. Режущий клин имеет передний угол γ = 12°, ширина режущего клина 4 мм, а радиус скругления режущей кромки составляет 0,025 мм. Две другие кромки виртуального тела режущего клина имеют скругление 0,25 мм. Это связано с задачей корректного наложения сетки конечных элементов в данных областях режущего клина (рис. 2).

ОПИСАНИЕ МАТЕРИАЛА ВИРТУАЛЬНЫХ ТЕЛ

Помимо геометрических данных заготовки и режущего клина, в роли исходных данных для вычислений выступили также описания материалов заготовки и режущего клина при использовании модели пластичности Джонсона-Кука и модели разрушения Джонсона-Кука, уравнение которой приведено ниже:

ё/ = [^ + ^ехр (03 ■ ^)] ■ [1 + 041п (|)] ■ (1 + О5Т), где σm является средней величиной по трем главным напряжениям, О - эквивалентные напряжения, полученные по критерию пластично- сти фон Мизеса, Еу - эквивалентная деформация при разрушении, а Di – это коэффициенты, получаемые по результату экспериментов.

КИНЕМАТИЧЕСКОЕ ОПИСАНИЕ ДВИЖЕНИЯ ВИРТУАЛЬНЫХ ТЕЛ

Выполненные расчеты, что при задействовании аналитической методики определения силы резания, что при использовании компьютерной модели, были проведены для режимов обработки сплава Д16, соответствующих подаче 0,47 мм/об и 1 мм/об при глубине резания составляющей 2 мм и скорости резания менявшейся в диапазоне от 15 до 75 м/мин.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

Прежде всего, стоит отметить, что на величину силы резания при использовании аналитической методики, оказывает большее влияние изменение коэффициента усадки стружки, нежели изменение скорости резания. Изменение скорости резания влечет к изменению касательных напряжений, в плоскости сдвига. В свою очередь, это изменение, при всех исходных данных представленного исследования оказалось небольшим и для увеличения точности прогнозируемой величины силы резания необходимо знание изменения усадки стружки в зависимости от скорости и глубины резания. В представленной работе коэффициент усадки стружки был принят постоянным для всех скоростей резания, т.е. не учитывалось его изменение в зависимости от скорости резания.

Ниже представлены графики изменения составляющих силы резания и их результирующей, полученные посредством компьютерной модели (рис. 3 и 4).

Далее приведена таблица со средними значениями сил, вычисленными с помощью аналитической методики и сравненными с аналогичными значениями, полученными с помощью компьютерной модели (табл. 1).

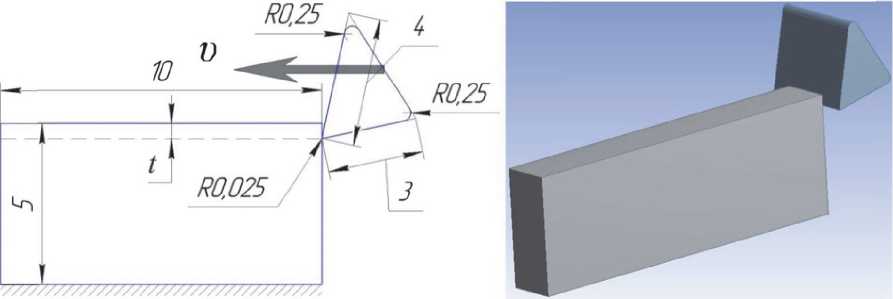
Рис. 2. Кинематическая схема компьютерной модели и изометрия виртуальных тел заготовки и режущего клина

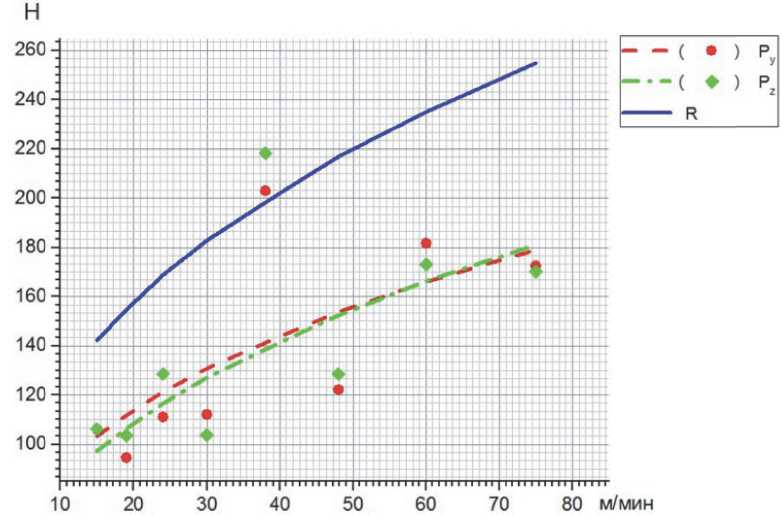
Рис. 3. Зависимость составляющих силы резания от скорости резания при подаче S = 0,47 мм/об

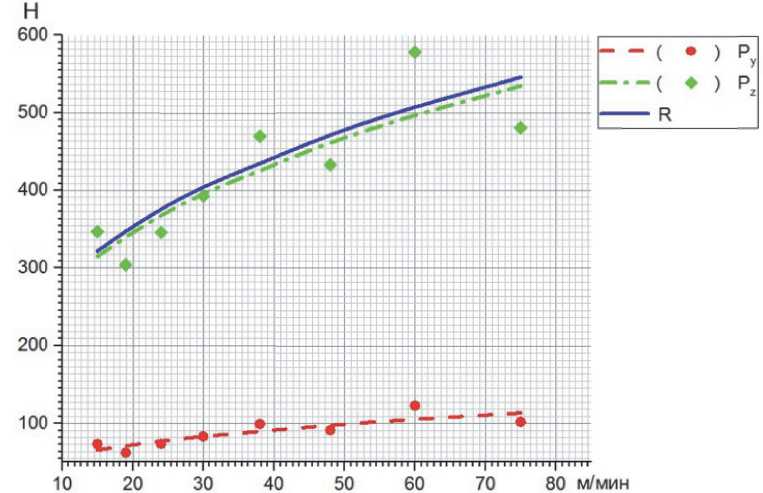
Рис. 4. Зависимость составляющих силы резания от скорости резания при подаче S = 1 мм/об

Таблица 1. Величины средних значений сил при ортогональном свободном точении сплава Д16, при глубине резания t = 2 мм на диапазоне скоростей резания 15–75 м/мин

S = 0,47 мм/об
сила, Н	комп. модель	мат. модель	д, %
Py	138	175	21
Pz	141	167	15
R	198	242	18
S = 1 мм/об
Py	89	98	10
Pz	419	461	9
R	428	471	9

ВЫВОДЫ

Были получены зависимости составляющих силы резания при ортогональном свободном 4 точении сплава Д16 с помощью разработанной . компьютерной модели.

Величины средних значений составляющих силы резания, полученные с помощью компью- 5. терной модели, были сравнены с аналогичными значениями, полученными с помощью аналитической методики, использование которой при исследовании сопровождалось внедрением некоторых рекомендаций и зависимостей А.Н. ^6. Резникова. Разница полученных результатов лежит в диапазоне 9-21%.

No. 10. P. 773–776.

RESEARCH OF CUTTING FORCES AT ORTHOGONAL FREE TURNING OF D16 ALLOY BY MEANS OF TECHNIQUES ANALYTICAL AND A TERMINATING ULTIMATE ANALYSIS