Исследование спектральной устойчивости обобщенных методов Рунге-Кутты применительно к численному интегрированию начальной задачи для уравнения переноса

Многие задачи механики сплошной среды имеют решения с большими градиентами, например в случае ударного нагружения [1, 2 и другие], что обуславливает актуальность проблемы разработки надежных, устойчивых методов численного интегрирования начально-краевых задач с ярко выраженными локальными эффектами решения [см. 1, 3, 4 и другие]. Большую достоверность определения поведения неизвестных функций в подобластях с большими и быстроосциллирующими градиентами обеспечивают методы, обладающие высокими порядками точности, приводящие к приемлемым результатам даже на «грубых» сетках [1].

В одномерных случаях хорошо зарекомендовали себя неклассические методы Рунге–Кутты (МРК) [5] для эффективного численного интегрирования начальных и краевых задач с жесткими дифференциальными

уравнениями, решения которых обладают указанными выше особенностями, Поэтому вопрос о целесообразности обобщения этих методов на многомерные случаи был вполне естественным, что и было проделано автором в [6, 7 и других].

Эффективность такого обобщения, в частности, заключается в том, что в начально-краевых задачах математической физики и механики дискретизация области интегрирования осуществляется в нетрадиционной последовательности. Так как область определения в нестационарных (динамических) задачах, кроме пространства, включает время, то методы численного решения предполагают дискретизацию разрешающей системы уравнений и по этой переменной. Возможны два способа дискретизации: одновременное [8] и последовательное пространственно-временное деление области интегрирования [9–12 и другие]. Используемые к настоящему моменту времени методы последовательной дискретизации базируются на разбиении области определения, в первую очередь, по пространственным переменным, сводя исходную начально-краевую задачу к системе обыкновенных дифференциальных уравнений по времени (метод прямых), для интегрирования которой употребляются как явные [9–11], так и неявные разностные схемы [5, 12–16 и другие], в том числе основанные и на методах Рунге–Кутты [5, 11, 12, 15, 16 и другие].

Особенность применения обобщенных МРК заключается в том, что при последовательной дискретизации область определения решения динамической задачи сначала разбивается по времени, а уж затем (если потребуется) — по пространственным переменным. В ряде случаев такой подход более целесообразен, так как уравнения движения, как правило, содержат дифференциальные операторы по пространственным переменным сложной (часто нелинейной) структуры и достаточно простые дифференциальные операторы по времени [9, 14 и другие]. Указанная последовательность дискретизации начально-краевых задач динамики позволяет в каждый дискретный момент времени поступать более гибко, а именно прибегать к разнообразным методам интегрирования по пространственным переменным, разработанным для решения задач статики [6, 7, 17 и другие].

Известно, что уравнения газовой динамики вытекают из законов сохранения, поэтому, будучи записанными в дифференциальном виде, они имеют дивергентную форму [1, 18 и другие]. Простейшим же уравнением с частными производными, имеющим дивергентную форму, является уравнение переноса [1, 19]. Кроме того, приложение метода Даламбера (метода бегущих волн) к интегрированию одномерного волнового уравнения в акустическом приближении приводит к представлению решения в виде суммы двух функций, описывающих прямую и обратную бегущую волны [2 и другие]. Каждая из этих функций удовлетворяет соответствующему уравнению переноса. В силу этого уравнение переноса является модельным и делает возможной «отработку» схемы для более сложных уравнений акустики, нелинейных уравнений газовой динамики и других [1, 19]. А значит, исследование численных схем интегрирования этого уравнения обобщенными МРК представляет методологический интерес.

В работах [6, 7] показано, что некоторые классические конечно-разностные схемы интегрирования уравнения переноса могут быть получены как следствие применения обобщенных МРК. Изучению спектральной устойчивости этих неклассических методов при численном интегрировании начальной задачи для уравнения переноса и посвящена настоящая статья.

• 2.    Некоторые предварительные замечания

Рассмотрим задачу Коши для уравнения переноса ly = ady, y(0, x) = yо (x), |x| <*, t >0, a = ±1,(1)

и t где y0 (x) — дифференцируемая функция. Решением задачи (1) является «бегущая волна» [1, 19]:

y (t, x ) = y0 (x + at).(2)

Дискретизируем начальную задачу (1) по времени, то есть будем рассматривать ее решение в моменты времени tn+1 = tn +T (n = 0,1,2,...), t о = 0,(3)

где т — шаг по времени (возможно, переменный: т = т _{n + 1}).

Далее исследуем спектральную устойчивость приближенных решений начальной задачи (1), полученных разными обобщенными МРК в дискретные моменты времени (3). Для этого по аналогии с [1, 19] представим решение при t = tn в виде гармоники yn (x ) = y (tn, x ) = qn sin (kx + ф n) (n = 0,1,2,...).(4)

Тогда в следующий момент времени решение, в силу свойства «бегущей волны» (2), должно иметь вид yn+1 (x ) = qn+isin (kx+ Ф n+i),     |x| <*>     Ф n+i = Ф n + 6 n, где k, qn, qn+1, фn, 6n — некоторые постоянные, причем qn+1, 9n зависят от а, k, qn, фn, т. Здесь 6n — сдвиг фазы гармоники, характеризующий свойство переноса («бегущую волну»).

Введем норму решения в пространстве С :

IIynlL=maxyn(x)l (n=0,1,2,...), откуда и из (4), (5) имеем

||Л L = kJ,    |y-*1 = q-+11-(7)

Отношение

R = R (а, т, к) = qn+1|/qn| > 0, по аналогии с терминологией, принятой в [5], целесообразно назвать функцией спектральной устойчивости соответствующего обобщенного МРК при его приложении к начальной задаче для уравнения переноса (1). Согласно (6)-(8) при R > 1 обобщенный МРК спектрально неустойчив; если же R < 1, то метод спектрально устойчив, причем при

R = 1(9)

он не обладает свойством асимптотической устойчивости, а при

0 < R < 1(10)

обобщенный МРК асимптотически устойчив (то есть любые возмущения начального коэффициента q ₀ с увеличением номера момента времени n затухают).

В силу равенств (4), (5), (8) для определения функции устойчивости достаточно в (4) принять qn = 1,(11)

тогда из (8) последует

R ( а , т , k ) = q n +1 ( а , т , к )| >  0.

Таким образом, чтобы установить функцию устойчивости R какого-либо обобщенного МРК, необходимо знать коэффициент qn+1 в (5) при выполнении равенств (4), (11). Продемонстрируем это на примере некоторых конкретных обобщенных МРК.

Для решения задачи Коши (1) наиболее естественным является использование явных схем [1, 19]. Поэтому сначала для численного интегрирования начальной задачи (1) обобщенными МРК, как и в [6, 7], прибегнем к явному методу Эйлера и найдем выражение

y^{n + 1 (} x ) = y^{n (} x ) ' ^тд у

, откуда с учетом

следует yn+1 (x) = yn (x) + ат(yn (x)) ,                                         (13)

где штрих означает производную по x .

Подставим в (13) выражение (4) с учетом (11), тогда после элементарных тригонометрических преобразований, согласно (5), получим yn+1 (x) = sin (kx + ф n ) + ат k cos (kx + ф n) = qn+1 sin (kx + ф n+1),                     (14)

где

Q n +i = V ^{1 +}(^{T k} ) ² ,  ф n +i = ф n ^{+ 9} n ,   ^{cos 9} n = V q n +i ,  ^{sin 9} n = ^ат kq n +i .                    ⁽¹⁵⁾

Из (14), (15), (8) следует, что при a = ± 1, т> 0 и k >  0 (то есть при т k >  0) имеет место неравенство R ( т k ) > 1, а значит обобщенный явный метод Эйлера применительно к (1) не обладает спектральной устойчивостью.

Если аппроксимировать производную в (13) конечными разностями на разных шаблонах, то придем к некоторым общеизвестным явным конечно-разностным схемам. Так, используя правые и левые разности, будем иметь yn+1 = yn +0^ y;+1 - yn);(16)

A yn+1=yn+a.T( yn—ynA),(17)

где yn = y (t„, x;), x;+1 = x;+A (; = 0, ± 1, ± 2,..., x0 = 0);(18)

A — шаг по пространственной переменной x (возможно, переменный: A = A _; ).

Схема (16) условно устойчива в пространстве С сеточных функций y n при a = 1, т/ A <  1, а схема (17) условно устойчива при a = - 1, т/A< 1; в остальных случаях эти схемы неустойчивы [1, 19]. Отметим, что явный метод Эйлера для интегрирования начально-краевой задачи по времени нашел применение, например, в работе [11].

Аппроксимируя производную в (13) с помощью центральной разности, получим явную схему yn+1=yn+0Т( y;+1 - y-1).

Известно, что схема (19) неустойчива при a = ± 1 и любых т/A [1, 19].

Исследуем спектральную устойчивость некоторых неявных обобщенных МРК применительно к численному интегрированию начальной задачи (1). Сначала возьмем коэффициенты одностадийного метода Радо IIA (далее, как и в [6, 7], для краткости будем говорить: «воспользуемся таким-то методом» по аналогии с терминологией, принятой в [5], и использовать коэффициенты соответствующей этому методу матрицы Бутчера) — неявного метода Эйлера, тогда получим y n ⁺¹ ( x ) = y n ( x ) + та У 1 ' ( x ) ,

Y1 (x) = yn (x) + таY'(x) (здесь и далее Ym (x) — некоторые вспомогательные функции [6, 7]), откуда ат(yn+1 (x))'- yn+1 (x) = -yn (x).                                               (20)

Подставляя в правую часть (20) выражение (4), учитывая (11) и разыскивая решение в виде (5), на основании (12) найдем

R ( т k ) =

V1+(т k )2

cos 9 _n

1 X ²

R X ² + k ²’

sin 9 n

X k

R X ² + k ² ,

X = ⁰ .

т

Из (21) следует, что при а = ± 1, т k >  0 выполняются неравенства (10), то есть одностадийный метод Радо IIA применительно к (1), в отличие от (13), обладает асимптотической спектральной устойчивостью. Отметим, что к соотношениям (21) приводит и одностадийный метод Радо IA.

Аппроксимируя производную в (20) правыми или левыми конечными разностями, получим общеизвестные неявные конечно-разностные схемы на трехточечных шаблонах (см. (18))

0т ( y n++11 - y n ^{+ 1} ) - y n ^{+ 1} =- y n ; A ^v            '

^у " ^{+ 1} - y^ ) — у " ^{+ 1} =— у " .

Известно, что схема (22) безусловно устойчива в пространстве С сеточных функций у " при а = - 1, а схема (23) — при а = 1 [1, 7, 19].

Рассмотренные выше одностадийные обобщенные МРК имеют первый порядок точности по т . Далее исследуем спектральную устойчивость обобщенных МРК более высоких порядков точности по т .

Проинтегрируем задачу (1) с помощью одностадийного метода Гаусса–Лежандра (метода средней точки, имеющего второй порядок точности по т): у"+1 (x) = у" (x) + таY1'(x), Y1(x) = у" (x) + 0,5таY'(x). В результате найдем у"+1 (x) = 2Y1 (x)-у" (x),     Y’(x) = ^(Y1 (x)-y" (x))                           (24)

или y"+1 (x) = y" (x) + аТ[(У"+1 (x))'+(y" (x))'].                                       (25)

К уравнениям (24) приводит и использование двухстадийного метода Лобатто IIIB, а соотношение (25) является известной формулой трапеций, соответствующей двухстадийному методу Лобатто IIIA [5], поэтому дальнейшие рассуждения справедливы и для этих методов.

Подставим в (25) выражения (4), (5) с учетом (11), тогда на основании (12) после элементарных тригонометрических преобразований получим

_ .               X ² - к²       .         2X к

.   2а

X = —.

т

R "  1,    cos ° "   л ^; - / л , sin ° " ⁼ X 2 + k

Так как для функции устойчивости R выполняется тождество (9), то одностадийный метод Гаусса–Лежандра и двухстадийные методы Лобатто IIIA и IIIB применительно к начальной задаче (1) спектрально устойчивы, но не обладают свойством асимптотической устойчивости.

Замечание 1. Формулы (15), (21), (26) показывают, что всем рассмотренным выше обобщенным МРК при фиксированных а и т присуще свойство зависимости сдвига фазы гармоники 9 n от ее частоты к . Согласно точному решению (2), этого не должно быть. Зависимость 9 n от к становится исчезающе малой при т ^ 0 .

Если для интегрирования второго уравнения (24) (или, что то же самое, для уравнения (25)) прибегнуть к двухстадийному методу Лобатто IIIA (методу трапеций [5]), то из (24) последует

Y+1 =   '   [(1 + аH) Y - аH (у" + y"^)],    y^1 = 2Y - у^;(27)

1 -а HLv

Yi = —Ц:[(1 -аH)Y+1 +аH(у" + y"^)],  yn+1 = 2Y^ -yn,(28)

1 + а HLv где Y^ = Y (xi ), H = А/т. За счет первых соотношений исключим из вторых равенств (27), (28) величины

Y

Y i и в образовавшихся уравнениях заменим Y 1i , Y 1i ^{+ 1}

выражениями

Y i = 2 ( y " ^{+ 1} + y " ) ,

yi +1

Y ₁

= ^( Ум + y "_{+ 1} ) , которые следуют из первого равенства (24).

В итоге придем к классическим

конечно-разностным схемам второго порядка по обеим переменным, построенным на четырехточечном шаблоне [1, 19]:

у " ⁺ 1 = ay- n ^{+ 1} + y n - ay n_v a = ( 1 + а H )/( 1 -а H ) , а = - 1;                      (29)

У " ⁺ 1 = by^ + У "+1 — by " , b = ( 1 -а H )/( 1 + а H ) , а = 1.                      (30)

Известно, что схемы (29), (30) абсолютно устойчивы в энергетической норме [1, 19] (то есть в некотором интегральном смысле). Однако, как показано в [7], эти схемы неустойчивы в норме пространства С сеточных функций у". Единственным исключением является случай H = 1, когда т = А, a = b = 0 . При этом из (29), (30) следует равенство переноса у"+ = у" при а = -1 и у"+1 = у”+1 при а = 1.

Таким образом, проведенные предварительные исследования показывают, что явные обобщенные МРК, будучи примененными к интегрированию начальной задачи (1), обладают, по-видимому, спектральной неустойчивостью, и следствием этого является неустойчивость или условная устойчивость конечно-разностных схем, построенных на их основе после дискретизации задачи по пространственной переменной x (см. (18)). Неявные же обобщенные МРК можно разделить на две группы. К первой группе относятся спектрально устойчивые методы (функция устойчивости имеет вид (9)), но не обладающие свойством асимптотической устойчивости. Конечно-разностные схемы, построенные на базе таких методов, могут оказаться неустойчивыми в пространстве С сеточных функций у " , хотя при этом могут быть и устойчивыми в некоторой энергетической норме (см. (29), (30)). Ко второй группе относятся методы, спектрально и асимптотически устойчивые, для которых функция устойчивости обладает свойством (10). Есть основания предполагать, что конечно-разностные схемы, построенные на базе последних методов, будут обладать безусловной устойчивостью (см. (22), (23)), хотя окончательно этот вопрос для всех таких методов пока еще не решен.

• 3.    Общий алгоритм исследования спектральной устойчивости обобщенных МРКпри применении их к начальной задаче для уравнения переноса

Согласно [6, 7] использование s -стадийного обобщенного МРК для интегрирования начальной задачи (1) приводит к системе обыкновенных дифференциальных уравнений по пространственной переменной x следующего вида:

y (x) = у" (x)e + атAy'(x);(31)

у"+1 (x) = у" (x) + атb*y'(x),(32)

где y (x ) = {Y( x), Y2 (x),..., Ys( x)} , b = { b1, b2,..., bs }*, e = {1,1,..., 1}*;(33)

y ( x ) — s -компонентная вспомогательная вектор-функция; A = ( a ij ) — s x s -матрица Бутчера соответствующего МРК; b — s -компонентный вектор-столбец, составленный из элементов последней строки матрицы Бутчера (см. соотношение (3.1.6) в [5]); e — s -компонентный вектор-столбец, все элементы которого равны единице; звездочка означает операцию транспонирования.

Замечание 2. Без потери общности рассуждений для упрощения выкладок в (4) можно принять ф n = 0 и учесть (11), тогда из (5), (12) получим функцию устойчивости и ф n _{+ 1} = 9 n .

Подставим (4) в (31), что позволит разыскивать периодическое по x решение системы (31)

y ( x ) = u sin kx + v cos kx ,    |x | <« ,

где u , v — s -компонентные векторы-столбцы, подлежащие определению. Из системы (31) с учетом (4), (34) и Замечания 2 следует матричное равенство u sin kx + v cos kx = e sin kx + атA (u k cos kx - vk sin kx).

Так как функции sin kx , cos kx являются линейно независимыми, то из (35) вытекают матричные соотношения

• u = e - ат k Av ;

  
  

v = ат k Au .                                           (37)

Подставив (37) в (36), найдем матричное уравнение u = e - ( ат k ) 2 A ² u , откуда

[ l + ( т k ) 2 A ² J u = e ,

где I — единичная 5 х 5 -матрица. Матричное уравнение (38) представляет собой систему линейных алгебраических уравнений относительно компонент вектора-столбца u . Решив это уравнение, определим вектор-столбец u , после подстановки которого в (37) получим и вектор-столбец v .

Согласно (5) имеет место разложение y ” ^{+ 1} ( x ) = y " ^{+ 1} sin kx + y _c ” ^{+ 1} cos kx , где y _s ” ^{+ 1} , y _c ” ^{+ 1} — разыскиваемые коэффициенты. Учет этого выражения в (32), а также (4), (34) и Замечания 2 дает выражение:

ySC+1 sin kx + y”+1 cos kx = sin kx + атЬ* (uk cos kx - vk sin kx), из которого следует yC+1 = 1 -ат kb* v,      y”+1 = ат kb*u.                                   (39)

В соответствии с (5), (11), (12) и Замечанием 2, из (39) окончательно найдем

R ( а , т k ) = / y C ^{+ 1} ) 2 + ( y ” ^{+ 1} ) 2 , cos 0 „ = y ” ^{+ 1} R , sin 0 „ = y ” ^{+ 1} / R .                   (40)

На основании соотношений (37)–(40) можно исследовать спектральную устойчивость обобщенных МРК разных порядков точности. Для этого необходимо использовать лишь компоненты матрицы Бутчера должного МРК [5]. В случаях малостадийных МРК (низких порядков точности) функцию устойчивости R можно получить в явном виде (что и было проделано в разделе 2). В случаях же многостадийных МРК (высоких порядков точности по т ) целесообразно изучать функцию устойчивости по схеме (37)-(40) численно, варьируя произведение т k от нуля до бесконечности (машинной бесконечности). Далее рассмотрим спектральную устойчивость конкретных обобщенных МРК разных порядков точности.

Ненулевые компоненты матрицы Бутчера явных МРК расположены под главной диагональю [7, 20], поэтому компоненты Y m ( x ) (1 <  m <  5 ) вектора y ( x ) (см. (33)) вычисляются последовательно из уравнений системы (31) без интегрирования ее по переменной x (что и характеризует подобные методы как явные). При этом структура решения системы (31) с учетом (4) имеет вид (34), и поэтому рассуждения (35)–(40) остаются в силе. Исследование явных обобщенных МРК, компоненты матриц Бутчера которых приведены в [20], показало, что все они, как и (13), спектрально неустойчивы.

В случае применения неявных обобщенных МРК требуется интегрирование по переменной x системы (31) относительно вектор-функции y ( x ) . Прямые вычисления, проведенные для всех обсуждаемых ниже неявных обобщенных МРК, показали, что собственные числа системы (31) не являются чисто мнимыми, то есть общие решения однородной системы (31) (при y ” ( x ) = 0) не обладают свойством периодичности. Поэтому при задании y ” ( x ) в виде (4) и требовании периодичности решения по x для функции y ” ^{+ 1} ( x ) (в силу свойства «бегущей волны») получается, что произвольные постоянные, возникающие при интегрировании системы (31), необходимо принять равными нулю, и вследствие этого равенства (5), (34) и весь алгоритм изучения спектральной устойчивости соответствующего обобщенного МРК (см. (35)–(40)) остаются справедливыми.

• 3.1.    Неявные обобщенные МРК, не обладающие свойством

асимптотической спектральной устойчивости

Как уже отмечалось, для этих методов справедливо тождество (9). Проведенные исследования показали, что все обобщенные методы Гаусса–Лежандра, Лобатто IIIA и IIIB удовлетворяют равенству (9). В случае применения этих методов второго порядка точности по т , как продемонстрировано выше, выполняются соотношения (26). Для двухстадийного метода Гаусса–Лежандра и трехстадийных методов Лобатто IIIA и IIIB (с четвертым порядком точности по т ) по схеме (31)-(40) справедливы следующие равенства:

R = 1, sin 0 ”

12 атX ( 12 -X ² ) 144 + 12 Х ² + X ⁴ ’

cos 0 ”

72 X 2

144 + 12 X 2 +X 4 ,

X = т k .

Для трехстадийного метода Гаусса–Лежандра и четырехстадийных методов Лобатто IIIA и IIIB (с шестым порядком точности по т ) выражения для R , 0 _C не были построены аналитически в силу громоздкости выражений компонент их матриц Бутчера через иррациональные дроби [5]. Непосредственные вычисления по формулам (31)–(40) показали, что для этих методов также имеет место тождество (9).

• 3.2.    Неявные обобщенные МРК, обладающие свойством

асимптотической спектральной устойчивости

В настоящем разделе рассматриваются обобщенные МРК, для которых выполняются условия (10) при т к >  0 . Проведенные исследования продемонстрировали, что этим свойством обладают все методы Радо IA и IIA, а также методы Лобатто IIIC. Для одностадийных методов Радо (первый порядок точности по т ) выше были получены равенства (21).

Применение обобщенных МРК приводит к следующим соотношениям:

• -    двухстадийный метод Радо IA (третий порядок точности по т )

  r ( х_Н  3-4 - ,

  ^v     N 36 + 4 X ² + X ⁴

  36 - 6 X ²

  
  

  0„ = ®„ + V„,   sin V„

  n nn ,      n

  
  

  24 aX

  
  

  А ( Х ) ( 3б + 4 X ² + X ⁴ ) ’

  
  

  cos V n

  
  

  А ( Х ) ( 3б + 4 X 2 + X ⁴ ) ’

  
  

  A ( X ) = J -----³⁶---г,  sin ®„

  ^v ’ У 36 + 4 X ² + X ^{4 n}

  
  

  aX

  3 5 ( X ) ’

  
  
  
  

n 1               /9 + X2    1 t cos0n = w, 5(XW _v, X=тk;

o ( X )              V 9

• -    двухстадийный метод Радо IIA (третий порядок точности по т )

  sin 0 n

  
  

  ^R (^X) = ^ 2 aX ( 18 -X² )

  
  

  1296 + 288 X 2 + 52 X ⁴ + 4 X 6

  1296 + 288 X 2 + 88 X 4 + 8 X 6 + X ⁸ ,

  
  

  R ( Х ) ( 3б + 4 X ² + X ⁴ ) ’

  
  

  _A        36 - 14 X 2

  cos 0„ =-------7---------:----- tv ,

  n    R ( X ) ( 36 + 4 X ² + X ⁴ )

  
  

  X = т к ;

  
  
  
  

  - двухстадийный метод Лобатто IIIC (второй порядок точности по т )

R (X) =

4 + X ⁴ ,

sin 0» = "T™Г,   cos 0»

n    R ( X ) ( 4 + X ⁴ ) ,          n

4 - 2 X 2

R ( X ) ( 4 + X ⁴ ) ’

X = т к ;

- трехстадийный метод Лобатто IIIC (четвертый порядок точности по т )

_{R M}=     331776 + 41472 X 2 + 1296 X ⁴ + 576 X ⁶ + 36 X 8

¹¹ У 331776 + 41472 X 2 + 1296 X ⁴ + 1152 X ⁶ + 72 X 8 + X ¹² ’ . ₀ =     1 ^{2 aX} ( ^{48 -} 5 ^{X 2} )           ₀ = 576 - 252 X ² + 6 X ⁴

X = т к .

s™ n    R ( X ) ( 576 + 36 X ² + X ⁶ ) ’ cos n R ( X ) ( 576 + 36 X 2 + X ⁶ ) ’

Функции устойчивости, вычисленные по формулам (21), (42)-(45) при т к е ( 0, да ) , монотонно убывают от 1 (при т к ^ + 0) до 0 при т к ^ да .

Для трехстадийных методов Радо IA и IIA (пятый порядок точности по т ), а также для четырехстадийного метода Лобатто IIIC (шестой порядок точности по τ) аналитические выражения для R , 0 _n не были получены в силу громоздкости выражений компонент их матриц Бутчера через иррациональные дроби [5]. Непосредственные вычисления по формулам (31)–(40) показали, что функция устойчивости R этих методов также монотонно убывает от 1 до 0 при т к е ( 0, да ) .

• 3.3.    Диагонально неявные обобщенные МРК

Среди неявных обобщенных МРК особое место занимают диагональные методы, так как для них ненулевые компоненты матрицы A (см. (31)) расположены на главной диагонали и под ней, что позволяет интегрировать уравнения системы (31) последовательно на каждой стадии используемого многостадийного метода. Так, например, двухстадийный диагонально неявный метод (метод Нёрсетта) характеризуется следующими ненулевыми компонентами матрицы A и вектора-столбца b :

^ti ii = a 22 = У ,    a 21 = 1 - 2 у ,    b = b 2 = 1/2,

где у — некоторая постоянная. При у = 0,5 + V3/6 достигаем при определении величин y n ^{+ 1} точности третьего порядка по т , при остальных значениях у — второго [5]. На основании соотношений (31)-(40), с учетом (46), имеют место равенства

R (x) =

wp ■ л ^; ) ■ |ф л ^; ) 2_Хи ■ x ^; ) ' ■ 4 л ^; |р zU ■ x ^; ) | 2 2 у ² ( 1 + x ² ) ²

^x[ p-x^{( 1 +x} 2 ) ]            _v ( i ^{+x 2} ) ² +3 ( 1 ^-x 2 ) - 2 x ( 1 ^+x 2 )

Уn = ----------------Г, cos У n =--------------------------i--------- у2 R (x)(1 + x2)                         2у2 R (x)(1 + x2)

^ = 1 - 4 y + 2 y ² , p = 1 - 2 y , x = 1 - 3 y , x = аут к .

Расчеты показали, что согласно (47) функция устойчивости R ( x ) при 0 < |x| < го (или, что то же самое,

при 0 < т к < го ) монотонно изменяется от 1 до значения

R = lim R (x)= 1 + 1-4^ ” |x| m ⁽ )          2 у ²

откуда следует, что при у> 0,5 выполняются неравенства R _го< 1, R _го< R ( x ) <  1 (то есть справедливы неравенства (10)). В частности, при у = 0,5 + V3/6 >  0,5 получаем R _го = 0,7321 и третий порядок точности по т , а при у< 0,5 из (49) имеем R _го> 1, то есть в последнем случае метод Нёрсетта спектрально неустойчив.

Трехстадийный диагонально неявный метод (метод Барриджа) характеризуется следующими ненулевыми компонентами матрицы A и вектора-столбца b :

ая=у (i = 1,3), a 21 = 0,5-у, a 31 = 2у, a 32 = 1 - 4у, b = b3 = [24 (0,5 -у)2 ]"', b2 = 1 - [12 (0,5 -у)2 ]"', где у — по-прежнему некоторая постоянная. При

у = — + -

метод имеет четвертый порядок точности, а при других у — третий [5]. Численный анализ, проведенный по формулам (31)–(40) с учетом (50), (51), показал, что для метода Барриджа функция устойчивости монотонно убывает от 1 до 0,6304 при т к е ( 0, го ) . Следовательно, оба диагональных обобщенных МРК (метод Нёрсетта при у = 0,5 + V3/6 и метод Барриджа при выполнении равенства (51)) обладают свойством асимптотической спектральной устойчивости.

Для всех неявных обобщенных МРК после дискретизации задачи (1) по времени t получается система обыкновенных дифференциальных уравнений по пространственной переменной x (см. (31)). В случае решения начально-краевой задачи для уравнения переноса (когда на полуоси t = 0, x е [0, го) или t = 0, x е(-го, 0] задано начальное условие, как в (1), а на полуоси x = 0, t е [0, го) — некоторое краевое условие для функции y (t, x) [1, 19]) проинтегрировать эту систему уравнений численно можно с применением обычных МРК [5]. При этом краевое условие при x = 0, t е [0, го) выступает в качестве «начального» условия по переменной x . Если же рассматривается начальная задача (1) с периодической функцией y0 (x), то согласно (2) в каждый дискретный момент времени tn решение будет периодическим по x . В этом случае система (31) может быть также проинтегрирована обычными МРК, для чего в некоторой точке x (например x = 0) «начальные параметры» для однозначного интегрирования возникающей при такой постановке задачи Коши должны быть определены из условия периодичности решения по x . С этой целью можно использовать, например, метод пристрелки (как это сделано в [7]). После такой последовательной дискретизации начальной или начально-краевой задачи для уравнения переноса по обеим переменным t и x будем иметь нужные конечно-разностные схемы численного интегрирования (именно таким путем классические схемы (22), (23) и (29), (30) найдены из дифференциальных уравнений (20) и (25) соответственно, причем эти схемы рекомендованы для численного интегрирования именно начально-краевых задач для уравнения переноса [1, 19]). При этом совершенно не обязательно для дискретизации системы (31) по переменной x использовать те же МРК, что и употребленные для дискретизации задачи (1) по времени t . Эта возможность существенно расширяет семейство конечно-разностных схем, которые можно построить на базе МРК для численного интегрирования начально-краевой задачи для уравнения переноса. Изучение устойчивости таких схем является самостоятельной проблемой вычислительной математики, которая выходит за рамки настоящей работы.

Проведенное выше исследование относится к одному одномерному по пространственной переменной уравнению с частными производными первого порядка [1, 19]. Однако результаты могут быть обобщены и на многомерный пространственный случай. При этом под x и k нужно понимать векторы-столбцы соответствующих евклидовых пространств размерности r ( r = 1, 2, 3), а под произведением kx (см. (4) и далее) — скалярное произведение этих векторов . Кроме того, известно, что все схемы методов Рунге–Кутты, полученные для одного уравнения, полностью переносятся и на системы уравнений [5-7, 20], то есть на случай, когда в (1) под у , у ₀ понимаются вектор-функции, а под а — квадратная матрица той же размерности, что и у , у ₀ (предполагается, что жорданова форма матрицы а является диагональной, поскольку это обеспечивает гиперболичность системы (1) [18]). Однако, несмотря на элементарность такого переноса схем Рунге–Кутты на системы уравнений, открытым пока остается вопрос об адекватном выборе требуемой функции устойчивости R , которая в случае одного уравнения определяется достаточно просто (см. (8)).

• 4.    Обсуждение результатов расчетов для уравнения переноса

Для апробации полученных выше схем интегрирования начальной задачи (1) рассмотрим случай а = - 1 при начальном условии

M 8

у 0 ( x ) = ^ , s^m ( k m X ) , k m = 2 п ( 2 m - 1 ) ( M = 1,2,3,...),                    (52)

m =1 km которое представляет собой конечную сумму гармоник. Сравнивая (52) и (4) при n = 0 , находим q0m) = 8/km, ф0m) = 0, 1 < m < M.                                   (53)

Согласно (52) функция у ₀ ( x ) является частичной суммой ряда Фурье для периодической ступенчатой функции

- 1, - V ² + ¹ <  x <  ¹ ;

• ^{2 (} x )    { + 1, 1 <  x <  1/2 + 1 ( 1 = 0, ± 1, ± 2,...)

  
  
  
  

с периодом X = 1. Точное решение начальной задачи Коши (1), (52) в силу (2) имеет вид

M 8

у ( t , x ) = Е ,s^ln ( k m ( x - t ) ) . m =1 k m

Из равенства (55) следует, что на прямых x - 1 = 1 /2 частные производные по модулю составляют

5 у

5 t

д ^у = 8 ^ cos ( п ( 2 m - 1 ) 1 ) = 8 M ,

M

m =1

а модуль градиента решения в этих точках равен 82M . Стало быть, с увеличением числа гармоник модуль градиента возрастает, и уже при M = 5 его можно считать большим по сравнению со значениями модуля функции (55). Кроме того, из теории рядов Фурье известно, что в окрестности точки разрыва функции (54) ее разложение (52) имеет неустранимые «пики» (проявляется эффект Гиббса), и чем больше значение M , тем больше вторые производные от у0 (x) в точках, соответствующих этим пикам. А значит, решение рассматриваемой начальной задачи (1), (52) при больших M обладает не только большими по модулю производными первого порядка (56), но и большими по модулю производными высших порядков (вследствие локальных эффектов).

В качестве конкретного примера рассмотрим случай M = 30 . При этом максимальные значения модуля градиента решения превышают 330, а модуль функции (55) с учетом эффекта Гиббса не превосходит значения 1,18, то есть градиенты решения являются большими и периодически повторяющимися. Именно на задачах с такими особенностями решения целесообразно апробировать обобщенные МРК (особенно высоких порядком точности). С наибольшей полнотой удается выяснить достоинства и недостатки этих методов, трудно оцениваемых на весьма гладких (типа одной гармоники) решениях начальной задачи (1). Отметим, что качественно подобные ситуации (по крайней мере для скоростей точек среды) при отыскании решения в виде бегущей волны ступенчатой формы (или близкой к ней) возникают при исследовании механического поведения сплошных сред, подвергнутых ударному воздействию [1, 2, 16].

Согласно (4), (5), (52), (53) в момент времени t _n все анализированные выше обобщенные МРК дают решение рассматриваемой начальной задачи в виде

M yn (x) = £qnm)sin(kmX + ^nm)) (n = 0,1,2,...).(57)

m =1

Учитывая (6), (7), оценим норму решения (57) в пространстве С :

MM

IIynlс=maxIynl < £qnm1■ lsin(kmx+^nm))l < £qnm)I • m=1

На основании (8), (58) при постоянном по времени шаге т получаем

MM

I ynl с<£ qm )| = £[ R (т km)] nq 0 m )| - SM   (n = 0,1,2,...),(59)

m =1

где q 0 ^m ) имеют значения (53). Заметим, что в расчетах шаг т выбирался так, чтобы 10 шагов по времени были равны периоду колебаний высшей гармоники в решении (55), то есть при m = M .

Если обобщенный МРК не обладает асимптотической спектральной устойчивостью, то из (59) с учетом (9) следует

M

I y n l _с< sM - £ q 0 ^m ) , ( n = 0,1,2,...).                                   (60)

m =1

Из (60) видно, что норма решения при n ^ от остается ограниченной сверху числом S M , то есть метод является устойчивым, но в силу Замечания 1 приближенное решение (57) при этом может существенно отличаться от точного решения (55). Так, при M = 30 из (60) найдем || yⁿ ||< 3,415, а норма точного решения составляет || у ||® 1,179 (этот факт продемонстрирован ниже на конкретном примере). Вследствие (52), (53), (60) при M ^от имеем lim S M ^от , то есть с увеличением числа слагаемых в разложении (52) (с увеличением градиентов решения (56)) возрастает вероятность все более существенного расхождения точного и численного решений (вплоть до полной потери точности).

Если же обобщенный МРК обладает свойством асимптотической спектральной устойчивости, то из (59) с учетом (10), (60) вытекает неравенство

I yⁿ ||_с< S M <  S M ( n = 0,1,2,...),

причем limSM ^ 0 (наблюдается асимптотическая устойчивость). Значит, подобные МРК дают разность n ^от точного и приближенного решений при достаточно больших n в худшем случае того же порядка, что и норма точного решения. По-видимому, именно таким обобщенным МРК стоит отдавать предпочтение. Продемонстрируем это на примере конкретных расчетов.

Так как точное решение (55) является периодическим с периодом T = X = 1 (равным периоду колебаний низшей гармоники при m = 1, см. (52)), то внутри каждого периода колебаний целесообразно ввести локальное время t* (0 < t*< T = 1). Тогда глобальное t и локальное t* времена будут связаны между собой соотношением t = t .+ TN = t .+ N, 0 < t *< 1 (N = 0,1,2,...), (62)

где N — количество периодов колебаний низшей гармоники, предшествующих рассматриваемому периоду.

На рисунках 1–4 приведены точные (кривые 1 ) и приближенные (остальные кривые) решения начальной задачи (1), (52) в точке x = 0 при малых, средних и больших значениях времени t . Согласно (62) на рисунках по оси абсцисс отложено локальное время t * и для каждого из рисунков указано свое значение N : N = 0 для рисунка 1 а (окрестность начального момента времени t = 0 ); N = 50 для рисунков 2 а -4 а (средние значения времени t ); N = 5 - 10 ⁴ для рисунка 1 б , рисунков 2 б-г , рисунка 3 б и рисунка 4 б (большие значения времени t ).

На рисунке 1 изображены приближенные решения начальной задачи (1), (52), полученные на базе обобщенных МРК низких порядков точности: кривые 2 рассчитаны одностадийным методом Гаусса-Лежандра (методом средней точки, имеющим второй порядок точности по т ), а также двухстадийными методами Лобатто IIIA и IIIB по формулам (24)–(26), кривые 3 определены на основе двухстадийного метода Лобатто IIIC (второй порядок точности по т ; см. (44)), а кривые 4 — на основе одностадийных методов Радо IA и IIA (неявного метода Эйлера, имеющего первый порядок точности по т ; см. (20), (21)).

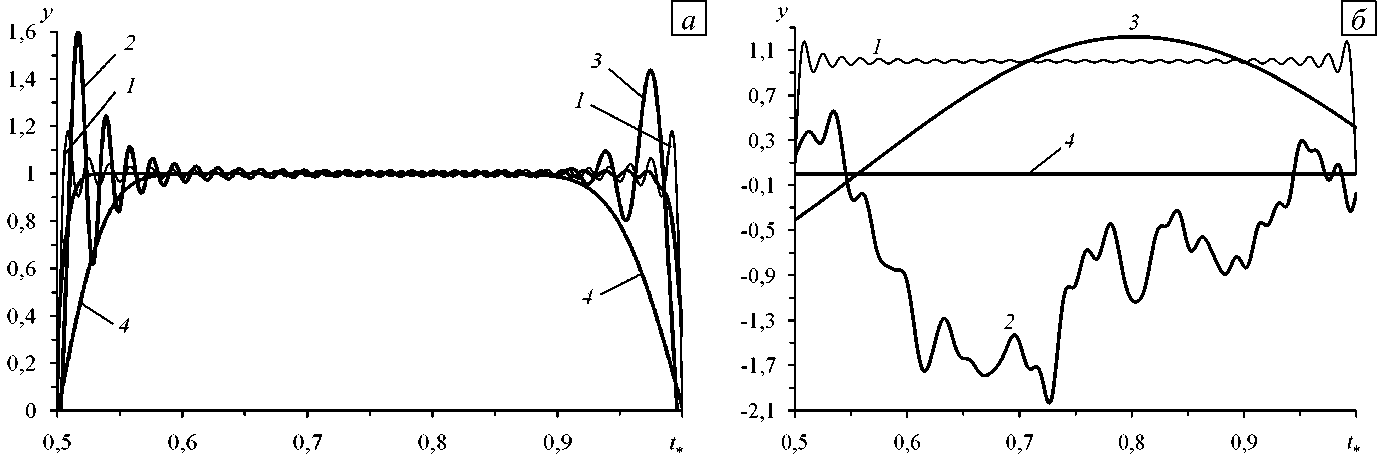
Рис. 1. Характер решений (кривые 2 – 4 ) на основе обобщенных МРК низких порядков точности при различных значениях времени: при малых ( N = 0 , см. (62)) временах ( а ), при больших ( N = 5 - 10⁴) временах ( б ); 1 - точные решения; 2 – одностадийный метод Гаусса–Лежандра и двухстадийные методы Лобатто IIIA и IIIB (второй порядок);

3 – двухстадийный метод Лобатто IIIC (второй порядок); 4 – одностадийные методы Радо (первый порядок)

Судя по характеру кривых 2 , 3 на рисунке 1 а , уже на начальном участке времени ( N = 0, см. (62)) метод средней точки и двухстадийные методы Лобатто дают решения с резким увеличением «пиковых» значений (экстремумов) в окрестности точек t , « 0,5 и t * « 1 соответственно (то есть в окрестности точек, в которых точное решение (55) имеет большие по модулю градиенты (56)). Поведение же кривых 2 , 3 на рисунке 1 б показывает, что согласно проведенному выше анализу (см. (58)–(60)) при больших значениях времени t метод средней точки и методы Лобатто IIIA и IIIB приводят к полной потере точности (см. кривые 1 и 2 на рисунке 1 б ), а метод Лобатто IIIC отслеживает решение лишь в некотором «общем смысле». Последнее объясняется тем, что в силу (44), (57), (59) все высшие гармоники при таких больших значениях t практически уже затухают, и приближенное решение, по сути, определяется лишь низшей гармоникой ( m = 0), амплитуда которой также со временем уменьшается, поэтому кривая 3 на рисунке 1 б уже не несет локальных эффектов, присущих точному решению (см. кривую 1 ).

Отметим, что аналогично кривой 2 на рисунке 1 а ведет себя и численное решение (см. кривую 4 на рисунке 2 в [7]), полученное при H ^ 1 по схеме (29), которая, как показано в [7], неустойчива в норме пространства С сеточных функций у*П .

Кривая 4 на рисунке 1 а показывает, что решение неявным методом Эйлера (см. (20)) уже на начальном этапе отражает только общую (в некотором осредненном смысле) тенденцию поведения решения задачи

(1), (52), но не передает локальных особенностей точного решения (55), в частности, не выделяет локальных экстремумов. Это вызвано быстрым затуханием высших гармоник в разложении (57) при выбранном шаге по времени τ . С увеличением времени t , согласно (21), (57), (61), приближенное решение достаточно быстро затухает, поэтому на рисунке 1 б линия 4 визуально не отличается от горизонтальной прямой y = 0 (значения yⁿ имеют порядок 10 ^{- 8} ). Отметим, что с кривой 4 на рисунке 1 схож вид кривой численного решения, полученного по схеме (22) при τ ∆≠ 1 (см. кривые 2 , 3 на рисунке 2 в [7]), которая безусловно устойчива в норме пространства С сеточных функций yⁿ_t [1, 7, 19].

На рисунке 2 изображены приближенные решения начальной задачи (1), (52), полученные обобщенными МРК четвертого и шестого порядка точности по τ . Кривые 2 на рисунках 2 а и 2 б определены двухстадийным методом Гаусса–Лежандра и трехстадийными методами Лобатто IIIA и IIIB (согласно (41), все три метода приводят к одному и тому же результату и имеют четвертый порядок точности по τ ); линии 3 рассчитаны трехстадийным методом Лобатто IIIC (в соответствии с (45), этот метод обладает асимптотической спектральной устойчивостью и имеет четвертый порядок по τ ).

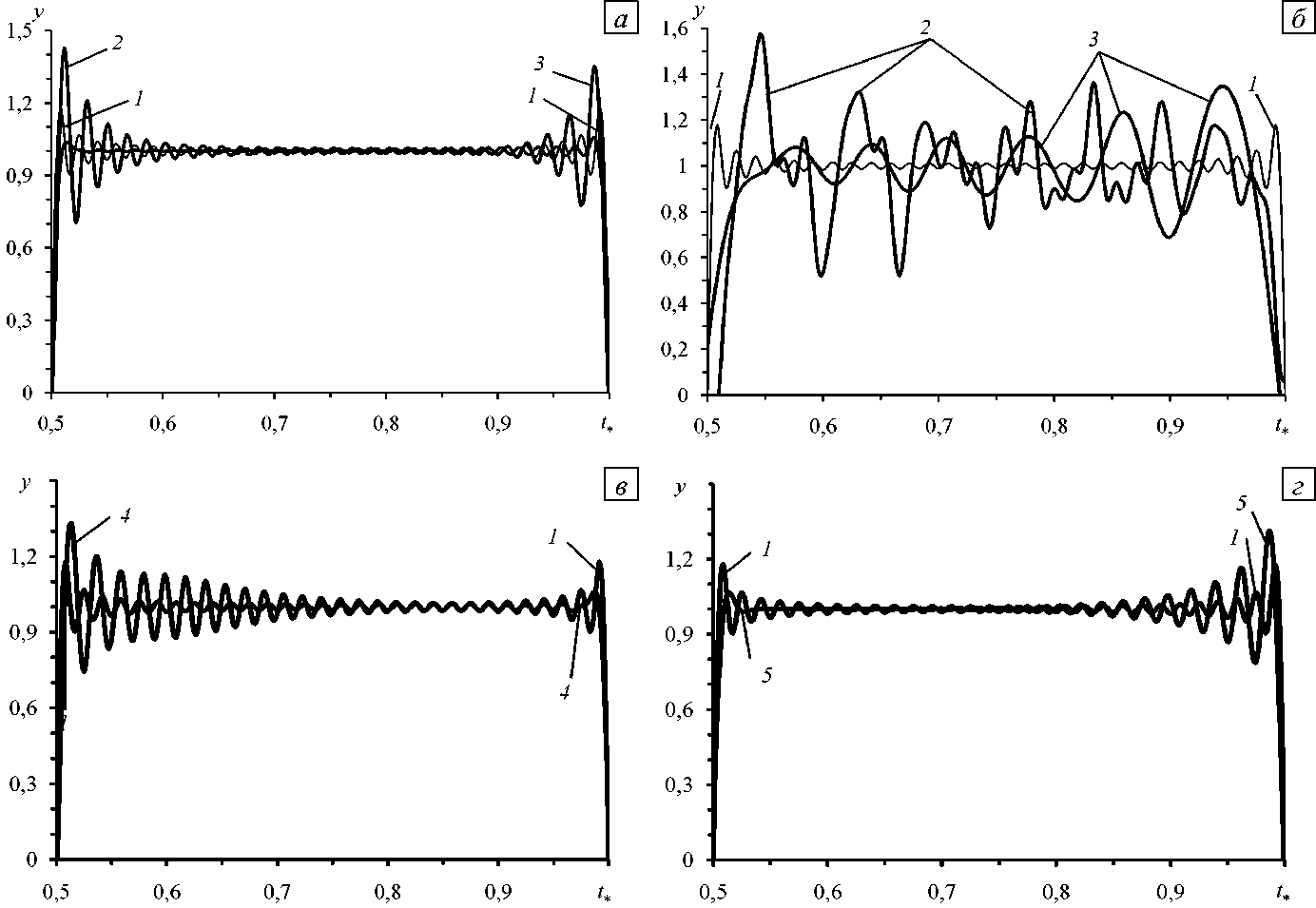
Рис. 2. Характер решений (кривые 2 – 5 ) на основе обобщенных МРК четвертого ( а , б ) и шестого ( в , г ) порядков точности при средних ( N = 50 , см. (62)) ( а ) и больших ( N = 5 ⋅ 10⁴ ) ( б ) временах; 1 – точные решения; 2 – двухстадийный метод Гаусса–Лежандра, трехстадийные методы Лобатто IIIA и IIIB; 3 – трехстадийный метод Лобатто IIIC; 4 – трехстадийный метод Гаусса–Лежандра, четырехстадийные методы Лобатто IIIA и IIIB; 5 – четырехстадийные метод Лобатто IIIC

Вследствие высокого порядка точности указанных методов в окрестности начального момента времени (при малых значениях N в (62)) приближенные решения визуально практически не отличаются от точного решения (от кривой 1 на рисунке 1 а ). С увеличением N в окрестности точек с большими градиентами решения (56) разница между приближенными и точными решениями возрастает и после нескольких десятков колебаний низшей гармоники в решении (55) становится весьма заметной. Это отчетливо наблюдается на рисунке 2 а (при N = 50 ).

Так как кривые 2 на рисунках 2 а и 2 б отвечают обобщенным МРК, для которых выполняется тождество (9), то согласно оценке (60) при больших значениях времени t приближенное решение может существенно отличаться от точного. Последнее нашло свое отражение на рисунке 2 б (при N = 5 ⋅ 10 ⁴ ), где кривая 2 далека от точного решения (от кривой 1 ) и имеет тенденцию к образованию «биений» в приближенном решении. В итоге может сложиться ситуация, аналогичная той, что характеризуется кривой 2 на рисунке 1 б .

Амплитуды гармоник решения (57) (кривые 3 на рисунках 2 а и 2 б ) со временем затухают (так как для метода Лобатто IIIC справедливы неравенства (10)), поэтому аналогичных резких «биений» на кривой 3 рисунка 2 б не наблюдается. Не затухшие к этому времени низшие гармоники обуславливают приближенное решение, которое колеблется в некоторой малой окрестности точного решения.

На рисунке 2 в кривая 4 соответствует приближенному решению задачи (1), (52), полученному при N = 5 - 10 4 (то есть при больших значениях времени t ) на основе трехстадийного метода Гаусса-Лежандра (шестой порядок точности по т ). Дополнительные расчеты по схеме (31)-(40) показали, что приближенные решения на базе четырехстадийных методов Лобатто IIIA и IIIB визуально не отличаются от этой кривой (функции устойчивости для всех названных методов удовлетворяют тождеству (9)). На рисунке 2 г кривая 5 характеризует приближенное решение при N = 5 - 10 4 , определенное четырехстадийным методом Лобатто IIIC, имеющим шестой порядок точности по т и функцию устойчивости, удовлетворяющую неравенствам (10).

Поведение кривых 4 , 5 на рисунках 2 в и 2 г качественно подобно поведению кривых 2 и 3 на рисунке 2 а , поэтому более подробно их обсуждать не будем. Отметим лишь, что при малых и средних значениях времени t решения на основе обобщенных МРК шестого порядка точности визуально не отличаются от точного решения (от кривых 1 на рисунках 1 а и 2 а ).

На рисунке 3 изображены приближенные решения начальной задачи (1), (52), полученные обобщенными МРК третьего порядка точности по т : кривые 2 найдены двухстадийными методами Радо IA и IIA (несмотря на различие формул (42), (43) рассчитанные по ним кривые визуально неразличимы); линии 3 вычислены при помощи двухстадийного диагонального метода (метода Нёрсетта, см. (46)–(48)). В силу достаточно высокого порядка точности указанных методов в окрестности начального момента времени (при малых значениях N в (62)) приближенные решения визуально практически не отличаются от точного решения (от кривой 1 на рисунке 1 а ). Так как эти методы удовлетворяют неравенствам (10), то с увеличением времени t высшие гармоники в разложении (57) затухают, и приближенные решения описывают точное лишь в некотором осредненном смысле, как например на рисунке 3 а (при N = 50). Причем «биения», характерные для приближенных решений, изображенных на рисунке 2 а (хотя порядок точности последних решений выше) не возникают. Согласно (42), (43), (47) с течением времени все гармоники в решении (57) затухают, и при весьма больших значениях t приближенные решения, определенные двухстадийными методами Радо IA, Радо IIA и Нёрсетта, существенно отличаются от точного (см. Рис. 3 б , получено при N = 5 - 10 4 ).

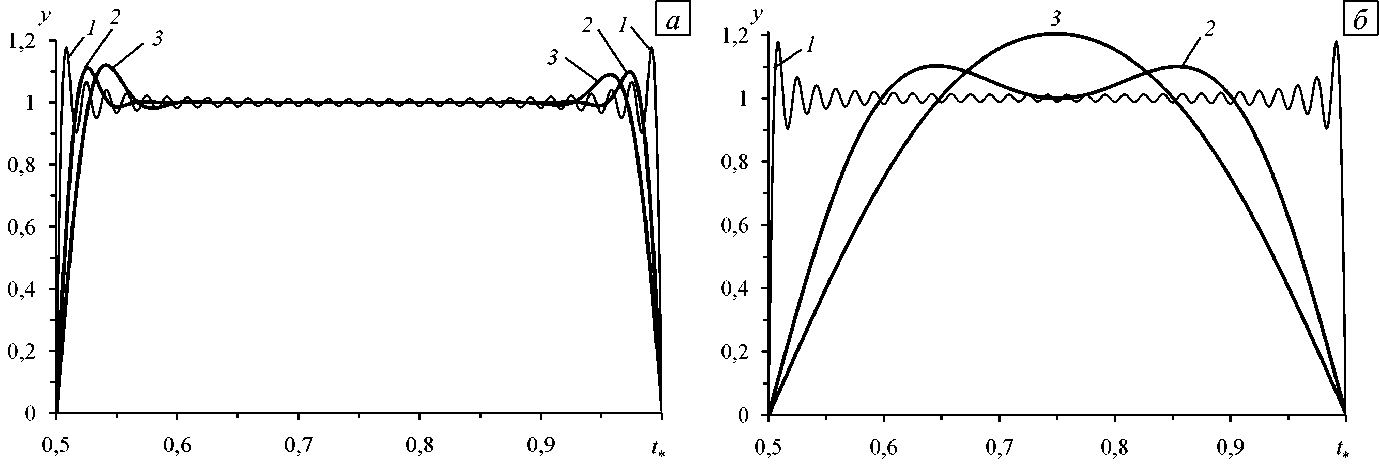
Рис. 3. Характер решений (кривые 2 , 3 ) на основе обобщенных МРК третьего порядка точности при средних ( N = 50, см. (62)) ( а ) и больших ( N = 5 - 10⁴) ( б ) значениях времени; 1 - точные решения; 2 - двухстадийные методы Радо; 3 - метод Нёрсетта

Кривые 2 на рисунке 4 рассчитаны по схеме (31)–(40) трехстадийным методом Радо IA (с пятым порядком точности по т ). Расчет трехстадийным методом Радо IIA приводит к результату, который визуально не отличается от линий 2 . Кривые 3 на рисунке 4 определены методом Барриджа (имеет четвертый порядок точности; см. (50), (51)). Как видно из рисунка 4 а , методы Радо IA и IIA при средних значениях времени t (при N = 50) приводят к приближенным результатам, которые визуально не отличаются от точного решения (кривая 1 ).

Сравнение кривых 3 на рисунках 3 и 4 показывает: из двух рассмотренных выше диагонально неявных обобщенных МРК, по-видимому, с точным решением начальной задачи (1), (52) лучше согласуется метод Нёрсетта (см. кривые 3 на рисунке 3), даже несмотря на то, что его точность на порядок ниже, чем у метода Барриджа (см. кривые 3 на рисунке 4).

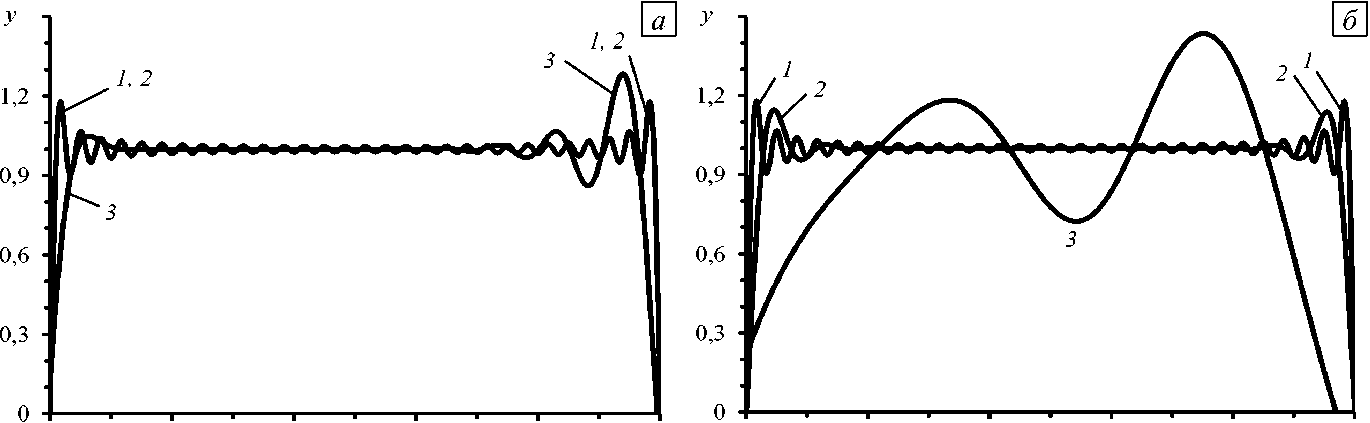
0,5 0,6 0,7 0,8 0,9 t* 0,5 0,6 0,7 0,8 0,9 ^

Рис. 4. Характер решений (кривые 2 , 3 ), найденных обобщенными трехстадийными методами Радо и методом Барриджа при средних ( N = 50 , см. (62)) ( а ) и больших ( N = 5 - 10 4 ) ( б ) значениях времени; 1 - точные решения; 2 - методы Радо (пятый порядок точности); 3 – метод Барриджа (четвертый порядок точности)

• 5.    Заключение

Проведенные исследования показывают, что все явные обобщенные МРК спектрально неустойчивы применительно к численному интегрированию начальной задачи для уравнения переноса. Неявные же обобщенные МРК спектрально устойчивы, причем методы, основанные на формулах Радо, Лобатто IIIC, Нёрсетта и Барриджа, обладают, кроме того, свойством асимптотической устойчивости, которое не присуще обобщенным методам Гаусса–Лежандра, Лобатто IIIA и IIIB. Выполненный сравнительный анализ приближенных численных решений разных порядков точности и аналитического решения начальной задачи для уравнения переноса показывает, что при задании начальных условий с большими по модулю производными первого и высших порядков (качественно подобные условия возникают, например, при рассмотрении волновых процессов в стержневых системах в случаях их продольного ударного нагружения [2, 16]) при средних и больших значениях времени целесообразно использовать двух-и трехстадийные методы Радо IA или Радо IIA, имеющие третий и пятый порядок точности соответственно, или двухстадийный диагонально неявный метод Нёрсетта, обеспечивающий третий порядок точности (следует отметить, что в [16] независимо и на основе совершенно других рассуждений получены аналогичные результаты: при численном решении динамических задач об ударном продольном нагружении стержня целесообразно отдавать предпочтение формулам Радо, а не формулам Лобатто). Преимущество метода Нёрсетта заключается в том, что он является диагональным, а значит, система уравнений (31) с учетом (46) на каждой стадии может быть проинтегрирована последовательно по пространственной переменной x . Использование же методов Радо требует интегрирования систем двух или трех уравнений (31) (в зависимости от числа стадий), которые не распадаются на отдельные уравнения, но зато эти методы обеспечивают наилучшую точность приближенного решения для уравнения переноса при наличии больших градиентов и производных высших порядков.

Работа выполнена при финансовой поддержке РФФИ (проект № 14-01-00102-а).