Исследование структурной значимости функциональных элементов сложных многорежимных объектов

Непрерывное развитие и усложнение космической техники, космических систем и технологий многорежимного управления закономерно предопределяют целесообразность разработки и применения методов исследования надёжности и живучести систем [1], оценивания критичности отказов их функциональных элементов (ФЭ).

Исследование критичности отказов ФЭ системы, иерархизация элементов и подсистем по данному свойству дают возможность определять и совершенствовать в первую очередь узлы и агрегаты с более критичными элементами, а, следовательно, обладающими более высоким приоритетом, наибольшей значимостью при функционировании многорежимных сложных объектов (СлО) с перестраиваемой логической структурой, к которым, несомненно, относятся бортовые системы малых космических аппаратов (МКА).

Необходимо отметить, что критичность отказов элементов СлО представляет собой векторное свойство [2], включающее в себя структурную значимость; возможность локализации отказа; степень тяжести последствий отказа; вероятность отказа элемента; устойчивость элемента к воздействию внешних неблагоприятных факторов; степень резервирования; контролируемость состояния элемента; продолжительность существования риска отказа. Следует отметить, что на различных этапах жизненного цикла СлО при решении задач оценивания, анализа и синтеза облика таких объектов требуется учитывать варианты задействования динамических режимов функционирования, которые существенным образом влияют на структурно-функциональную надёжность и живучесть ФЭ, подсистем и всего объекта в целом.

Проблематика обеспечения высокого качества функционирования таких многорежимных СлО, как автоматический космический аппарат, как правило, связана с необходимостью развития математических средств структурного моделирования и оптимизации [1]. Предлагаемая статья является продолжением работ [3–6], посвящённых исследованию структурно-функциональных свойств и показателей структурной надёжности и живучести многорежимных СлО. В данной статье представлены результаты исследования структурной значимости функциональных элементов (выявления критичности отказов ФЭ с позиции их структурного построения) указанных СлО в зависимости от характера и интенсивности задействования режимов их функционирования.

Следует отметить, что некоторые режимы являются несовместными (т. е. используются поочередно). Отдельные режимы могут быть дополнительными и использоваться одновременно с основными режимами. Кроме того, режимы могут носить регулярный и детерминированный характер, а также вводиться в случае необходимости, которая носит принципиально случайный характер. Поэтому предсказать использование этих режимов на некотором временном интервале можно лишь с некоторой вероятностью. Отличия с точки зрения интенсивности их задействования состоят либо в различных долях времени нахождения в этих режимах на заданном интервале времени, либо в различных значениях вероятности использования на заданном интервале времени. При этом некоторые ФЭ СлО используются только при работе в одном из режимов, в то время как существуют ФЭ, общие для нескольких режимов функционирования СлО.

Интегральные показатели структурной значимости функциональных элементов многорежимных сложных объектов

Для исследования структурной значимости ФЭ многорежимных СлО воспользуемся имеющимися возможностями общего логико-вероятностного метода и программного комплекса логико-вероятностного моделирования «Арбитр» [7]. Построим схему функциональной целостности (СФЦ) СлО (графическое представление логических условий реализации собственных функций ФЭ и режимов функционирования объекта, а также целей моделирования — логических условий реализации исследуемого свойства) и рассчитаем вероятностный полином успешного функционирования СлО [3, 7, 8]. Следует отметить, что при определении вероятностного полинома успешного функционирования СлО учитываются условия совместного и раздельного

(параллельно-последовательного) задействования режимов функционирования СлО.

Пусть вероятностный полином успешного функционирования СлО имеет вид

ℜ(P1, …, Pn, Pn+1, где Pi(Qi = 1 – Pi), i = 1, …, n — вероятности безотказной работы (отказа) ФЭ СлО, а Pn+i(Qn+i = 1 – Pn+i), i = 1, …, m — интенсивности потребности (невос-требования) в реализации режимов функционирования СлО. Обозначим интенсивности задействования режимов функционирования СлО через αi = Pn+i, i = 1, …, m.

Используя параметрический геном структуры [3] многорежимного СлО ^→χ(α₁, …, α _m ) = (χ₀(α₁, …, α _m ), χ₁(α₁, …, α _m ), …, χ _n (α₁, …, α _m )) ^T , представляющий собой вектор коэффициентов полинома (2) успешного функционирования объекта, состоящего из однородных функциональных элементов (т. е. P ₁ = P ₂ = … P_n = P ),

ℜ( P , α₁, α₂, …, α _m ) = χ₀(α₁, α₂, …, α _m ) + χ₁(α₁, α₂, …, α _m ) P + … + χ _n (α₁, α₂, …, α _m ) Pⁿ ,            (2)

можно вычислить значения показателей структурно-функциональной надёжности однородного и неоднородного СлО по следующим формулам:

F    (→χ(α , …, α )) = ℜ(P, α , …, α )dP = →χ(α , …, α ) . 1,   ,   , однор 1 m 0          1 m              1 m        2   3

1 ^T

^, n + 1 ^;

F     (→χ(α , …, α )) = →χ(α , …, α ) . 1,   , 1 , неоднор 1,, m          1,, m , 2 , 22 ,

,

1 2 ⁿ

T

Для определения значимости ФЭ многорежимного СлО вычисляется вероятностный полином (4) как частная производная от коэффициента готовности (вероятности безотказной работы) объекта по коэффициенту готовности (вероятности безотказной работы) элемента [7]

a ^(P , , ..., P , a , , ..., a )

ξ _i ( P ₁, …, P_n , α₁, …, α _m ) =                              = ℜ( P ₁, …, P_n , α₁, …, α _m )| _{P i =1} – ℜ( P ₁, …, P_n , α₁, …, α_m)| _{P i =0}.  (4)

i

Тогда каждому п–олиному ξi(P1, …, Pn, α1, …, αm) (∀i = 1,n) сопоставим соответствующий параметрический геном →χi(α1, α2, …, αm), используя которые можно вычислять структурные значимости ФЭ однородных и неоднородных СлО по вышеприведённым формулам (3). Однако следует отметить, что структурная значимость ФЭ зависит от характера и интенсивности задействования режимов функционирования СлО. Так, помимо раздельного или совместного использования, режимы функционирования могут быть равноценными по интенсивности (α1 = α2 = … = αm = α) или неравноценными. Для указанных четырёх вариантов задействования режимов функционирования сложных объектов, используя подход, предложенный в работах [3–6] для исследования структурной значимости функциональных элементов многорежимных объектов, введём следующие интегральные показатели (5)–(8):

J_pp = m ^{. 1} ∫ ₀ ^{/ m}F _*(^→χ _p (α)) d α;                    (5)

J_cp = ∫ F _*(^→χ _c (α)) d α;                         (6)

функционирования; при совместном задействовании неравноценных по интенсивности режимов функционирования, соответственно.

J = m! × pn                                            (7)

×     ∫∫∫     F*(→χp(α1, …, αm)) dα1dα2 … dαm, а1+ - +а т

0<а <1, i = 1,-, т i

J_cn = ∫∫ ... ∫ F _*(^→χ _с (α₁, …, α _m )) d α₁ d α₂ … d α _m ,   (8)

00    0

Подход к оперативному вычислению значений обобщённых интегральных показателей структурной значимости

где показатели (5) и (6) предназначены для оценивания структурной значимости ФЭ однородных и неоднородных объектов при, соответственно, раздельном или совместном задействовании равноценных по интенсивности режимов функционирования, а показатели (7) и (8) — при, соответственно, раздельном или совместном задействовании неравноценных по интенсивности режимов функционирования. В формулах (5)–(8) в качестве функции F _* могут быть использованы F _однор и F _{неоднор} для соответствующих параметрических геномов ^→χ _p (α), ^→χ _c (α), ^→χ _p (α₁, …, α _m ), ^→χ _c (α₁, …, α _m ).

Здесь

Исходя из вышесказанного, для расчёта значений показателей структурной значимости ФЭ СлО, учитывая при этом характер и интенсивность задействования его режимов функционирования, следует воспользоваться формулами (5)–(8). Обозначим параметрический геном вероятностного полинома значимости некоторого рассматриваемого ФЭ для случая задействования неравноценных (равноценных) по интенсивности режимов функционирования следующим образом: ^→χ(α₁, …, α _m )(^→χ(α)). Тогда для однородного или неоднородного объекта в качестве подынтегральной функции в формулах (5)–(8) используем либо

F _*(^→χ(α₁, …, α _m )) = ^→χ(α₁, …, α _m ) ^.

F _*(χ(α)) = χ(α) ^.

1, ¹ ₂, ¹ ₃,

либо

1, ¹ ₂, ¹ ₃,

…,

1 ^T n + 1 ^;

1 ^T

^…, n + 1 ^,

^→χ _p (α) = ^→χ ⁱ _p (α); ^→χ _c (α) = ^→χ ⁱ _c (α);

^→χ _p (α₁, …, α _m ) = ^→χ ⁱ _p (α₁, …, α _m );

→       →         11

F _*(χ(α₁, …, α _m )) = χ(α₁, …, α _m ) ^. 1, ₂ , ₂ 2 ,

,

2 ⁿ

T

;

^→χ _c (α₁, …, α _m ) = ^→χ ⁱ _c (α₁, …, α _m ) (∀ i = 1, n ) — параметрические геномы значимости ФЭ СлО при раздельном задействовании равноценных по интенсивности режимов функционирования; при совместном задействовании равноценных по интенсивности режимов функционирования; при раздельном задействовании неравноценных по интенсивности режимов

F _*(χ(α)) = χ(α) ^.

…, _{2 n}

T

Следует отметить, что уравнение полинома (1) состоит из мономов, которые включают в себя [6] переменные со степенью либо 0, либо 1. В этом случае подынтегральное выражение в самом общем виде можно представить следующим образом:

F (^→χ(α , …, α )) = β + β α + β α α +        β α α + … + β α α …α .           (9)

*        1,, m          0           i i                ij i j                     ijk i l              12…m 1 2 m i=1              i=1 j=i+1                  i=1 j=i+1 k=j+1                                  …

Используя данное представление подынтегральной функции, осуществим вычисление интегральных показателей структурной значимости функциональных элементов однородного или неоднородного сложного объекта.

Легко увидеть, что формулы (5), (6) и (8) примут следующий вид:

mmm т                                                     ,    e0   1 ₽f 1 1 в»e

J = m •[ F.(X(a))da = m •[ (pn + В Pa +     в а2 + - + P., am)da =----+----+-------+_ +;

^Jpp        0 *^VM ”          0    ⁰ 1^ ^!    1=1 j=i +i ^?            12" m           m ⁰ • 1 m. 2 m² ■ 3         m i™. (m +1)

mmm i             1                                         в 5в,55

Jcp = ∫ F*(χ(α))dα = ∫ (β0 + ∑ βiα + ∑ ∑ βijα2 + … + β12…mαm)dα =   +     ++ о                          о           i-1           i-1 j=i+1                                              123

+ ^в 12...«' .

(m+1) )

Jcn= ∫∫ ... ∫F*(→χ(α1, …, αm))dα1dα2 … dαm = ∫∫ ... ∫(β0 + ∑ βiαi + ∑∑ βijαiαj + … + ооо                               ооо i -1      i -1 j=i+1

m    mm

^{+ β} 12… m α 1 α

в   5 в ,   55 1 в ,

… α )dα dα … dα =   +    + m 1   2 m 2       21

+

₊ ^β 12... m _{2 m}

.

Для формулы (7) в результате её преобразования получим следующее выражение:

Jpn= m! .     ∫∫∫     F*(χ→p(α1, …, αm))dα1dα2 … dαm = а1+ - +a m

0i = 1,-,m i

= m ! ^.      ∫∫∫       (β₀

^а 1 ⁺ - ^{+ a} m <1 0i = 1,-,m i

m     mm

+ βα + βαα + … + β αα

—Y ~ i i      -t =+1 " ij i j           ~ 12™ m 1 2

… α _m ) d α₁ d α₂ … d α _m =

m       mm

∑β ∑ ∑ β в0 + i =1 'i +        i =1 j=i+1 ^y         +    +                   в12... m

1 m + 1   ( m + 1) •( m + 2)       ( m + 1) • ( m + 2) •... • ( m + m )

Поясним полученный результат. Значение интеграла от любого одночлена, состоящего из k ≤ m различных переменных и входящего в многочлен (9),

есть величина постоянная, равная

m! .               α . α i1        i2

^a 1 ⁺ - ^{+ a} m <1

0i = 1,-,m

i

^. α d α d α … d α = i_k     1     2           m

1            1— a i

= m ! ^. ∫ α₁ d α₁ ∫ α₂ d α₂ ...

о             0

1- a i- a 2- ... - a k —1            1- a i— a 2— ... - a k              1- a i— a 2— ... - a m —1

∫       α k^d α k    ∫      ^d α k +1 ^...      ∫       ^d α m^.

(                                  0

Проинтегрировав данный одночлен по переменным α _{k +1}, α _{k +2}, … α _m , получим

следующее выражение:

m !                1            1— a i                1- a i— a 2— ... - a k —1

^. ∫ ^{α d α} ∫ ^α d α ...           (1

– α1 – α2

... – α _k ) ^{m – k .} α _kd α _k.

Последний интеграл данного выражения равен

1– α ₁ – α ₂ – ... – α _{k –1}

∫

α₁ – α₂ – ... – α _k ) ^{m – k .} α _kd α _k

(1 - a 1 - a₂ - ••• - a k _—1) ^{m k +2}

( m - к + 1)( m - к + 2)

Следовательно, m! .

∫∫∫ a1+ - +a m <1

0i = 1,-,m

i

^α i ₁ ^{. α} i ₂

^. α d α d α … d α = i_k    1     2 m

^. ∫ (1 – α ) ^{m + k – 2 .} α d α =                                 .

m !. ( m + 1). ( m + 2) ^. ... ^. ( m + k - 2) о                            ( m + 1) • ( m + 2) • ... • ( m + k )

Иллюстративный пример

Проведём исследование структурной значимости функциональных элементов системы управления движением и навигации (СУДН) малого космического аппарата дистанционного зондирования Земли (МКА ДЗЗ) с учётом следующих режимов управления угловым движением [9, 10]:

• •    сброса кинетического момента (СКМ);

• •    одноосной солнечной ориентации (ОСО);

• •    трёхосной ориентации в орбитальной системе координат (ОСК);

• •    целевого режима ориентации МКА (ЦО), предназначенного для съёмки заданной области (объекта наблюдения).

В данной работе воспользуемся результатами, представленными в статье [4]. Приведём некоторые из них. В качестве датчиков первичной информации СУДН МКА привлекаются: одноосные измерители угловой скорости (ОИУС), 4 шт.; оптические солнечные датчики (ОСД), 2 шт.; звёздные датчики (ЗД), 2 шт.; приборы ориентации по Земле (ПОЗ), 2 шт. Рассматривается одна из схем ориентации осей четырёх ОИУС — кубическая конфигурация, когда три ОИУС расположены соосно осям МКА и четвёртый — по диагонали куба. Схема функциональной целостности ФЭ СУДН МКА рассматриваемой конфигурации при выполнении указанных выше режимов функционирования СУДН представлена на рис. 1.

Основные функциональные вершины СФЦ отражают: 1 , 2 , 3 и 4 — работоспособность ОИУС1, ОИУС2, ОИУС3 и ОИУС4, соответственно; 5 — работоспособность ОСД1; 6 — работоспособность ОСД2; 7 — работоспособность ПОЗ1; 8 — работоспособность ПОЗ2; 9 — работоспособность ЗД1; 10 — работоспособность ЗД2; 11 — потребность в режиме СКМ; 12 — потребность в режиме ОСО; 13 — потребность в режиме ОСК; 14 — потребность в режиме ЦО. Вершины 15–33 являются фиктивными и описывают реальные логические взаимосвязи элементов СУДН МКА [7].

Используя программный комплекс логико-вероятностного моделирования «Арбитр» [3], получим для СФЦ СУДН

МКА два вероятностных полинома успешного его функционирования:

ℜ c ( P 1 , …, P 10 , P 11 , …, P 14 , Q 1 , …, Q 10 , Q 11 , …, Q 14 );

ℜp(P1, …, P10, P11, …, P14, Q1, …, Q10, Q11, …, Q14), где ℜc(P1,…, P10, P11, …, P14, Q1, …, Q10, Q11,…, Q14) — вероятностная функция проведения успешной ориентации МКА СУДН для режимов, не являющихся группой несовместных событий (ГНС); ℜp(P1, …, P10, P11, …, P14, Q1, …, Q10, Q11, …, Q14) — вероятностная функция проведения успешной ориентации МКА СУДН для реж–имов, представляющих ГНС; Pi(Qi), i = 1,10 — вероятности безотказной раб–оты (отказа) ФЭ СУДН, а P10+i(Q10+i), i =1,4 — интенсивности (вероятности) реализации режимов функционирования СУДН.

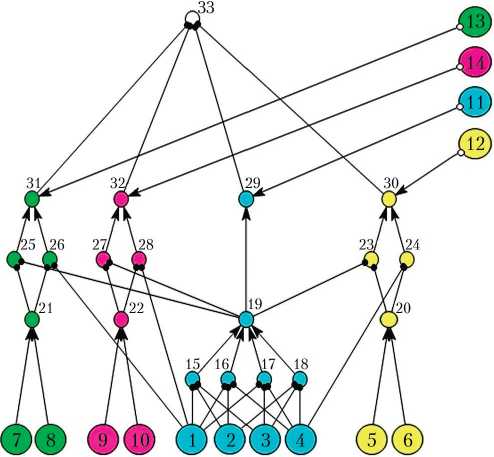
Рис. 1. Структурно-функциональная схема функциональных элементов системы управления движением и навигации для конфигурации «Куб»

Определив для каждого i -го ФЭ полином значимости по формуле (4) для случаев наличия и отсутствия ГНС среди режимов функционирования и соответствующие им параметрические геномы ^→χ ⁱ _с (α₁, α₂, α₃, α₄), ^→χ ⁱ _р (α₁, α₂, α₃, α₄), вычислим полиномы (9) для однородной F _однор(^→χ ⁱ _с (α₁, …, α₄)), F _однор(^→χ ⁱ _р (α₁, …, α₄)) и неоднородной F _{неоднор}(^→χ ⁱ _с (α₁, …, α₄)), F _{неоднор}(^→χ ⁱ _р (α₁, …, α₄)) структур СУДН МКА.

Так, например, для ОИУС1 эти полиномы имеют следующий вид:

F _однор(^→χ ¹ _с (α₁,…, α₄)) = 0,25α₁ + 0,066667α₂ + 0,433333α₃ + 0,433333α₄ – 0,11667α₁α₂ –

– 0,48333α1α3 – 0,48333α1α4 – 0,46429α2α3– 0,13095α2α4 – 0,55357α3α4 +

+ 0,482143α1α2α3 + 0,14881α1α2α4 + 0,577381α1α3α4 + 0,386508α2α3α4 – 0,40079α1α2α3α4;

F    (→χ1(α ,…, α )) = 0,375α + 0,09375α + 0,65625α + 0,65625α – 0,1875α α – неоднор с 1,,   4          ,         1       ,             2       ,             3      ,             4       ,           1 2

– 0,75α1α3 – 0,75α1α4 – 0,5α2α3– 0,4375α2α4 – 0,82031α3α4 + 0,523438α1α2α3 +

+ 0,460938α1α2α4 + 0,851563α1α3α4 + 0,5625α2α3α4 – 0,57617α1α2α3α4;

F _однор(^→χ ¹ _р (α₁,…, α₄)) = 0,25α₁ + 0,066667α₂ + 0,433333α₃ + 0,433333α₄;

F    (^→χ ¹ (α ,…, α )) = 0,375α + 0,09375α + 0,65625α + 0,65625α .

неоднор p 1       4                  1                   2                   3                   4

Результаты вычислений структурной значимости ФЭ при совместном или раздельном задействовании (без ГНС и с ГНС, соответственно) равноценных или неравноценных режимов функционирования однородной или неоднородной СУДН МКА приведены в таблице и на рис. 2.

По оси абсцисс откладываются номера ФЭ рассматриваемой СУДН МКА, а по оси ординат — значения структурной значимости для каждого элемента. Для наглядности точки соединены линиями.

Проведя анализ полученных результатов, можно сделать следующие выводы.

Во-первых, для любого варианта задействования режимов функционирования наиболее значимыми являются ФЭ1, ФЭ2, ФЭ3, ФЭ4 — это ОИУС. Причём наиболее структурно значимым является ОИУС1, за ним следует ОИУС4, затем — ОИУС2 и ОИУС3. Максимальную значимость эти ФЭ приобретают в случае раздельного задействования неравноценных по интенсивности режимов функционирования, когда СУДН МКА состоит из неоднородных по вероятности безотказной работы ФЭ. Остальные элементы имеют почти одинаковую значимость, существенно отличающуюся от значимостей упомянутых выше ОИУС.

Значения структурной значимости ФЭ СУДН МКА

Номера критичных ФЭ	Режимы с ГНС				Режимы без ГНС
	Равноценные		Неравноценные		Равноценные		Неравноценные
	Неоднор.	Однор.	Неоднор.	Однор.	Неоднор.	Однор.	Неоднор.	Однор.
ФЭ1	0,22266	0,14792	0,35625	0,23667	0,22656	0,16617	0,29309	0,20794
ФЭ2	0,08203	0,05625	0,13125	0,09000	0,14160	0,11119	0,17224	0,13008
ФЭ3	0,08203	0,05625	0,13125	0,09000	0,14082	0,11000	0,17126	0,12860
ФЭ4	0,15234	0,10208	0,24375	0,16333	0,18438	0,13927	0,23157	0,16895
ФЭ5	0,03516	0,02292	0,05625	0,03667	0,06322	0,04474	0,07166	0,04878
ФЭ6	0,03516	0,02292	0,05625	0,03667	0,06322	0,04474	0,07166	0,04878
ФЭ7	0,03516	0,02292	0,05625	0,03667	0,06517	0,04508	0,07556	0,04998
ФЭ8	0,03516	0,02292	0,05625	0,03667	0,06595	0,04627	0,07654	0,05146
ФЭ9	0,03516	0,02292	0,05625	0,03667	0,06517	0,04508	0,07556	0,04998
ФЭ10	0,03516	0,02292	0,05625	0,03667	0,06595	0,04627	0,07654	0,05146

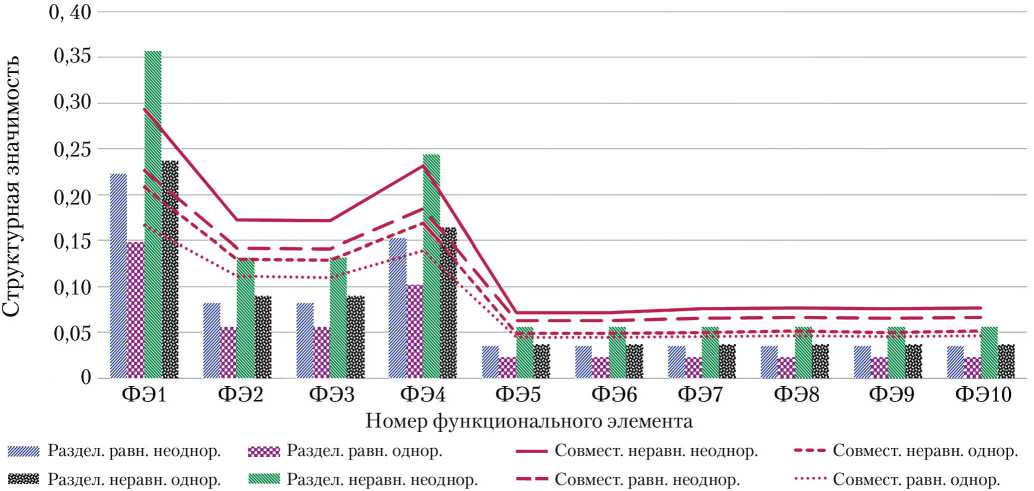
Рис. 2. Структурная значимость функциональных элементов системы управления движением и навигации малого космического аппарата для конфигурации «Куб»

Во-вторых, если значение структурной значимости ОИУС1 принять за 100%, то при раздельном задействовании режимов структурная значимость остальных ФЭ будет иметь следующие доли от этого значения (независимо от равноценности режимов и однородности объекта): для ОИУС4 она составляет 68–69%; для ОИУС2 и ОИУС3 — 37–38%; для ОСД, ПОЗ и ЗД эта доля составит ~15%. При совместном задействовании режимов (независимо от равноценности режимов и однородности объекта) эти доли составят: для ОИУС4 79–84%; для ОИУС2 и ОИУС3 — 59–67%; для ОСД, ПОЗ и ЗД — 23–29%. Другими словами, при совместном использовании режимов функционирования СУДН МКА при проведении ориентации структурная значимость ОИУС становится более однородной, а для всех остальных ФЭ она возрастает в два раза в отличие от варианта раздельного задействования режимов.

Заключение

Для исследования структурной значимости ФЭ многорежимных объектов с перестраиваемой структурой был построен полином значимости каждого элемента, определяемый как результат дифференцирования вероятностного полинома успешного функционирования СлО по переменной, характеризующей вероятность безотказной работы конкретного ФЭ СлО. С использованием концепции параметрического генома и ранее введённых формул вычисления структурно-функциональной надёжности многорежимных СлО с перестраиваемой структурой разработаны показатели структурной значимости ФЭ, отражающие вклады в структурнофункциональную надёжность объекта при переводе ФЭ из неработоспособного состояния в работоспособное с учётом характера и интенсивности режимов его функционирования. Приведены и доказаны формулы оперативного вычисления значений обобщённых интегральных показателей структурно-функциональной надёжности многорежимных СлО, применение которых позволит повысить производительность решения задач анализа и синтеза конфигурации облика объекта при реализации указанных операций на борту МКА. Рассмотрен пример исследования структурной значимости ФЭ СУДН МКА для четырёх режимов ориентации МКА. Анализ приведённых результатов показал, что особенности задействования режимов функционирования СлО влияют на значения структурной значимости его ФЭ. Кроме того, при решении задач оценивания структурно-функциональной живучести многорежимного СлО, а также задач структурно-функционального синтеза облика рассматриваемых объектов на этапах создания и проектирования, следует учитывать различные варианты совместного или раздельного задействования режимов, характер их интенсивности и однородность объекта.

Исследования, выполненные по данной тематике, проводились при частичной финансовой поддержке грантов РФФИ (№ 20-08-01046) в рамках бюджетной темы FFZF–2022–0004.