Исследование температурной зависимости энергии активации стеклования некоторых неорганических веществ
Автор: Машанов А.А., Дармаев М.В., Лупсанов С.Б.
Журнал: Вестник Бурятского государственного университета. Химия. Физика @vestnik-bsu-chemistry-physics
Статья в выпуске: 2, 2024 года.
Бесплатный доступ
Предложен метод определения энергии активации процесса стеклования в зависимости от температуры с использованием ряда Тейлора на примере: SiO2-Na2O-CaO, SiO2-PbO и оптических стекол. Результаты расчетов показали, что зависимость U(T) для указанных систем вполне удовлетворительно описывается полиномом второй степени. Цель настоящей работы - сравнить значения коэффициентов, полученных из разложения U(T) в ряд Тейлора, с характеристиками кривых U(T) от (T -Tg), полученных непосредственно из экспериментальных температурных значений вязкости. В качестве объектов исследования мы выбрали указанные ранее составы стекол, поскольку для этих материалов имеются экспериментальные данные по вязкости в широком диапазоне температур. Для них приемлемо разложение функции энергии активации U(T) в ряд Тейлора. Предложенный метод может быть расширен за счет включения других стеклообразующих составов.
Стеклование, вязкость, энергия активации, ряд тейлора, уравнение вильямса-ландела-ферри, стекло
Короткий адрес: https://sciup.org/148328733
IDR: 148328733 | УДК: 539.213 | DOI: 10.18101/2306-2363-2024-2-49-56
Текст научной статьи Исследование температурной зависимости энергии активации стеклования некоторых неорганических веществ
Процесс превращения аморфного вещества из жидкого в стеклообразное состояние остается одной из неразгаданных загадок. Стеклование жидкости напрямую зависит от увеличения вязкости при охлаждении расплава, при этом энергия активации стеклования обычно совпадает с энергией активации вязкого течения в переходной области жидкость-стекло.
Для описания температурной зависимость вязкости простых жидкостей чаще всего используется уравнение Я. И. Френкеля [1]
I U 1
n = n0 exp| RTI ’ где η0 — предэкспоненциальный множитель, R — газовая постоянная, U — энергия активации вязкого течения, которая достаточно сильно зависит от температуры. В связи с этим есть альтернативное уравнение ВЛФ (Вильямса-Ландела-Ферри), в котором исключена зависимость U(T) [2; 3]
In a T = —C 1
T - T g
T - T g + C 2 ’
_ At) _ v(t) aT=T^=П^ •
Эмпирические постоянные С 1 и С 2 не зависят от температуры, Tg — обозначает температуру стеклования, а τ — время релаксации. Известно, что уравнение ВЛФ правильно описывает молекулярно-кинетические процессы в области стеклования и достаточно точно обеспечивает температурную зависимость времени релаксации τ ( T ) и вязкости η ( T ) в интервале температур стеклования для различных аморфных материалов. В работах [2; 4] было показано, что уравнения (1) и (2) справедливы для различных стеклообразующих систем.
В работе [5; 6] предложен вывод уравнения ВЛФ без конкретизации функций τ ( Т ) и η ( Т )
In aT =
I41 к B I
T - Tg
T - T g + ,T к B
,
A = -
d ln n dTITj
,
TT
B = 1 52 ln n ~ 2 д ( т / Tg )2
T = T
,
Функция ln η ( Т ) была разложена в ряд вблизи Tg с использованием малого безразмерного параметра 1 = (T — T g )/Tg [5; 6]-
Постоянные уравнения ВЛФ (2) получают физическую интерпретацию в виде выражения через производные А и B .
c = —
-
1 B ,
C = AT
-
2 B g .
Разложение в ряд Тейлора функции U ( T )
Разложим в ряд Тейлора функцию U ( T ) вблизи температуры стеклования по малому приращению температуры ( T — T g ), ограничимся только первыми тремя членами ряда [7]
U = ^ - D 1 ( T - T g ) + D 2 ( T - T g )2 ,
D, =-[ —
1 {dT
D 2
1 (д 2U
V
2^ dT 2 J
Tg
Параметром малости в разложении (8) является безразмерная величина 1 = ( T — T g )/T g , но T g в первой и второй степени скрыто в коэффициентах D 1 и D 2 .
Представим уравнение (1) в виде ln n = ln n 0
1 U
+ , RT
при U = u(t )
и возьмем производную
д ln n _
d(T/Tg)=
T g
1 (dU
R T {dT
U
T 2
.
Согласно равенству (4), получаем соотношение d In n =-d(T/Tg)
T = T g
1 R
dU l dT )T
Tg
U g T g
= Dr + , R RT g
В этом соотношении D 1 определена производной (9).
Из выражений (6) и (7) получаем
A = — T .
C 2 g
Приравнивая правые части равенств (12) и (13), приходим к соотношению
D = CRT- 1
C 2
U g T g ,
которое с учетом Ug = C 1 RTg преобразуется в уравнение:
( T ^
D = CR^-1 ,
{C 2 7
Формулу для коэффициента D 2 находим следующим образом:
1 d2 ln n Tg д ( d ln n
2 d ( T/Tg ) " 2 dT { dT
T g 2
1 dU U
2R dT T dT T 2
T 2 = — ^
1 ( d 2U ^
2R [T{dT
H
1 ( ди
T 2 {dT
H
1 (dU ) 2U I I +
T 2 {dT 7 T 3
,
B _ 1 д2 ln^ = 2 d(T/Tg)
T _T g
Tg R
I n D U g
DD ++
I 2 T g T g
>
.
Здесь D 1 и D 2 определены производными (9) и (10). Подставим в последнее соотношение уравнение (14), получим
в _ Tg-dd, +1 [ C RT, V C2
T
R
T g
U g 1 т
g 7
T
Ug Tg L
+ —g J_ S D +
T g
R
CR
■CT J
>
.
Из выражений (7) и (13) имеем в _ T I-
2 g
C 2
Подставляем последнюю формулу в равенство (17), получаем окончательно для D 2 уравнение:
T
D 2 _ C R —
C 2
с
V '-'2
1 -
Таким образом, с помощью формул (8), (15) и (18) можно рассчитать зависи- мость энергии активации процесса стеклования от температуры.
В таблице 1 приводятся коэффициенты D 1 и D 2 для исследуемых стекол, которые сопоставлены с характеристиками кривых U от ( T — T g ), полученных непосредственно из экспериментальных данных о температурной зависимости вязкости. Примеры расчета коэффициентов кривой U от ( T — Tg ) как полинома второй и третьей степени с помощью программы Microsoft Excel показаны на рис. 1– 3.
Таблица 1 Сопоставление параметров уравнений (15) и (18) с полиномами 2-й и 3-й степени
|
№ |
Стекло, мол. % |
Расчет по (15) и (18) |
Полином 2-й степени |
Полином 3-й степени |
|||||
|
D 1 |
D 2 |
D 1 |
D 2 |
D 1 |
D 2 |
||||
|
SiO 2 |
Na 2 O |
CaO |
|||||||
|
1. |
75 |
20 |
5 |
0.206 |
0.0007 |
0.229 |
0.0002 |
0.344 |
0.0005 |
|
2. |
75 |
15 |
10 |
0.224 |
0.0008 |
0.274 |
0.0002 |
0.393 |
0.0006 |
|
3. |
70 |
25 |
5 |
0.235 |
0.0009 |
0.274 |
0.0002 |
0.405 |
0.0007 |
|
4. |
70 |
20 |
10 |
0.251 |
0.0010 |
0.300 |
0.0002 |
0.424 |
0.0007 |
|
5. |
70 |
15 |
15 |
0.292 |
0.0012 |
0.343 |
0.0003 |
0.506 |
0.0009 |
|
6. |
65 |
30 |
5 |
0.242 |
0.0010 |
0.287 |
0.0002 |
0.416 |
0.0007 |
|
7. |
65 |
25 |
10 |
0.247 |
0.0010 |
0.305 |
0.0002 |
0.422 |
0.0007 |
|
8. |
75 |
25 |
- |
0.201 |
0.0007 |
0.219 |
0.0002 |
0.346 |
0.0006 |
|
9. |
70 |
30 |
- |
0.235 |
0.0010 |
0.245 |
0.0002 |
0.391 |
0.0007 |
|
SiO 2 |
PbO |
||||||||
|
1. |
59.73 |
40.27 |
0.367 |
0.0021 |
0.326 |
0.0002 |
0.533 |
0.0009 |
|
|
2. |
57.93 |
42.07 |
0.320 |
0.0016 |
0.343 |
0.0003 |
0.489 |
0.0007 |
|
|
3. |
55.36 |
44.64 |
0.346 |
0.0018 |
0.406 |
0.0003 |
0.553 |
0.0009 |
|
|
4. |
52.75 |
47.25 |
0.368 |
0.0021 |
0.433 |
0.0004 |
0.597 |
0.0011 |
|
|
5. |
51.27 |
48.73 |
0.414 |
0.0026 |
0.480 |
0.0005 |
0.644 |
0.0012 |
|
|
6. |
50.46 |
49.54 |
0.390 |
0.0023 |
0.469 |
0.0005 |
0.621 |
0.0012 |
|
7. |
49.76 |
50.24 |
0.394 |
0.0024 |
0.491 |
0.0005 |
0.624 |
0.0011 |
|
8. |
48.81 |
51.19 |
0.427 |
0.0028 |
0.517 |
0.0005 |
0.656 |
0.0012 |
|
9. |
47.75 |
52.25 |
0.418 |
0.0027 |
0.522 |
0.0006 |
0.673 |
0.0013 |
|
10. |
44.98 |
55.02 |
0.426 |
0.0027 |
0.569 |
0.0007 |
0.735 |
0.0017 |
|
11. |
42.47 |
57.53 |
0.454 |
0.0031 |
0.596 |
0.0008 |
0.789 |
0.0020 |
|
12. |
39.84 |
60.16 |
0.512 |
0.0039 |
0.693 |
0.0010 |
0.874 |
0.0023 |
|
13. |
37.71 |
62.29 |
0.513 |
0.0038 |
0.773 |
0.0012 |
0.853 |
0.0019 |
|
Оптические стекла |
||||||||
|
1. |
К8 |
0,147 |
0,0004 |
0,242 |
0,0001 |
0,491 |
0,0006 |
|
|
2. |
К14 |
0,170 |
0,0005 |
0,198 |
0,0001 |
0,411 |
0,0004 |
|
|
3. |
БК4 |
0,106 |
0,0002 |
0,193 |
0,0001 |
0,342 |
0,0003 |
|
|
4. |
БК10 |
0,203 |
0,0006 |
0,278 |
0,0001 |
0,575 |
0,0007 |
|
|
5. |
ТК20 |
0,233 |
0,0007 |
0,525 |
0,0003 |
0,854 |
0,0011 |
|
|
6. |
ТК23 |
0,319 |
0,0012 |
0,607 |
0,0005 |
1,277 |
0,0026 |
|
|
7. |
БФ11 |
0,230 |
0,0007 |
0,436 |
0,0003 |
0,780 |
0,0010 |
|
|
8. |
БФ12 |
0,129 |
0,0003 |
0,258 |
0,0001 |
0,508 |
0,0007 |
|
|
9. |
ЛФ5 |
0,067 |
0,0001 |
0,124 |
0,0001 |
0,246 |
0,0002 |
|
|
10. |
ЛФ9 |
0,174 |
0,0006 |
0,277 |
0,0001 |
0,554 |
0,0007 |
|
|
11. |
ТФ1 |
0,128 |
0,0004 |
0,167 |
0,0001 |
0,310 |
0,0003 |
|
|
12. |
ТФ10 |
0,205 |
0,0008 |
0,280 |
0,0002 |
0,450 |
0,0006 |
|
|
13. |
ОФ1 |
0,103 |
0,0003 |
0,163 |
0,0001 |
0,311 |
0,0003 |
|
В широком диапазоне температур значительное влияние оказывает кубический член в разложении U(T) в ряд Тейлора. Для этого мы аппроксимируем экспериментальные данные кривой U от (T — Tg) как квадратичный полином. Мы приходим к заключению, что зависимость температуры U(T) в широком диапазоне для изученных стекол достаточно точно описывается квадратичным полиномом.
U ( T ), кДж/моль
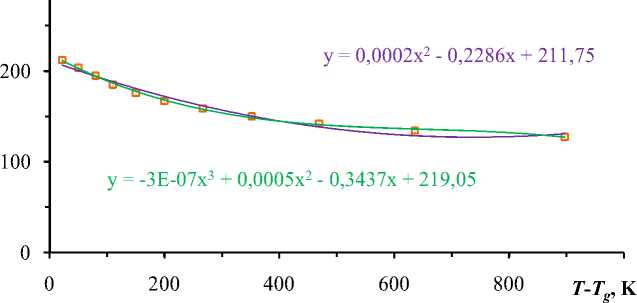
Рис. 1. Результаты обработки температурной зависимости энергии активации вязкого течения стекла SiO 2 -Na 2 O-CaO. Содержание SiO 2 — 75 мол.%, Na 2 O — 20 мол.%, CaO — 5 мол.%. Квадратики — экспериментальные данные1, кривые — полиномы
-
1 MDL® SciGlass — 7.8. Institute of Theoretical Chemistry, Shrewsbury, MA, 2012.
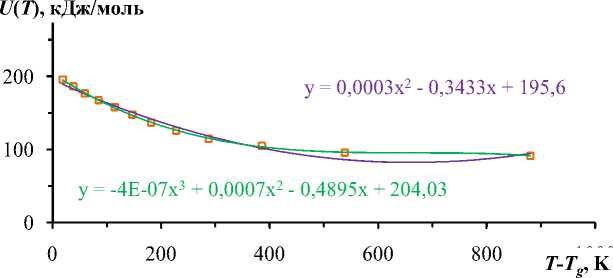
Рис. 2. Результаты обработки температурной зависимости энергии активации вязкого течения стекла SiO 2 -PbO. Содержание SiO 2 — 57,93 мол.%, PbO — 42,07 мол.%. Квадратики — экспериментальные данные1, кривые — полиномы.
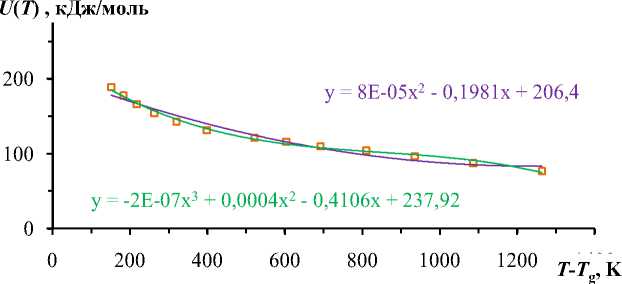
Рис. 3. Результаты обработки температурной зависимости энергии активации вязкого течения оптического стекла К14. Квадратики — экспериментальные данные2, кривые — полиномы.
Заключение
Продемонстрировано разложение зависимости U(T) в ряд Тейлора около Tg. Исследования показали, что температурная зависимость энергии активации для систем SiO2-Na2O-CaO, SiO2-PbO и оптических стекол хорошо аппроксимируется квадратичным полиномом.
Список литературы Исследование температурной зависимости энергии активации стеклования некоторых неорганических веществ
- Френкель Я. И. Кинетическая теория жидкостей. Москва; Ленинград: Изд-во АН СССР, 1945. 425 с. Текст: непосредственный.
- Ферри Дж. Вязкоупругие свойства полимеров. Москва: Изд-во иностр. лит-ры, 1963. 536 с. Текст: непосредственный.
- Williams M. L., Landel R. F., Ferry. J. D. J. Amer. Chem. Soc. 1955; 77, 14: 3701.
- Сандитов Д. С., Бартенов Г. М. Физические свойства неупорядоченных структур. Новосибирск: Наука, 1982. 259 с. Текст: непосредственный.
- Сандитов Д. С., Разумовская И. В. Новый подход к обоснованию уравнения Вильямса-Ландела-Ферри // Высокомолек. соед. Сер. А. 2018. Т. 60, № 2. С. 110-115. Текст: непосредственный. EDN: YSJEST
- Разумовская И. В., Бартенов Г. М. Стеклование жидкости как процесс вымерзания акустических частот // Стеклообразное состояние: труды V Всесоюз. совещ. по стеклообразному состоянию. Ленинград: Наука, 1971. С. 34-38. Текст: непосредственный.
- Сандитов Д. С., Разумовская И. В., Машанов А. А. О температурной зависимости энергии активации стеклования // Высокомолек. соед. Сер. А. 2020. Т. 62, № 5. С. 392400. Текст: непосредственный. EDN: JIJIYK


