Исследование теплопроводности композитных материалов с шаровидным наполнителем

Для многих отраслей промышленности представляет интерес исследование материалов, которые содержат различного рода дисперсные включения. Интерес продиктован рядом проблем, имеющихся как при определении теплопроводности, так и в методах расчёта. Оптимальным был бы учёт всех факторов: размера дисперсионных включений, их формы, пористости композита, термического сопротивления на границе двух фаз и другого [1–5].

Эффективные характеристики композитных материалов обычно  устанавливаются или путём теплофизических измерений, или по аналитическим зависимостям. Впервые аналитические формулы

для вычисления эффективных коэффициентов теплопроводности при различных концентрациях включений и отношениях теплопроводностей были представлены Максвеллом [1], Мередитом [2-4], Релеем [3] и Бруггеманом [3, 4]. Большое количество моделей рассмотрено в работах [5-9].

Другой подход к решению задачи определения эффективных коэффициентов позволяет реализовать численная гомогенизация. Методы численной гомогенизации условно можно разделить на три класса: 1) методы, использующие теорию осреднения дифференциальных операторов; их основным недостатком является невозможность учёта сложной структуры наполнителя, и поэтому они могут применяться только при равномерном распределении включений; 2) методы на основе конечно-элементных или конечноразностных дискретизаций исходных дифференциальных операторов ; но их использование на практике затруднено из-за катастрофически возрастающей размерности дискретных аналогов реальной задачи и к тому же может приводить к потере точности решения системы линейных алгебраических уравнений и увеличению времени расчётов; 3) многомасштабные конечно-элементные методы — класс методов, отличающихся от классического специальной процедурой построения базисных функций; он позволяет разработать вычислительную схему с высокой степенью параллелизации, что обеспечивает значительное сокращение времени решения дискретной задачи без потери точности вычисления эффективного коэффициента; полученные с их помощью результаты сравниваются затем с опытными данными для различного расположения включений и делается вывод об адекватности/неадекватности модели и устанавливаются границы применимости построенных аналитических формул [6].

В [5] отмечается, что «…в публикациях, посвящённых исследованию гетерогенных структур, частицы наполнителя образуют агрегаты и агломераты, а при наличии нескольких соединений наполнителя — конгломераты. …На практике согласие известных аналитических формул эффективной теплопроводности и экспериментальных данных, за исключением модельных экспериментов, достигается путём конструирования формул с использованием метода инверсии компонентов и определения эффективной теплопроводности агломератов наполнителя [3]». Такой метод может быть применен и для включений, форма которых отлична от сферической [6, 7].

Задача теплопроводности в гетерогенных материалах математически аналогична задачам электропроводности, диэлектрической проницаемости и магнитной проницаемости [10, 11]. Их изучение восходит к ранним работам Максвелла [1]. Позднее предложено множество моделей, позволяющих прогнозировать эффективную теплопроводность у различных типов композиционных материалов при достаточно высоких значениях коэффициента теплопроводности наполнителя [12]. В большинстве ранних моделей межфазное тепловое сопротивление в композитах не учитывалось. Однако в последующем выяснилось, что термическое сопротивление может оказывать большое влияние на свойства композитов [6, 9, 12-15]. Первые выражения для теплопроводности композиционных материалов были получены путём модификации оригинальной модели Максвелла [13-16].

При прохождении тепла через границу раздела между компонентами композита происходит падение температуры. Это возмущение теплового потока можно назвать термическим сопротивлением и представить как сумму межфазного и граничного термических сопротивлений, последнее из которых возникает из-за различий физических свойств составляющих композит материалов. В случае неучёта термического сопротивления соотношения для расчёта коэффициента теплопроводности композитов дают их приближённые значения [17].

Межфазное тепловое сопротивление возникает по многим причинам, таким как относительная шероховатость поверхности включений, неоднородность распределения наполнителя и плохое химическое или механическое сцепление компонентов [12], что приводит к скачку температуры на границе раздела «включение-основной материал». Такое межфазное тепловое сопротивление снижает теплопроводность композитов. Важным фактором является и то, что теплопроводность матрицы (основного материала) анизотропна, то есть она зависит от направления приложенного теплового потока.

Экспериментальные исследования дисперсных композитов показывают, что добавление проводящих частиц повышает их эффективную теплопроводность [18, 19]. С уменьшением среднего радиуса частиц эффективная теплопроводность уменьшается, а площадь межфазного контакта на единицу объёма вкючения увеличивается. По-видимому, в таких случаях термическое сопротивление начинает играть значительную роль в общем процессе теплопередачи [20].

Стоит отметить, что Максвелл первым вывел аналитические выражения для эффективной проводимости гетерогенной среды и опубликовал в своей знаменитой работе по электричеству и магнетизму [1]. Он рассмотрел проблему тепловой проводимости включений, вложенных в непрерывную матрицу. Модель Максвелла предполагает отсутствие теплового взаимодействия между дисперсными включениями, то есть тепловым взаимодействием между частицами наполнителя она пренебрегает.

Поскольку теплопроводность композита зависит от теплопроводности составляющих его материалов и их взаимного расположения, то можно оптимизировать это свойство путём структурного проектирования. Компьютерное моделирование стало важным подходом в разработке материалов с различного рода наполнителями, позволяющим уменьшить стоимость и сроки их внедрения в производство. Поэтому создаются программные комплексы проектирования материалов с дисперсными включениями, обладающих требуемой теплопроводностью, базирующиеся на подборе компонентов, и эти «…комплексы могут быть эффективным инструментом поддержки принятия решений при проектировании конструкций и прогнозировании их свойств» [20, 21].

Значительный прогресс за последние годы и в аналитическом описании таких материалов [4–11, 22]. Стало возможным учитывать разную форму включений и их ориентацию. Однако любая из представленных в названных работах формул использует относительно грубую модель гетерогенной среды, что сказывается на точности вычисления коэффициентов теплопроводности. Экспериментальные методы их определения также имеют ограничения (размер исследуемого образца, контрастность свойств системы «матрица–включение» и другое) [3–6, 9, 18, 19, 22, 23].

Итак, для проектирования и создания композитов с требуемыми характеристиками необходимо понимать и уметь прогнозировать их теплопроводность. Предшествующие многочисленные исследования были сосредоточены на отыскании свойств материалов композитов и основывались на численном моделировании [20–23]. К молекулярно-динамическому моделированию прибегали для прогнозирования теплопроводностей композитов, обладающих наноразмерными неоднородностями [22, 23].

Широкое распространение получили исследования композиционных материалов с наполнителем в виде металлических включений. Такое внимание объясняется недостаточностью информации о теплопроводности дисперсных материалов [3, 12–15]. В работе [3] рассматривались модели Максвелла, Бруггермана, Мередита и Оделевского. При этом в [4] сделан вывод, что при практических расчётах следует отдать предпочтение модели Максвелла.

Приведём формулу Максвелла, которая часто используется для расчёта относительного коэффициента теплопроводности X в материале с определённой объёмной концентрацией ф шаровых включений [1, 3]:

λ λ 1

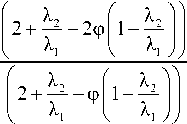
где λ и λ — коэффициенты теплопроводности матрицы и дисперсных включений.

Для сферических же включений, из анализа экспериментальных данных при относительно небольших значениях коэффициента теплопроводности их материала и диаметра, Оделевским В.И. [2] предложена следующая эмпирическая формула для вычисления эффективного коэффициента теплопроводности:

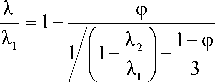
2.    Метод вычисления коэффициента теплопроводности кубического образца с дисперсным включением

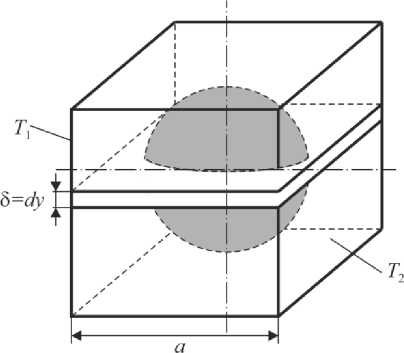
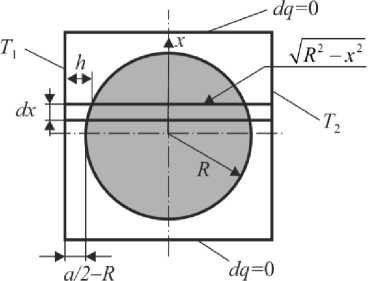
Зависимости Максвелла, Мередита и Оделевского учитывают занимаемый дисперсной фазой объём. Но необходимо предложить модель, которая будет удовлетворять всем вышеперечисленным критериям, а именно принимать в расчёт размер дисперсионных включений, их форму, пористость композита, термическое сопротивление на границе двух фаз. Для этого возьмём кубический образец с длиной ребра a , в котором расположено шаровое включение радиусом R (Рис. 1а). Коэффициент теплопроводности материала образца (матрицы) X], а Х2 — коэффициент теплопроводности дисперсного шарового включения. Боковые, верхние и нижние грани образца изолированы, чтобы пренебречь потерями. Температура левой плоскости составляет T , правой — T . Выделим из куба элементарную площадку (на рисунке 1а показана ее толщина dy ), содержащую часть включения в виде диска (см. Рис. 1б). Далее, рассмотрим только область диска, которая ограничена горизонтальным диаметром включения 2R и верхней частью линии окружности. Наконец, выделим ещё один элементарной объём из модели (см. Рис. 1в), который представляет собой призму с границами «основной материал–включение–основной материал» (Рис. 1г). На рисунке 1б представлена связанная с данной моделью декартова система координат с началом в центре включения.

Из закона Фурье для элементарного призматического объёма (Рис. 1 в ) равенство для дифференциала температуры запишем в форме, в которой фигурирует термическое сопротивление R :

dT = qdR, .

а

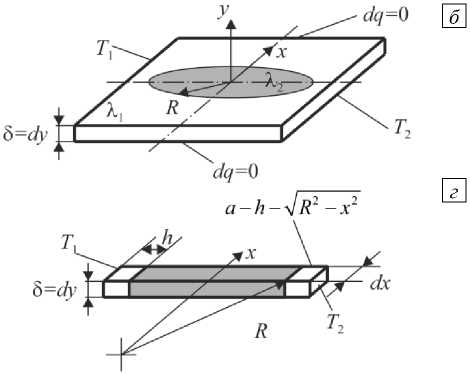
Рис. 1 . Расчётная модель: кубический образец с шаровым включением ( а ); элементарная призматическая площадка с дисковым включением, вид сбоку ( б ) и вид сверху ( в ); элементарный объём, выделенный из пластинки ( г )

в

Тогда плотность теплового потока для элементарного объёма составит:

₌__________ 71 - T 2 __________

⁴   2У R ² - x ²   a - 2У R ² - x ² '

X          X 1

Для вычисления теплового потока Q, приложенного ко всей трёхмерной модели, умножим (3) на dxdy — площадь боковых элементарных площадок, температуры на которых соответственно, равны Т₂ и T :

dQ = qdxdy .

С учётом (3) это соотношение превратиться в дифференциальное уравнение вида:

( T ^- Г ,) dxdy

2^R ² - x ² ! a - 2^R ² - x² ’

X2              Xj

после интегрирования которого найдём первообразную функцию теплового потока :

( T _- T 2 ) dxdy

^JJ 2V R ² - x ² ! a - 2V R ² - x ²

X 2               X 1

Но так как толщина пластинки известна (примем, что dy = 5 ), запишем выражение для Q в виде определённого интеграла:

R

Q = 25 J

(T - Г,) dx

2 V R ² - x²  a - 2^R ² - x² '

X 2               X 1

Взятые в интеграле пределы обусловлены тем, что учитываем две части диска: от — R до R (или от 0 до R , но домножаем на 2). После интегрирования из (4) получим формулу для вычисления коэффициента теплопроводности тонкой пластинки с дисковым включением (Рис. 1 б ):

,   ( а — 2 R ) Х ₍   Х^

Х =--+тт;---:—г а        2 (Х1 — Х2)

п —

4 а Х₂

( а Х₂ ) 2 — ( 2 R (х   л ) ) 2

arctg

а Х₂ — 2 R ( Х^Х₂ )

\] а Х ₂ + 2 R ( Х1 — Х ₂ )

Запишем (5) при условии, что диаметр d = 2 R , тогда

⁽ a ^— d ^)Х 1       ^Х 1 ^Х ₂

Х =--1--7---------Г а       2 (Х1 —Х2)

4 а Х₂ п—,        =

( а Х₂) 2 — ( d (Х, — Х₂))²

arctg

а Х₂ — d ( Х— Х₂ )

\ а Х ₂ + d ( Х 1 — Х ₂ ) ^.

Для полной картины запишем соотношение (6) с учётом объёмной концентрации, в которой вклад от дискового включения составляет

Ф = п d ² Д 4 а ² ):

Х =

arctg

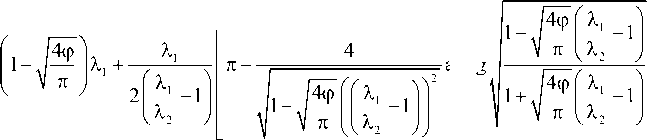
Применимость формулы (6) ограничена условием Х₂/Х[ < 0,4. При значениях отношения коэффициентов теплопроводности материалов компонентов композита, меньших 0,4, получаются мнимые значения относительного коэффициента теплопроводности. Поэтому требуется на основе численных и теоретических данных построить универсальные соотношения, которые позволят расширить интервал значений Х₂/Х₁ . Подчеркнем, что соотношения (6) и (7) применимы лишь для тонких призматических образцов с дисковым включением (Рис.1 б ).

Так как кубический образец на рисунке 1 а по сути состоит из элементарных площадок, подобных приведённой на рисунке 1 б , то необходимо просуммировать их от — R до R и учесть объёмы куба, которые не содержат включение. Тогда формула для вычисления относительного коэффициента теплопроводности кубического образца с дисперсным шаровым включением будет иметь следующий вид:

d

Х =1 1 — d к + 2 У

I а У        о

а ) ¹ у Х 1 Х 2 5

а         о а ( Х 1 —Х ₂ )

п— I

J ( Х 2 ) ²

—

4Х2

²             arctg

— ^(Х 1 ^{— Х} 2 ) )

_ а              У

^Х 2-- ^(Х 1 ^—Х 2 )

a

Х₂+ d ( Х— Х₂ ) a

, (8)

С математической точки зрения соотношение (8) следует интегрировать в пределах от 0 до d . Но при этом оно получилось бы длинным и громоздким, им было бы трудно пользоваться в практических расчетах. Поэтому, для удобства, прибегают к эмпирическим соотношениям для расчёта коэффициента теплопроводности. Так, в работе [4] вместо (6) предложено несколько возможных эмпирических формул. Для уравнения (8), включающего объёмную концентрацию дисперсных включений, подобные эмпирические выражения выводятся достаточно просто, по аналогии с формулами для (6).

3.    Численное исследование

С помощью программного комплекса ANSYS Fluent были вычислены распределения тепловых потоков и температурных полей в кубическом образце с шаровым включением (Рис. 1 а ) и плоской пластинке с дисковым включением (Рис. 1 б ). Физические условия кубического образца и пластинки полагались аналогичными: коэффициент теплопроводности материала матрицы составлял Х, = 50 Вт/(м K), коэффициент теплопроводности материала дисперсного включения Х₂ варьировался в интервале 0,4 < Х₂/Х[ < 16; боковые стенки считались изолированными, а на плоскостях, с которых распространялся тепловой поток, имели место температуры: на левой — T = 1000 K, на правой — Т₂ = 300 K.

Сначала рассматривались плоские образцы постоянной толщины 5/ a = 0,02 при различной геометрии включения: dja = 0,2; 0,5; 0,75. После получения численным путём значений распределений тепловых полей по всей длине плоского образца производилось их сравнение с результатами, установленными по аналитической зависимости (8). На рисунке 2 приведены картины распределения плотности удельного теплового потока (Рис. 2 а ) и температурное поле (Рис. 2 б ) на поверхности плоского образца с дисковым включением при Х₂/Х[ = 0,5 и d/a = 0,5 .

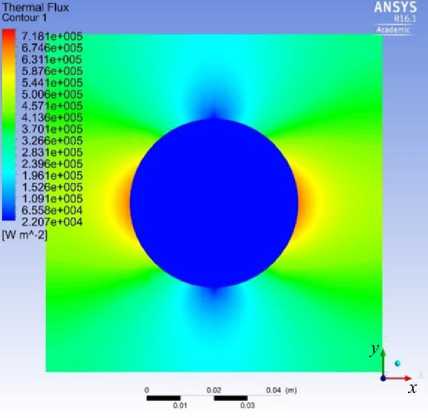
а

Рис. 2. Распределение плотности удельного теплового потока ( а ) и температурного поля ( б ) по всей поверхности пластинки при d/а = 0,5 и Х ₂ /Х 1 = 0,5

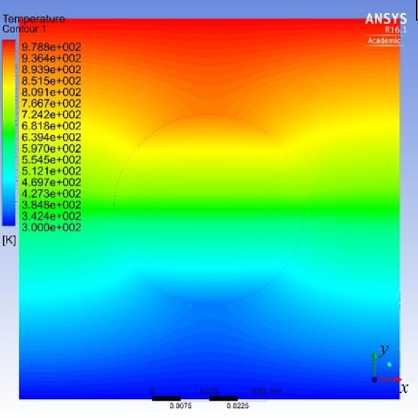
б

Распределения плотности удельного теплового потока для кубического образца с шаровым включением (трёхмерная модель, Рис. 1 а ) при двух значениях (0,2 и 15) отношения Х₂/Х[ и при d/a = 0,24; 0,5; 0,72 приведены на рисунке 3 а . Номера линий соответствуют сечениям (см. левый верхний угол), в которых авторами данной работы в пакете ANSYS Fluent проводились численные эксперименты по отысканию удельного теплового потока.

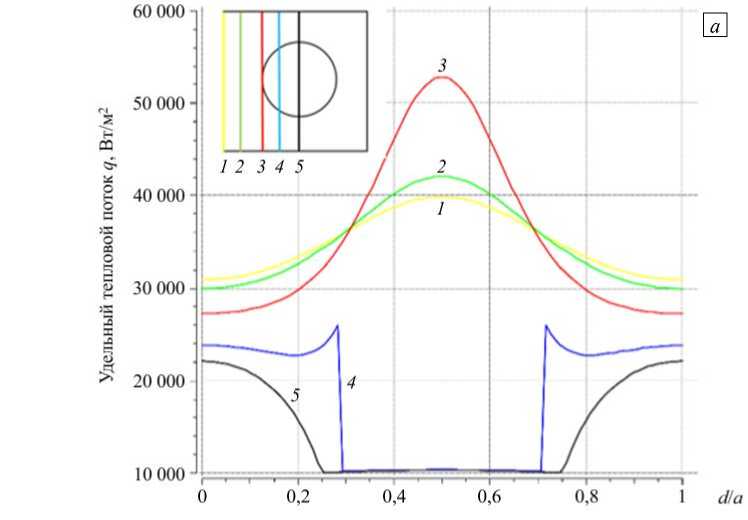
Рис. 3. Распределение плотности теплового потока по всей высоте образца в разных сечениях при d/а = 0,24; 0,72 и отношении Х₂/Х, = 0,2 ( а ), Х₂/Х, = 15 ( б )

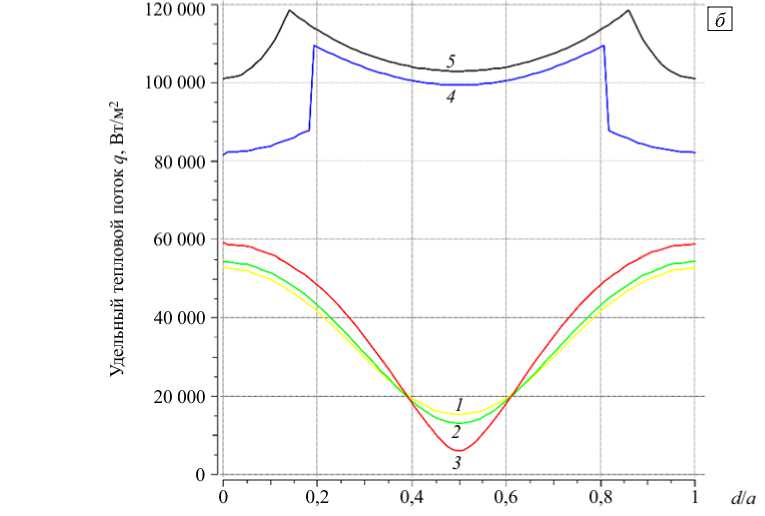
Рис. 3. Продолжение

Затем известные из расчёта в отдельных точках сечений числовые значения распределения удельного теплового потока аппроксимировались в Microsoft Excel с помощью степенных функций. В результате получались линии тренда, геометрически отображающие средние значения анализируемых показателей в соответствующем сечении. Далее, исходя из них, можно найти среднее значение удельного теплового потока q для элементарного плоского объёма, а по нему — тепловой поток Q , приложенный ко всей трёхмерной модели.

3.    Обработка данных численного эксперимента

На основании данных как численного эксперимента, так и рассчитанных по аналитическим зависимостям были построены распределения удельных тепловых потоков, которые приведены на рисунке 3. Они определены в разных сечениях по высоте образца. Для отыскания значения коэффициента теплопроводности в целом для кубического образца с шаровым включением осуществлялись следующие действия: сначала с помощью Microsoft Excel находилась усреднённая зависимость распределения удельного теплового потока в образце, затем среднее значение удельного теплового потока умножалось на высоту образца и делилось на разность действующих температур. После этого при разных значениях отношения d/а получались точки, изображенные на рисунке 4. Здесь приведены результаты лишь для двух значений отношения λλ: 10 (Рис. 4 а ) и 0,5 (Рис. 4 б ).

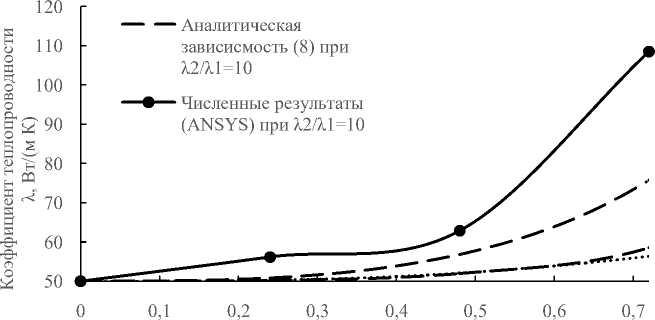
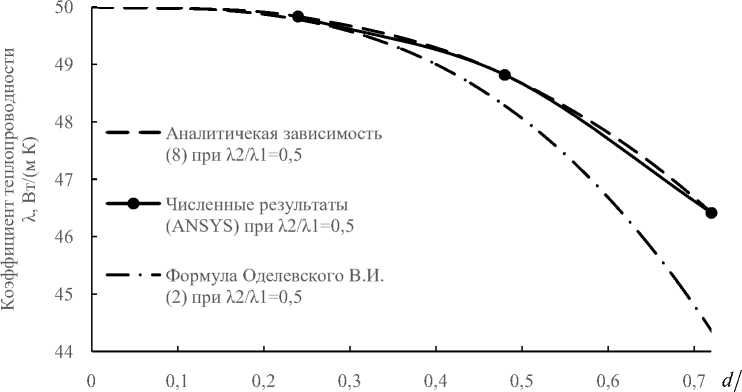
Рис. 4. Графики изменения коэффициента теплопроводности в зависимости от величины d/а при различных значениях λλ : 10 ( а ) и 0,5 ( б ); для сравнения с численными результатами представлены кривые, рассчитанные по аналитической зависимости (8), эмпирическим формулам Максвелла и Оделевского

а

d/а

а

Рис. 4. Продолжение

б

Результаты проведенного численного исследования сравнивались со значениями, найденными по формуле (8), и с зависимостями, описываемыми известными из раздела 1 формулами Оделевского (2) и Максвелла (1). На рис. 4 б зависимость Максвелла не приводится, так как она практически сливается с кривой по формуле (8).

Как сказано в [3], эмпирическая формула Оделевского, построенная на основе вычислительных экспериментов для образцов с малой концентрацией шаровых включений, может использоваться на практике и для композитов с большой концентрацией наполнителя, но при относительно небольших значениях коэффициента теплопроводности материала включений и их диаметров. Из рисунка 4 видно, что отвечающие ей кривые достаточно хорошо согласуются с другими кривыми при небольших значениях отношений dja и X ₂ /X 1 , но с ростом их величины результаты численного моделирования перестают укладываться в общую картину. Этот факт требует более детального рассмотрения. Так как данные для композитных материалов с шаровыми включениями при достаточно больших значениях ( dja >0,5 и X₂/Xj >  10) отсутствуют, то необходимо разработать метод, который бы учитывал изменение относительных параметров X ₂ /X 1 , d/a при достаточно больших значениях коэффициента теплопроводности включения и его диаметра.

Итак, при небольших значениях X₂/X[ и d/a данные, вычисленные по аналитической зависимости (8) и по предложенной в данной работе формуле, неплохо согласуются с результатами по формуле Оделевского (Рис. 4 а ). Если X₂/X[ < 1, то авторская аналитическая зависимость и формула Оделевского дают близкие, практически совпадающие, кривые. При d/a <0,5 и X₂/X₁ >1 результаты, рассчитанные как по аналитической зависимости, так и по формуле Оделевского, близки к полученным численно. При d/a >0,5 и X₂/X[ >1 наблюдается несовпадение авторских кривых ни с отвечающими формуле Оделевского, ни с вычисленными в пакете ANSYS Fluent, ни с рассчитанными по аналитической зависимости (8).

В заключение можно сказать, что при высоких значениях отношений физических ( X ₂ /X 1 ) и геометрических ( da ) параметров модели ни численный, ни аналитический подход не дают однозначных результатов. Но при этом формулы Максвелла и Оделевского, в отличие от зависимости (6) и (8), не учитывают влияние термического сопротивления на границе фаз «матрица–включение», что не совсем достоверно отображает процесс теплопередачи в таких дисперсных материалах. Следовательно, необходимо более подробно исследовать области больших значений d/a и X₂/X₁ .

4.    Выводы

Предложена простая модель определения коэффициента теплопроводности призматических образцов с дисковым включением и кубических образцов с шаровым включением. Построены соответствующие формулы для аналитического вычисления коэффициента теплопроводности, которые учитывают отношение теплопроводностей наполнителя и основного материала, а также диаметр включения. Проведено сравнение результатов, установленных по авторской формуле, с численными (полученными в пакете ANSYS Fluent) и рассчитанными по другим часто применяемым зависимостям (формулам Максвелла и Оделевского).

Выявлены недостатки — неоднозначность данных, при определении коэффициента теплопроводности композитов с дисперсным наполнителем при достаточно больших относительных значениях физических и геометрических параметров матрицы и включения, что говорит о необходимости дальнейшего совершенствования методов расчёта.

Результаты, приведённые в данной работе, могут быть использованы при проектировании различных теплозащитных композиционных материалов в авиастроении, машиностроении, металлургии и другом.