Исследование термонапряженного состояния цилиндра высокого давления паровой турбины Т - 100 - 130

При пусках паровых турбин могут возникать проблемы, связанные со значительным перепадом температур между верхней и нижней частью корпуса, между его фланцами и шпильками, с разностью удлинений вала, и корпуса, турбины и проч. В случаях, когда, перепады температур и разности удлинений превышают установленные инструкциями по запуску предельно допустимые значения, процесс пуска, необходимо прекращать. Эти проблемы наиболее характерны для ЦВД, как работающего при более высоких температурах по сравнению с другими цилиндрами турбины. На корпусе ЦВД турбины Т - 100 - 130 предусмотрено шесть штатных термопар, размещенных в пятом сечении (рис. 1) - по одной термопаре сверху, снизу, двух фланцах и двух шпильках. Для расчетов распределения температур и напряжений по длине корпуса, информация, полученная от такого количества, термопар недостаточна. Для получения более подробной информации были выполнены работы по термометрировапию внешней поверхности корпуса, и исследованию его температурного состояния в режимах запуска, и останова. В частности, были установлены термопары в семи сечениях (с первого С - 1 по седьмое С - 7 сечения), включая сечение со штатными термопарами (участки между сечениями пронумерованы римскими цифрами). Схема, размещения термопар представлена, па. рис. 1. В сечении 1 размещены три термопары: 1:1 - левый фланец, 1:2 - верх, 1:3 - правый фланец. В сечениях 2, 3, 4 - по одной термопаре: 2:1, 3:1, 4:1 в верхней части корпуса. В сечении 5 (штатное сечение) - 6 термопар: 5:1 - левый фланец; 5:2 - верх; 5:3 -правый фланец; 5:4 - левая шпилька; 5:5 - правая шпилька; 5:6 - низ. В шестом сечении - одна, термопара: 6:1 - верх. В седьмом сечении - три термопары: 7:1 - левый фланец; 7:2 - верх; 7:3 -правый фланец.

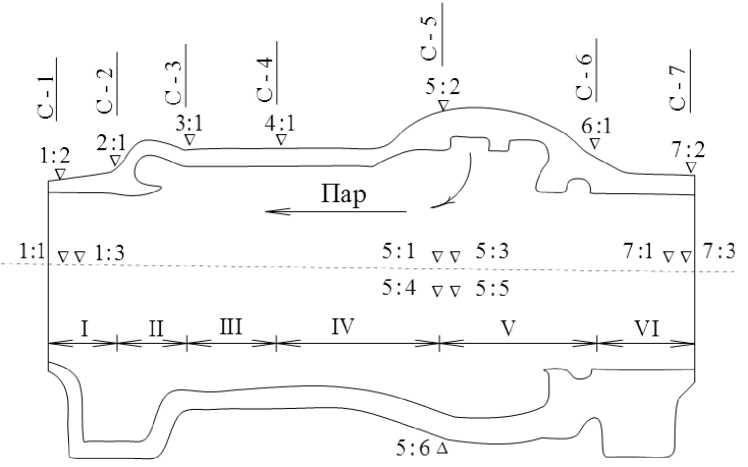
Рис. 1. Схема размещения термопар в сечениях ЦВД. С — 1, С — 2, С — 3, ...,С — 7 — сечения; 1:1, 2:1, 3:1,..., 7:3- термопары.

Термопары были установлены с целью включения их в информационно-диагностическую систему турбогенератора. Т-100-130 Самарской ТЭЦ. Система, предназначена для автоматизированного сбора, и отображения информации с использованием персональных компьютеров. К числу такой информации относятся: температура, корпуса, турбины и вала; давление и расход пара; удлинение корпуса, и вала; число оборотов вала, турбины; показатели вибрации и прочее.

Результаты экспериментальных исследований температурного состояния корпуса. ЦВД тур- бины в режиме пуска представлены на рис. 2. Из их анализа следует, что наиболее интенсивно прогреваются участки II - V. Минимальная температура в процессе пуска наблюдается в сечениях С - 1 и С - 7, то есть в той части корпуса, где находятся лабиринтовые уплотнения и скорости течения пара незначительны.

Экспериментальные значения температур были использованы для определения коэффициентов теплоотдачи, наблюдающихся при передаче теплоты от пара к корпусу, которые находились из решения обратной задачи теплопроводности. Сначала было найдено решение прямой задачи для двухслойной стенки (металлический корпус турбины - тепловая изоляция) в следующей математической постановке (рис. 3) [1, 2]:

ЭТ)(х, 7) = Э2Т) (х, /у Э7         г Эх2    ’	(7 > 0’   х^-i < х < хд г = 1,2; хо = 0’   х2 = 5);      (1)
Т (х, 0) = То,   (г = 1’ 2)	(2)          А1    эх    + ai[Tcpi   Т1(0, 7)] = 0;        (з)
Т1(х1,7) = Т2(х1, 7);	(4)           А. Э              А2          '                    (5)

А2---Эх—” + а2 [Т2 (5, 7) - Tcp2] = °’ где Т - температура г-го слоя (г = 1, 2); х - координата; 7 - время; 5 = 51 + 52 - суммарная толщина двухслойной стенки; А), а - коэффициенты теплопроводности и температуропроводности г-го слоя (г = 1, 2); То - начальная температура; оц - коэффициент теплоотдачи со стороны пара; а.2 - коэффициент теплоотдачи с о стороны окружающей среды; Tcpi - темпера тура пара; Tcp2 -температура окружающей среды.

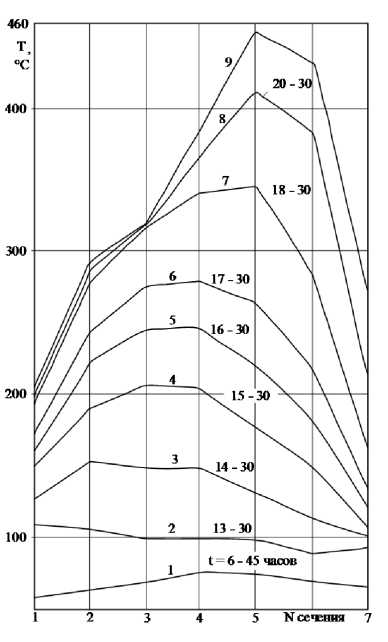
Рис. 2. Распределение температуры в верхней части ЦВД в процессе запуска (кривые 1 - 8); 9 - стационарное состояние; t - время.

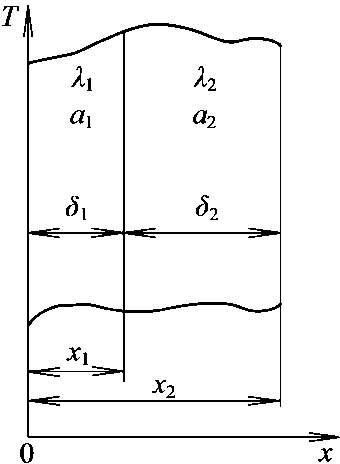
Рис. 3. Схема двухслойной конструкции.

Введем следующие безразмерные переменные и параметры:

0,      Т ; ; 6 = |; Fo = .); Bii

(То - Тс_Р2)         5          5²

а15

A1 ’

тэ: _ «25 Bi2 = Щ—,

A2

АТ =

^{( Т}ср 1 - ^Тср2) (То - Т_СР2)

где 0, - безразмерна я температура (г = 1, 2); Fo - число Фурье (без размерное время); 6 - безразмерная координата; Bi₁, Bi₂ - числа Био; а - наименьший из коэффициентов температуропроводности а,, (г = 1, 2).

С учетом введенных обозначений задача. (1) - (6) принимает вид

де(6, Fo)    а , д2е(6, Fo) dFo   = а    d62   ,    (Fo > 0	6,-1 <6<6,;   г = 1, 2;   6о = 0;   62 = 1);     (7)
е,(6, 0) = 1,   (г = 1, 2);               (8)	d 0 1 (0; Fo) + Bi1 [АТ - 01 (0, Fo)] = 0;       (9) d6
01(61, Fo) = 02(61, Fo);               (10)	601(61, Fo)       d02(61, Fo) A1     d6     = A2     d6     ;

^{9 0 2 (1 Fo)} + Bi2e2(1, Fo) = 0,                                (12)

д6

где соотношения (10), (11) представляют условия сопряжения, записанные в виде равенства, температур и тепловых потоков в точке контакта слоев 6 = 61-

Решение задачи (7) - (12) принимается в виде

0,(6, Fo) = Ф,(6) + 77,(6, Fo),   (г = 1, 2),                                (13)

где функция Ф, (6) является решением стационарной задачи с неоднородными граничными условиями, а функция 7 , (6, Fo) - решением нестационарной задачи с однородными граничными условиями.

Математическая постановка задачи для функции Ф, (6) имеет вид

-^^ = 0,  (6,-1 <6<6,;  г = 1, 2;  6о = 0; 62 = 1),(14)

^6° +Bi1[АТ - Ф1(0)]=0;         (15)           Ф1 (61) = Ф2(61),(Ю)

A1 -^ = A2 -^            (17)             ■(18)

Решение задачи (14) - (18) принимается в виде

Ф,(6) = А, + D,6,     (г = 1, 2),(19)

где А,, D, - неизвестные коэффициенты.

Очевидно, что соотношение (19) удовлетворяет уравнению (14). Неизвестные А,, D,, (г = 1, 2) находятся из граничных условий (15) - (18). Подставляя (19) в (15) - (18), для их определения будем иметь систему четырех алгебраических линейных уравнений, из решения которой находим

А1 = Bi1АТ(Bi261(A2 - A1) + A1 (1 + Bi2))/r;             А2 = Bi1АТ A1 (1 + Bi2)/r

D1 = -Bi1АТBi2(A2/r) ;                                D2 = -А^фАТ(Bi2/r),      (20)

где r = A1Bi1 (1 - Bi2(61 - 1)) + Bi2A2(1 + 61Bi1).

Математическая постановка задачи для функции 77,(6, Fo) имеет вид

.   '    .    ,'", (Fo > 0; 6.-1 <«6; • =1,2; 6о = 0; Ь = 1);    (2)

,,«, 0) = 1; (г = 1, 2)           (22)            ^^1^^Fo) - Bii,i(0, Fo) = 0;(23)

,1(6„ Fo) = ,вй, Fo);           (24)        Ai" = A2^'^^o1;

d6 d6

^1 Fo) +Bi2,2(1, Fo) = 0.(26)

d6

Решение задачи (21) - (26), следуя методу JI.В. Канторовича, принимается в виде

,,(6, Fo) = f(Fo>,(6),      (г = 1, 2),(27)

где f(Fo) - неизвестная функция времени; ^,(6) - координатные функции (г = 1, 2), определяемые так, чтобы решение (27) удовлетворяло граничным условиям (23), (26) и условиям сопряжения (24), (25).

Сначала, находится координатная функция для второго слоя, которая принимается в виде

^2(6)= Я — 62,

где R - неизвестная постоянная, определяемая из граничного условия (26). Подставляя (27) (с учетом (28)) в (26), относительно неизвестной R будем иметь алгебраическое уравнение, из решения которого находим R = (Bi₂ + 2)/Bi₂. Учитывая найденное R, соотношение (28) будет

^(£) = (Bi2 + 2)/Bi2 - 62.

Координатная функция для первого слоя принимается в виде

У1(6) = Г + F16 + F2 62, где F, F1, F2 - неизвестные постоянные, определяемые из граничного условия (23) и условий сопряжения (24), (25).

Подставляя (27) (с учетом (29)) в (23)-(25), относительно F, F1, F2 будем иметь систему трех алгебраических уравнений, из решения которой находим

F = 2 г 2 /г 1 ; Fi = BiiF ; F2 = - (2A261 + BiiAiN + Bii62(2A₂ — Ai)) /(^161),      (31)

где п = Ai(2 + Bii6i): Г2 = AiN - 62(Ai - A2): N = (Bi2 + 2)/Bi2.

Подставляя найденные значения F, F1, F2 в (30), получаем

^1(6) = 2Г2/Г1 + B11F6 - 62 (2A261 + BiiAiN + Bii62(2A2 - Ai)) /(^61).          (32)

Соотношение (27) с учетом найденных соотношений для координатных функций ^1(6) и ^2(6) точно удовлетворяет условиям (23) - (26). Для определения неизвестной функции времени /(Fo) потребуем, чтобы соотношение (27) удовлетворяло не уравнению (21), а. некоторому осредненному уравнению, то есть интегралу теплового баланса.

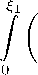
d,i(6, Fo) d Fo

h i d²,i(6, Fo) А ¹ /5,2(6, Fo) a    d6^{2       6} J V   dFo

a2 d²,2(6, Fo) A a d6²

d6 = 0.

Подставляя (27) в (33), находим

/ f ^df ai d2pi A        Г f ^df °2 ^d2^₂ A

J (dFo^¹ - V^/^6^J^{d6 +} J (dFo^² - T^/16^ry^d6 = ^0.

0                                            51

Определяя интегралы в (34), относительно неизвестной функции f(Fo) получаем следующее обыкновенное дифференциальное уравнение df

' dFO+    = 0, где p.i = (2CiAiBi2 (3 + 3C2 - № - C3Bii) + 12CiAi + 4Ci%Bi2 + 4ф2ВфА1) / (3p3) + (2 - 3Ci + + C3)/3 + 2(1 - Ci)/Bi2; р2 = (4aiBi2^iA2(1 + CiBii) + 2aiBiiAiBi2(1 - C2) + 2aiAiBii)/(ato) + + 2d2(1 - Ci)/a; P3 = Bi2A1(2 + £iBii).

Интегрируя уравнение (35), получаем f (Fo) = C1 exp

⁶⁽A<4 ⁺ P5 ⁺ P8 ^{+ 2Bi}2d2^Ai^(Ci ^- 1) ^{- 2Bi}idi^Ai⁾ M6 + Bi2C2Ai(Bii + Ci) - 4Bi2C3A2 + M9 - M7

Fo) ,

где Ci - константа, интегрирования: ^4 = Bi_iBi₂C2a_i(A_i - A2); ^5 = Bi_iBi2C_ia2A_i(C_i - 1); ^6 = = Bi_xBi2C4(Ai - A2); P7 = Ai(6BiiCi - 4Bii - 12); p8 = Bi^a^Ai - 2A2); _№ = 2Bii^Ai(Ci - Bi2).

Подставляя (19), (27) в (13), находим

@i(C,Fo) = n, + AC + f(Fo>,(C),   (г = 1, 2).

Для определения константы интегрирования Ci используется начальное условие (8). Составляя интеграл его невязки, находим

41i

У (ОДС, 0) - 1) dC + У <©2(C, 0) - 1) dC = 0.

Подставляя (37) в (38), получаем

/ «Ах + ПЮ + f (0)yi(C)>df + / ((A2 + O2C) - f(0)^0 dC = 0.139:

Определяя интегралы в (39), относительно константы интегрирования Ci будем иметь алгебраическое линейное уравнение, из решения которого находим

Ci

3 (г₃ - г ₄ - Bi₁ATA_i(2 + Bi₂) + 2Bi_iA_i(Bi2 + 1) - 2A2Bi2)(2 + C_iBi₁)A_iBi2

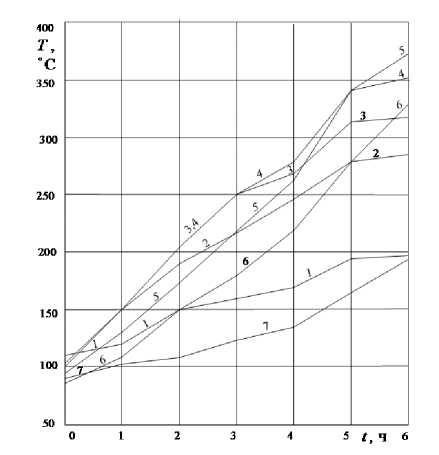
Рис. 4. Изменение температуры во времени в верхней части корпуса турбины. 1 - 7 - номера сечений (см. рис. 1).

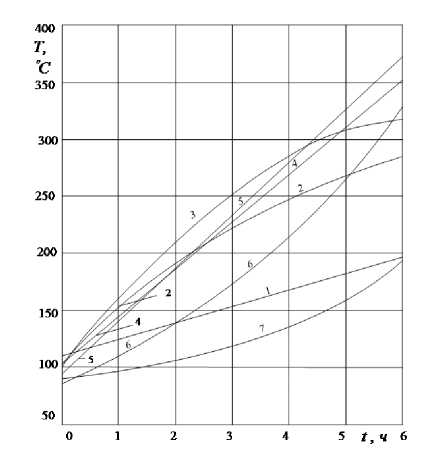
Рис. 5. Результаты аппроксимации температуры (см. рис. 4) по формулам (41).

времени запуска, от 13 - 30 до 20 - 30 часов эти можно приближенно аппроксимировать линейной зависимостью от времени (кривые 1, 4, 5) и квадратичной (кривые 2, 3, 6, 7)

Т (t) = vi + v₂t;       Т (t) = vi + v2t + из! ² ,                          (41)

где v1, v₂, V3 - коэффициенты аппроксимации. Их значения для каждой кривой даны в таблице 1. Кривые, полученные по формулам (41), даны па. рис. 5.

Соотношения (41) путем решения обратной задачи теплопроводности были использованы для определения коэффициентов теплоотдачи (од) на внутренней поверхности стенки турбины [4]. Применительно к задаче (4) - (9) формулами (41) определяется температура, в точке контакта слоев х = х1, то есть Т (х, t) = Т (х1, t).

Подставляя соотношения (41), представленные в безразмерном виде, в левую часть решения (37), относительно Bi1 = а15/А1 для каждого сечения получаем трансцендентное уравнение, из решения которого находим Bi1, а, следовательно, и коэффициент теплоотдачи а1. Используя решение (37) и соотношения (41), были найдены средние за. время запуска, коэффициенты теплоотдачи со стороны пара, в тех точках верхней части корпуса. ЦВД, где были установлены термопары. Их величины соответственно со второго по седьмое сечения оказались следующими: 12, 20, 36, 35, 11 Вт/(м² • К ). Анализ полученных результатов позволяет заключить, что наименьшая величина о-| наблюдается в тех сечениях, где находятся лабиринтовые уплотнения, в пространстве между которыми скорости движения пара невелики (застойные зоны). Максимальные о-| имеют место там, где наблюдаются высокие значения температур и скоростей течения пара.

Найденные значения коэффициентов теплоотдачи позволили определить распределение температуры по толщине стенки и тепловой изоляции для сечений 1, 2, 4, 5. Результаты расчетов по формуле (37) (представленной в размерном виде) приведены на. графиках рис. 6. Их анализ позволяет заключить, что наибольший перепад температуры по толщине стенки, составляющий 8.2°C. наблюдается в пятом сечении. то ость там. где толщина, стопки максимальная (51 = 0, 08m).

Исходные данные для решения задачи были следующие:

А1 = 37 Вт/(м • К ); А2 = 0, 8 Вт/(м • К ); а1 = 0, 8 • 10^-5 м²/с; а₂ = 0, 8 • 10^-6 м²/с; 52 = = 0, 3м; а₂ = 10 Вт/(м² • К ); t_cp = 30 °C.

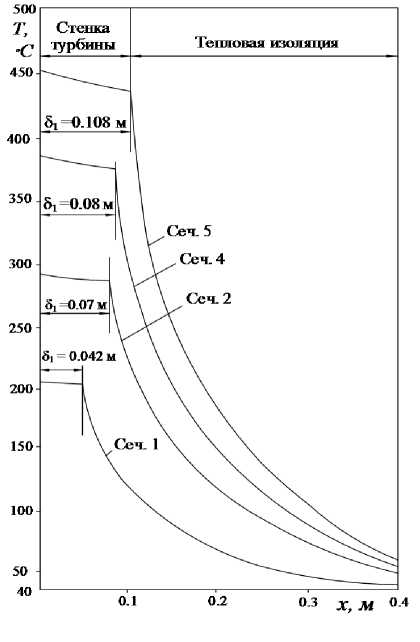
Рис. 6. Графики изменения температуры по толщине двухслойной (металл - тепловая изоляция) стенки ЦВД турбины в различных сечениях по длине корпуса (см. рис. 2).

Таблица 1. Коэффициенты аппроксимации экспериментальных значений температуры.

Коэффициенты аппроксимации	Номер сечения корпуса, турбины (см. рис. 1)
	1	2	3	4	5	6	7
V1	110	105	100	100	94	85	90
V2	14	44.83	63.33	42.17	46.7	23.17	4.37
v3		- 2.5	- 4.44			2.83	2.1

Отметим, что толщина, металлической части стенки в разных сечениях корпуса, была, разной и, в частности, сечение 1: 51 = 0, 042 м', сечение 2: 51 = 0, 07 м', сечение 4: 51 = 0, 08 м', сечение 5: 51 = 0,108 .м (рис. С).

Результаты экспериментальных исследований температурного состояния корпуса. ЦВД турбины Т-100-130, приведенные на. рис. 2, были использованы для расчетов температурных напряжений и перемещений. Для этого использовался метод конечных элементов [5].

Математическая постановка, задачи термоупругости имеет вид

^ + ^ = 0; ^ + Э!,,       (42) дх    ду      ду    дх де. + Of, = 022., ду2   дх2 дхду             J е. = - (,x — va,) + атТ;        е, = -1 (,y - a.) + атТ; е. = ди/дх;                    е, = дУ/ду; 2(1 + v) т., =   Е   т.у;       24) 2., = дУ/дх + ди/ду,   (45) где ст., цу - нормальные напряжения; тжу - касательное напряжение; е., еу, у., - деформации; U,

V - перемещения; а т - коэффициент липейного расширения; Е - модуль упругости; v - коэффициент Пуассона, х,у - координаты.

Граничные условия задаются в виде отсутствия напряжений на. границе в направлении, перпендикулярном касательной в данной точке. Также, задается условие отсутствия перемещений какой-либо точки по всем координатным осям (чтобы исключить движение тела, как целого)и отсутствие перемещений в какой-либо другой точке по одной из координат (для исключения вращения тела).

Схема, автоматического разбиения поперечного сечения ЦВД турбины представлена, па. рис. 7. Автоматическое разбиение выполнялось лишь по предварительной информации о координатах х,у граничных точек области. В результате разбиения получены 123 узловые точки и 160 треугольных элементов.

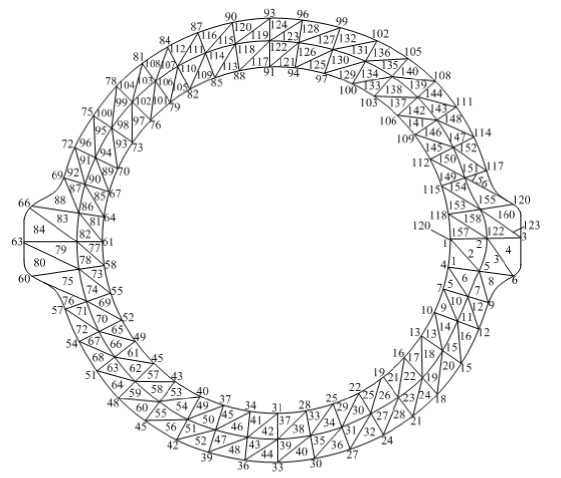
Рис. 7. Схема автоматического разбиения области па треугольные элементы.Число узловых точек - 123; число элементов - 160.

Температурное поле в сечении турбины (пятое сечение, см. рис. 2) и результаты расчета, перемещений представлены па. рис. 8. Анализируя температурное поле, наблюдавшееся в 15 - 45 часов запуска, (см. рис. 2) можно заметить значительную разность температур между верхом-низом и фланцами (до 80 ° С). В то же время температуры верха и низа практически совпадают. Незначительно отличаются также и температуры фланцев (At = 2°С).

Проведем анализ температурных перемещений корпуса. Так как температурное поле практически симметрично относительно верха, и низа, и фланцев, то поле перемещений также оказывается практически симметричным (см. рис. 8). Однако ввиду существенной разницы температур между верхом-низом и фланцами, в зоне больших температур (па. фланцах) перемещения оказываются большими (до 0, 9 мм), в связи с чем, на фланцах образуются вздутия корпуса. Подобная несиммет-рия деформации корпуса, может приводить к аварийным ситуациям (раскрытия корпуса, в области фланцев, задевания венца, лопаток о корпус, появление трещин на. корпусе и проч.).

На рис. 9 представлены результаты расчетов температурных напряжений а_х. Их анализ позволяет заключить, что уровень напряжений относительно невысок (не более 8 кг/ мм²). Причем на. внутренней поверхности, как более нагретой, развиваются напряжения сжатия, а. на. внешней растяжения.

В пределах отдельных участков корпус ЦВД, пренебрегая фланцами, можно приближенно представить как полый цилиндр, а. температурное поле считать осесимметричным. В этом случае

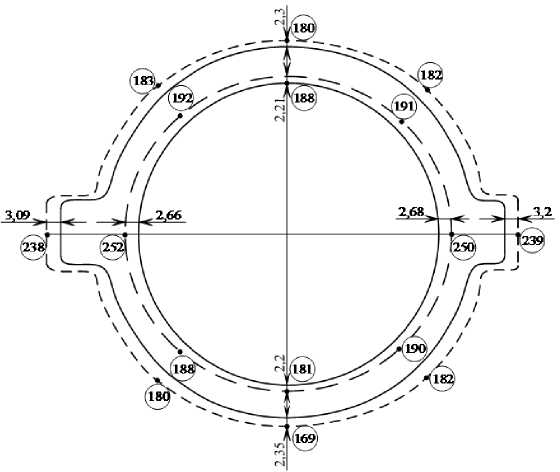
Рис. 8. Деформация сечения корпуса от действия температурных сил в режиме пуска. Сплошные липни - размеры сечения в пепагретом состоянии турбины. Штриховые линии - деформация сечения от температурного расширения. Цифры па стрелках - удлинения корпуса в мм. Цифры, обведенные кругом, - температуры в °C.

для расчета, температурных напряжений применяются следующие формулы [6]

О г

аЕ 1

1 — V r ²

¹ II

1 в

У Trdr гЪ

о© =

аЕ 1

1 — V r2

г„

г

O z

¹ II

¹ в

г

∫︁

Trdr

j Trdr + У Trdr

г^

г

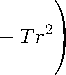
аЕ

1 — V

г

У Trdr

г

Т

где ст_г, о©, a_z - соответственно радиальное, о кружное и осевое напряжения: r_B, r_H - соответственно внутренний и наружный радиусы полого цилиндра.

Температура Т принималась по толщине стенки в виде следующей линейной функции

Т = Ai + A2r, где A1, A2 - коэффициенты аппроксимации, определяемые на основе экспериментальных и расчетных данных по температуре па. внутренней и внешней поверхностях стенки.

Из физических соображений и, как это следует из формулы (46), радиальные температурные напряжения о_г пр и r = r_B и r = r_H равны нулю. Радиальные напряжения внутри стенки не превышают 1-3 кг/мм 2. В связи с чем, в дальнейшем их не будем рассматривать. Максимальных значений (до 15 кг/мм²) напряжения о© достигают на внутренней поверхности стенки (напряжения сжатия). По толщине стенки напряжения меняют свой знак и на. внешней поверхности наблюдаются окружные напряжения растяжения до 7 кг/мм² (см. рис. 9).

Сравнивая результаты этих расчетов с результатами, полученными с помощью метода конечных элементов (см. рис. 9), можно заметить, что в верхней и нижней части сечения напряжения о© незначительно отличаются от напряжения а_х. Отмстим, что напряжения о_х в этих областях, при расчетах методом конечных элементов по сути, являются окружными напряжениями.

Осевые напряжения ст, также изменяют свой знак в пределах толщины стенки от -12 кг/ мм² на внутренней поверхности до +4 кг/ мм² на внешней поверхности (см. рис. 10).

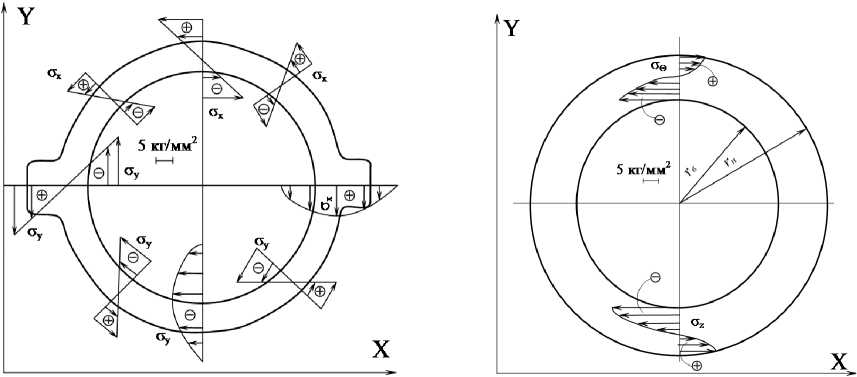
Рис. 9. Эпюры распределения напряжений а_х в плоскости поперечного сечения корпуса турбины Т-100-130 в режиме запуска, ф - растяжение; ф - сжатие. Температурное поле представлено па рис. 8.

Рис. 10. Эпюры распределения окружных се и осевых z температурных напряжений в сечении корпуса ЦВД турбины Т-100-130, ф - растяжение; ф - сжатие.

Кроме температурных сил, на. материал корпуса, действуют еще силы давления пара. (130 атм.), находящегося внутри корпуса. Приводимая далее методика, позволяет выполнить расчет напряжений и перемещений цилиндров, находящихся под действием постоянных по длине наружным и внутренним давлением [8]. По формулам этой методики можно выполнять расчет и тогда, когда, давление распределено только па. части длины или, когда, концы цилиндра, закреплены. В данном случае напряжения можно определять лишь в сечениях, достаточно удаленных от торцов.

Применительно к корпусу турбины приводимые ниже формулы будут справедливы лишь для центральной ее части. Вследствие осевой симметрии нагрузки, напряжения и деформации будут симметричны относительно оси цилиндра, и постоянны по его длине.

Формулы для определения напряжений имеют вид [7]

Т_вг2_-РГ2 + (Р_в - Р_н)r2r2 .

Г2 — _г2        ('2 — г2)р² ’

^ст '

Р_вт2 - Р_нг² - (Р_в - Р_н)г2Г2 .

Г2 - _г2        ('2 - _т2)р² ’

ст

Р в' в

^п' II

'll 'в

где ст' - нормальное радиальное напряжение: ст/ - окружное тангенциальное напряжение: ст' -осевое напряжение; Р_в, Р_н - внутреннее и наружное давление; r_B, r„ - внутренний и наружный радиусы; р - текущий радиус (рис. 10).

Исходные данные для расчета:

Р_в = 130 кг 'слР: Р_п = 1 а "г 2:лР: r_B= G33 лиг. r_n= 710 AtAt: ц= 0.3; Е= 18000 кг аки².

Радиальные напряжения ст' внутри и снаружи принимают соответственно значения ст'в = = -130 кг/см2 = -1, 3 кг/мм2; ст'н = -1 кг/см2 = 0,01 кг/мм2. Таким образом, найденные по формуле (50) напряжения на. внутренней и внешней поверхностях, совпадают с заданными на. этих поверхностях давлениями. Знаки напряжений отрицательные (сжатие).

Окружное напряжение ст/, найденное по соотношению (49), для внутренней и наружной поверхности цилиндра принимает следующие значения ст/в = 10, 6 кг/мм2; ст/н= 8,9 кг/мм2. Знаки напряжений положительные (растяжение). Графики распределения напряжений, найденных по формулам (49), (51), а. также суммарных напряжений, возникающих от сил давления пара, и температурных сил, приведены на. рис. 11.

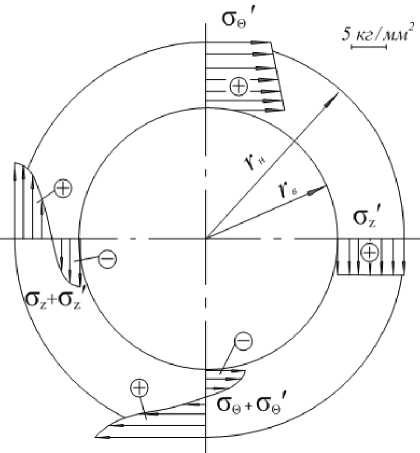
Рис. 11. Эпюры распределения напряжения оф, оу, возникающие от сил давления пара, и суммарных напряжений (температурных и от сил давления пара), оу + оф, од + оф

Осевое напряжение сг‘,=4,98 кг/мм2, найденное по формуле (51), имеет одинаковое значение по толщине стенки цилиндра, и оказывается положительным (растяжение).

Анализируя полученные результаты, заключаем, что па. внутренней поверхности корпуса, окружные напряжения уф от температурных сил и сил давления пара, незначительно отличаясь по абсолютной величине, имеют противоположные знаки. Таким образом, внутренняя поверхность оказывается практически разгруженной от окружных напряжений. Знаки окружных температурных напряжений и напряжений от сил давления пара. па. внешней поверхности корпуса, оказываются одинаковыми и, следовательно, они суммируются. В результате суммарные окружные напряжения растяжения на внешней поверхности достигают порядка 17,6 кг/мм2.

Заключение

• 1.    Используя экспериментально-теоретические исследования температурного состояния корпуса. ЦВД турбины Т - 100 - 130 в процессе ее запуска, по известной из эксперимента, температуре внешней поверхности металлической части корпуса, из решения обратной задачи теплопроводности найдены средние за. период запуска, коэффициенты теплоотдачи па. его внутренней поверхности.

• 2.    Используя найденные из решения обратной задачи теплопроводности коэффициенты теплоотдачи, получены кривые изменения температуры в различных сечениях корпуса. ЦВД с учетом тепловой изоляции па. внешней поверхности стенки, которые были использованы для определения температурных напряжений.