Исследование точности оценки систематических ошибок по азимуту для системы РЛС

Несмотря на развитие новых методов навигации, в авиации главным остается наблюдение за воздушными судами (ВС) с помощью радиолокационных станций (РЛС). РЛС как измерительный прибор имеет погрешности наблюдения, в том числе систематические. Наибольшие проблемы для использования РЛС-информации доставляет систематическая ошибка РЛС по азимуту. Ее оценивание является важной задачей.

В гражданской авиации применяются трассовые радиолокаторы, работающие на больших расстояниях, и обычным является наблюдение за движением одного ВС одновременно несколькими РЛС. Для этих РЛС возможно оценивание систематических ошибок по азимуту на основе данных совместного наблюдения [1]. При этом используется то обстоятельство, что направление действия систематической ошибки по азимуту у каждой РЛС свое.

В работе изучается вопрос о зависимости точности оценивания систематических ошибок по азимуту от взаимного расположения системы РЛС и наблюдаемого участка траектории ВС. В различных предположениях о движении ВС и условиях наблюдения, а также для различных алгоритмов оценивания такая зависимость может быть разной. Исследование проводится для ≪ эталонной ≫ задачи с наиболее простой ситуацией наблюдения, при этом берется наиболее простой алгоритм оценивания, оптимальный в смысле математического ожидания квадрата отклонения. Полученные результаты могут служить ориентиром и для других алгоритмов, минимизирующих этот критерий.

2.    Модель наблюдения

Будем изображать все РЛС, движущееся ВС и отметки замеров на плоскости Π ≃ R ² . Например, это может быть плоскость, касательная к поверхности Земли в некоторой точке.

Все объекты на плоскости П получаются проектированием (некоторым заданным способом) на нее пространственных объектов.

Радиолокаторы в дискретные моменты времени измеряют дальность до ВС и азимут (угол между направлением на ВС и направлением на север). Предполагаем, что в каждый момент t i измерения производит только одна РЛС. Общее количество моментов измерений обозначим символом n (т.е. i меняется от 1 до n), количество моментов измерения k-й РЛС — символом n _k . Пусть m — число всех РЛС (k меняется от 1 до m). Номер наблюдающей РЛС задается известной функцией от номера измерения: k = k(i).

Обозначим вектор истинного положения ВС на плоскости П в момент времени t i символом x i , а отметку замера — z i . Предполагаем, что отметка замера откладывается на П от точки радиолокатора по измеренной дальности и азимуту.

В каждой точке x плоскости П введем единичный вектор e r k (x) Е R ² направления от k-й РЛС в данную точку. Этот вектор указывает направление действия ошибки по дальности. Также введем вектор e _f k (x) Е R ² , ортогональный вектору e r k (x), получающийся из e r k (x) правым поворотом. Такой вектор связан с направлением действия ошибок по азимуту. Расстояние от точки x до k-й РЛС обозначим символом r k (x).

Ошибки РЛС имеют различную природу и свойства. В ходе процесса радиолокации (передача и прием радиоволн, детектирование сигнала) для каждого момента t i возникают ошибки измерения дальности w _i ^r и азимута w _i ^ϕ с хорошими статистическими свойствами:

w i

А

^w i^r

ϕ i

E { w i } =

E {w i wT} = O 2 4

О О

О о

r 2

S k(i) 4 E { w i w T } =    kto

О

ϕ 2 ° k(i)

,

V i, j Е 1,n, i = j.

Среднеквадратичные отклонения по дальности и азимуту зависят от того, какой радиолокатор производит наблюдение в момент t i .

Существуют и другие ошибки, обусловленные искажениями при обработке информации, механическими сбоями и износом РЛС. Они уже не имеют хороших статистических свойств. Среди них наибольшее значение имеют систематические ошибки РЛС по азимуту X k , к Е 1, m. Введем обозначение X = [X 1 ... X _m ] ^T Е R m .

В принятых обозначениях уравнение наблюдения, связывающее измерение с истинным положением, запишется следующим образом:

z i = x i + e rk(i) ^(x i ) w r + e f^i/ x i ) r k(i) ^{( x} i ⁾ ( ^X k(i) + ^{w f} ) .                      ⁽²⁾

Отметим, что уравнение (2) нелинейно.

Если мы хотим ввести понятие точности оценивания величин λ k в зависимости от взаимного геометрического положения ВС и всех РЛС, разумно рассматривать наблюдения за небольшими участками траекторий ВС, на которых расстояния r k до всех РЛС и направления e _rk ≪ точка — РЛС ≫ (а также жестко с ними связанные векторы e ϕk ) значительно не изменяются, и, в первом приближении, соответствуют некоторой точке x * Е П. Область вокруг точки x _∗ , где выполняются указанные предположения, можно определить, например, как все x Е П, для которых выполняются следующие неравенства с некоторыми малыми константами K i и K 2

| r k (x) - r k (x * ) | r k (x * )

< K i , | e rk (x)

- e rk (x * ) | <  K 2 , | e ^k (x) - e ^k (x * ) | <  K 2 ,

V k Е 1, m.

В этой области разумно перейти к уравнению с ≪ замороженными коэффициентами ≫ , зафиксировав значение аргумента x в функциях e rk (x), e ^k (x), r k (x) и сделав его равным x * :

Z i = x i + e rk (x * ) w r + e fk(i) (x * ) r k(i) (x * ) ( X^ ) + w ^f ) .                    (3)

Уравнение (3) также можно получить, производя линеаризацию соотношения (2) по переменным X i , А в окрестности точки x i = x * , Л = 0.

Для постановки задачи оценивания недостаточно знать уравнение (2) или даже (3) — требуется задать закон изменения переменной x i по времени.

Гражданские ВС на значительных участках своего полета выдерживают прямолинейное равномерное движение. Кроме того, известно, что гражданский самолет — массивный объект. Поэтому при рассмотрении малой области наблюдения и короткого участка траектории разумно предполагать движение настолько близким к прямолинейному равномерному:

Xi = X0 + Vo (ti - to) , что погрешностями этого приближения можно пренебречь. В уравнении (4) величины Xo, Vo E R2 — неизвестные положение и скорость на некоторый заданный момент времени t0 .

Введем вектор-столбец 9 E R ⁴ , включающий в себя неизвестные параметры x o , V o прямолинейного равномерного движения и матрицу преобразования A(t):

⁹ =[xo]'    ^{A ( t )} = [

1 0 t

0 1

-

t o

0t

- t o

]

.

Уравнение движения (4) запишется в виде

X i = A(t i ) 9 .

Обозначим символами C ik (x), D k (x) следующие матрицы:

C ik (x) = [ A(t i )

0 • 0	0 •  • 0	r k (x)e ^k (x)	0 • 0	0 • 0
5	k+3	k+4	k+5	4+m

, erk(x) rk(x)e^k(x) ] .

D k (x) = [

В матрице C ik (x) в части, стоящей справа от элементов матрицы A(t i ), ненулевым является лишь столбец с номером к +4 (номера столбцов подписаны снизу матрицы).

Вводя вектор-столбец всех неизвестных y = [ 9 T A T ] T и используя матрицы, указанные выше, а также предположение о движении в виде уравнения (5), получим матричный вид уравнения наблюдения (3):

Z i = C i k(i) (x * ) у + D k(i) (x * ) W i .

3.    Задача оценивания

Задача оценивания неизвестного вектора-столбца у состоит в построении функции у (зависящей только от измерений { z i } n ₌₁ ), близкой к у в заданном смысле. Для линейного уравнения наблюдения (7) со случайными ошибками w i , удовлетворяющими (1), известен классический результат: минимум критерия

Jy ^ E {||у - yh2} в классе линейных несмещенных оценок достигается на оценке обобщенного метода наи- меньших квадратов [2]. Формулы оценки имеют вид

P ^-1

ⁿ                          - 1                  ⁿ

= EcT k(i) D k ^V D ¹       C ik(i) , у = PEc i T k(i) (D k(i) ^ k(i) D T (i ))

i=1                                                 i=1

z i .      (8)

Матрица P является матрицей ковариации ошибок оценивания: P = E { (y — y)(y — y) T } . В формуле (8) для простоты записи не указана зависимость матриц C _{i k} , D _k (а как следствие, и P) от переменной x ∗ . Будем опускать символ такой зависимости в случаях, когда речь идет о значениях при фиксированном x _∗ .

Известным фактом является то, что часть координат столбца y, например λ, оптимально приближается в смысле минимума критерия J a = E {|| A — A h 2 } частью A координат столбца y = [0 T A T ] T . То же самое можно сказать и об оценивании конкретной величины λ k : компонента λ k столбца λ минимизирует отклонение от истинного значения λ k в смысле критерия J \k = E {| A k — A k | ² } . Также известна связь между значениями критериев J y , J a , J λ k и матрицей ковариации:

J y = E { h y — A h ² } = tr { P } , J a = E {|| A — A h ² } = tr { P _AA } ,

J xk = E {|A k — A k | ²} = P _xx,kk . (9)

Здесь P aa = E { (A — A)(A — A) T } — блочная часть матрицы P , соответствующая части A переменной y , а P λ λ_, k k — k-ая компонента ее главной диагонали. Вообще, в нашей задаче, связанной с оцениванием части координат, матрицы P и P ^-1 удобно представлять в блочном виде:

^P θθ ^P θλ

P λθ P λλ

- 1 ^P θθ ^P θλ

P = P a, P aa '

При этом для подматриц справедливы соотношения

P eA = P T ,   P ee = P T , ,   P aa = P T ,  P eA = P T ,   P ee = P T , ,   P aa = P T -

Матрицу Pλλ можно получить, не обращая матрицу P-1 целиком. Известно [2] соотно- шение

P

= ^P - 1 + ^P - 1 P A 9

/                        -1

(P ee — P 9 A P - 1 P A 9)    P e A P TA¹ .

Выражение (10) также полезно и для анализа структуры P , поскольку блоки P θ θ , P θ , P связаны с блоками матриц C _{i k} , D _k .

4.    Оценивание в зависимости от геометрического положения

Задавшись формулами (9) и (10), а также конкретным видом (6) матриц C ik (x * ) и D k (x * ), можно исследовать зависимость критериев J a и J a к от точки x * : J a = J a (x * ), J A к = J a к (x * ). Тем самым решается задача оценки точности в зависимости от взаимного геометрического положения области наблюдения и всех РЛС. Однако анализ зависимости затруднен вследствие того, что матрицы C ik (x * ), D k (x * ) зависят не только от x * , но и существенным образом от моментов времени измерений t i .

Первое слагаемое P - 1 (x * ) в формуле (10) имеет простое выражение, не зависящее от точки x _∗ и моментов измерений t i :

- 1

A A ^ ^

^σ ϕ²

n 1

... 2

σϕ m nm

Поскольку первое и второе слагаемые в (10) являются положительно определенными матрицами, матрица P - 1 (х * ) задает « фоновый » уровень точности для всех положений х * , который нельзя уменьшить.

Зависимость от геометрического положения x _∗ для задачи оценивания систематических ошибок по азимуту проявляется в формуле (10) через второе слагаемое. В важном частном случае, который исследуется ниже, удается избежать зависимости от моментов t i , и, как следствие, придать универсальный вид зависимости критериев J a (х * ) и J a к (х * ) от х * . Рассмотрим подробнее второе слагаемое.

Введем для каждой РЛС понятие среднего времени своих измерений (относительно времени t 0 ):

t k = — У (t i - t o ), I j = { i : 1 <  i <  n, k(i) = j } • ^{n k} i ∈ Ik

Также введем величины, которые можно назвать, соответственно, вторым и центрированным вторым моментами для времен измерений k-ой РЛС:

q k = - У (t i - t o ) ² ,   q k = - У (^ - t o - k k ) ² = q k

-

2 ^t k ^.

nn k i∈Ik                        k i∈Ik

Для удобства записи рассмотрим дополнительные матрицы

E k = [ e rk ⁽ x * ) e ^^{k (} x * ) ] , ^s k = [ 0     (r _k (x * )^) 2 ] •

Ниже не будем отмечать зависимость матриц и их компонентов от аргумента x _∗ . Отметим, что выполняются следующие соотношения:

— 1 TT           _nT ‘ pT     (nT ¹       ‘- 1 pT

E k = E k ,     D k ^ k D k = E k ^ k E k ,    ID k ^ k D k )    = E k ^ k E k •

Во введенных обозначениях блочные компоненты матрицы P ^-1 имеют вид

ϕ - 2 n 1 σ ₁

P a a =

ϕ n m σ m

P ee =

m

E Ek ^k—1 ET k=1

m

E tkEk ^k—1 ET k=1

m

E ^q k E k ^ k ^—1 E T k =1

m

E q k E k Ч^{- 1} E T k =1

P qa =

ϕ - 2

n 1 σ ₁    r ₁

t 1

e ϕ 1

e ϕ 1

n _m

^ϕ σ _m

m

Z4

t _m

[e 1 e ϕm

V 1 e ϕm

Для анализа выражений, получающихся при детальном рассмотрении этих блочных матриц, полезно определить «матрицу преобразования» S(t):

S (t) =

10 t 0 010t 0010 0001

которая будет в дальнейшем активно использоваться.

Вычислим элементы второго слагаемого в формуле (10):

m

= E

S (tk )

T

k=1

,^^-

,^^-

- 1

Q = P eA P AA

r i¹ S(* i )

T

r l

- 1

e ^ 1

,^^-

Z4

e ^ 1

t l e ^ 1

R = P ee

-

·

·

·

- 1

r _m

n k σ _k ^r

-1    T erkerk

O

O

·

·

·

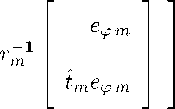
e ϕ m

T

S ( t m )

,

P eA P - l P Ae =

n k q k E k Е^ ¹ E T

m

S (t k ) = E

S ( t k )

T

A k

O

1^^-

k=1

O

q k B k

S (t k ).

С учетом новых обозначений формула (10) записывается следующим образом:

P AA = P '

+ Q ^T R ^-1 Q.

Видно, что матрица ковариаций P λ λ зависит от времен t i через параметры t k и q k .

Предложение 1. Пусть выполнено соотношение

Z4

t l =

Z4

.

.

.

— tm

^

= t.

Тогда в выражении матрицы P _{λ λ} отсутствуют времена измерений t i .

Доказательство. При условии (14) выражения (11)

и (12) приобретают вид

Q = S(tt) ^T r ^-1

R = S(t) ^T

m

E k=1

^e ^ 1

A k

O

O qkBk

- 1 r _m

e ϕm

= S(t) ^T Q,

S(t) = s(t) ^T R s (t).

Матрица S(t) обратима, и поэтому все матрицы S(t) взаимно уничтожаются в общем выражении Q ^T R ^-1 Q . Вследствие специфического вида матрицы Q в окончательное выражение от матрицы R входит только верхний левый блок, который равен 52m =1 A k и не содержит времен измерений t i . Компоненты Q также не содержат t i . Это завершает доказательство.

Матрицу P , посчитанную при условии (14), обозначим символом P ^∗ :

Paa = P - А1 + Q T R - 1 Q.

Условие (14) не требует наложения каких-либо сложных ограничений на процесс наблюдения, и (в приближенном смысле) выполняется естественным образом, например, если РЛС производят измерения с некоторым заданным шагом по времени.

Пример 1. Пусть k-я РЛС производит измерения на промежутке [0,^] в моменты tjk = t1k + ^k (jk 1) + ^jk , jk = 1, nk •

Здесь Ak — шаг наблюдения k-й РЛС, 6 j k — малая случайная погрешность: E { 6 j k } = 0, | 6 j k | ^ A k . В этих условиях выполнены соотношения

Zv t1

Z tm

ϑ

t 2 ^,

E { ^Z k } - |

< A.

- 2

5.    Анализ матрицы Р\х при приближенном выполнении (14)

В этой части рассмотрим подробнее ситуацию, приведенную в примере 1, а именно, случай приближенного выполнения соотношения (14). Интересен характер зависимости матрицы P _{λ λ} от малых вариаций величин t _k .

Заметим, что для матрицы S (t) справедливо следующее свойство:

S(t 1 + t 2 ) = S (t 1 )S (t 2 ) = S(t 2 )S(t 1 ) , V t i ,t 2 G R .

Предложение 2. Пусть выполнены соотношения tk = t + Ek , qk = (1 + ak) q,     Vk G 1,m,                    (16)

где ε k , α k — некоторые малые числа. Тогда

P xx = PG ⁺ E >j ⁺ o ( ^2 ) .               ⁽¹⁷⁾

Здесь H ij — матрицы, не зависящие от E k и t i ; ||e|² = Ekm=i e 2 — квадрат евклидовой нормы вектора-столбца, составленного из всех ε k .

Доказательство. Рассмотрим второе слагаемое в формуле (13) с учетом соотношений (11), (12). Каждую матрицу S(t k ) представим в виде произведения S(t k ) = S(E k )S(t) Получим следующие выражения:

Q = P ex P - X = S (tt) T   r -¹ S ( e i ) ^t

= S(t ) T

r

^e ϕ 1

ε 1 e ϕ 1

R = P ee - P 9A P -A 1 P A9 =

S (t) T

= S(tt) T

m

E Ak k=1

m

ε k A k k =1

^e ϕ 1

- 1

m

r _m ^-1 S ( E m ) ^T

e ϕ m

ε _m e ϕ _m

m

E S(Ek)T k=1

m 7

εkAk k=1

m

E ( qk Bk + Ek Ak k=1

e ϕ m

= S(t ) T Q _e ,

A k

O

O qkBk

S (E k ) S(tt) =

S(t) = S(t) T R _e S(t).

После этого формула (13) приобретает вид

P x A = P - A + Q T R - 1 Q _e

Обозначим через Г правый нижний блок 2 х 2 матрицы R _e 1 :

Г =

mm

< Е qkB» + Е£2 A^k - k=1        k=1

- 1

_{m        m}    - 1 _m

E » a »  E 4 E » a » b .

k=1      / \k=1   /     \k=1      /

Его можно представить в следующем виде:

r->+o ^) L

m           -1

^Г 0 = I E^{(1 + a} k )Bkj   •

Матрица Г о не зависит от величин E k и q. Все остальные блоки матрицы R _e ¹ выражаются через Г:

r ¹ =

_m - 1 _m - 1 _{m        m       m}   - 1      _m - 1 _m

( Й Ak) +( Й Ak) ( Й EkAk)Г( Й EkAk){ Й a5»)   —  Й a5»)   Й EkAk)Г k=1        k=1 k=1         k=1       k=1           k=1      k=1

-

m        m-1

^Г ^Й ^E k ^Akj ^Й ^Akj

Г

.

Окончательное выражение для P λ λ имеет вид

P AA = P AA

+ q T r - ¹ q _£ = p aA +

T r 1 e .1

.

.

.

T r m e _{ϕ m}

(E A ⁵ ») ¹ [ r* 1

••

•

r m e .m j ⁺

+

r 1 e T1

.

. .

T r _m e _{ϕ m}

-

-

_m - 1 _{m        m       m} - 1

E Aik   E Ek Aik Г E Ek Aik  E Aik k=1       k=1         k=1        k=1

~ T r 1 e. 1

.

.

.

T rmeϕ m

m - 1 m

Ib 7 lb E k A k^ Г l Е 1 Г 1 6 . 1 •••

^E1 r 1 e T 1

.

.

.

T ε _m r _m e _{ϕ m}

m       m- 1

^Г 1Ь ε k A k k=1 Ak\    r 1 e . 1

•

+

„т ^E1 r 1 e^ 1

.

.

.

ne_v 1

•

•

•

••

r m e ϕ m

-

ε m r m e ϕ m

-

r m e .m j ⁺

Г Еще . 1 •••

ε _m r _m e _{ϕ m}

.

T ε _m r _m e _{ϕ m}

Как видно, в этом выражении отсутствуют члены с ε k в степени 1. Члены с ε k в степени выше 2 появляются только при разложении Г по формуле (18). Также при этом разложении появляется множитель 1/q. Первые два слагаемых соответствуют P A а. □

Отметим, что формула (17) не только говорит об ≪ устойчивости ≫ матрицы P λλ к малым возмущениям в величинах t » , но и задает меру того, какие возмущения считать малыми. А именно: P aa в формуле (17) зависит от e » / ^ q. Т.е. малость E » определяется по сравнению с величиной ^ q — « характерным разбросом » времен t i .

6.    Численные построения

Соотношение (17) свидетельствует о том, что в практически важном случае (16) приближенного выполнения равенства (14) точность оценивания систематических ошибок РЛС по азимуту с хорошим качеством определяется формулой (15). Задавшись ею, можно численно построить зависимость критериев J λ , J λk от геометрического положения x _∗ центра области наблюдения на плоскости П. На рисунке представлены результаты численных расчетов функции ^ J a ( x *) для системы четырех РЛС Новосибирской зоны наблюдения. По осям откладывается расстояние в км. РЛС расположены в точках (0, 0), (1, - 2), (225, 33), (25, 380). Оттенки серого на графике соответствуют различным значениям критерия ^ J a ( x *) : более темные отвечают меньшим значениям.

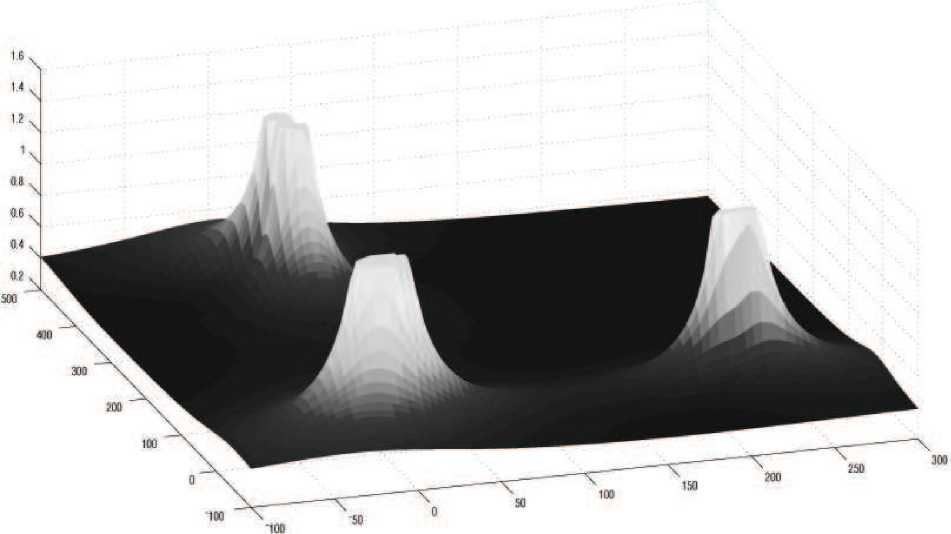
График критерия лУ J a ( x * )

Полученные в статье результаты могут быть применены в перспективных алгоритмах мультирадарной обработки.

При написании статьи использованы результаты работы автора по договору о сотрудничестве между Институтом математики и механики УрО РАН (г. Екатеринбург) и фирмой ≪ Новые информационные технологии в авиации ≫ (г. Санкт-Петербург). Работа поддержана УрО РАН (проект 12-П-1-1002) и РФФИ (проект 12-01-31247 мол_а).