Исследование устойчивости положения равновесия системы динамики биоценоза в условиях межвидового взаимодействия

Математическое моделирование динамики численности популяций является одной из основных проблем математической экологии. Ввиду многофакторности биотических и абиотических воздействий на биоценоз разработка модели представляет собой нетривиальную задачу.

Важнейшей характеристикой математических моделей, описывающих динамику численности биологических популяций, является наличие устойчивого или неустойчивого положения равновесия.

Одна из широко известных биологических моделей – модель динамики биоценоза в условиях межвидового взаимодействия, известная как модель «хищник-жертва»1:

dv

- = v i dt

i

^ M a T

dw

," = wk dt

к <

.j = 1

N

a ij w j

, i = 1, N , J

^- b k + У ъ_л , к         j = 1       J

k = 1, M , (1)

где Vj, i = 1, N - численность попу ляции i -ого вида жертв; w k ( t ) , k = 1, M - численность популяции k -ого вида хищников; a_i и b_k – разность между рождаемостью и смертностью i -ого вида жертв и k -ого вида хищников соответственно в предположении, что он не испытывает влияния внешних факторов; a_ij – коэффициент, характеризующий уменьшение i -ого вида жертв за счет j -ого вида хищников, a_ij > 0; b_kj – коэффициент, характеризующий увеличение k -ого вида хищников за счет j -ого вида жертв, b_k j >  0.

Учитывая, что численность популяции является неотрицательной величиной, рассмотрим с исте му (1) при усло вии, что v_; >  0 , i = 1, N , w_k > 0, k = 1, M .

Поскольку фазовые переменные данной системы отвечают численности различных видов популяций, вывод о динамике численности каждой из популяций можно сделать на основании исследования устойчивости положения равновесия системы по соответствующим переменным.

В статье рассматривается вопрос об устойчивости по части переменных нулевого положения равновесия системы (1) при условии, что рождаемость биологических видов не превышает

MORDOVIA UNIVERSITY BULLETIN смертности. Это условие может быть записано в виде:

a i <  0, i = i^ y ; b k >  0, k = 1Z M .

Зам етим, что в случа е, к огда a_i = 0 i = 1, N или b_k = 0, k = 1, M , матрица линейного приближения системы (1) имеет нулевые собственные значения, что соответствует критическому слу-чаю². В связи с этим вопрос об устойчивости нулевого положения равновесия по первому приближению остается открытым.

Для решения поставленной задачи применяется подход3–5 [1–2], основанный на установлении локальной асимптотической эквивалентности между решениями исследуемой системы и ее линейным приближением.

Обзор литературы

Основы математического подхода в экологии заложены в книге Т. Р. Маль-туса6. В этой работе впервые приведена постановка задачи о численности популяции в строгих математических формулировках, впоследствии получившая название модели Мальтуса; показано, что при отсутствии ограничивающих факторов численность может увеличиваться в геометрической прогрессии. Дальнейшее развитие математических моделей популяций было реализовано в работе П. Ф. Ферхюльста [3], где приведен анализ динамики численности популяции одного вида в условиях естественных ограничений – конкуренции за ресурсы. Исследование предложенных моделей было продолжено в трудах Р. Перла7 [4].

• ²    Малкин И. Г. Теория устойчивости движения . М. : Наука, 1966. 533 с.

• ³    Воскресенский Е. В. Методы сравнения в нелинейном анализе. Саратов : Изд-во Сарат. ун-та, 1990. 224 с.

• ⁴    Воскресенский Е. В. Асимптотические методы: теория и приложения . Саранск : СВМО, 2000. 300 с.

• ⁵    Шаманаев П. А., Язовцева О. С. Применение локальной покомпонентной асимптотической эквивалентности к исследованию устойчивости по части переменных решений динамических систем // Аналитические и численные методы моделирования естественно-научных и социальных проблем : мат-лы XII Междунар. науч.-техн. конф. Пенза : Пензенский государственный университет, 2017.

• ⁶    Malthus T. R. An essay of the principle of population . London : St. Paul’s Church-Yard, 1798. 126 p.

• ⁷    Pearl R. The biology of population growth. New York, 1930. 260 p.

Позднее был осуществлен переход от рассмотрения моделей, описывающих один вид, к системам, моделирующим динамику популяций в условиях межвидового взаимодействия8–9 [5]. Подобные модели получили название «хищник-жертва». Основой для составления систем послужили кинетические уравнения Лотки, описывающие гипотетическую химическую реакцию. Вольтерра предложил модификацию модели, учитывающую периодические колебания численности популяций при их взаимодействии.

Основные положения современного этапа развития математических моделей динамики численности популяций содержатся в различных ис-следованиях10–13 [1; 6].

Вопросы устойчивости математических моделей, описывающих динамику биологических популяций в условиях межвидового взаимодействия, изложены в многочисленных ра-ботах14–15 [7–11].

В книге Ю. А. Пыха на основе прямого метода Ляпунова развита общая теория исследования устойчивости равновесных режимов для широкого класса экологических и генетических моделей16.

Работа Ю. М. Свирижева и Д. О. Логофета посвящена исследованию устойчивости обобщенных моделей типа «хищник-жертва»17.

Том 28, № 3. 2018

Другими учеными проведен анализ положений равновесия модели Лотки-Вольтерра на примере динамики популяций рыб, получен критерий бифуркации Хопфа для данной модели [7].

К исследованию математической модели для трех видов индийскими и арабскими учеными применены теория устойчивости и теория бифуркаций. Получены условия, при которых система теряет устойчивость и в ней возникают колебания предельного цикла [8].

Исследователи З. Ма, С. Вонг и др. описывают математическую модель динамики биоценоза с функциональным откликом. В работе приведены результаты анализа поведения решений системы, показано влияние функционального отклика на динамику системы [9].

Итальянскими учеными проанализировано поведение решений модели Лотки-Вольтерра на длительном промежутке времени. Получены условия устойчивости для положений равновесия, имеющих биологический смысл [10].

В статье китайского исследователя рассмотрена модель «хищник-жертва» с функциональным откликом, для которой определены условия существования единственного положительного решения, исследованы его локальная и глобальная асимптотическая устойчивость [11].

В работах других авторов содержится обзор исследований в области устойчивости по части переменных решений дифференциальных уравнений, приведены многочисленные приложения, в т. ч. из популяционной динами-ки18–19.

П. Руш, П. Абетс и М. Лалуа на основании прямого метода Ляпунова исследуют устойчивость по части переменных положений равновесия математической модели динамики би- оценоза в условиях межвидового взаимодействия для трех видов, два из которых питаются третьим20.

Другими учеными изложены задачи об устойчивости по части переменных крупномасштабных (сложных) систем дифференциальных уравнений и экологических систем Лотки-Вольтерры [12–13].

Материалы и методы

В работах авторов получены достаточные условия устойчивости по части переменных нулевого положения равновесия нелинейных систем обыкновенных дифференциальных уравнений с возмущениями в виде векторных полиномов на основе локальной покомпонентной асимптотической эквива-лентности21 [2]. Система (1) относится к указанному классу систем и может быть представлена в виде:

— = Ax + P ( x ) , dt ⁽ )

где x е Rⁿ ; x = colon(v,w ); v = colon ( v 1 ,..., v ^ ); w = colon ( w ₁,..., w_M ); A – диагональная ( n x n )-матрица вида

A = diag ( a_v..., aN, - b_v..., - Ьм ) ,

P ( x ) = colon ( P 1 ( x ),..., P_n ( x ) ) ,

M

Pt (x )=-Eajviwj, i=1,N, j=1

N

P N + k ( ^x ) = ^bwvj , ^k = 1, M .

j = 1

Вместе с тем для систем вида (2) условия устойчивости нулевого положения равновесия могут быть ослаблены.

Сформулируем достаточные условия локальной асимптотической эквивалентности системы (2) и ее линейного приближения dy

— = Ay dt

и на основании этих условий исследуем вопрос об устойчивости по части переменных нулевого положения равновесия системы (2).

Теорема

Пусть выполняются условия ai < 0 (i = 1, N), bk > 0 (k = 1, M) (4)

или ai = 0 (i = 1, N), bk > 0 (k = 1, M). (5)

Тогда системы (2) и (3) являются локально асимптотически эквивалентными по Брауеру, а нулевое решение системы (2) обладает следующими свойствами:

• 1)    в случае выполнения (4) асимптоти чес ки устойчиво по компонентам v_f , i = 1, N , асимптотически устойчиво

по тем компонентам w_k , для которых b_k > 0; устойчиво по тем компонентам w_k , для которых b_k = 0, причем по этим компонентам w_k система имеет локаль ное асимптотическое равновесие, k = 1, M ;

• 2)    в случае выполнения (5) устойчиво по компонентам v _t , i = 1, N и асимптотиче ски устойчиво по компонентам w_k, k = 1, M , причем по компонентам v , система имеет локальное асимптотическое равновесие.

Доказательство

Построим банахово пространство

Q = { x : x е C ( [ T , +« ) , R n ) ,

I v, (t )|< cePi, p (t )|< cepN+kt, t > 0, c е R +,i = IN, k = \M} с нормой

||x||n = max sup {vf (t)|ce"Pit, |wk (t)ce"Pn+kt}, “ i=1, N k=1M где при справедливости условия (4) полагаем

P n + k =

I ^- b k , b k > ⁰

, k = 1, M ;

а при справедливости условия (5) ‒

Здесь e - достаточно малое положительное число, которое выбирается таким образом, что a i + 8 <  0 при условии (4) и - b_{N +} k + 8 <  0 при условии (5).

В банаховом пространстве О рассмотрим операторное уравнение x= Lx,             (6)

где L = colon (( Lx ) 1 , ..., ( Lx ) _n ), причем при выполнении условия (4) компоненты оператора L имеют вид:

(Lx), = е-'у™-

^4 t-■)v, (s) »,(s) ds, I = 1JV, j=1    0

( Lx ) n ₊ k = e" ^bkt y N + k ^-

-^ f e" b k ⁽ t - ' ) w_k ( " ) V j ( " ) ds , ^k = 1M .

j=1      t а при выполнении условия (5) – j=1 t

( Lx ) N + k = e b - tyak +

+& j e" b ' ‘ t ^- ' ⁾ w - ( ¹ ) V j ( ¹ ) ds , - = i^M .

j = 1    0

Из построения оператора L следует, что решение x ( t ) операторного уравнения (6) является также решением системы (2), причем начальные данные решений систем (2) и (3) при условии (4) связаны соотношениями

х(0) = _у(0), i = 1, N, xisk=^;; k-::*.//was) vj( s) ds, j=10

k = 1PM,(7)

а при выполнении (5) – x!«>= л<0’+]^Л,р, (s) w, (s) ds, i = 1,N, j=10

^№' k = yN0)k, k = 1, M.(8)

Покажем, что L : Q ₀ ^ Q ₀, где

Q0 = {x: I|x||fi < c0, c0 e R+ } для некото- рого достаточного малого с0.

Пусть x _Ω ≤ c ₀ . Тогда для компонент оператора L в случае выполнения условия (4) справедливы оценки

Если выполняется (5), то выберем с0 такое, что верны следующие оценки:

M

I (Lx )/l

, ( a, + e ) t <  e ⁽ i ’

M

| Z^ c 2 У a j d j j = 1

i = I, N ;

a

0 = c „ max <  У — > <  1,

^{1    0} i = 1, N ^ A ’

j = 1

b j

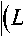
x ) N +J

. - b k t

N     ( a j ^{+ £} ) t

| yl k\ + С У 4— -л j = i - ( a j + £ )

C 0 = — max ^ £ ^k = 1,^M

N

iax УЬ< > <  1. kj .

M ■■ J

k = 1, M ,              (9)

I j = 1

Выберем _ y ^{( 0 )} и ^ 5 ° + _k такие, что

где

dj

В случае выполнения условия (5) получим:

M — b j t

I (Lx), I ^ I y0) I+c2 У 4- ay, i=1,N ’ j=i by

I ( Lx ) . +J ^ e ⁽ - b k ^{+ 6} )

2 N y N i . + ^ct X b kj ⁶ j = 1

|.v ! ⁰⁾| s ( 1 - 61 ) c 0 , i = 1, N ,

|.y ( 0 + k |< ( 1 - Л ) c o , k = VM . (13)

Тогда при выполнении условия (4) из оценок (9) и (13) следует:

I ( Lx ) ,|

< c о e ^{( a} - ^{+ 6} ) t , i = 1, N ;

I⁽ Lx ) ^ +J - ^c о e ⁵ " ⁺ k t , ^k = 1’ ^M ■

Если выполняется условие (5), то из оценок (9) и (13) получим:

| ( Lx ) i | <  c o , i = 1, N ;

k = 1, M .           (10)

I(Lx) n+J

-₀ e ^{( - bk + 6} ) t , k = 1, M .

В случае выполнения (4) выберем с ₀ такое, что справедливы следующие оценки:

0 = c_n max <  ^{1 0} , = 1; ^

-iy^d_J\< 1;

„ j = 1

N

0 = c _n max < У

2   0 ^k = ^M j

b j

k 1. (11)

Следовательно, Lx _Ω ≤ c ₀ при всех x ∈ Ω ₀ .

Аналогично работе Е. В. Воскре-сенского²² доказывается, что оператор L является вполне непрерывным на Ω₀ и, следовательно, удовлетворяет всем условиям принципа Шаудера²³ о существовании неподвижной точки для уравнения (6).

Учитывая оценки (9) и (12), в случае справедливости условия (4) и b_k = 0 при всех t ≥ 0 , получим

|x_t ( t : 0, x ^{( 0 )}

—

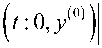
< 01 c 0 e(ai+6) t, i = 1, N;

(0)                               (0)

I x N + k ( t • ⁰, x ) y N + k ( t • ⁰, y ) <

< 02 c0 e(a0+E) t, k = 1, M, где a= max a; при bk > 0 при всех 0     i=1,N i t ≥ 0 имеем

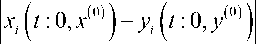
< 91 c о eai, г = 1, N;

|xN + k ( t : 0, x ^{( 0 )}) - y N + k ( t : 0, y ^{( 0 )} )| <

• <    0 2 c ₀ e - b k t , k = 1^M .

Если же выполняются условия (5), то при всех t ≥ 0

^ ■( t :0, x ^{( 0 )}) - X -( t :0, У ^{( 0 )}) ^

• <    0 1 c о e ^- b ⁰ t ,i' = 1Л;

(0)                               (0)

|xN + k ( t • ⁰, x ) y N + k ( t • ⁰, y ) —

• <    0 2 c ₀ e ( - b k ^{+ E} ) t , k = A^M .

где b ₀ = m in b_k .

k = 1, M

Поскольку a i + e < 0, i = 1, N , - b_k + e < 0, k = 1, M , то

I x ( t : 0, x ^{( 0 )}) - y ( t :0, y ^{( 0 )} )|| ^ 0 при t ^ +m , равномерно по x ⁽⁰⁾ и y ⁽⁰⁾.

Поскольку системы (2) и (3) являются локально асимптотически эквивалентными по Брауеру и выполняются условия теоремы 1.1 из работы [6], то свойство устойчивости и асимптотической устойчивости компонент решений системы (2) полностью определяются поведением соответствующих компонент решений системы (3). Отсюда следует, что нулевое решение системы (2) обладает свойствами 1‒2, приведенными в формулировке теоремы.

Доказательство завершено

Результаты исследования

В качестве примера рассмотрим модель вида (1) в случае, когда два вида питаются третьим [7]:

dv

— = alV1 - allV1 wi - ai2V1 w2, dt dw

• -    = - b i w i + b n w i v i , dt

dw

• -    = b 2 w 2 + b 2i w 2 v i , dt

  
  

где a ₁, b ₁, b ₂ удовлетворяют условиям (4) и (5); a ₁₁, a ₁₂, b ₁₁, b ₂₁ – положительны.

В этом случае у системы (14) существует только нулевое положение равновесия. Исследуем его на устойчивость по части переменных.

Из выполнения условий теоремы можно сделать следующие выводы об устойчивости по части переменных нулевого положения равновесия нелинейной системы (14):

• 1)    при a ₁< 0, b ₁ > 0, b ₂ = 0 асимптотически устойчиво по переменным v ₁, w ₁ и устойчиво по переменной w₂ , причем по переменной w₂ имеется локальное асимптотическое равновесие;

• 2)    при a ₁< 0, b ₁ = 0, b ₂ > 0 асимптотически устойчиво по переменным v ₁, w ₂ и устойчиво по переменной w ₁, причем по переменной w ₁ имеется локальное асимптотическое равновесие;

• 3)    при a ₁< 0, b ₁ = 0, b ₂ = 0 асимптотически устойчиво по переменной v ₁ и устойчиво по переменным w ₁, w ₂, причем по переменным w ₁ и w ₂ имеется локальное асимптотическое равновесие;

• 4)    при a ₁ = 0, b ₁ > 0, b ₂ > 0 устойчиво по переменной v ₁ и асимптотически устойчиво по переменным w ₁, w ₂, причем по переменной v ₁ имеется локальное асимптотическое равновесие.

Для проведения численного моделирования выбраны три группы коэффициентов рождаемости и смертности a1, b1, b2 (см. рис. 1–3), соответствующие условиям 2)–4). Графики решений для случая 1) соответствуют случаю 2), если переменные w1 и w2 в системе (14) поменять местами. В качестве значений параметров aij, bij были выбраны следующие: a11 = 0,03; a12 = 0,02; b11 = 0,2; b21 = 0,1. Начальные значения численностей популяций «жертв» и «хищников» определены следующим образом: V1(0) = 4, ^1(0) = 5, w2(0) = 7.

Приведем графики, отражающие динамику численности популяций в исследуемой модели.

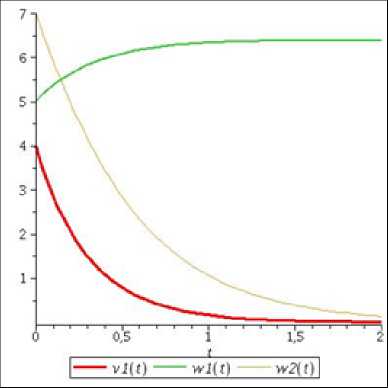
Р и с. 1. Графики компонент решений системы (14) при а 1 = — 3, Ь 1 = 0, b 2 = 2

F i g. 1. Graphs of solution components of system (14) at a 1 = — 3, b 1 = 0, b 2 = 2

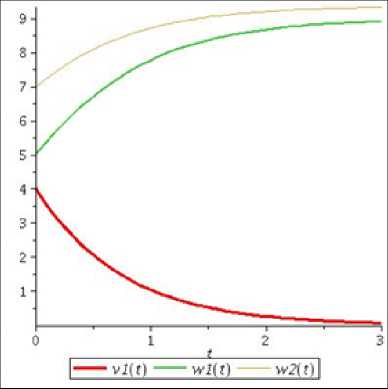
Р и с. 2. Графики компонент решений системы (14) при а 1 = - 1, Ь 1 = 0, b 2 = 0

F i g. 2. Graphs of solution components of system (14) at a 1 = - 1, b 1 = 0, b 2 = 0

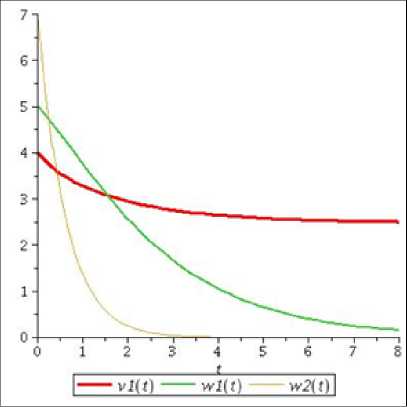
Р и с. 3. Графики компонент решений системы (14) при a ₁ = 0, b ₁ = 1, b ₂ = 2

F i g. 3. Graphs of solution components of system (14) at a ₁ = 0, b ₁ = 1, b ₂ = 2

Обсуждение и заключения

Как видно из рис. 1, численности популяций второго вида «хищников» и «жертв» убывают, а численность первого вида «хищников» увеличивается до определенного предела, что подтверждается полученными аналитическими результатами. Таким образом, если рождаемость и смертность одного вида «хищников» равны, а у второго вида «хищников» и «жертв» смертность превышает рождаемость, то независимо от значений остальных параметров произойдет стабилизация численности первой популяции и вымирание двух других.

На рис. 2 численность «жертв» стремится к нулевому значению, а численность популяций «хищников» с те- чением времени приходит к постоянному значению. Действительно, если коэффициент смертности больше коэффициента рождаемости для «жертв», но при этом рождаемость и смертность «хищников» равны, то происходит вымирание «жертв» и стабилизация численности «хищников».

Из рис. 3 следует, что если смертность двух популяций, истребляющих третью, превышает рождаемость, а рождаемость и смертность третьей популяции равны, то независимо от значений остальных параметров, численность популяции «жертв» и первой популяции «хищников» с течением времени убывают, а численность другой популяции «хищников» стабилизируется.

Все авторы прочитали и одобрили окончательный вариант рукописи.

о ВЕСТНИК МОРДОВСКОГО УНИВЕРСИТЕТА Том 28, № 3. 2018 arts/lokalnaya-pokomponentnaya-asimptoticheskaya-ekvivalentnost-i-ee-primenenie-k-issledovaniyu- ustojchivosti-po-chasti-peremennyx (In Russ.)