Исследование вероятностного распределения типа гиперболического косинуса

Вероятностным распределением типа гиперболического косинуса называют трехпараметрическое распределение с характеристической функцией

Гоо f (t) = I ch—t - i—sh—t I , где —, в, m e R, m > 0, в Ф 0.(1)

( m в m )

Впервые функция (1) получена автором при решении задачи характеризации распределений свойством постоянства регрессии квадратичной статистики Q на линейную статистику Л [1]:

nnn

E(Q\Л) = E(Q), где Q = VVUjkXjXk; Л = £Xj .(2)

j=1 k=1

X 1 , X ₂,..., X n - независимые, одинаково распределенные случайные величины. В зависимости от соотношения коэффициентов статистики Q условие постоянства регрессии (2) является характе-ризационным (характеристическим) для ряда известных распределений [2 - 4] и, в частности, распределения типа гиперболического косинуса.

Указанное трехпараметрическое распределение является обобщением двухпараметрического распределения Майкснера (J. Meixner) [5, 6] с характеристической функцией f (t) = ( ch t - i9 sh t) m, m > 0, 9e R.

Распределение Майкснера получается, если в (1) положить в = m и переобозначить параметр —в = — m = 9 . Наличие третьего параметра позволяет получить большее разнообразие распределений: каждое двухпараметрическое распределение Майкснера с конкретными параметрами ( 9 , m ) является семейством распределений с параметром в • Например, при 9 = 2, m = 1 получаем тройку параметров ( — = 2 в , m = 1, в ), где в ^е R, в Ф 0. В частности, эти параметры ( — , m , в ) могут быть (2; 1; 1) - распределение Майкснера, а также (1; 1; 0,5), (-1; 1; -0,5), (4; 1; 2) и т. д. Заметим, что в трехпараметрическом распределении математическое ожидание случайной величины равно параметру — . При этом параметр — является параметром не только сдвига, но и участвует в формировании дисперсии и других моментов.

В частности, при — = 0, m = 1 из (1) получаем характеристическую функцию однопараметрического распределения гиперболического косинуса (секанса). При сдвиге случайной величины, распределенной по закону гиперболического косинуса, на величину X получим двухпараметрическое распределение, известное как распределение Чампернауна [7].

Таким образом, распределение типа гиперболического косинуса оказывается обобщением двухпараметрического распределения Майкснера, которое, в свою очередь, является обобщением однопараметрического распределения гиперболического косинуса на случай µ ≠ 0 .

В данной работе восполняются пробелы в доказательной части теории: представлено обоснование найденного ранее распределения и выведен ряд соотношений.

Исследование характеристической функции

Докажем, что функция f ( t ) вида (1), полученная как результат характеризации распределений свойством постоянства регрессии, действительно является характеристической функцией.

Теорема 1. Функция

^{q ( t )} ch ^β t - i ^µ sh ^β t ^{,                                     (3)}

m βm где µ , β, m – действительные постоянные, β, m ≠ 0 , является характеристической функцией не- которого распределения.

Доказательство теоремы 1. Для доказательства теоремы потребуются две леммы.

Лемма 1. Функция q ( t ) = ch ^β t - i ^µ sh ^β t ,                                      (4)

m βm где µ , β, m – действительные константы, β, m ≠ 0 , является целой функцией порядка 1.

Доказательство леммы 1. Для доказательства леммы 1 достаточно проверить условия Коши–Римана применительно к функции комплексной переменной q(z) вида (4), которые справед- ливы на всей комплексной плоскости. Порядок целой функции q(z) определяют функции ch βz m

β и sh z , которые являются целыми функциями первого порядка. m

Лемма 2. Задана функция

β µβ

q(z) =ch z - i sh z , m   βm где µ, β, m – действительные константы, β, m ≠ 0 . Тогда а) q(z) имеет лишь чисто мнимые ну ли; б) все нули функции q(z) простые; в) z = 0 не является нулем функции q(z) .

Доказательство леммы 2. Положим, q(z) = 0 . Решая указанное уравнение с использованием формулы cth z = i ctg iz , получаем ctg i βz = µ. Отсюда находим нули функции q(z) :

mβ

im l Д I

z = - arcctg   + π k   k ∈ Z .

k в I g в J

Из (5) следует справедливость утверждений а) и б) леммы 2. Утверждение в) проверяется непосредственно. Лемма 2 доказана.

Переходим к доказательству теоремы 1. Для целой функции q ( z ) вида (4) применим теорему Вейерштрасса о факторизации целых функций [8]:

+∞

q ( z ) = z ^{S 0} e ^{η ( z )} ∏ k =-∞

7 [е

-

X      1 mkI ezz zk J     .

.

Упростим данное выражение, используя утверждения леммы 1: так как z = 0 не является нулем функции q ( z ) , то S ₀ = 0 ; так как все корни z_k простые, то все m_k равны 1, k ∈ Z .

Следовательно,

+∞

q(z) = e * z ⁾ П 1 -“I e zz .

k =—^ \ z k J

Математика

Исходя из (5), обозначим zk =——, * e Z, где 8k - действительные и различные при раз-k     Bk                  k ных k . Тогда

+^

q ( z ) = e ^{n ( z} ) П ( 1 — i8 * z ) e^

.

к =—^

Поскольку, согласно лемме 1, q ( z ) - целая функция первого порядка, то п (z ) - многочлен степени не выше первой, а именно: n ( z ) = az + b . Из условия q (0) = 1 и из (6) следует, что b = 0.

Таким образом, (6) принимает вид

+^

q ⁽ z ) = e ^az П ( 1 ^{— i8} * ^z ) e i⁸ * ² .

* =—^

Перейдем к действительной переменной t , тогда

+^ q ( * ) = e a* П ( 1 — i8 * * ) e i⁸ * * .

* =—^

Для определения a продифференцируем функцию q ( t ) , заданную соотношением (7):

q ‘ ( * ) = ae a*

(

П ( 1 — i⁸ * * ) e *

V * =—~

+ e a* 7

f +^

ПО - iB k t )       .

V * =—~

Из (8) следует q‘(0) = a + i8, где 8 - действительное число. Однако, из (4) получаем qz(0) = -i —. Два последних соотношения приводят к выводу, что a - чисто мнимое (возможно, m a = 0). Положим, a = iA, где A - действительная постоянная.

Подставив это значение в (7), приходим к выражению

+^

q ( * ) = e iA* П ( 1 — iB * * ) e к =—^

Тогда

+^ 7

— = e ^{— iA}* П q ⁽ * )         * 1—L

\

1 — iB * , k

e — i8_**

Функции-сомножители в правой части (9) являются характеристическими функциями:

e ^— i^A* , e ^—'

1 — i8 * *

^iBkt – характеристические функции вырожденного распределения,

- характеристическая функция гамма-распределения при 8* > 0 и характеристиче ская функция распределения, сопряженного с гамма-распределением при 8* < 0.

Введем функцию h_n ( t ) следующим образом

n hn (*) = e-iA* П

( 1

\

* =— n V

¹ - i⁸ * * ,

e ^— i⁸ * *

.

Согласно известному свойству произведения характеристических функций, функция h_n ( t ) при любом конечном n является характеристической. Из (9), (10) следует, что

4т = lim hn ⁽ * ). q ( * ) n ^^

По следствию из теоремы непрерывности характеристических функций ([9], следствие 2 тео ремы 3.6.1) предельная функция также является характеристической функцией. Таким об-q(t)

разом, теорема 1 доказана. Отметим, что соотношения (10), (11) представляют структуру характеристических функций вида (3).

Исследуем найденное распределение на безграничную делимость.

Теорема 2. Функция

1 ___________1__________

q(t) ch^t - i— sh^t m в m является безгранично делимой характеристической функцией.

Доказательство теоремы 2. Согласно теореме 1, функция является характеристиче- q ( t )

ской функцией. Обратимся к доказательству теоремы 1.

Из (10) следует, что характеристическая функция h_n ( t ) является произведением конечного числа безгранично делимых характеристических функций гамма-распределения и вырожденного распределения. Следовательно ([9], теорема 5.3.2), h_n ( t ) также безгранично делима.

Характеристическая функция безгранично делима, поскольку, согласно (11), является q ( t )

пределом последовательности безгранично делимых характеристических функций h_n ( t ) ([9], теорема 5.3.3).

Теорема 2 доказана.

f о          о \ - ^m

Теорема 3. Функция f (t) _ I ch — t - i — sh — t I при любом m > 0 является безгранично

l m   в m )

делимой характеристической функцией.

Доказательство теоремы 3. Поскольку любая положительная степень безгранично делимой характеристической функции сама является характеристической функцией ([9], следствие f 1 ^ m v q (t) J

, m > 0

теоремы 5.3.3), а функция —— безгранично делима, согласно теореме 2, то f ( t ) _ q ( t )

также является характеристической функцией, причем безгранично делимой. Теорема 3 доказана.

Вывод соотношений для плотности распределения вероятностей

Плотность распределения p_m ( x ) как обратное преобразование Фурье характеристической функции f ( t ) вида (1) при в >  0 имеет вид [10]:

+^                +^

P m ⁽ x ) ^_^ J e" itx f ⁽ t ) ^{dt _}^ J

2 п ^J              2 п ^J

-^

-^

e - itx dt

(ch P t - i ^— sh P t ) m

_ 2m-2 mem-1 f в - i— ) imxP B f m - limx.m + imx ^ =    7    7m l в + i—J I 2 2в ’2 + 2в J,

п ^{( в} 2 ⁺ — ^{2 ) 2}

где i _ V-1, B ( p ; q ) - бета-функция, а сомножитель с мнимой единицей имеет вид:

i

A . I ^-i— I l в + i— )

t 2 в— arctg e    в2 -—2

.  2Р— arctg - . +п sign— e в2 -—2

п ■

~ sign— e2

при

при

при

в - —2 > о,

в - —2 < о,

в ² - — ² = о.

При целых m функцию плотности в (12) можно выразить в элементарных функциях .

Теорема 4. При m _ 1 функция плотности p_m ( x ) имеет вид:

Математика

x

A 2 —

P 1 ⁽ x ) = /

2 J в ² + — 2 ch

2—

Справедливость (14) следует из (12) при использовании известных соотношений:

B

z ;

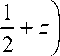
П

-------, cos iz = ch z . cos n z

Теорема 5. При m = 2 функция плотности p_m ( x ) имеет вид:

x

P 2 ^{( x} ) =

2 xA ^—

( в ² + — 2 )sh —

Справедливость (15) следует из (12) при использовании известных соотношений nz

B ( 1 + z ;1 - z ) =------- , sin iz = i sh z .

sin n z

Также отметим, что при целых m случайная величина X с характеристической функцией вида (1) представляет собой сумму m независимых случайных величин X1 + X2 +... + Xm , каждая из которых обладает характеристической функцией f (t) = | ch—t — i—sh—t V m — m

Следовательно, функция p ₂( x ) вида (15) как плотность вероятностей распределения суммы независимых одинаково распределенных случайных величин X ₁ , X ₂ является сверткой:

^

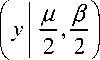
P 2 ( x ) = J P 1 ( y ) P 1 ( x — y ) dy , где p ( y ) = p

—^

Теорема 6. При m = 3,5,7,... функция плотности p_m ( x ) имеет вид:

mx     m — 1

P m ^{( x} ) =------- m m A ^ П [ ⁽² n ^{— 1) 2 —} 2 ⁺ m ^{2 x 2 ]} .

n mx

2( — ² + — ² ) ² ( m — 1)! chi — n =

Доказательство теоремы 6. Итак, полагаем m = 2 k + 1 ( k = 1,2,...). Тогда

I m-	imx	m	imx
B I 2	2 —	;T +	2 —
r.	1	imx ।	I
Г k +			1 г
V	2	2 ^ V	V

„ I , 1 imx , 1 imx = B k +--- ; k + - +---

(    2 2 —    2 2 —

—

, I 1 imx k + - +--

1 2 2 —

Г( k + z) Г( k + z)

Г (2 k + 1)                        (2 k )!

1 imx где Г(...) - гамма-функция, z = 2 — -2—, z и z

— комплексно-сопряженные величины.

По свойствам гамма-функции

Г ( k + z ) = ( k — 1 + z )( k — 2 + z ) ... z Г ( z ), ГI-- to\ ГI- + to\ =-------

V 2 J ^ 2    ) cos nto

получаем

Г ( k + z ) Г ( k + z ) =

1 imx 11 3 imx

2 2— J( 2 2—

2 k — 1 imx

2    2 —

x

1 imx

--1--

2 2 в

= ¹ +

3 imx |

— । -- .

2 2 P J

2 2V m x

к 4 4 в

'² J

..

- +

2 k - 1

к 2

m ² x ²

к 4 4 в

’2 J

.

.

imx

+--

2 P

.

( 1 imx I f 1 imx

11 I к 2 2рJ к 2 2р

f <2 k ^¹> i +

к

2 2 Л m x

4 P ,

п inmx cos

.

2 в

В последнем выражении перейдем к функции гиперболического косинуса, cos i to = ch to , за- m - 1

меним значение k на 2 и вынесем общие множители слагаемых в скобках. Тогда

B

m imx m imx I = П ( р + m ² x ² )(9 P 2 + m ² x ² )...(( m - 2) ² р + m ² x ² ) 7 ^- 2 P ’7 ⁺ 2 P J "            2 m - 1 _p m - 1₍ m _ _1)!ch n mx

2 P

2 m - i e m ^{- 1} ( m - i)!ch

.

Следовательно, исходя из выражения (12) и соотношений (13), (17), для функции плотности вероятностей при m = 3,5, 7,... приходим к формуле (16). Теорема 6 доказана.

Теорема 7. При m = 4,6,8,... функция плотности p_m ( x ) имеет вид:

P m ( X ) =

m 2 x

m

2( P 2 + Ц ² ) ² ( m - 1)!

Доказательство теоремы 7. Полагаем m = 2 k

mx

A 2 ^е

. nmx sh

m 1

П ( 4 n ² в 2 + m ² x ² ) .

n = 1

2 P

( k = 2,4,...). Тогда

„ (m   imx m   imx )   „ f,    ikx , ikx

B\; += B k;k + к 2  2в 2  2вJ к   P P

_\ , ikx i^i , ikx ।

Г kГ k +x         x к р J к P J = Г( k - z )Г( k + z)

ikx     m

,где ^z = Т, ^k = у. ^{р     2}

Г (2 k )

(2 k - 1)!

Вновь используем свойства гамма-функции:

Г ( k + z ) = ( k - 1 + z )( k - 2 + z ) ... (1 + z ) Г (1 + z ), Г ( k - z ) = ( k - 1 - z )( k - 2 - z ) ... (1 - z ) Г (1 - z ),

Г(1 - z )Г(1 + z ) = -^z- sin nz и получаем

Г ( k - z ) Г ( k + z ) = ( ( k - 1 ) 2 - z ² )( ( k - 2 ) 2 - z ² ) ... ( 1 ² - z ² ) 1 ( 1 - z ) Г ( 1 + z ) =

( 1 - z ² )( 4 - z ² ) ... ( ( k - 1) ² - z ² )^ z \         / \          )    \                   / oi_n 77

^{1 +} к

k ² x ² ^k. k ² x ²

"^2" 4 +

P Jк ^р J

( k - 1) ² + к

k ² x ² I

ikx п—

P

R ²      . ikx

^{P J} sin п— P

В последнем выражении перейдем к функции гиперболического синуса, sinito = ishto, и вы- несем общие множители слагаемых в скобках. Тогда m imx m imxI (P2 + k2x2)(4P2 + k2x2)...((k-1)2P2 + k2x2)nkx

---; —+--=-----------------------------;---------------

• ^{2 2 P 2 2 P J}             P k ^{- 1}(2 k -»«. ^пв

Таким образом, согласно соотношениям (13), (19), для функции плотности вероятностей, заданной (12), при m = 4,6,8,... приходим к формуле (18). Теорема 7 доказана.

Можно доказать, что в общем случае

2 P ² + Ц      2 Ц

E ( X ) = ц ; о =    ^; / 1 = ^^;

m       m o

Y 2 =- ⁺ m

Г

к

2 ц I ² m o J

Математика

где σ ² = V ( X ) , γ ₁ = As ( X ), γ ₂ = Ex ( X ) . Исходя из указанных соотношений, легко найти зависимость параметров µ , β , m от первых моментов:

µ = E ( X );    m = 2 ^µ = 2 ; β ² = m σ ² - µ ² .

γ 1 σ γ 2 - γ 1²

В статистическом анализе данных найденные соотношения позволяют использовать метод моментов. При обработке реальных данных из области медицины и здравоохранения (различные показатели физического состояния и показатели заболеваемости населения) с помощью разработанного программного обеспечения установлено согласие многих из них с распределением типа гиперболического косинуса [11].

Заключение

Можно найти примеры применения указанного распределения кроме вероятностных. В частности, в [12, 13] представлено множество нетривиальных интегралов, вычисляемых на основе моментов распределения при различных параметрах. В [14] также из найденных взаимосвязи и структуры моментов распределения типа гиперболического косинуса сформировано структурированное множество в виде бесконечной числовой призмы, исследован ряд её сечений, в частности, в связи с числами Стирлинга первого рода и коэффициентами полиномов Бесселя. В [15] в качестве сечений числовой призмы представлены и систематизированы как широко известные классические, так и числовые треугольники, и числовые последовательности, ранее в литературе не встречавшиеся. Для них найдены многие интересные свойства и соотношения.

Работа выполнена при финансовой поддержке проектной части государственного задания в сфере научной активности Министерства образования и науки Российской Федерации, проект № 1.949.2014/K.