Исследование вязкоупругих круговых цилиндрических панелей переменной толщины
Автор: Абдикаримов Рустамхан Алимханович, Худаяров Бахтияр Алимович
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 1 т.5, 2012 года.
Бесплатный доступ
В работе рассматривается задача исследования колебаний вязкоупругих цилиндрических панелей переменной толщины. Колебания относительно прогибов описываются системой интегро-дифференциальных уравнений (ИДУ) в частных производных. При помощи метода Бубнова-Галеркина, основанного на многочленной аппроксимации прогибов, задача сводится к системе обыкновенных ИДУ, где независимой переменной является время. Решения ИДУ определяются численным методом, базирующемся на исключении особенности в ядре релаксации интегрального оператора. Представляется алгоритм численного решения, созданный на основе этого метода. При исследовании нелинейных колебаний вязкоупругих цилиндрических панелей переменной толщины выявлен ряд новых механических эффектов.
Цилиндрическая панель, переменная толщина, вязкоупругость, нелинейные колебания, интегро-дифференциальные уравнения, численный метод
Короткий адрес: https://sciup.org/14320589
IDR: 14320589 | УДК: 539.3
Текст научной статьи Исследование вязкоупругих круговых цилиндрических панелей переменной толщины
В современной технике широкое распространение получили тонкостенные элементы конструкций типа пластин, панелей и оболочек переменной толщины. Такие элементы часто подвергаются значительным силовым нагрузкам, как статическим, так и динамическим. Обеспечение прочности, жесткости, надежности и высокой экономичности таких элементов имеет большое значение. Следует отметить, что в тех местах элементов, где необходима дополнительная жесткость или прочность, часто прибегают к наиболее простому способу — увеличению толщины оболочки.
В литературе имеется ряд работ, посвященных исследованию этой проблемы [1–7]. Здесь закон изменения толщины пластин и оболочек берется в виде линейной, квадратичной и других функций и рассматриваются различные вопросы поведения тонкостенных элементов конструкций при действии статических и динамических нагрузок.
Быстрый темп технического прогресса обусловливает необходимость решения всё более сложных задач. К усложнению приводит использование в инженерных конструкциях материалов с заданным комплексом физико-механических свойств. К числу таких материалов относятся композиционные материалы. Поэтому проектирование и последующее создание легких, но вместе с тем прочных и надежных конструкций требует дальнейшего совершенствования механических моделей деформируемых тел, а также разработки новых интегральных методов их расчета с учетом реальных свойств конструкционных материалов (например, вязкоупругости).
Кроме того, изготовление пластин, панелей и оболочек с плавным изменением толщины до недавнего времени было связано с реальными технологическими трудностями. В настоящее время достигнуты успехи в технологиях изготовления тонкостенных элементов конструкций любой формы по заранее заданным законам изменения толщины. В таком случае всю конструкцию следует рассматривать как конструкцию переменной толщины.
Расчет пластин и оболочек переменной толщины ставит перед исследователями сложные и трудоемкие задачи. С одной стороны, — это решение довольно громоздких уравнений, которые получаются в математической модели при стремлении отразить реальную механическую сущность рассматриваемой проблемы; с другой стороны, — отсутствие для решения полученных уравнений подходящих универсальных
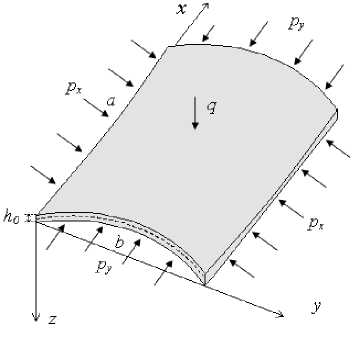
Рис. 1. Вязкоупругая цилиндрическая панель переменной толщины
численных методов и, как следствие, единых вычислительных алгоритмов. Широкое применение персональных компьютеров способствовало появлению программных продуктов для расчета пластин и оболочек переменной толщины и все большему использованию численных методов.
Для получения более адекватной картины напряженно-деформированного состояния тонкостенных элементов конструкций переменной толщины необходимо проводить исследования одновременно и в геометрически нелинейной постановке, и с учетом вязкоупругих свойств материала. Однако анализ доступных авторам источников информации показал, что исследования колебаний и динамической устойчивости указанных элементов с учетом вязкоупругих свойств в рамках нелинейных подходов почти не встречаются.
В данной работе рассматриваются нелинейные колебания вязкоупругой цилиндрической панели со сторонами a и b и радиусом кривизны срединной поверхности R в геометрически нелинейной постановке на основе гипотезы
Кирхгофа-Лява. Панель имеет переменную толщину h = h (x, y), изготовлена из однородного изотропного вязкоупругого материала и нагружена внешними силами px , py и q , означающими интенсивность заданных внешних нагрузок, приложенных к элементу, соответственно, в направлении x, y и z (Рис. 1).
Подробный вывод уравнений математической модели этой задачи осуществляется в работе [8], поэтому здесь приводится только окончательная система интегро-дифференциальных уравнений относительно прогиба w = w ( t, x, y ) и перемещений u = u ( t, x, y ) , v = v ( t, x, y ) [8]:
(1 —Г -) J h Г 8 2 ^
v ’ I 8 x 2
^^^^^^B
1 8 w 1 — ц 8 2 u 1 + ц 8 2 v 8 w 8 2 w 1 — ц8 w 8 2 w 1 + ц8 w 8 2 w
R 8 x 2 8 y 2 2 8 x 8 y 8 x 8 x 2 2 8 x 8 y 2
+
8 h Г8 u 8 v 1 1 ( 8 w 1 2 ц ( 8 w 1
+--+ ц--ц— w + -| — I + | I
8 x _ 8 x 8 y R 2 (8 x J 2 (8 y J
I 1 — Г * ) ! h rf 2 v
I _8 y
—
1 8 w 1 — ц8 2 v 1
R 8 y 2 8 x 2
8 h Г 8 v 8 u 1 1 ( 8 w 1
+ +ц--- w +—|
8 y _ 8 y 8 x R 2 (8 y
—
—
1 — ц 8 h (8 u 8 v 8 w 8 w 11
+---1--1---1---| > + p
2 8 y (8 y 8 x 8 x 8 y JI
1 + ц 8 2 u
+ —---+
2 8 y 8 x 8 y _
( 1 — ц 2 ) p h 8 2 u
—
E 8 1 2
= 0,
8 w 8 2 w 1 — ц8 w 8 2 w 1 + ц8 w 8 2 w + ^-— ■
2 8 x 8 y 8 y 8 y
2 8 y 8 x 2
+
ц( 8 w Y
+ I I
2 (8 x J
— r*^3 (84w 84w8
( ) (8x4 8x28y2
+6 (1 — г* ) h 2 ^h (82w + -' ' 8x (8x3<
*1 L,(8 h Y , 2 82 h
+311 — Г I 2 h — + h —7
v ’ (8 y J 8 y 2
! э л r * , 1 8 u 1 8 v 1
12 ( 1 — Г ) h ц--- 1-----:
v 7 R 8 x R 8 y R'
1 — ц 8 2 u
+---7
2 8 y 2
+S|^ w 1
2 ( 8 y J
1 — ц 8 h (8 u 8 v 8 w 8 w 11
+---1--1---1---I ? + p
2 8 x (8 y 8 x 8 x 8 y JI
2 8 x 8 x 8 y _
( 1 — ц 2 ) p h 8 2 v
—
E 8 1 2
= 0,
। + h 2
8 x
8 2 w
8 2 w
—т + ц +
8 x 2 8 y 2 J
8 3 w ) 8 h (8 3 w 8 3 w )
----2- | + 6 ( 1 — Г ) h |—3- + —2 — | + 8 x 8 y 2 J x ’ 8 y (8 y 3 8 x2 8 y J
8 w 82 w ) , x/ .4 8 h 8 h 2 82 h 8 w —2- + ц —2- I + 6 ( 1 — ц ) ( 1 — Г ) 2 h --+ h2--
8 y 2 8 x 2 J ' 7_ 8 x 8 y 8 x 8 y J8 x 8 y
1 ( 8 w 1 2 1 ( 8 w 1
—— I I +—I I
2 R (8 x J R (8 y J
—
12 ^ ( 1 — Г * ) J h ^
8x ' 71 8x 2
—
—
1 8 w ц +
R 8 x
1 + ц 8 2 v 8 w 8 2 w 1 — ц8 w 8 2 w 1 + ц8 w 8 2 w
+----1---+----+----
2 8 x 8 y 8 x 8 x 2 2 8 x 8 y 2 2 8 y 8 x 8 y
1 — ц 8 h (8 u 8 v 8 w 8 w
+---I--1---1---
2 8 y (8 y 8 x 8 x 8 y
—
—
12 ^ w (1-Г-)l h ^^ 8 y' 71 _8 y 2
8 2 v
8 y
—
8 h
+--
8 x
8 u 8 v 1 1 ( 8 w 1 2
+ ц —ц w + I I + 8 x 8 y R 2 (8 x J
n 82 wh г*1 /Г5 u, 8 v
12 ——11 — Г ) h --+ ц-- ц
8 x 2V 7 _8 y 8 y
1 1 ( 8 w Y ц ( 8 w 1
— w + +
R 2 (8 x J 2 (8 y J
1 8 w 1 — ц8 2 v 1 + ц 8 2 u 8 w 8 2 w 1 — ц8 w 8 2 w
12- +12- +2- + R 8 y 2 8 x 2 2 8 x 8 y 8 y 8 y 2 2 8 y 8 x 2
—
1 + ц d w 8 2 w + —---
2 8 x 8 x 8 y
d h 8 v 8 u 1
1 ( d w )
+--— + ц---w +—I — dy ^dy 8x R 2 (dy
uf d w Y + Я — I
2 ( d x J
1 - u d h (8 u 8 v 8 w 8 w ) I
+---I--1---1---I I —
2 8 x (d y 8 x 8 x 8 y J
—
n 52 wh 5 v . d u 1 1 (8 w Y
12 — -( 1 — Г ) h — + ц--- w +—I— |
8 y 2 ' L 8 y 8 y R 2 ( 8 y J
8 2 w
—
8 y
uf d w Y
+-9I — I 2 ( 8 x J
—
, x 8 2 w „.\,fd u 8 v 8 w 8 w ) 12 ( 1 ц ) р h d2 w
— 12 ( 1 — ц )---- ( 1 — Г ) h I — + — +-- I +— --------v
2 d x 8 yv ' (d y 8 x 8 x 8 y J E 8 t
12 ( 1 — Ц 2 )
E q ,
где Г* — интегральный оператор с ядром релаксации Г ( t ) , действующий на функцию 9 :
t
Г * 9 = | г ( t — т ) 9 ( т ) d т , t — время наблюдения; т — время, предшествующее моменту наблюдения;
ц — коэффициент Пуассона; E — модуль упругости; р — плотность материала.
Пусть закон изменения толщины имеет следующий вид [6]: h = h 0 ( 1 + а * ( б ( x / а ) 2 — 6 ( xj а ) + 1 ) ) , а * — параметр, характеризующий интенсивность изменения толщины, h 0 = h ( 0 ) = const — толщина панели, соответствующая а * = 0. Приближенное решение системы (1) будем искать в виде:
NM NM NM u ( t, x, У ) = LL unm ( t )ф nm ( x, У ) , v ( t, x, У ) = LL vnm ( t )Ф nm ( x, У ) , w ( t, x, У ) = LL wnm ( t ) ^ nm ( x, У ) , (2)
n = 1 m = 1 n = 1 m = 1 n = 1 m = 1
где u nm = u nm ( t ) , v nm = v nm ( t ) , w nm = w nm ( t ) — неизвестные функции времени; 0 nm ( x , У ) , ф nm ( X , У ) , V nm ( x , y ) — координатные функции, удовлетворяющие заданным граничным условиям задачи ( n = 1,2,..., N ; m = 1,2,..., M ).
Подставим (2) в систему (1) и применим метод Бубнова-Галеркина (при px = py = 0). При этом введем следующие безразмерные величины: u/h 0 ; v/h 0; w/h 0; x/a ; y/b ; ю t ( ю = д/п4 Eh 0 2 /(_ 3 р b 4 ( 1 — ц 2 )) — частота основного тона колебаний упругой панели); ky = b 2 /( h 0 R ) ; h/h 0; ( q/E ) ■ ( b/h 0 ) 4 ; X = a/b ; 5 = b/h 0 . Тогда для определения неизвестных unm = unm ( t ) , vnm = vnm ( t ) , wnm = wnm ( t ) получим следующую систему нелинейных интегро-дифференциальных уравнений:
NM
W a,, u k ln m nm
n = 1 m = 1
.J NM (
— П 1 ( 1 — Г ) i ZE l d 1 k ln m u nm +X e 1 k ln m v nm I n = 1 m = 1 (
—
^ц ky f Y 1 V M In flklnmwnm | + tL L g 1 klnmijwnmwj Г = 0, o J 0 n, i=1 m, j=1
NM
УУb, v klnm nm n=1 m=1
[ N M fl
-nYl-r’)
| n = 1 m = 1 (^
+ е^м v
2 k ln m nm
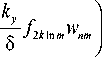
+ f 3 k ln m w nm
1 NM
8 / v / к g 2 k ln mi j nm ^jij n , i = 1 m , j = 1
= 0,
NM
У У c,, w klnm nm n=1 m=1
I N M
+n.
(1
—
г’)
<У
d4
I n = 1 m = 1
+ е^м v
3 k ln m nm
NM
)— У У g i/> • w w..
g3klnmi j nm ij n, i=1 m, j=1
—n 3 ' L LL w nm ( 1 — Г * ) ( d 4 k ln mij u j + e 4 k ln mijVi + f t k ln mij w i ) + L ^L g k ln mijrs w nm ( 1 — Г j w ij w rs ^ = 12 П 3 ( 1 — Y ) ^ 4 q« ,
I n , i = 1 m , j = 1 n , i , r = 1 m , j , s = 1
unm (0)= u 0 nm , utnm (0) = ^<0 nm , vnm (0) = v0 nm , vnm (0) = v0 nm , wnm (0) = w0 nm , 'wnm (0) = 'w0 nm (k = U"., N, 1 = I2,",M ) , где n1 30 /(п X ) ; n2 = 30 /п ; n3 1 (4п X ) ; ak!nm , bklnm , cklnm , d 1 klnm , d2klnm , d3klnm d4klnmij , e1 klnm , e2klnm e3k ln m,
e 4 k ln mij ,
f 1 k ln m ,
f 2 k ln m ,
f 3 k ln m ,
f 4 k ln m ,
g 1 k ln
mij ,
g 2 k ln mij ,
g 3 k ln mij , g k ln mijrs , q kl
безразмерные
коэффициенты, связанные с координатными функциями и их производными; точки над переменной означают взятие производной по времени соответствующего порядка.
Отметим, что начальным моментом колебательного процесса является статическое равновесное состояние панели под нагрузкой q. В этом состоянии панель представляет собой изогнутую поверхность w(0, x, y), поэтому для нахождения w0nm решается соответствующая упругая нелинейная статическая задача. Найденные прогибы панели будут служить начальным приближением для решения соответствующей вязкоупругой нелинейной динамической задачи.
Пусть панель шарнирно оперта по контуру. Граничные условия будут иметь вид [9]: w L= о = 0, v L = 0 = 0, x = 1 X = 1
N x l x = о = 0, M x l x = о = 0, w L = 0 = 0 , u\ y = o = 0, N y = 0 = 0, M y = 0 = 0, где M x , M — изгибающие моменты, Nx ,
X = 1 'x = 1 'y = 1 'y = 1 y l y = 1 y l y = 1 y
Ny — перерезывающие усилия в направлении осей x и y [8]. Тогда в разложении метода Бубнова–Галеркина (2) функции v nm ( x , y ), ф nm ( x , y ) и ф nm ( x , y ), удовлетворяющие заданным граничным условиям, соответственно представляются в виде: v nm ( x , y ) = sin п n x sin m n y , ф nm ( x , y ) = cos п n x sin m n y , ф nm ( x , y ) = sin п n x cos m n y .
Интегрирование уравнений (3), полученных на основе представления решения в форме (2) с учетом различных факторов, выполнялось с помощью численного метода, основанного на исключении особенности в ядре релаксации интегрального оператора [10]. Этот метод был распространен на системы интегро-дифференциальных уравнений, не разрешенных относительно старших производных [11]. При этом в расчетах использовались слабосингулярные ядра релаксации Колтунова–Ржаницына [12]:
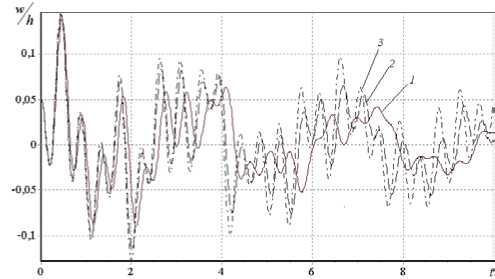
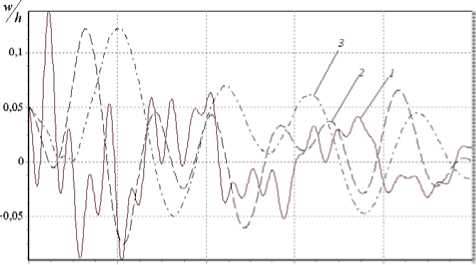
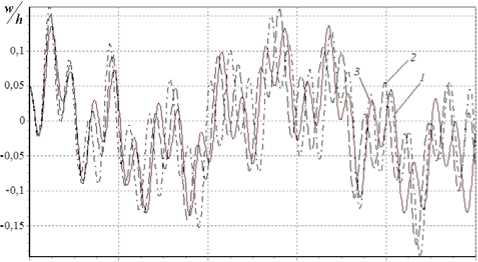
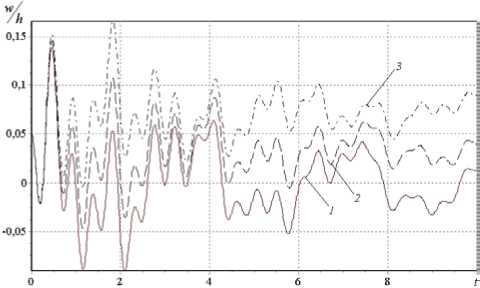
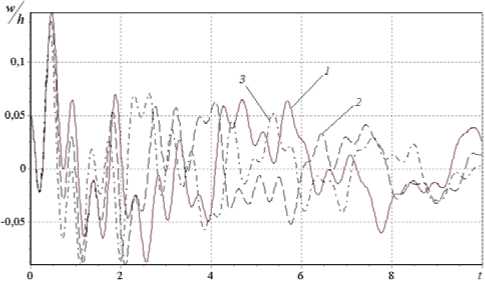
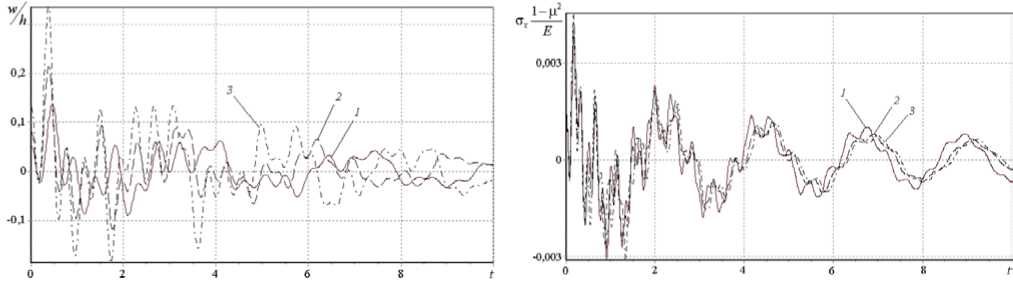
Г(t) = Ae't ■ ta—1, (А > 0, p> 0,0 Подставляя выражение (4) в систему (3) и дважды интегрируя её по времени t , получим следующую систему взаимосвязанных интегральных уравнений N M N M t t I N M — уЦky ] . f 1 klnmWnm | + 0 У УУaM u =\Уам (un + ги t) +n ШУУ 1 — Г* d„. u +Xe,. v k ln m nm k ln my 0 nm 0 nm ) 11 J / 1 k ln m nm 1 k ln mnm n=1 m=1 n=1 m=1 0 0 I n=1 m=1 NM +1 LLg1k ln mij(1—r*) wmwjr dт dт, 0 n, i=1 m, j=1 NM LL bk ln m v nm NM LL bk ln m ( V0 nm —k^f™ 6 J 2 k In m t t Г N M/ + V„ A + n, H W(1 — Г*| d^ u + e v 0 nm / I 2 1 J у yi a 2 k ln m nm 2 k ln m nm 0 0 | n=1 m=1 1 N M] w + —У У g.,,, (1 — Г* |w w.3dтdt, nm g2k ln mij nm ij, ) 0 n, i=1 m, j=1 — NM cw klnm nm N M t t Г N M = LL ckhm ( W0 nm + w0 nmt ) —П 3 fflLL(1 — Г )( d3 khmunm + e3 kln mVnm + n=1 m=1 00 | n=1 m=1 NMNM + fit w — g^/i |1 — Г )w w.. — w [1 — Г Hd,.;! .u.. + елмv 3klnm nm g3k ln mij nm ij nm 4klnmij ij 4kln mij ij n, i=1 m, j=1 n, i =1 m, j=1 N MI +f4 k In mij wjj)—L L gklnmijrswnm (1 — Г )wjw,s —12(1 — Ц )^'9k/ [ dTdT, n, i, r=1 m, j, s =1 и (0) = n nm 0nm ulnm (0)= u0nm V„m (0) = V0nm , 1^nm (0) = !^0nm , w„m (0) = w0nm , I1nm (0) = I10nm (k = 1,2, N, I = 1,2,...,M). Заменяя двойной интеграл одинарным, систему (5) перепишем в виде: N M N M t Г N M 77 a,, u =7 7 a,, uu,, + zi„ t) +n tt — тк/ / 11 — Г )(d,,, u +Xe,,,v k ln m nm k ln m \ 0 nm 0 nm ) *1 J V / I у J \ 1 k In m nm 1 k In m nm n=1 m =1 n=1 m=1 0 I n=1 m=1 ^Цky ) 1 N M (*\ I y-j\ k ln mwnm |+^L L g 1 k ln mij (1 — Г ) wnmwij Г d T, 0 у 0 n, i=1 m, j=1 NM bv klnm nm n=1 m=1 N M t Г N M / 1 = LL Ьк ln m ( V 0 nm+ V0 nmt ) +П J( t— ThLL(1 — Г* )i Td 2 kln munm+e 2 kln mVnm n=1 m=1 0 I n=1 m=1 \ ^ — k 1 1 N M -/»! w l + 1У У g„, 5 J 2 k ln m nm ° 2 k ln my у 0 n, i=1 m, j=1 N M N M t Г N M LL ck ln mwnm =LL ck lnm ( w0 nm+^^0 nmt ) —П 3 J( t—t^LL^ — Г* )( d 3 kln munm+e3 kln mVnm+ n=1 m=1 n=1 m =1 0 I n=1 m=1 NMNM +f3 k In mwnmHZg3kInmij (1 Г ) wnmwij J J J j wnm (1 Г )(d4kInmijuij + e4kInmij^ij + n, I=1 m, j=1 n, i=1 m, j=1 N M1 +f4 k In mijwij ) — J J gk ln mijrswnm (1 Г) wjwrs — 12(1 V )^ qu [ dT, n, i, r=1 m, j, s=1 u (0) = un , U (0) = un , v (0) = vn , v (0) = vn , nm 0nm , nm 0nm , nm 0nm , nm0 wnm (0) = W0 nm , wnm (0) = w0 nm (k = 1,2,..., N, l = 1,2,..., M). Далее осуществляем регуляризацию системы нелинейных интегро-дифференциальных уравнений (6) с сингулярным ядром релаксации Колтунова-Ржаницына (4). С помощью замены переменных t -t = z1“, t 0 < z< ta, 0 1 интеграл вида A J( t -t)“1e-e(t-t)w (t) d t от выражения, содержащего ядро Колтунова-0 A t “ Ржаницына с особенностью, запишется как —j eez w(t - z1“) dz . Теперь подынтегральная функция a 0 становится регулярной относительно z. Далее, полагая t = ti, ti = iAt, (i = 1, 2,...; At — шаг интегрирования) и заменяя интегралы квадратурными формулами трапеций, получим систему рекуррентных формул для вычисления неизвестных uinm = uinm (ti), vinm = vinm (ti) и winm = winm (ti). Погрешность численного метода совпадает с погрешностью использованных квадратурных формул и имеет тот же порядок малости относительно шага интерполяции [10, 11]. Одним из важных этапов решения нелинейных задач является исследование сходимости итерационного процесса на каждом шаге интегрирования по времени. В данной работе для выполнения этой задачи был разработан следующий алгоритм: 1. При заданных граничных условиях решается линейная задача. Определяются значения прогибов и перемещений. 2. Проверяется условие (1/200) <(h0 /lmin )<(^8) (lmin= min {a,b}). Если оно выполняется, то 3. Сравниваются значения максимальных прогибов wmax с толщиной h0. Если (wmax/h0)<(V4), далее реализуется пункт 6; в противном случае — пункт 4, начальными условиями при этом служат найденные значения прогибов и перемещений. 4. На основе полученных значений прогибов и перемещений, которые подставляются в правую часть уравнений (6), решается нелинейная задача. Вычисляются значения прогибов и перемещений с учетом нелинейности. 5. На поверхности панели находятся max {w(k)} , max {Mx(k)}, max {My(k)} ; здесь k — номер текущей 6. Вычисляются значения внутренних усилий и моментов, и выполняется следующий шаг интегрирования. осуществляется переход к следующему пункту; в противном случае варьированием параметра интенсивности изменения толщины сначала достигается выполнение этого условия, а потом делается переход к следующему пункту. итерации. Исходя из наперед заданной точности е1, б2 (заданные малые числа) полученные значения сравниваются со значениями, вычисленными на предыдущей итерации: |w(k) - wk_1)| Далее приводятся результаты вычислений, выполненных на основе представленного алгоритма при различных физических и геометрических параметрах вязкоупругой цилиндрической панели. Если условия не оговорены особо, то в качестве исходных данных при вычислениях используются следующие параметры ядра (4): A = 0,05; a = 0,25; в = 0,05, геометрические параметры a* = 0,5, 5 = 25, ky = 20, Х = 1, а также коэффициент Пуассона ц = 0,3 и статическая поперечная нагрузка q = 0 . Расчеты показали, что при решении данных задач в разложении метода Бубнова–Галеркина достаточно удерживать 25 первых гармоник (N = 5, M = 5), так как дальнейшее увеличение количества членов не оказывает существенного влияния на амплитуду колебания вязкоупругой панели. На рисунке 2 представлена зависимость от времени прогиба срединной точки панели при различных значениях параметра A: A = 0 — упругая модель; A = 0,05 и 0,1 — вязкоупругая модель. Как и ожидалось, учет вязкоупругих свойств материала панели приводит к затуханию колебательного процесса, при этом, хотя решение упругой и вязкоупругой задач в начальный период времени мало отличаются друг от друга, с течением времени отличие становится существенным. Роль в колебательном процессе других параметров демонстрируют рисунки 3-9. Влияние реологического параметра а показано на рисунке 3. Из рисунка видно, что его увеличение приводит к росту амплитуды и частоты колебаний. Расчеты показали, что изменение параметра в (0 < в < 1) не оказывает существенного влияния на процесс колебаний вязкоупругой панели. Увеличение геометрического параметра X (Рис. 4) приводит к уменьшению частоты колебаний. С ростом параметра а* (то есть с утолщением панели к периферии) наблюдается увеличение максимальных перемещений (Рис. 5). Решаемая задача и численный алгоритм достаточно сложны, поэтому для подтверждения достоверности полученных результатов на этом рисунке для сравнения приводятся результаты из работы [9]. Анализ графиков показывает, что результаты решения задачи для упругой панели постоянной толщины (кривая 1) точно совпадают с результатами работы [9]. Аналогичный вывод следует и из сравнения расчетных данных для вязкоупругих панелей постоянной толщины с данными работы [13]. Из рисунка 6 видно, что изменение q не влияет на частоту колебаний. Отметим, что с её увеличением амплитуда пропорционально возрастает и наоборот. На рисунке 7 показаны результаты расчета колебаний срединной точки панели при различных значениях геометрического параметра ky. Увеличение ky (что соответствует увеличению одной из сторон панели или уменьшению радиуса кривизны срединной поверхности и толщины панели) вызывает уменьшение амплитуды колебаний и заметное уменьшение частоты колебаний. О i 4 6 S t Рис. 2. Зависимость прогиба от времени при различных значениях параметра ядра A : 0 (кривая 1), 0,05 (2), 0,1 (3) Рис. 3. Зависимость прогиба от времени при различных значениях параметра ядра а : 0,25 (кривая 1), 0,5 (2), 0,75 (3) О 2 4 б 8 Г Рис. 4. Зависимость прогиба от времени при различных X: 1 (кривая 1); 2 (2); 3 (3) 0 2 4 6 8 / Рис. 5. Зависимость прогиба от времени при различных а*: 0 (кривая 1), 0,3 (2), 0,5 (3) Рис. 6. Зависимость прогиба от времени при различных q : 0 (кривая 1); 1 (2); 2 (3) Рис. 7. Зависимость прогиба от времени при различных ky: 10 (кривая 1); 20 (2); 30 (3) Результаты, полученные при различных условиях на границах панели (либо шарнирное опирание, либо защемление), содержит рисунок 8. В случае, когда две противоположные стороны шарнирно оперты (при у = 0 dw и 1), а две другие жестко защемлены (при x = 0 и 1), граничные условия имеют вид: wx=о = 0, — = 0, x=1 dx x=0 x=1 vlx=0 = 0 , Nxlx=0 = 0. Тогда в разложении метода Бубнова-Галеркина (2) аппроксимирующие функции прогиба x=1 x=1 Vnm (x, У) представляются как балочные функции Крылова [14, 15] vnm (x, y) = Xn (x)sin mпy, где X„(x) = sin X„ x - shX„ x - a (cos X„ x - chX„ x), a„ = (sin X - shX„)/(cos X - chX„), X = (2 n +1) п/2. n n nn n n, n nn nn, n При жестком защемлении всей границы панели [9] wx=0 x=1 dw дx x=0 x=1 = 0, v|x=0 = 0, Nx| x=1 1 x=0 x=1 = 0; wy =0 = 0 , У=1 dw dy y=0 У=1 = 0, u\y=0 y=1 = 0 , Nyy=0= 0 . В этом случае аппроксимирующие функции прогиба y=1 V nm ( x, У ) выглядят следующим образом: V nm ( x, У ) = Xn ( x) Xm ( y ) , где Xm ( У ) = sin Xmy-shXmy-am (cos Xmy-chXmy ) , am =(sin X m - shX m)/(cos X m - chX m), X m =( 2 m + 1)п/2. Анализ полученных результатов показывает, что c увеличением количества защемленных сторон частота колебаний панели увеличивается. Помимо прогибов и перемещений панели, представляют интерес напряжения, моменты и перерезывающие силы. На рисунке 9 представлена зависимость от времени безразмерной функции стx [8]: СТ x dv kx + цX2ky — X5 1 (дw ] Xц(дw I I +—I X5 ( дx J 5 ( дy Анализ полученных результатов показывает, что увеличение параметра а приводит к уменьшению амплитуды напряжений. Рис. 8. Зависимость прогиба от времени и граничных условий: кривая 1 – все стороны панели шарнирно оперты; 2 – шарнирно оперты две противоположные стороны, а две другие жестко защемлены; 3 — все стороны жестко защемлены Рис. 9. Зависимость напряжения стx от времени при разных а*: 0 (кривая 1), 0,3 (2), 0,5 (3) Выводы В работе предложен метод исследования геометрически нелинейных колебаний вязкоупругих круговых цилиндрических панелей переменной толщины. Исследовано влияние на колебания различных физикомеханических характеристик и геометрических параметров. Установлено, что учет вязкоупругих свойств элементов несущих конструкций переменной толщины приводит к уменьшению максимальных прогибов. Это объясняется тем, что изменение напряжений по толщине для панелей переменной толщины более значимо, чем для панелей постоянной толщины. Создан программный комплекс, позволяющий при проведении численных экспериментов варьировать действующие на панель внешние силы и нагрузки, тем самым достигать ее оптимальной формы. Предложенный метод может быть использован для пластин, панелей и оболочек переменной толщины и в случае их ортотропных свойств.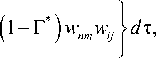
1, MX^k)- M^^Jk_1)|2. Если эти условия выполняются, то следует переход в пункт 6; в противном случае вновь выполняется пункт 4 при k +1.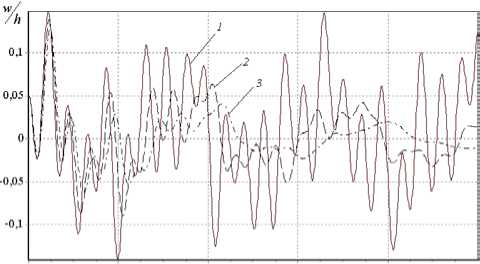
Список литературы Исследование вязкоупругих круговых цилиндрических панелей переменной толщины
- Карпов В.В. Геометрически нелинейные задачи для пластин и оболочек и методы их решения. -М.: Изд.-во АСВ, 1999. -154 с.
- Игнатьев О.В., Карпов В.В., Филатов В.Н. Вариационно-параметрический метод в нелинейной теории оболочек ступенчато-переменной толщины. -Волгоград: ВолГАСА, 2001. -210 с.
- Антоненко Э.В., Хлопцева Н.С. Осесимметричная форма потери устойчивости тонкостенных цилиндров переменной толщины//Математика. Механика: Сб. науч. тр./Саратов: Изд.-во Сарат. Ун-та, 2006. -№ 8. -С. 165-167.
- Габбасов Р.Ф., Мусса Сали, Филатов В.В. Колебания пластин переменной жесткости//Известия вузов. Строительство. -2006. -№ 5. -С. 9-15.
- Абросимов А.А., Филиппов В.Н. Исследование НДС пластин переменной толщины в геометрически нелинейной постановке с разными системами аппроксимирующих функций//Прикладная математика и механика: Сб. науч. тр. Ульянов. гос.-техн. университета/Ульяновск: Изд.-во УлГТУ. -2007. -С. 3-8.
- Будак В.Д., Григоренко А.Я., Пузырев С.В. Решение задачи о свободных колебаниях прямоугольных в плане пологих оболочек переменной толщины//Прикладная механика. -2007. -Т. 43, № 4. -С. 89-99.
- Коренева Е.Б. Аналитические методы расчета пластин переменной толщины и их практические приложения. -М.: Изд-во АСВ, 2009. -240 с.
- Верлань А.Ф., Абдикаримов Р.А., Эшматов Х. Численное моделирование нелинейных задач динамики вязкоупругих систем с переменной жесткостью//Электронное моделирование. -2010. -Т. 32, № 2. -С. 3-14.
- Вольмир А.С. Нелинейная динамика пластинок и оболочек. -М.: Наука, 1972. -432 с.
- Бадалов Ф.Б., Эшматов Х., Юсупов М. О некоторых методах решения систем интегро-дифференциальных уравнений, встречающихся в задачах вязкоупругости//ПММ. -1987. -Т. 51, № 5. -С. 867-871.
- Эшматов Х., Абдикаримов Р.А., Бобоназаров Ш.П. Колебания и устойчивость вязкоупругой трубы с протекающей через нее жидкостью при различных граничных условиях//Узбекский журнал «Проблемы механики». -Ташкент, 1995. -№ 1. -С.20-24.
- Колтунов М.А. Ползучесть и релаксация. -М.: Высшая школа, 1976. -276 с.
- Eshmatov B.Kh., Mukherjee S. Nonlinear vibration of viscoelastic composite cylindrical panels//J. of Vibration and Acoustics. -2007. -V. 129. -P. 285-296.
- Толок В.А. Алгоритмизация расчета цилиндрических оболочек. -Ташкент: Фан, 1969. -121 с.
- Бабаков И.М. Теория колебаний. -М.: Наука, 2004. -592 с.


