Исследование влияния альфвеновского резонанса на основную моду, генерируемую неустойчивостью на магнитопаузе

В системе солнечный ветер – магнитосфера су ществует набор мод собственных колебаний [Mills, Wright, 1999]. При этом нулевая мода системы ( в работе [Taroyan, Erdelyi, 2002] авторами вводится спе циальное название для этой моды «primary mode» – основная мода ) является поверхностной волной на границе раздела солнечный ветер – магнитосфера .

Неустойчивость Кельвина – Гельмгольца на маг нитопаузе является одним из основных источников энергии крупномасштабных колебаний магнито сферы Земли . Порог по скорости солнечного ветра ( V SW ) этой неустойчивости для нулевой , или ос новной , моды из указанного выше набора собст венных мод представляет особый интерес ввиду того , что он достигается при наименьшей скорости солнечного ветра . Это означает , что такая мода МГД - колебаний может присутствовать в магнито сфере регулярно , для этого не требуется особых условий ( большой скорости солнечного ветра ). Еще раз отметим , что нулевая , или основная , мода системы является поверхностной волной на грани це раздела солнечный ветер – магнитосфера .

Благодаря космическому проекту THEMIS, стар товавшему в 2007 г ., стало возможным одновремен ное измерение параметров плазмы сразу во многих точках различных магнитосферных оболочек и в области солнечного ветра . Пять спутников , сле дующие друг за другом , позволяют одновременно измерять амплитуды ULF- волн на некотором отрезке поперек магнитопаузы во время ее пересечения , что является необходимым для наблюдения пространст венной структуры данных волн , поскольку область их локализации может простираться достаточно далеко в солнечный ветер .

Рассматриваемая нами основная мода может возбуждать альфвеновскую волну на резонансной магнитной оболочке, локализованной вблизи магнитопаузы. Более высокие гармоники (с номерами n>0) имеют резонансные оболочки только в глубине магнитосферы [Мазур, Чуйко, 2012]. Для них область магнитосферы, прилегающая к магнитопаузе, является областью прозрачности, а резонансные оболочки расположены в области непрозрачности внутри магнитосферы.

Напомним , что альфвеновский резонанс является диссипативным механизмом для БМЗ - волны . Энер гия БМЗ - волны просачивается в область непрозрач ности и диссипирует в узкой окрестности резонанс ной оболочки .

Анализ экспериментальных данных [Roux, Robert, 2011] показал , что имеется корреляция между нагре вом электронов и ULF- волнами . В качестве меха низмов этого нагрева рассматриваются затухание Ландау [Roux, Robert, 2011], турбулентность [Chas-ton, Bonnell, 2008], стохастическое нагревание кине тическими альфвеновскими волнами [Jay, 2001].

Опираясь на результаты предыдущих работ [ Ма зур , Чуйко , 2011, 2012], в настоящей работе мы ис следуем возможность нагрева плазмы магнитопау зы . Механизм нагрева состоит в следующем . Кине тическая энергия солнечного ветра переходит в энергию колебаний основной моды посредством неустойчивости Кельвина – Гельмгольца . Энергия основной моды может диссипировать в магнито сферной части переходного слоя , близкой к магни топаузе , – в области альфвеновского резонанса .

Модель среды

Схематическое изображение фланговой области магнитосферы и прилегающей к ней части солнеч ного ветра , а также используемая нами одномерная модель этих областей представлены на рис . 1. Из этого рисунка видно соответствие между различны ми элементами модели и реальной системы . Будем полагать , что в полупространстве , отвечающем маг нитосфере , плазма холодная , так что скоростью зву ка с _S можно пренебречь по сравнению со скоростью Альфвена c A ( характерное значение β M =0.5), и на против , плазму в полупространстве солнечного ветра будем считать горячей и пренебрегать ско ростью Альфвена по сравнению со скоростью звука ( плазменное β солнечного ветра зависит от солнечной активности , но остается большим единицы ,

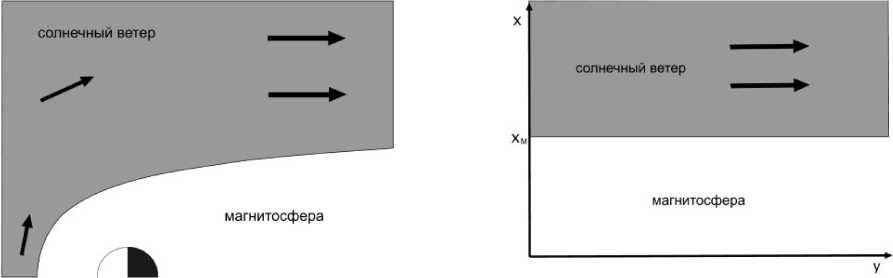
Рис . 1 . Соответствие элементов реальной среды и используемой одномерно - неоднородной модели .

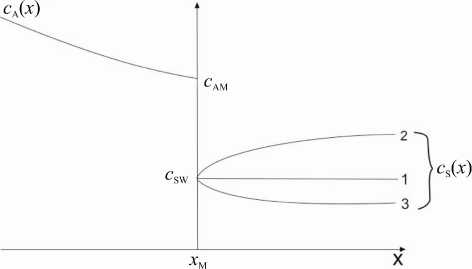
Рис . 2 . Зависимость от координаты х скорости Альф - вена с _А ( х ) в магнитосфере . Точка х = х _М – координата маг нитопаузы .

хотя при некоторых условиях ненамного ). Послед нее предположение означает , что наличием магнит ного поля в солнечном ветре можно пренебречь .

На рис . 2 представлен схематический график зави симости от x скорости Альфвена в магнитосфере и скорости звука в солнечном ветре . Монотонная зави симость c A ( x ) означает , что мы игнорируем наличие мелких структурных элементов магнитосферы . На интересующие нас колебания глобального масштаба такие структурные элементы не оказывают сущест венного влияния . Мы также игнорируем существова ние плазмосферы , поскольку плазмосфера находится глубоко в области непрозрачности рассматриваемого набора собственных мод . Будем считать , что магнито сферное магнитное поле B M направлено по оси Z. Ус ловие равновесия плазмы , следующее из уравнений идеальной МГД , имеет вид

^ ^ ^    ^ ^

ρU ⋅∇U = J ×BM c

-

v B M ,

8 π

^

где ρ – плотность плазмы , U – средняя скорость ее глобального движения , J – ток , протекающий в плазме , c – скорость света в вакууме . Пренебрегая наличием глобальных токов ( J ) и глобального движения плазмы ( U ) , получаем

V BM- = 0, 8π откуда следует BM=const.

В работе [Jay, 2001] показано, что в неустойчивом режиме набор собственных мод системы сол- нечный ветер–магнитосфера не зависит от выбора модели солнечного ветра (см. рис. 2), поскольку характерный масштаб колебаний в солнечном ветре много меньше масштаба неоднородности плазмы. Следовательно, результаты настоящей работы применимы для всех трех моделей среды, показанных на рис. 2.

Нулевая (основная) мода

В описанной выше модели существует набор соб ственных мод резонатора [ Мазур , Чуйко , 2011]. При различных профилях скорости солнечного ветра в переходном слое гармоническая структура собствен ных мод может частично распространяться в область солнечного ветра . При этом нулевая , или основная , мода системы является поверхностной волной на границе раздела солнечный ветер – магнитосфера . Для существования основной моды рассматриваемо го резонатора необходимо наличие сдвигового тече ния солнечного ветра ( см . работу [ Мазур , Чуйко , 2012]). В рассматриваемой нами задаче собственные моды черпают энергию из сдвигового течения на магнитопаузе из - за развивающейся в нем неустойчи вости Кельвина – Гельмгольца . При этом только нуле вая мода является поверхностной волной на границе раздела солнечный ветер – магнитосфера . Это значит , что и магнитосфера , и солнечный ветер являются об ластями непрозрачности для нулевой моды и при оп ределенных условиях на магнитопаузе появляется ин тересующий нас альфвеновский резонанс . В рассмат риваемой одномерно - неоднородной модели среды с прямыми силовыми линиями геомагнитного поля эти условия выполняются . Альфвеновский резонанс лока лизован в точке x _A, определяемой из условия

ω cA(xA)= . kz

В работе [ Мазур , Чуйко , 2012] нами исследовалось влияние альфвеновского резонанса на моды с номером выше нулевой , для которых резонанс находился в глу бине магнитосферы . Здесь же мы исследуем случай , когда и альфвеновский резонанс , и скачок параметров плазмы расположены вблизи магнитопаузы .

Влияние альфвеновского резонанса на нулевую моду

Зависимость проекции ξ x вектора смещения плазмы от координат ( x , y , z ) и времени ( t ) выберем в виде

ξ _x ( x , y , z , t ) =ξ _x ( x )exp( ik_yy + ik_zz - i ω t ), где ω – частота волны . Другие возмущенные вели чины имеют аналогичную зависимость .

Уравнение , описывающее структуру колебания по координате x , в приближении идеальной МГД имеет вид [Duhau, Gratton, 1975]

d ρ Ω2 dξ

⁰ ₂ ^{A    x} + ρ ₀ Ω ² _A ξ _x = 0.

dx K ² dx

Здесь ρ ₀ = ρ ₀ ( x ) – плотность плазмы ,

Ω ² A = ω ² - kz ² c A ², ω =ω- ktV SW , kt = (0, ky , kz ),

22 при u <  u _A ,

2 I 1 (

A

A

^I 0 ⁽

σ

-

σ

A

) + ⁱ K 1 ( ^{u 2} π

^u A ²

σ

) - ⁱ K 0 ( ^u π

-

)

u _A

σ

)

K ²

ω ⁴

ω ²( c _A ² + c _S²) - k_z ² c _A ² c _S ²

- k ², k ² = k ² + k ². yz

В дальнейшем мы будем вместо смещения ξ x ис пользовать функцию

ς ( x ) =- ρ ^{0 Ω} 2 ^{2A d ξ x}

_K 2 _dx

.

Ее уравнение имеет вид d2ς - dlnρ0Ω2A dς+K2ς=0.

dx ²       dx dx

Через функцию ς ( x ) можно выразить все возмущен ные величины . В частности , для смещения плазмы и полного возмущенного давления ( суммы газокине тического ( p ) и магнитного ) имеем

ξ = 1  dς x2, ρ0ΩA dx

BB

P = p + ^{0 z} = ς ( x ).

4π

Граничные условия для уравнения (1) при x → ± ∞ в области непрозрачности сводятся к требованию ог раниченности решения . На магнитопаузе , x = x M , ко эффициенты уравнения (1) изменяются скачком . Из этого уравнения следуют условия сшивки

{ ς } _xM = 0,

1 d ς

^ρ 0 ^{Ω 2} A ^dx

= 0,

где символ { f } _{x M} означает скачок величины f в

точке x M .

Дисперсионное соотношение получается из ус ловий сшивки . Пользуясь результатами работ [ Ма зур , Чуйко , 2011; Мазур , 2010], определяем левую f M ( u ) ( магнитосферную ) и правую f _W(w) ( солнеч но - ветровую ) части дисперсионного соотношения вблизи прежнего ( без учета альфвеновского резо нанса ) порогового значения приведенной частоты и .

Если | u ² - u _A² | << 1, то

2 f _M ( u ) =

2 u

-

u

2 ^K 1⁽

A

σ

)

-

^u A K 0 (

u _A

σ

)

при u ² >  u _A² , где σ =    ^{u A}   ( k_tl _M ) ^{- 1},

1 - u _A

u _A

kz

. k_t

Для функции f _W ( w ) используем выражение

f _W (w) =

1 - w²

которое получается в модели однородного солнеч ного ветра . Для моделей с неоднородным солнеч ным ветром оно применимо во всей комплексной

плоскости w за исключением узких полос , которые были рассмотрены в работе [ Мазур , Чуйко , 2011] и находятся вдали от значений w, характерных для

полученного нами решения . Введем обозначения

2   2           77

_{ξ =} u - u _{A ,} ν ₌ u _{A (} V _SW ⋅ k_{t -}

2 σ         σ k_t c _AM

2 α ² u ²

ε2 =        A =1, η=,

γ σ 1 - uA2

_{2 ξ} K 1 ( - 2 ξ ) K 0 ( - 2 ξ ) ^,

если ξ < 0,

φ ( ξ ) =

1    1 , (2 ; ) + -к , (2 ; )

27--------n-------

I ₀(2 ^ > - ^- K o (2 ^ )

I            n

если ξ > 0,

после чего дисперсионное уравнение f _M ( u ) = f _W (w) принимает вид

φ ( ν + εη ( ξ )) = -η ²( ξ ). (3)

Уравнение (3) можно рассматривать как неявно заданную функцию ξ ( ν ) или , исходя из определений (2), как зависимость приведенной частоты колеба ний от скорости сдвигового течения u (v).

При ν = 0 имеются два решения . Первое реше ние – ξ =0( ϕ (0)=0). Второе решение является кор нем трансцендентного уравнения , которое реша лось методом последовательных приближений . Не приводя громоздких вычислений , с точностью до первого порядка по ξ ( ε ) получаем

ξ =

ε

¹ (ln ¹ )² ε

Отталкиваясь от полученного решения , можно построить решение в некой окрестности точки ν =0. Как видно из рис . 3, вблизи точки ξ =0 выполняется соотношение ξ = ν ( вершина параболы близка к на чалу отсчета ), тогда уравнение (3) имеет решение

ε ² ξ = - exp( -   -γ ),

ν ²

которое очевидно совпадает с первым решением в точке ν =0. Поправка ко второму решению находит ся методом последовательных приближений из со отношения ξ = ν + εη . В результате имеем

ξ = ν- ^ε ₁.                                   (5)

(ln ¹ )² ε

Решения (4) и (5) применимы в малой окрестно сти вблизи ξ =0 при условии

ν <<

ε

¹ (ln ¹ )² ε

Из рис . 3 также видно , что при дальнейшем уве личении ν график правой части (4) находится в та кой области , где он не имеет пересечений с графи ком левой части дисперсионного соотношения , и решение дисперсионного соотношения не имеет вещественных корней , а имеет лишь мнимые корни . В этой области ν корни дисперсионного уравнения комплексные . При ν ≥ ν , где ν – некоторое крити ческое значение , возникает неустойчивость рас сматриваемой основной моды колебаний . Это зна чит , что существует пороговое значение скорости сдвигового течения (v~ V SW см . (2)), ниже которого система устойчива . Возникает вопрос : происходит ли отрыв ветвей параболы -η ² от кривой по оче реди или одновременно . Подробный анализ показы вает , что отрыв происходит одновременно , и дает следующие значения для точки отрыва и пороговой частоты :

ν =

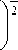
ξ =

ε 3^. 2

2 1 ln- I I e )

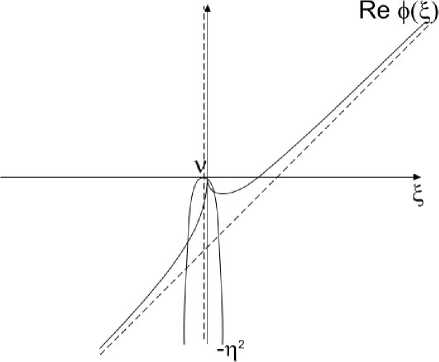
Рис . 3 . Правая и левая части дисперсионного соотноше ния . Пересечение графиков дает вещественное решение .

Найдем теперь продолжения первого и второго решений и получим решение дисперсионного урав нения вблизи порога ( ν >  ν ) . Для этого разложим правую и левую части (3) в ряд Тейлора и сокра тим слагаемые главного порядка теории возмуще ний . В результате получаем

12(-2- ε2φ′′(ξ))(ξ - ξ)2 = 2ν(ν-ν),(6)

откуда

ε2

ξ=ξ±i       (ν-ν)2.(7)

(ln ¹ )⁴ ε

Решение (7) применимо в малой окрестности точки отрыва , такой что

| ν - ν | << ^ε .                                  (8)

(ln ¹ )² ε

Отметим , что решения (5), (6) и (8) определены в неперекрывающихся областях изменения ν . Их , однако , можно соединить плавной переходной функцией и таким образом получить информацию о поведении функции на всем интервале ν ∈ [0, ν ].

Для больших значений параметра ν >> ε | η | можно пренебречь вторым слагаемым в аргументе функции ϕ , и тогда дисперсионное уравнение легко разрешается относительно ξ :

ξ = ν ± ε [ -φ ( ν )]² .

В зависимости от величины аргумента функции ϕ ( ν ) для нее можно использовать различные асим птотические представления :

εε

ξ = ν±        ∓ i π                          (9)

(ln ¹ )²       (ln ¹ )²

νν для ν << ν << 1,

ξ = ν ± ε (2 ν )¹² e ^{- 4 ν} ∓ i ε (2 ν )¹²                     (10)

для 1 << ν << σ .

Таким образом , получено аналитическое реше ние для случая , когда значение приведенной часто ты для нулевой моды близко к пороговому значе нию , или , другими словами , исследована нулевая мода с учетом альфвеновского резонанса . Решения (5), (7), (9), (10) описывают поведение частоты и инкремента нулевой моды для всех возможных зна чений скорости сдвигового течения . При наличии альфвеновского резонанса изменяется порог неус тойчивости , а также зависимость инкремента от скорости солнечного ветра ( ср . с работой [ Мазур , Чуйко , 2011]), однако качественных различий нет . Поэтому наличие альфвеновского резонанса на маг нитопаузе не изменяет характера неустойчивости нулевой моды в зависимости от скорости сдвигово го течения .

Положение альфвеновского резонанса

В зависимости от профиля скорости Альфвена в магнитосфере сА(х) положение точки альфвеновско-го резонанса для нашей модели с прямыми силовыми линиями магнитного поля определяется из соотношения cA(xA) = v cA (xM ) uA

Так , если альфвеновский резонанс находится на магнитопаузе , то v = и А . Из (2) видно , что ν =0 при v = и_А . Решения (4) и (5) вблизи точки v =0 имеют нулевой инкремент .

Заключение

Аналитическое исследование показало, что при определенных условиях кинетическая энергия солнечного ветра трансформируется в энергию неустойчивой поверхностной волны, возбуждаемой на магнитопаузе неустойчивостью Кельвина–Гельмгольца. При наличии вблизи магнитопаузы области альфве-новского резонанса энергия неустойчивых колебаний поверхностной волны переходит в альфвеновскую волну, раскачиваемую на резонансной магнитной оболочке. В области альфвеновского резонанса волновая энергия полностью поглощается, нагревая окружающую плазму. Поэтому происходит нагрев магнитосферной плазмы вблизи магнитопаузы, но не на ней самой. В этом случае инкремент неустойчивости поверхностной волны равен декременту диссипации энергии в области альфвеновского резонанса. В результате создаются условия для появления нейтральной (не растущей и не затухающей со временем) поверхностной моды, распространяющейся по магнитопаузе. Положение резонансной магнитной оболочки для альфвеновской волны и инкремент неустойчивости поверхностной волны определяются скоростью солнечного ветра. Поскольку при наличии альфвеновского резонанса v= иА, основная мода имеет порог неустойчивости при скорости солнечного ветра V≈сА~500 км/с, что близко к типичному значению данной величины.