Исследование влияния двухкомпонентного потока"жидкость-газ" на динамические свойства кориолисова расходомера

Кориолисовы расходомеры широко применяют в самых разных отраслях промышленности для измерения массового расхода текущей однородной и однофазной среды. Успехи в применении кориолисовых расходомеров для решения задач измерения массового расхода однофазных и однородных потоков стимулируют попытки применить их и для измерения объемно-массовых параметров многофазной среды. При этом исследователи отмечают увеличение ошибки измерения массового расхода с ростом объемной доли воздуха в текущей среде. В частности, при попадании воздуха в текущую среду нарушается равномерность распределения флюида по длине измерительной трубки, возрастает демпфирование, что может повлиять на динамические свойства кориолисового расходомера (амплитуды, фазы колебаний и разность фаз, по которой определяется массовый расход).

Многие исследователи пытаются создать способ коррекции ошибки измерения двухфазного потока. В работах [1, 2] подчеркнуто, что фазовый сдвиг, по которому определяется массовый расход, зависит не только от массового расхода жидкости, но и от демпфирования в колебательной системе. В работе [3] предлагается повысить точность измерения расхода текущих жидкостей с пузырьками с помощью измерения скорости звука в технологической жидкости. В работе [4] предлагается повысить точность измерения расхода текущих жидкостей с пузырьками за счет эмпирических зависимостей, связывающих параметры потока двухфазной среды (объемная доля газа в текущей среде, расход среды, давления на входе и на выходе) с величиной массового расхода жидкости, выдаваемой измерительным прибором. В работе [5] указано, что ошибку измерения можно уменьшить путем регулирования коэффициента усиления привода катушки возбуждения.

Однако работ, посвященных исследованию причины снижения точности кориолисова расходомера с применением численного моделирования, не так много. В частности, в работе [6] предложена численная модель прохождения одиночного пузырька газа по прямолинейной трубке, смоделированной балкой Тимошенко, способная качественно описать отклик кориолисова расходомера на присутствие газовых пузырей в потоке жидкости. Но для определения причины увеличения ошибки этого недостаточно.

Наиболее поздняя работа Е. Шавриной [7] посвящена исследованию влияния асимметрии газораспределения на погрешность измерения расхода двухфазного потока «жидкость–газ» кориолисовым расходомером. По результатам конечноэлементных расчетов предлагается коррекция показаний расходомера, учитывающая эффект асимметричного распределения газа по измерительной трубке кориолисового расходомера. В публикации предлагается использовать модель многофазного течения VOF и модель турбулентности рейнольдсовых напряжений RSM. Однако входная граница модели разделена на два сегмента для воды и воздуха. Таким образом, в трубке получается переходный процесс смешивания компонентов, а не развитый двухфазный поток. В другой работе Е. Шавриной [8] выполнен двусторонний анализ кориолисового расходомера – FSI. Но моделирование выполнено для однофазного потока жидкости при кинематическом возбуждении приводной катушки, что приводит к некорректной временной задержке и, соответственно, массовому расходу.

Несмотря на опубликованные в современных статьях результаты исследований, эффект увеличения погрешности измерения кориолисового расходомера, обусловленный попаданием воздуха в текущую жидкость, остается необъясненным.

Таким образом задача создания имитационной модели, учитывающей двухкомпонентный поток «жидкость – газ» и двустороннее взаимодействие «поток–конструкция», является актуальной.

Экспериментальные исследования

Схема проливочного стенда приведена на рис. 1. Стенд состоит из насоса 1 с системой управления 2, бака с водой 3, эталонного кориолисового расходомера (КР) 4 и исследуемого КР 5. При включении насоса 1 происходит подача воды в систему. Текущая вода проходит через эталонный КР 4. Между эталонным и опытным расходомером установлен узел 7, через который с помощью компрессора в текущую жидкость осуществляется подача воздуха. Далее смесь воды и воздуха поступает в исследуемый расходомер 5. Давление на входе и на выходе в опытный расходомер регистрируется датчиками давления. После опытного расходомера смесь попадает в бак 3, в котором естественным путем происходит выведение воздуха из состава флюида и возвраще- ние среды в ее изначальное состояние.

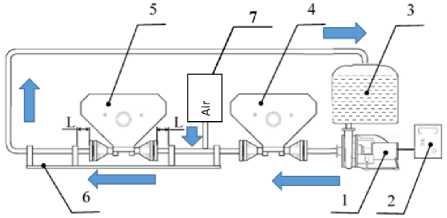
Рис. 1. Схема проливочного стенда: 1 – насос; 2 – система управления; 3 – бак с водой; 4 – эталонный КР; 5 – опытный КР; 6 - оснастка для закрепления исследуемого КР;

7 – устройство для впрыска воздуха в текущую среду

Целью экспериментов являлось сравнение показаний основных характеристик опытного и эталонного расходомера – исследование, необходимое для объяснения влияния газовой фазы на показания опытного расходомера.

Перед началом испытаний при фиксированном массовом расходе воды в 1 т/час ( ∼ 0,3 кг/с) стенд работал в режиме холостого хода, т. е. перекачивал воду (без добавления воздуха) в течение 1,5 ч с целью стабилизации температуры в системе.

Эксперименты проведены при различном массовом расходе жидкости (1040 кг/ч, 1310 кг/ч, 1741 кг/ч), фиксировавшемся по эталонному расходомеру. Каждому расходу жидкости соответствовали 8 разных расходов воздуха. В эксперименте осуществляли запись напряжений с двух измерительных и центральной катушки эталонного и опытного расходомера, а также величин давления в газожидкостной смеси (ГЖС) на входе и выходе на опытном расходомере. Все данные регистрировались системой LMS Scadas Recorder. Длительность каждого эксперимента составляла 45 с.

Механика

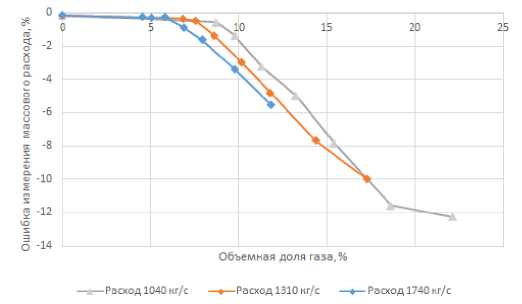
Рис. 2. Величина ошибки измерения массового расхода в зависимости от объемной доли газа

Величину массового расхода жидкости в эксперименте устанавливали по эталонному расходомеру при отсутствии воздуха в системе, затем, когда в текущую через опытный расходомер жидкость попадал воздух, наблюдали снижение массового расхода жидкости на эталонном расходомере. После этого увеличивали частоту насоса до возвращения показаний массового расхода эталонного расходомера, наблюдавшихся при отсутствии воздуха в опытном расходомере. После этого по показаниям датчиков давления на входе и на выходе опытного расходомера, датчиков температуры в расходомерах, показаниям массового расхода эталонного расходомера и объемного расхода воздуха рассчитывали объемные доли воздуха в жидкости (GVF) и по выражению (1) определяли относительную погрешность измерения массового расхода жидкости:

MF - MF

Err_M F =--- оп-----эт • 100 % ,

MF    MFэт где MFоп – показания массового расхода на опытном расходомере; MFэт – массовый расход воды на эталонном расходомере.

В эксперименте наблюдали ошибки измерения массового расхода и плотности на опытном кориолисовом расходомере. Ошибки измерения массового расхода в зависимости от объемной доли воздуха в текущей среде приведены на рис. 2.

Объемные доли воздуха в жидкости GVF (Gas Volume Fraction) рассчитывали по выражению

GVF = Qv ar. , Qv sum

MF T   p где Qv . = —air- • —---0--объемный расход воздуха; Qvsum = Qvfiuid + Qvair — объемный расход air   Pair  T0 P1 + P 0

MF                                   ^p 1 ^{+ p}o

ГЖС; Qv fl _uid = ——— объемный расход жидкости; p_o = ——o-t^ - избыточное давление в ра-

^P fluid                                                   ²

бочих условиях; pi1n – избыточное давление в ГЖС на входе в расходомер; p1out – избыточное давление в ГЖС на выходе из расходомера; T1 = 295,65 K – температура в рабочих условиях; MFair, кг/ч – массовый расход воздуха по показаниям массового расходомера; MFоп, кг/ч – массовый расход ГЖС на опытном расходомере; Pfud = 998,2 кг/м3 - плотность воды при 20 °C; Pair = pair ideal /Z = 1,20445 кг/м3 - плотность воздуха при стандартных условиях (20 °C, 1 атмо- сфера) по ГОСТ 30319.1-96; Z = 0,99963 фактор сжимаемости воздуха; T0 = 293,15 K – температура, соответствующая стандартным условиям; p0 = 101,325 кПа – атмосферное давление.

Численные исследования

Расчетная модель ориентирована на получение количественных оценок влияния потока текущей среды с заданным массовым расходом жидкости и объемной долей воздуха GVF на вынужденные колебания U-образной измерительной трубки кориолисового расходомера.

В рассматриваемом расчетном случае моделируется одна трубка, защемленная с обеих сторон по торцам (рис. 3). Учитывая очень слабое влияние скорости текущей среды на собственные частоты трубки в диапазоне рабочих расходов прибора и очень слабое изменение разности фаз в околорезонансной области, частоту вынуждающего воздействия принимали равной низшей собственной частоте трубки с неподвижной жидкостью при нулевом содержании воздуха.

Например, в статье [8] говорится, что разница между вынужденными и свободными колеба- ниями незначительна и поэтому в качестве вынуждающего воздействия используется кинематическое возбуждение сечения трубки, в котором расположена центральная катушка, и задаются его перемещения по синусоидальному закону с частотой, равной собственной частоте заполнен-

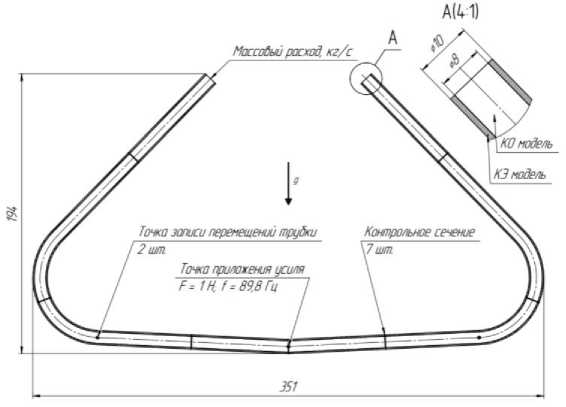
Рис. 3. Расчетная схема 2-way FSI модели

ной трубки с неподвижной средой. Однако в этом случае меняется форма установившихся вынужденных колебаний трубки, при этом форма вынужденных колебаний при таком возбуждении не совпадает с собственной формой вследствие ограничений, накладываемых на углы поворота трубки в сечении, соответствующем центральной катушке. Изменение формы вынужденных колебаний, в свою очередь, приводит к изменению временной задержки. Сопоставление расчетных и экспериментальных временных задержек показывает, что расчетные временные задержки, полученные при кинематическом возбуждении цен- трального сечения, не совпадают с экспериментальными, а расчетные временные задержки, полученные при силовом возбуждении, хорошо совпадают с показаниями опытного расходомера. Поэтому в рассматриваемой модели используется подход, при котором колебания измерительной трубки возбуждаются сосредоточенной силой, направленной перпендикулярно плоскости труб- ки.

Расчет колебательного режима трубки с протекающей по ней жидкостью выполняется как расчет переходного процесса, когда параметры состояния в каждой последующей временной точке используют предварительно найденные (заданные) параметры состояния в предыдущей временной точке. Расчет предусматривает выполнение итерационного анализа поведения жидкости и пошаговое выполнение расчетов во временных точках, соответствующих переходному процессу нарастающих колебаний (вызываемых действием сосредоточенной гармонической вынуждающей силы).

Расчет системы с текущей жидкостью выполняется с использованием двух разных решателей: модуля Transient Structural analysis для расчета трубки и модуля Fluent для расчета потока газожидкостной смеси. Взаимодействие модулей Transient Structural и Fluent реализуется по технологии Two-way FSI и управляется через модуль System Coupling.

Контрольно-объемная модель (КО модель) течения газожидкостной смеси создана в про-грамном пакете ANSYS Fluent. Стратегия численного моделирования двухфазных потоков «газ– жидкость» в трубах выбрана на основе мирового опыта исследователей, изложенного в [9]. Для изучения процесса смешения компонент смеси вода/воздух решено использовать модель Volume of Fluid (VOF). Одно из её достоинств, отмеченное в статье [9], заключается в возможности получения различных режимов потоков.

Модели материалов воды (water-liquid) и воздуха (air) заимствованы из базы данных Fluent. В качестве первичной фазы выбран сжимаемый воздух, вторичной – вода. Поверхностное натяжение (surface tension) установлено постоянным и равным 0,072 Н/м. Реализована острая (sharp) граница раздела фаз. В численной реализации выбор остановлен на модели турбулентности SST.

В качестве входных граничных условий (inlet-water, inlet-gas) заданы массовые расходы воды и воздуха. На выходном отверстии в качестве граничного условия (pressure-outlet) задано избыточное давление, равное 0 МПа. Учтено влияние гравитации в уравнении импульсов, стенки определены как гидравлически гладкие.

С целью анализа распределения воздуха по длине трубки в процессе прохождения среды построено 7 поперечных сечений (см. рис. 3). В каждом сечении записываются значения массового

Механика

расхода смеси, воды и воздуха, а также GVF.

Модель стальной трубки – конечно-элементная модель (КЭ модель) создана в модуле ANSYS Transient, торцы трубки жестко закреплены, а в центральной точке трубки приложено гармоническое силовое воздействие (3) в перпендикулярном плоскости трубки направлении:

F ( t ) = F o sin(2 ^ • f • t ), (3) где t – время, с, f – резонансная частота системы с неподвижной средой (Гц), F 0 – амплитуда силового возбуждения.

По результатам моделирования в контрольных точках № 1 и № 2 (см. рис. 3) строятся графики перемещений точек двух сечений по времени. После этого вычисляется временная задержка по фазовому сдвигу между точками при переходе через нулевое значение.

Время моделирования составляет 0,4 с. Предварительный этап от 0 до 0,2 с заложен для стабилизации временной задержки. Выполнено две серии расчетов с различными значениями объемной доли газа и двумя значениями шага по времени 1·10–4 с и 5·10–5 с. Соответствующие виброграммы приведены на рис. 4. Как видно из графиков, при меньшем шаге система дольше выходит на установившийся режим и имеет более высокие амплитуды. Однако по результатам расчетов установлено, что временная задержка стабилизируется раньше, чем осуществляется выход на установившийся режим по амплитудам колебаний.

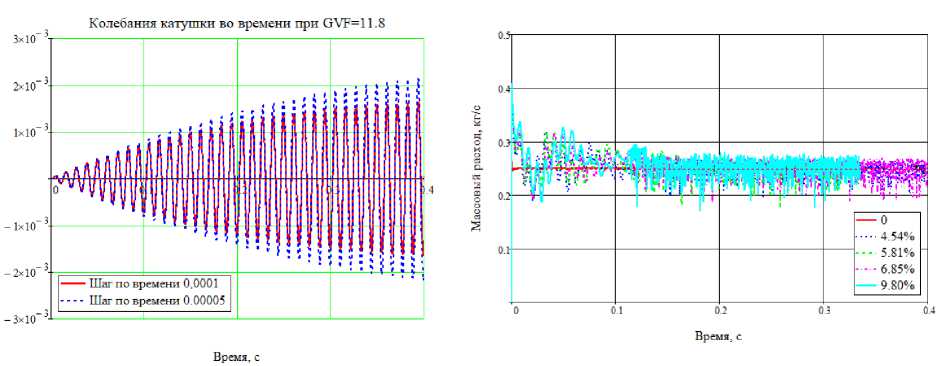
Рис. 4. Виброграммы измерительной катушки для Рис. 5. Массовые расходы жидкости в седьмом сечении двух шагов по времени в зависимости от объемной доли воздуха

С целью подтверждения закона сохранения массы, переносимой по измерительной трубке, вычислены значения массового расхода по времени через каждое из семи сечений. Так, изменение массового расхода во времени через седьмое сечение в зависимости от объемной доли воздуха в текущей среде приведено на рис. 5. При осреднении по промежутку времени значения массового расхода независимо от объемной доли воздуха в текущей среде оказались равными заданному расходу. Таким образом на имитационной модели расходомера подтверждено выполнение закона сохранения массы: масса жидкости, протекающая через каждое из семи выбранных сечений, не изменяется. При этом прямо пропорциональная массовому расходу временная задержка, которая определяется по фазам механических колебаний измерительной трубки, при наличии пузырьков воздуха в текущей среде не совпадает с временной задержкой, полученной в случае течения однородной и однофазной жидкости (рис. 6). Из анализа результатов, приведенных на рис. 6, следует, что результаты FSI расчета зависят от шага по времени, однако качественно совпадают с результатами эксперимента. И при шаге по времени 1·10–4 с, и при 5·10–5 с наблюдается качественное совпадение расчетных временных задержек с экспериментальными – снижение временной задержки с ростом объемной доли воздуха в текущей среде. При этом необходимо отметить, что расчетная модель не содержит моделей системы управления и обработки сигналов, в ней, в частности, исключены функции поддержания резонансных колебаний и фильтрации сигналов с измерительных катушек. Таким образом, по результатам расчетов и испытаний установлено, что основным источником ошибки измерения массового расхода является взаимодействие текущей двухфазной среды с деформируемой измерительной трубкой кориолисового расходоме- ра, приводящее к изменению кориолисовых сил, действующих со стороны текущей среды на измерительную трубку, и, как следствие, фаз механических колебаний узлов, соответствующих левой и правой измерительным катушкам расходомера.

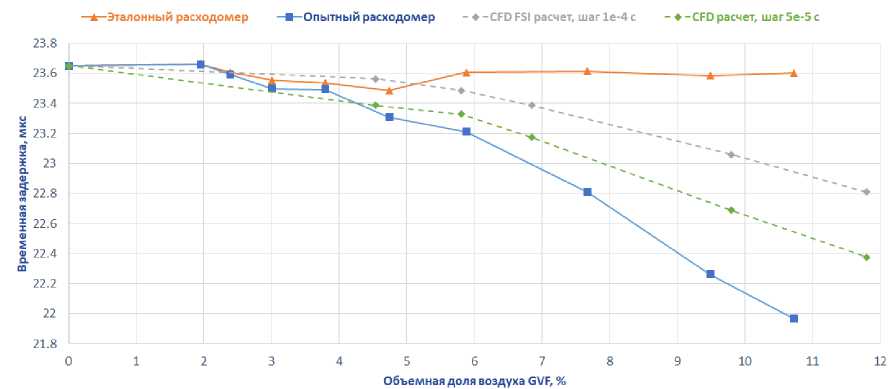
Рис. 6. Сравнение расчетных и экспериментальных временных задержек Заключение

Проведена серия экспериментальных исследований кориолисова расходомера в условиях течения двухфазной среды «жидкость–газ». В результате испытаний с ростом объемной доли воздуха в текущей среде наблюдали снижение показаний массового расходомера на опытном расходомере при неизменных показаниях на эталонном.

Разработана численная упруго-гидродинамическая модель течения двухфазной среды «жидкость–газ» по деформируемой измерительной трубке кориолисового расходомера, и выполнена серия расчетов при фиксированном расходе жидкости и различном объемном содержании воздуха в текущей среде. По результатам FSI расчетов установлено, что колебания расхода жидкости (и смеси) в выбранных произвольно семи сечениях трубки не зависят от объемной доли воздуха.

По результатам численного моделирования установлено, что при увеличении объемной доли воздуха в текущей двухфазной среде «вода–воздух» и постоянном расходе жидкости растет ошибка измерения в сторону уменьшения показаний расхода. Получено качественное совпадение результатов численного моделирования и эксперимента. По результатам численного моделирования исключено влияние алгоритмов управления и обработки сигналов на определение временной задержки.

Исследование выполнено за счет гранта Российского научного фонда № 23-29-10151,