Исследование влияния формы колосника на отделение сора от летучки

В хлопкоочистительной промышленности для очистки хлопка-сырца от крупных сорных примесей применяют пильчато-барабанные очистители [1]. Регламентированный технологический процесс первичной обработки хлопка предусматривает комплекс очистительного оборудования, обеспечивающего в заданных нормах выход продукта на хлопкозаводах.

Весьма важным фактором эффективности очистки является способ воздействия рабочих органов очистителей на хлопок-сырец [2, 3]. Результаты воздействия рабочих органов очистителей, в свою очередь, зависят от ряда факторов: производительности очистителей, частоты вращения рабочих органов, конструкции рабочих органов, повторности очистки и других показателей очистителя [4].

Одной из важнейших проблем отрасли является исследование и совершенствование конструкций очистителей хлопка-сырца от крупных и мелких сорных примесей. Повреждаемость волокна и семян с образованием сопутствующих пороков в волокне всегда ставит исследователей процесса перед трудной проблемой повышения интенсивности очистки с одновременным сохранением природных свойств материала [5, 6].

Решение этих вопросов даст возможность найти оптимальную конструкцию механизмов очистки хлопка-сырца, что приведет к повышению эффекта очистки хлопка-сырца от сорных примесей.

Объекты и методы исследования

Объектом исследования является секция «пильчатый барабан - колосниковая решетка» очистителей крупного сора. В пильчатых очистителях хлопка-сырца от крупного сора на изменение очистительного эффекта пильчатой секции наряду с другими параметрами оказывает большое влияние форма поперечного сечения колосника (конфигураций эпициклоидов) [7]. Для определения влияния формы поперечного сечения колосника на процесс отделения сора от летучки хлопка-сырца рассмотрим взаимодействие засоренной летучки и колосника в момент их контакта.

В процессе очистки в течение времени удара (порядка 0,0021 с) летучка находится в контакте с колосником и при этом огибает колосник.

На рисунке показана схема для определения сил натяжения летучки при огибании колосника засоренной летучкой, где 1– колосник с принудительным вращением, 2 – крупный сор, 3 – летуч-

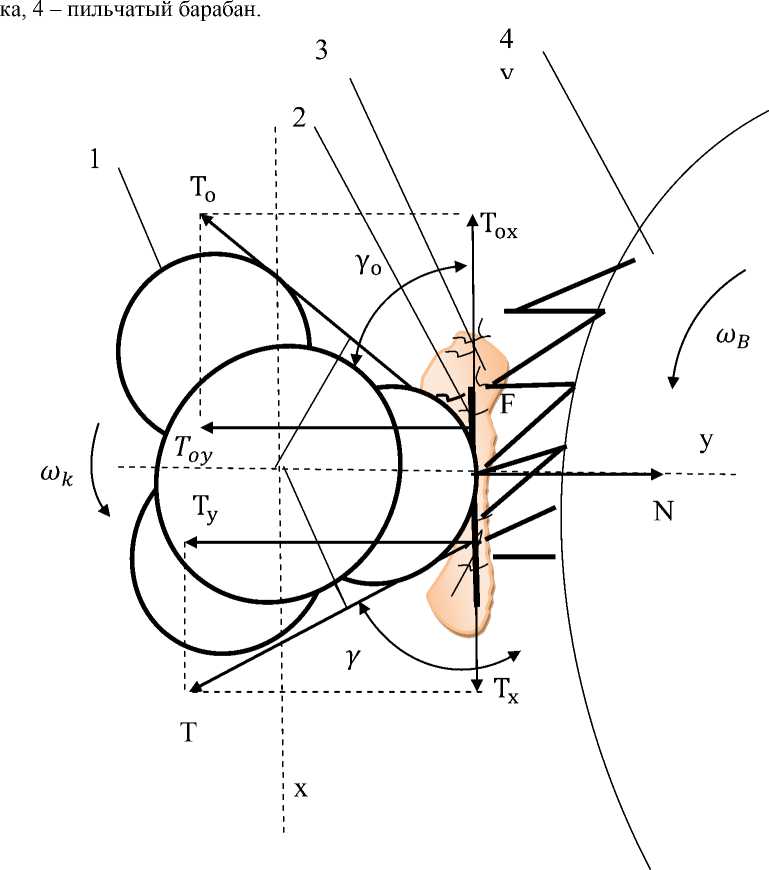
Схема для определения сил натяжения летучки при огибании колосника засоренной летучкой

Летучка перемещается по поверхности колосника на определенное расстояние (примерно 11,55 mm при скорости пильчатого барабана 7 m/с), которое зависит от скорости вращения пильчатого барабана, так как волоконца летучки захвачены зубьями пилок вращающегося пильчатого барабана. При перемещении летучки с сорными примесями удлиненной формы по колоснику с некоторой относительной скоростью V отн на сорную примесь, связанную с волокнистой массой, действуют силы натяжения в сбегающей (Т) и набегающей ветвях (Т _о ), силы трения и реакции колосника [8–11].

Для упрощения анализа предположим, что углы отрыва в обеих ветвях летучки равны между собой, т.е. γ = γо. Горизонтальные составляющие сил натяжения в этом случае определяются по формуле

T_ox=T₀ cos y, T_x=T cos y, (1)

а вертикальные – по формуле

T_oy=T_o sin y,          T_y=T sin y.

Горизонтальная сила натяжения летучки Тх создает необходимое усилие для перемещения по колоснику летучки с находящимся на ней сором. Под действием вертикальных составляющих происходит отделение сора от волокнистой массы летучки. Чем больше величина вертикальной составляющей сил натяжения, тем лучше условия для отделения крупных сорных примесей от летучек. Как видно из выражений (1) и (2), величина сил отрыва ( , ) сорных примесей от летучек зависит от угла отрыва и величины сил натяжения в сбегающей и набегающей ветвях летучки [12, 13].

Углы отрыва, в свою очередь, зависят от диаметра колосника и его поперечного сечения. Поскольку при постоянных размерах летучки угол обхвата летучкой колосников различных диаметров и поперечных сечений будет различным, для определения сил натяжения в набегающей и сбегающей ветвях летучки в зависимости от угла обхвата и скорости движения летучки необходимо рассмотреть процесс движения ее по колоснику [14–16].

Условно принимаем летучку за гибкую нить с постоянным поперечным сечением, имеющую определенную массу и скорость движения по шероховатой поверхности. Кроме этого, допускаем, что на летучку по длине действует непрерывное усилие и летучка является нерастяжимой. Рассмотрим условия равновесия летучки как гибкой нити на криволинейной поверхности, уравнение которой описывается в виде f (x , у, z). (3)

Тогда возможное перемещение летучки не является произвольным, а будет выражено следующей зависимостью:

(grad f,dr) = — 5 x + — S y + — 5 z = 0. (4) S x d y d z

Число этих условий будет соответствовать числу элементов летучки, а пока будем считать поверхность абсолютно гладкой и связь идеальной. Для составления уравнения равновесия выражение (4) умножим на и возьмем их суммарное выражение для всех элементов.

d f _ d f _s af _s

— Sx +-- S y +-- S z ) dS a y      d y      a z

J ( / /grad f, dr) ds = J u ( AB                AB

Этот интеграл сложим с выражением элементарной работы приложенной внешней силы и сил натяжения, тогда получим

S A + J Q 2 ddS ) dS - J A dS + J u ( u grad f, dr) ds = 0.                                    (6)

AB          AB       AB

Раздельно проинтегрируем J ASdS и произведем соответствующие подстановки. Коэффици- енты вариации приравняем к нулю, тогда можно получить уравнение равновесия летучки на криволинейной поверхности d (Tl °) + Q 2 + Mgradf = 0 dS

В этом уравнении выражение        – это реакция поверхности, приходящаяся на единицу длины летучки

N = u grad f

Тогда в проекции на оси x, y, z выражение (7) можно представить в виде

—(Tdx ) + Q2x dS   dS     2 x	+ N x
d- (Tdy ) + Q^ dS   dS    2 y	+ N y
d- (Tdz ) + q2z dS   dS     2 z	+ N z

= ° ,

= ° , = ° .

Уравнение равновесия (8) спроецируем на оси, выбранные следующим образом. Единичный вектор касательной к линии, составленной нитью на криволинейной поверхности, обозначим τ0, а к главной нормали – , при этом положительную нормаль поверхности обозначим Oυ. Направим перпендикулярно нормали и касательной Oυ ось Oj таким образом, чтобы она составила правую систему координат. Единичные векторы выбранной системы координатных осей обозначим τ0 и

. Тогда уравнение (8) можно записать в виде dT    T

• — T 0 + — n 0 + Q 2 + pgradf = 0.

dS   p

Проекции на выбранные оси O_r, O j _, O_υ будут иметь вид

— + Q2r = 0, dS 2T

T

• -    (n 0, J 0) + Q 2 j = 0 ,

p

T

• —    (v0 , n0 ) + Q2v + Pgradf = 0 . p

Радиус кривизны поверхности обозначим ρυ, тогда v0,n0 _  1

.

P Pv

С учетом выражения (11) формулу (12) можно написать в следующем виде:

• —    + Q^ = 0 ,

dS 2T

T _

• — + Q 2j= 0,

P j

T

---+ Q 2v + Pgradf = 0.

Pv

Уравнение равновесия летучки на колоснике с учетом сил трения будет иметь вид

d — 0 ) dS

+ Q2 + pgradf - kp / grad / t0 = 0 .

Как упомянуто выше, летучка движется по поверхности колосника со скоростью Vотн . Если летучка будет двигаться по вращающемуся колоснику, относительная скорость ее будет состоять из двух скоростей: скорости барабана (так как летучка захвачена зубом барабана) и скорости колосника [17–19]. В зависимости от направления вращения колосника относительная скорость летучки может возрастать (направление вращения барабана и колосника совпадают) или уменьшаться, что может быть выражено

^omH.= V6 ± Vk, (15)

где _б – скорость пильчатого барабана, м/с; _к – скорость колосника, м/с.

С учетом массы и скорости летучки формулу (11) можно написать

— - q sin ф - kN = 0,      — - q cos ф - N = qVomH ,                          (16)

dS                   P            gp где q - масса летучки на единицу длины, Н/м; к - коэффициент трения; q Vo2mH ]gP - сила инер- ции, Н; – угол обхвата, рад.

Сократим оба уравнения на N и с учетом того, что d S = ρd , напишем

— - k— = q P (sin ф - k cos ф ) + q о^⁰™ d ф                     g P

Проинтегрировав и проведя соответствующие математические действия, получим уравнение для определения Т :

T = Toek + qr

1 - k2

1 + k2

(( e - f

2k

- cos ф)--- sin ф

1 - k

+ m(Уб ±v, )2 (ek -1) r

где Т и Т 0 – сила натяжения в сбегающей и набегающей ветвях, N; k – коэффициент трения летучки по колоснику ( k = 0,37); r – радиус колосника, м; m – масса летучки, кг.

В равенстве (18) для рассматриваемого случая переменными являются угол обхвата колосника летучкой и относительная скорость движения летучки по колоснику.

Угол обхвата колосника летучкой зависит от формы и размеров поперечного сечения колосника [20].

Результаты и их обсуждения

Углы обхвата определены на основании тригонометрических расчетов при условии, что размеры летучки постоянные.

Рассчитанные углы обхвата в зависимости от формы поперечного сечения при диаметре описанной окружности колосника 15, 20, 25, 30, 35 и 40 мм соответственно составляют 2,7; 2,1; 1,72; 1,44; 1,21; 1,05 рад. при трехгранной форме; 2,7; 2,05; 1,64; 1,38; 1,19; 1,04 рад. – при шестигранной и 2,67; 2,0; 1,6; 1,33; 1,16 и 1,0 рад. – при круглой.

Зная значения углов обхвата в зависимости от формы поперечного сечения, диаметра и скорости вращения колосника, по выражению (18) определим значения сил натяжения летучки (табл. 1).

Значения сил натяжения летучки

Таблица 1

Форма поперечного сечения колосника	Частота вращения колосника, с –1	Сила натяжения летучки N при диаметре колосника, м
		15	20	25	30	35	40
	8,33	3,12	1,70	1,16	0,91	0,73	0,56
	16,66	3,46	1,94	1,34	1,08	0,88	0,81
Трехгранная	25	33,,4862	2,29	1,56	11,,0288	1,07	00,,8917
	33,33	4,19	2,46	1,79	1,47	1,25	1,14
	8,33	3,07	1,66	1,08	0,88	0,72	0,65
	16,66	3,40	1,89	1,26	1,04	0,87	0,80
Шестигранная	25	3,75	2,14	1,46	1,23	1,05	0,96
	33,33	4,12	2,40	1,68	1,42	1,23	1,13
	8,33	2,96	1,60	1,06	0,84	0,71	0,64
Круглая	16,66	3,27	1,81	1,24	1,0	0,85	0,79
	25	3,61	2,07	1,43	1,18	1,04	0,94
	33,33	3,96	2,32	1,64	1,36	1,22	1,11

Зная величину силы натяжения летучки из выражения (2), определим значение сил отрыва волокон летучки от сорных примесей, находящихся на летучке (табл. 2).

Из приведенных данных видно, что с увеличением диаметра описанной окружности поперечного сечения колосника сила отрыва волокон летучки от сорных примесей падает.

Заключение

• 1.    Выявлено, что угол обхвата колосника летучкой зависит от формы и размеров поперечного сечения колосника.

• 2.    Величина силы отрыва сора от летучки (τ y ) зависит также от частоты вращения и формы поперечного сечения, а максимальная величина силы отрыва достигается при трехгранном (в рассмотренном нами случае) поперечном сечении колосника.

• 3.    Увеличение сил отрыва волоконец от сорных примесей ведет к разрушению сил сцепления между сором и летучкой, что создает благоприятные условия для повышения эффективности очистки хлопка-сырца.

Таблица 2

Значение сил отрыва волокон летучки от сорных примесей

Форма поперечного сечения колосника	Частота вращения колосника, с –1	Сила отрыва N при диаметре колосника, мм
		15	20	25	30	35	40
	8,33	3,06	1,47	0,87	0,60	0,41	0,33
	16,66	3,40	1,68	1,02	0,71	0,50	0,41
Трехгранная	25	3,75	1,90	1,18	0,84	0,61	0,49
	33,33	4,11	2,13	1,35	0,96	0,71	0,57
	8,33	3,01	1,42	0,80	0,55	0,41	0,32
	16,66	3,34	1,62	0,93	0,66	0,48	0,40
Шестигранная	25	3,68	1,83	1,07	0,78	0,59	0,48
	33,33	4,04	2,05	1,23	0,90	0,69	0,56
	8,33	2,87	1,35	0,76	0,52	0,39	0,31
Круглая	16,66	3,18	1,52	0,89	0,62	0,47	0,38
	25	3,51	1,74	1,03	0,73	0,57	0,45
	33,33	3,85	1,95	1,18	0,84	0,66	0,53