Исследование влияния концентрации лития на скорость диффузии в кристаллическом кремнии

Развитие литий-ионных аккумуляторов в настоящее время является одной из самых актуальных задач в области источников тока ввиду их перспективности, широкого использования в электронных устройствах и даже в автомобилестроении ближайшего будущего. По сравнению с другими перезаряжаемыми батареями, такими как кислотно-свинцовые, никель кадмиевые и никель-металл-гидридные, литий-йонные батареи обладают большим удельным зарядом, рабочим напряжением и меньшим током саморазряда. На сегодняшний день основным материалом анодов современных батарей является графит, который обладает адсорбционной емкостью по литию 372 мА·ч/г, а также материалы на его основе. При внедрении ионы лития слегка раздвигают слои углеродной матрицы и располагаются между ними, образуя интеркала-ты. Ввиду достаточно большого расстояния между слоями sp2-гибридизированного углерода, обеспечиваемого слабым ван-дер-ваальсовым взаимодействием, удельный объем углеродных материалов в процессе интеркаляции-деинтеркаляции ионов лития меняется незначительно, что является положительной чертой данных материалов. К сожалению, в таких материалах происходит значительный перенос электрического заряда с атомов лития на слои графита, что ведет к существенному отталкиванию ионов лития. Это приводит к тому, что максимальное содержание лития в графите соответствует фазе LiC6, соответствующей вышеупомянутой адсорбционной емкости. Однако уже известно, что теоретическая емкость для батарей с кристаллическим кремниевым анодом может составить величину в 10 раз большую, чем для углеродных материалов [1], поэтому материалы на основе кремния сейчас широко изучаются как анодный материал для следующего поколения литий-йонных батарей [2; 3]. Одним из важных аспектов исследования кремния в качестве анода является исследование диффузии лития внутри его кристаллической структуры.

В отличие от случая диффузии, в кристаллических средах с достаточно низкими потенциальными барьерами ( V barrier ~ (1÷10)·кT) для прыжков частиц, когда можно применять метод молекулярной динамики (MD), в структурах с высокими потенциальными барьерами V barrier , например в ковалентно связанных кристаллических структурах ( V barrier >> кT), частота перескоков атомов через потенциальные барьеры является чрезвычайно малой (rare events problem). Поэтому такие системы не поддаются прямому исследованию методом MD. Для ускорения моделирования процессов активационных перескоков в таких случаях были разработаны методики смещающего потенциала (bias potential) [4], метод гипердинамики [5], а также метод температурно-ускоренной динамики (temperature-accelerated dynamics) [6]. К сожалению, применение данных методик для реальных систем сдерживается сложностью интегрирования данных методик в стандартные MD алгоритмы и сложностью определения потенциального профиля для движения диффунди-руемых частиц. Особенно это касается описания диффузии в аморфных веществах, когда имеется бесконечное многообразие потенциальных профилей и барьеров для диффузии частиц.

Целью данной работы являлась разработка метода расчета диффузии примеси на основе данных, полученных из квантово-химических расчетов, и применение данного метода для исследования влияния концентрации атомов лития на скорость его диффузии.

Квантово-химические расчеты в работе проводились в рамках метода функционала плотности (DFT) [7] с градиентными поправками Perdew-Burke-Ernzerhof (PBE) [8] с коррекцией Grimme, учитывающей ванн-дер-ваальсово взаимодействие [9] в лицензионном пакете VASP (Vienna Ab-initio Simulation Package) [10–13]. Для эффективного уменьшения количества базисных функций и увеличения скорости расчетов в программе для всех атомов использовались псевдопотенциалы Вандербильта (Vanderbilt ultrasoft pseudopotential) [14]. Для выбора оптимальных параметров расчета и точности интегрирования по первой зоне Бриллюэна был использован набор к-точек, сгенерированный с помощью метода Монхорста-Пака [15] на равномерной сетке 3X3X3, так как было обнаружено, что благодаря большому размеру суперячейки увеличение числа к-точек не приводит к изменению энергии связи и электронной структуры, но значительно увеличивает время расчетов. Для проведения оптимизации геометрии координаты всех атомов в суперячейках варьировались с помощью метода сопряженных градиентов, используя вычисление сил, действующих на атомы. При этом оптимизация проводилась до тех пор, пока силы, действующие на каждый атом, не становились менее 0,05 эВ/Å.

Для расчетов была использована суперячейка кремния в виде куба, состоящая из 216 атомов. Кремний имеет алмазоподобную кристаллическую структуру, в которой атомы лития могут располагаться в тетраэдрических порах данной структуры, максимальное число таких пор, в которых могут находиться атомы лития, равно числу атомов кремния. В данную ячейку помещали от одного до четырех атомов лития, причем их расположение выбиралось таким образом, чтобы расстояние между ними было минимальным, и проводили оптимизацию геометрии. После этого один из атомов лития помещали в соседнюю к нему пустую пору (в ячейках, где больше двух литиев, изменяли положение лития, равноудаленного от других) и оптимизировали полученную ячейку. Далее была рассчитана высота потенциального барьера (переходное состояние) для прыжков атома лития между двумя оптимизированными состояниями. Данные расчеты были выполнены методом эластичной упругой ленты (NEB) [16]. При этом были рассчитаны траектория, потенциальный профиль и величина барьера перехода атома лития через седловую точку потенциального профиля. Высота потенциальных барьеров перескока атома лития с различным заполнением окружения представлены в таблице.

Высота потенциального барьера перескока атома лития в зависимости от количества атомов лития в ячейке LixSi216

Количество атомов Li	1	2	3	4
Высота барьера, эВ	0,903	0,749	0,477	0,362

Полученные данные были использованы для получения полиноминальной зависимости высоты барьера перескока атома лития от степени заполнения соседних к нему пор такими же атомами:

V barrier = A E ь о - 0,07 P 3 + 0,277 P ² - 0,375 P , (1)

где A E b ₀ = 0,903 эВ (рассчитанное значение высоты барьера перескока атома лития из одной тетраэдрической поры в соседнюю без окружающих атомов лития).

Сумма вероятностей заполнения атомами лития пор окружающих ячейку, из которой совершается перескок, за исключением той, в которую совершается перескок ( m = 1,2,3), составляет

P = Z P m .                  (2)

Для вычисления коэффициента диффузии была предложена эффективная методика, основанная на вычислении временной эволюции распределения атомов лития P ( R i , t n ) в дискретном времени t n и пространстве R i . Данная эволюция описывается дискретным (заменяющим непрерывное уравнение диффузии) производящим уравнением (master equation) марковского процесса для степени заполнения узла i в момент времени t k :

D dP(Ri, tn ) _ X 1 Hi D D \Di D * МЛ Di D * \\

----”----= A W (Ri, Rj ) P(Rj , tn )(1 - P (Ri, tn )) - dt       Rj                                         (3)

D         D              D                                D

- W(Rj,Ri)P(Ri,tn)(1 -P(Rj,tn)), здесь W(Ri,Rj) – частота перескока атома примеси из минимума R j в минимум Ri . Данные величины для прыжка атома в любом направлении Ri ^ Rj через барьер Vbarrier(Ri, Rj) при температуре T рассчитывались с помощью уравнения аррениусовского типа:

W (R i , Rj ) = W 0 exp ^f- V ^{barrier (} R i , R^j) 1 .       (4)

I kT J

Предэкспоненциальный множитель (эффективная частота колебаний) W 0 вычислялся с помощью известной формулы Веньярда [17], также учитывающего энергию нулевых колебаний E 0 :

W 0 =

3 N - 3 f     - ^{h v} i

П 1 - e ^kT kT i = 1 |          _?

Й 3 N - 4 f       ^{h v} i

П 1 - e^kT i = 1

где v ‘ - частота колебаний N атомов системы при нахождении перемещаемого атома в седловой точке, а ν _i – в точке минимума.

После 100 итераций расчет распределения вероятности нахождения атомов лития в каждом из узлов выполнялся расчет коэффициента диффузии. Для этого численно решалось основное уравнение диффузии:

dc дx ’

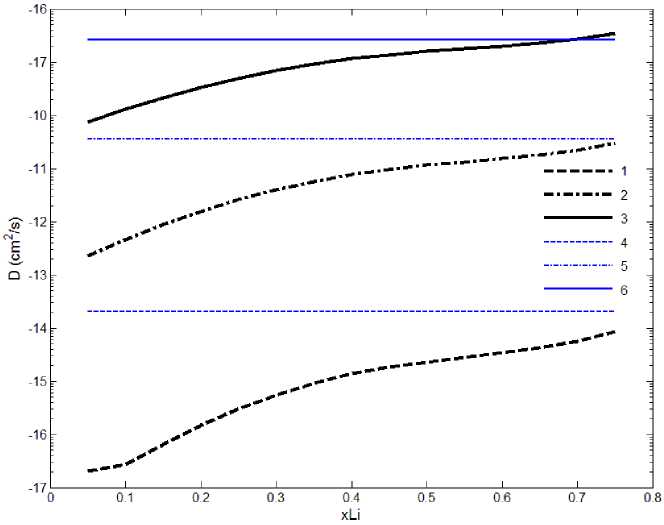
Зависимость коэффициента диффузии от концентрации лития в структуре LixSi:

при температуре: 1 – 273 К; 2 – 373 К; 3 – 473 К; экспериментальные данные: 4 – 273 К; 5 – 373 К; 6 – 473 К

здесь поток J – результирующее число атомов лития, прошедших в единицу времени через единичную площадь плоскости, перпендикулярной оси, вдоль которой направлен с – градиент концентрации атомов лития в этой плоскости (в числах атомов на единицу объема). Графики температурной зависимости коэффициентов диффузии с различной начальной концентрацией лития представлены на рисунке линиями с номерами 1, 2,3 для температуры 273, 373 и 473 К соответственно.

Линиями 4, 5, 6 показаны коэффициенты диффузии для аналогичных температур полученные из экспериментальной зависимости [18, 19]:

D = 2,5 ■ 10 - 3 ■ exp ^f2 0,^551211 ( k ■ T

В отличие от работы [20], в которой рассматривалась зависимость коэффициента диффузии от температуры, представленный алгоритм расчета позволил определить зависимость коэффициента диффузии как от температуры, так и от концентрации лития.

Итак, в ходе выполнения работы с помощью проведения первопринципных расчетов была получена зависимость коэффициента диффузии от концентрации лития и температуры в кристаллическом кремнии. Обнаружено значительное (на 1–2 порядка) увеличение скорости диффузии лития в кремнии при увеличении концентрации лития до состава Li 0,75 Si.

Referens

• 1.    Kasavajjula U., Wang C. S., Appleby A. J. Nano-and bulk-silicon-based insertion anodes for lithium-ion secondary cells. J. Power Sources. 2007, vol. 163, 1003 p.

• 2.    Winter M., Besenhard J. O. Electrochemical lithia-tion of tin and tin-based intermetallics and composites. Electrochim. Acta, 1999, vol. 45, 31 p.

• 3.    Huggins R. A., Lithium alloy negative electrodes. J. Power Sources . 1999, vol. 81–82, 13 p.

• 4.    Hamelberg D., Mongan J., McCammon J. A. Accelerated molecular dynamics: A promising and efficient simulation method for biomolecules. J. Chem. Phys . 2004, vol. 120, 11919 p.

• 5.    Voter A. F. Hyperdynamics: Accelerated Molecular Dynamics of Infrequent Events. Phys. Rev. Lett. 1997, vol. 78, 3908 p.

• 6.    Sorensen M. R., Voter A. F. Temperature-accelerated dynamics for simulation of infrequent event. J. Chem. Phys . 2000, vol. 112, 9599 p.

• 7.    Kohn W., Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, vol. 140, 1133 p.

• 8.    Perdew J. P., Burke K., Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, vol. 77, pp. 3865–3868.

• 9.    Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comp. Chem. 2006, vol. 27, 1787 p.

• 10.    Kresse G., Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B. 1993, vol. 47, № 1, pp. 558–561.

• 11.    Kresse G., Hafner J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B. 1994, vol. 49, № 20, pp. 14251– 4269.

• 12.    Kresse G., Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Computer Material Science. 1996, № 6, 15 p.

• 13.    Kresse G., Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B. 1996, vol. 54, 11169 p.

• 14.    Vanderbilt D. Soft self-consistent pseudopotentials in generalized eigenvalue formalism. Phys.Rev. B. 1990, vol. 41, 7892 p.

• 15.    Monkhorst H. J., Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B. 1976, vol. 13, pp. 5188–5192.

• 16.    Henkelman G., Jonsson H. Improved tangent estimate in the nudged elastic band method for finding

  minimum energy paths and saddle points. J. Chem. Phys . 2000, vol. 113, pp. 9978–9985.

• 17.    Vineyard G. V. Frequency factors and isotope effects in solid state rate processes. J. Phys. Chem. Solids. 1957, vol. 3, pp. 121–127.

• 18.    Pell E. M. Diffusion of Li in Si at High T and the Isotope Effect. Phys. Rev . 1960, vol. 119, № 3, pp. 1014–1021.

• 19.    Pell E. M. Diffusion Rate of Li in Si at Low Temperature. Phys. Rev. 1960, vol. 119, № 4, pp. 1222–1225.

• 20.    Fedorov, A. S., Popov Z. I., Kuzubov A. A., Ovchinnikov S. G. Teoreticheskiye issledovaniye diffuzii litiya v kristallicheskom i amorfnom kremnii (Theoretical study of lithium diffusion in crystalline and amorphous silicon). Pis'ma v ZHETF . 2012, vol. 95, pp. 159–163.