Исследование влияния массовой производительности на качество работы центробежного сепаратора продуктов биоконверсии

Введение. Одним из приоритетных направлений развития агропромышленного комплекса является создание нового и усовершенствование существующего технологического оборудования и технологий биоконверсии. Очистка выращенной биомассы от сопутствующих материалов является одной из основных технологических операций получения готового продукта. Поэтому разработка сепаратора продуктов биоконверсии является актуальной задачей. Волокнистое строение выращенной биомассы является положительным фактором для применения центробежного сепаратора. Центробежные сепараторы имеют простую надежную конструкцию, позволяющую технологи- чески и экономически эффективно извлекать частицы твердой фракции из жидкости в поле центробежных сил [1, 2]. Одним из перспективных направлений повышения эффективности центробежных сепараторов является исследование дисперсного потока. Поведение дисперсного потока в сепараторах определяется множеством конструктивных и технологических параметров. На основании анализа работ [3–6], были приняты следующие параметры, характеризующие качество потока: траектория движения частицы жидкости; осевая мгновенная скорость частицы жидкости в рабочей камере vоiчж в м/с; радиальная мгновенная скорость частицы жидкости в рабочей камере vriчж в м/с; тан- генциальная мгновенная скорость частицы жидкости в рабочей камере vτiчж в м/с.

В качестве фактора, способного оказывать влияние на качество дисперсного потока, было выбрано изменение производительности центробежного сепаратора.

Материал и методика исследования. Для исследования гидродинамики по- тока в качестве модели технологического материала была использована лагранжева модель Discrete Phase Model (модель дискретной фазы DPM) с использованием математической модели на основе системы уравнений Навье-Стокса, осредненной по Рейнольдсу, которая имеет вид [8, 9, 10, 11]:

^ = 0

_ d X i

+ dt   dXj

(U i U ₇ ) =

1 dp 1 d , du. --— +-- ( p —^L p dx.  p dXj d x.

^, pv¹

где индексы i =1, 2, 3, j = 1, 2, 3 определяют направления цилиндрической системы координат; x i ; u i , u j u k – составляющие скорости; p - плотность жидкости; ц - коэффициент динамической вязкости жидкости; p – давление; t – время.

При моделировании турбулентности применена модель напряжений Рейнольдса, для вычисления каждой из компонент тензора τ ij c учетом его симметрии решаются шесть уравнений переноса, получающиеся из исходных уравнений Навье-Стокса (1) [7, 8, 9, 10] с помощью операции осреднения:

'        '                                                 ''

duu —duu.

---j + uk---j =-- d t        dxk

'   '  ' I ¹ /   '   ' e .     '   ' X A         ^{d uiu} j

+

ukuiuj + - (P uj5jk + P ujSk ) - V -- p                     dXk

+

—г-T d uj uiuk dXk

~r~r dui

uu j k dXk

+

P ' ^{d u} i

d u

-

p I dX

d X

2v

d u. d u

d X_k d X_ki

где ν – коэффициент кинематической вязкости;

• 5 -    символ Кронекера.

Моделирование проводилось на предложенной модели сепаратора (рисунок 1) с помощью пакета ANSYS Fluent. В качестве области расчета использовалось внутреннее пространство сепаратора, условия пред- ставлены в таблице 1. Расчет проводился при заданных значениях массовой производительности 2,5, 5, 10 кг/ч.

Построение геометрической модели проводилось в трёхмерном проектировании КОМПАС-3D с импортированием в Design Modeler.

Таблица 1 – Условия исследования Table 1 – Study conditions

Плотность жидкости p, кг/м3 Liquid density p, kg/m3	998
Коэффициент динамической вязкости жидкости ц, Па - с Coefficient of dynamic liquid viscosity ц, Pa - s	0,001
Внутренний диаметр рабочей камеры Dвну рк , мм Inner diameter of working chamber Dinner wch , mm	150
Внутренний радиус входного патрубка rвну вх.п , мм Inner radius of inlet pipe rinner inl p , mm	15

Для выделения решения из общего множества дифференциальных уравнений, описывающих движение среды, необходимо задать переменные на границах расчетной области модели. В предлагаемой модели сепаратора на входных границах была принята цилиндрическая система координат, у которой задаются три компоненты для описания направления модуля средней скорости. Стенки модели жесткие, неподвижные, внутренние поверхности гладкие с условием прилипания, постоянной, равномерной, зернистой шероховатостью, величина которой 0,5 мкм. Данные параметры выбраны так, чтобы при использовании модели рейноль-дсовых напряжений турбулентности сопротивление трубы соответствовало данным графика Никурадзе [11]. На выходных гра- ницах заданы параметры возвратного потока, который может возникнуть при втекании потока через границу. Направления возвратного потока задаются при помощи нормали к границе потока. Для этого достаточно задать интенсивность турбулентности и отношение турбулентной вязкости (таблица 2).

Интенсивность турбулентности I для полностью развитого турбулентного течения в трубе определяется из следующей эмпирической зависимости:

I =0,16⋅Re-1/8 dh , где Redh – число Рейнольдса, рассчитанное по гидравлическому диаметру.

Подставив значения, получили I =2%, что соответствует течению со средней турбулентностью.

Таблица 2 – Зависимость отношения турбулентной вязкости β от Re Table 2 – Dependence of turbulent viscosity relations β on Re

Re	3000	5000	10000	15000	20000	>100000
β	11,5	16,5	26,7	34,0	50,1	100

Скорость v чж , м/с Velocity v lp, m/s

7.62

6.85

6.09

5.33

4.57

3.81

3.05

2.28

1.52

0.76

ООО

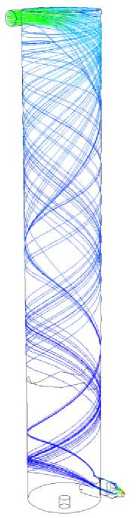
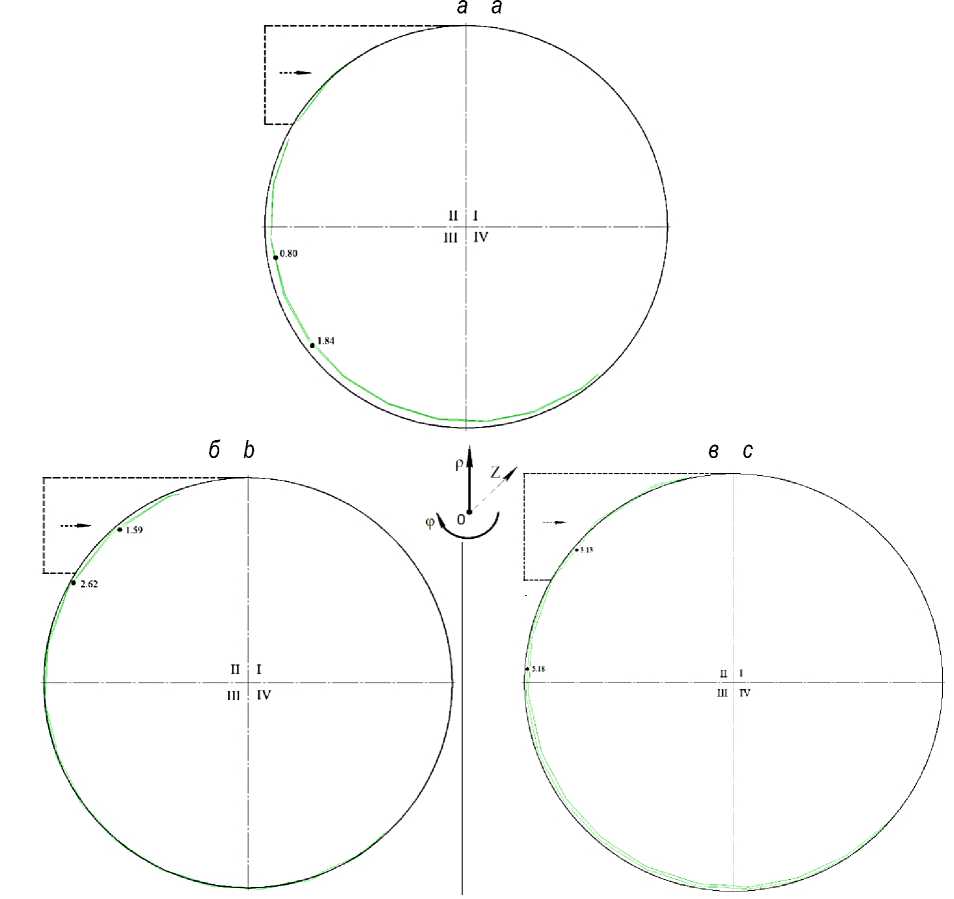
Рисунок 1 – Схемы траекторий движения частиц жидкости при массовой производительности 2,5 кг/с

Figure 1 – Schemes of trajectories of liquid particles at mass productivity 2,5 kg/s

Результаты исследований. Выполним анализ результатов экспериментов. Рассмотрим случай, когда массовая производительность составляет 2,5 кг/с.

Анализ результатов экспериментов по схемам траекторий движения твёрдых частиц (рисунок 1) показал, что имеет место плавный переходный в пространстве и стационарный во времени режим потока частиц жидкости; дополнительные завихрения не наблюдаются.

Рассмотрим случай, когда массовая производительность составляет 5 кг/с. Анализ результатов экспериментов по схемам траекторий движения частиц жидкости (рисунок 2) показал, что имеет место плавный переходный в пространстве и стационарный во времени режим потока частиц жидкости; дополнительные завихрения не наблюдаются.

Скорость v чж , м/с

Velocity v lp, m/s

15 24

13.71

12.19

10.67

9.14

7.62

6 09

4.57

3.05

1.52

0.00

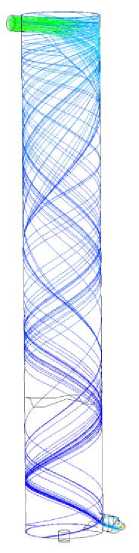
Рисунок 2 – Схемы траекторий движения частиц жидкости при массовой производительности 5 кг/с

Figure 2 – Schemes of trajectories of liquid particles at mass productivity 5 kg/s

Рассмотрим случай, когда массовая производительность составляет 10 кг/с. Анализ результатов экспериментов по схемам траекторий движения частиц жидкости (рисунок 3) показал, что имеет место плавный переходный в пространстве и стационарный во времени режим потока частиц жидкости; дополнительные завихрения не наблюдаются.

Анализ результатов экспериментов по схемам контуров изолиний скоростей движения частиц жидкости выполним для трёх составляющих скорости (осевой, радиальной и тангенциальной), в сечении рабочей камеры на расстоянии 10 r от входного торца рабочей камеры, где r – радиус входного патрубка.

Рассмотрим осевую составляющую скорости (рисунок 4).

Скорость v чж , м/с Velocity v lp, m/s

30 33

27 30

24 26

21.23

18 20

15 16

12 13

6.07

3.03

0.00

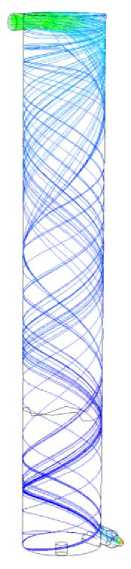
Рисунок 3 – Схемы траекторий движения частиц жидкости при массовой производительности 10 кг/с

Figure 3 – Schemes of trajectories of liquid particles at mass productivity 10 kg/s

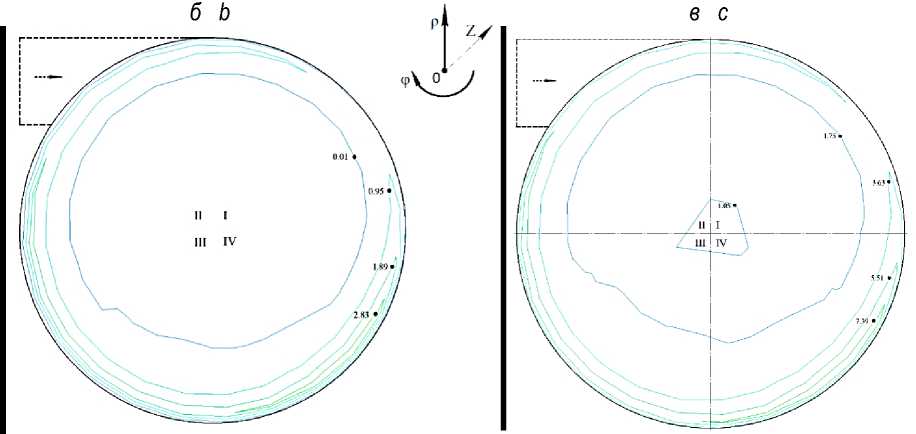
В рассматриваемых радиальных сечениях рабочей камеры наблюдаются различия в численных значениях осевых составляющих скоростей движения твердых частиц.

На рисунке 4 а максимальное значение v^о max = 1,89 м/с осевая составляющая скорости имеет на периферии рабочей камеры в IV квадранте. Знак минус объясняется тем, что в принятой цилиндрической системе координат главная продольная ось рабочей камеры направлена от входного торца рабочей камеры к выходному. Минимальное значение по абсолютной величине осевой составляющей скорости имеет v^о min = 0 м/с.

На рисунке 4 б максимальное значение v^о max = 2,81 м/с осевая составляющая скорости имеет на периферии рабочей камеры в IV квадранте, а минимальное v^о min = 0,01 м/с в её центральной зоне.

На рисунке 4 в максимальное значение v^о max = 7,39 м/с осевая составляющая скорости имеет на периферии рабочей камеры в IV квадранте, а минимальное v^о min = 1,05 м/с в её центральной зоне. При этом наблюдается следующая закономерность: большие значения осевой составляющей скорости возникают на периферии рабочей камеры, а меньшие – в её центре, при этом повышенные значения осевой составляющей скорости в рассматриваемых сечениях смещаются по направлению вращательного движения потока. Это говорит о струйном характере потока. Дополнительные завихрения, кроме основного вращения потока вокруг главной продольной оси рабочей камеры, в радиальной плоскости не наблюдаются. Но присутствуют завихрения в продольной плоскости рабочей камеры на рисунке 4 а .

а a

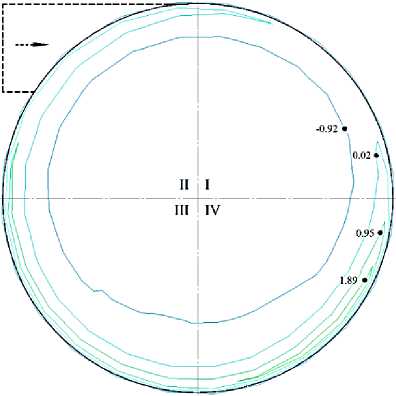
а – массовая производительность 2,5 кг/с; б – массовая производительность 5 кг/с;

в – массовая производительность 10 кг/с

Рисунок 4 – Схемы контуров изолиний осевых скоростей движения твердых частиц в радиальных сечениях рабочей камеры а – mass productivity 2,5 kg/s; b – mass productivity 5 kg/s; c – mass productivity 10 kg/s Figure 4 – Flow charts of isolines of axial velocities of solid particles in the radial sections of the working chamber

Рассмотрим радиальную составляющую скорости (рисунок 5).

В рассматриваемых радиальных сечениях рабочей камеры наблюдаются разли- чия в численных значениях радиальных составляющих скоростей движения твердых частиц.

а – массовая производительность 2,5 кг/с; б – массовая производительность 5 кг/с;

в – массовая производительность 10 кг/с

Рисунок 5 – Схемы контуров изолиний радиальных скоростей движения твёрдых частиц в радиальных сечениях рабочей камеры

а – mass productivity 2,5 kg/s; b – mass productivity 5 kg/s; c – mass productivity 10 kg/s Figure 5 – Flow charts of isolines of radial velocities of solid particles in the radial sections of the working chamber

На рисунке 5 а максимальное значение v^r max = 1,84 м/с радиальная составляющая скорости имеет в пространстве во II и в III квадрантах. Минимальное значение v^r min = 0,80 м/с радиальная составляющая скорости имеет, начиная с периферии II и III квадрантов до стенок рабочей камеры I и IV квадрантов.

На рисунке 5 б максимальное значение v^r max = 2,62 м/с радиальная составляющая скорости имеет на периферии рабочей камеры во II и в III квадрантах, а минимальное v^r min = 1,59 м/с на периферии II и III квадрантов до стенок рабочей камеры I и IV квадрантов.

На рисунке 5 в максимальное значение vrmax = 5,18 м/с радиальная составляю- щая скорости имеет также на периферии во II и в III квадрантах, а минимальное vrmin = 3,13 м/с, начиная с периферии II и III квадрантов до стенок рабочей камеры I и IV квадрантов. При этом наблюдаются следующие закономерности: повышенные значения радиальной составляющей скорости в рассматриваемых сечениях смещаются по направлению вращательного движения потока; большие значения радиальной со- ставляющей скорости возникают на периферии рабочей камеры, а меньшие – в её центре, причём разница довольно мала. Это говорит о струйном характере потока и отсутствии дополнительных, кроме основного вращения потока вокруг основной продольной оси рабочей камеры, не наблюдаются завихрения в радиальной плоскости.

Рассмотрим тангенциальную составляющую скорости (рисунок 6).

а a

б b

в c

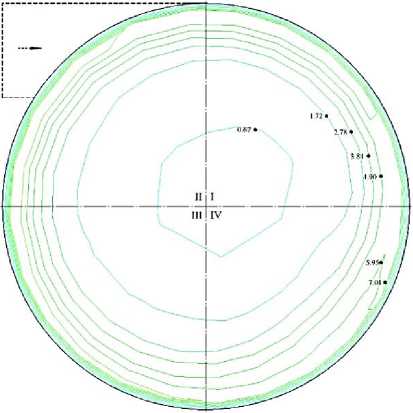
а – массовая производительность 2,5 кг/с; б – массовая производительность 5 кг/с;

в – массовая производительность 10 кг/с

Рисунок 6 – Схемы контуров изолиний тангенциальных скоростей движения твёрдых частиц в радиальных сечениях рабочей камеры а – mass productivity 2,5 kg/s; b – mass productivity 5 kg/s; c – mass productivity 10 kg/s Figure 6 – Flow charts of isolines of tangential velocities of solid particles in the radial sections of the working chamber

В рассматриваемых радиальных сечениях рабочей камеры наблюдаются различия в численных значениях тангенциальных составляющих скоростей движения твёрдых частиц.

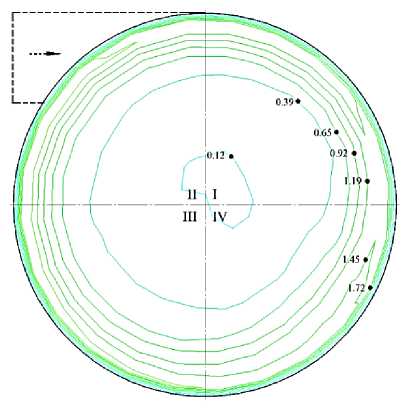
На рисунке 6 а максимальное значение v^τ max = 1,72 м/с тангенциальная составляющая скорости имеет на периферии пространства рабочей камеры, а минимальное v^τ min = 0,12 м/с в её центральной зоне.

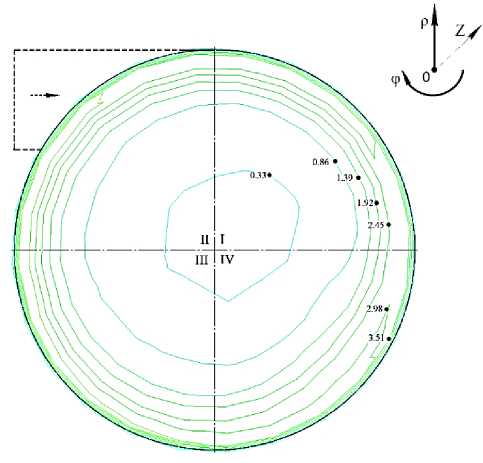
На рисунке 6 б максимальное значение v^τ max = 3,51 м/с тангенциальная составляющая скорости имеет также на периферии рабочей камеры, а минимальное v^τ min = 0,33 м/с в её центральной зоне.

На рисунке 6 в максимальное значение v^τ max = 7,61 м/с тангенциальная составляющая скорости имеет также на периферии, а минимальное v^τ min = 0,67 м/с в её центральной зоне. При этом наблюдаются следующие закономерности: повышенные значения тангенциальной составляющей скорости в рассматриваемых сечениях смещаются по направлению вращательного движения потока; большие значения тангенциальной составляющей скорости имеются на периферии рабочей камеры, а меньшие – в её центре, причём разница может составлять более 7 раз. Это говорит о струйном характере потока. Дополнительные завихрения, кроме основного вращения потока вокруг главной продольной оси рабочей камеры, в радиальной плоскости не наблюдаются. Также отсутствуют завихрения в продольной плоскости рабочей камеры.

Вывод. На основании проведённого исследования кинематики потока твёрдых частиц технологического материала центробежного сепаратора при тангенциальном расположении входного патрубка в случаях, когда массовая производительность равна 2,5; 5; 10 кг/с, можно сделать следующие выводы: независимо от массовой производительности, имеет место плавный переходный в пространстве и стационарный во времени режим потока частиц жидкости; при массовой производительности 2,5 кг/с присутствуют завихрения в продольной плоско- сти рабочей камеры, что является важным для процесса сепарации; числовые значения тангенциальных составляющих скоростей в центральной зоне рабочей камеры в зависимости от производительности меняются незначительно, тогда при массовой производительности 10 кг/с технологический материал в рабочей камере находится минимальное количество времени, что также является важным для сепарации. В связи с вышесказанным, наиболее рациональной для заданных условий исследования является массовая производительность центробежного сепаратора продуктов биоконверсии, составляющая 5 кг/с.